Реферат: Розкриття невизначеностей за правилом Лопіталя
Міністерство охорони здоров’я України
Житомирський фармацевтичний коледж
ім. Г.С. Протасевича
Реферат
на тему:
“ Розкриття невизначеностей за правилом Лопіталя”
Роботу виконала
Студентка 211 групи
Піщук Олеся
Викладач:
Виговська В.Г.
Отриманий бал:
_____________
м. Житомир – 2006
План
І. Розкриття невизначеностей з використанням правила Лопіталя.
1) Правило Лопіталя.
а) Наслідок.
б) Приклад 1.
2) Розкриття невизначеностей виду: ∞-∞; 0∙∞; 1∞; 00; ∞0.
а) Приклад 2.
б) Приклад 3.
в) Приклад 4.
Список використаної літератури.
І. Розкриття невизначеностей з використанням правила Лопіталя.
Лопіталь де Гійом Франсуа (1661-2.02.1704 рр.). Французький математик, член Парижської АН, народився в Парижі, вивчав математику під керівництвом У. Бернуллі. Видав перший друкований підручник по диференціальному обчисленню – “Аналіз нескінченно малих” (1696р.). В підручнику є правило Лопіталя – правило знаходження межі дробу, чисельник і знаменник якого прямує до 0. Крім того, він створив курс аналітичної геометрії конічних перетинів. Йому також належить дослідження і розвиток за допомогою математичного аналізу декількох важких задач по геометрії і механіці, а також одне із рівнянь знаменитої задачі о браністохроні.
1. Правило Лопіталя.
Нехай виконані умови:
1. функції f(х) та g(х) визначені і диференційовані в колі точки х0;
2.
частка
цих функцій ![]() в точці х0
має невизначеність вигляду
в точці х0
має невизначеність вигляду ![]() або
або ![]() ;
;
3.
існує ![]() .
.
Тоді існує ![]() і
виконує рівність:
і
виконує рівність:
![]() (1)
(1)
а) Наслідок.
Нехай:
1. Визначені в колі точки х0 функції f(х), g(х) та їх похідні до n-го порядку включно;
2. Частки ![]() ,
, ![]() , …,
, …, ![]() мають невизначеність
вигляду
мають невизначеність
вигляду ![]() або
або ![]() ;
;
3. Існує ![]() , тоді
, тоді
![]() (2)
(2)
б) Приклад 1.
Знайти: ![]() .
.
Розв’язання:
Функції ![]() та
та ![]() визначені з усіма своїми
похідними в околі точки х=0.
визначені з усіма своїми
похідними в околі точки х=0.
Маємо:
![]() .
.
2) Розкриття невизначеностей виду: ∞-∞; 0∙∞; 1∞; 00; ∞0.
Існують прийоми, що дозволяють зводити вказані невизначеності
до невизначеностей вигляду ![]() або
або ![]() , які можна розкривати з
використанням правила Лопіталя.
, які можна розкривати з
використанням правила Лопіталя.
1.
Нехай ![]() і
і ![]() , тоді
, тоді
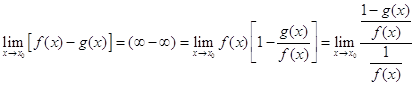 (3)
(3)
За умовою ![]() при
при ![]() , тому
, тому ![]() при
при ![]() .
.
Якщо ![]() не
прямує до 0 при
не
прямує до 0 при ![]() , то границя в
правій частині (3) не існує, а тому і границя лівої частини (3) не існує.
, то границя в
правій частині (3) не існує, а тому і границя лівої частини (3) не існує.
Якщо ![]() при
при ![]() , то вираз
, то вираз 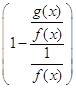 має невизначеність
має невизначеність ![]() .
.
2. Нехай ![]() ,
, ![]() , тоді
, тоді ![]() має невизначеність вигляду
має невизначеність вигляду
![]() при
при ![]() .
.
В цьому випадку поступають так:
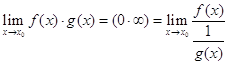
Під знаком останньої границі маємо невизначеність ![]() .
.
3. Нехай ![]() ,
, ![]() при
при ![]() . Тоді
. Тоді ![]() має невизначеність вигляду
має невизначеність вигляду
![]() .
.
Позначимо ![]() .
Шляхом логарифмування цієї рівності одержимо:
.
Шляхом логарифмування цієї рівності одержимо:
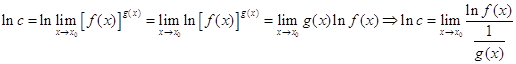
Отже, обчислення натурального логарифма границі ![]() зводиться до розкриття
невизначеності вигляду
зводиться до розкриття
невизначеності вигляду ![]() .
.
4. Невизначеності вигляду ![]() та
та
![]() зводять до
невизначеностей
зводять до
невизначеностей ![]() або
або ![]() шляхом логарифмування
аналогічно до невизначеності вигляду
шляхом логарифмування
аналогічно до невизначеності вигляду ![]() .
.
а) Приклад 2.
Знайти границю ![]() .
.
Розв’язання:
Функції ![]() та
та ![]() диференційовані, а їх
частка
диференційовані, а їх
частка ![]() має невизначеність вигляду
має невизначеність вигляду
![]() при
при ![]() .
.
Використовуючи правило Лопіталя, одержимо:
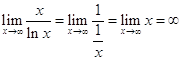 .
.
б) Приклад 3.
Знайти границю ![]() .
.
Розв’язання:
В цьому випадку маємо невизначеність вигляду ![]() . Позначимо
. Позначимо ![]() і про логарифмуємо цю
рівність. Одержимо:
і про логарифмуємо цю
рівність. Одержимо:
![]() , тобто невизначеність вигляду
, тобто невизначеність вигляду ![]() . Використовуючи правило
Лопіталя, одержимо:
. Використовуючи правило
Лопіталя, одержимо:
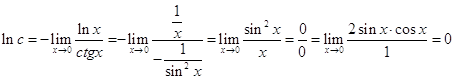 .
.
Отже, ![]() .
.
в) Приклад 4.
Знайти границю 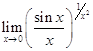 .
.
В цьому випадку маємо невизначеність вигляду ![]() . Нехай
. Нехай 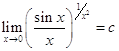 . Логарифмуючи цю рівність,
одержимо:
. Логарифмуючи цю рівність,
одержимо:
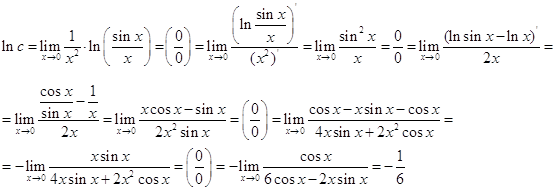 .
.
Чотири рази застосували правило Лопіталя.
Отже, маємо:
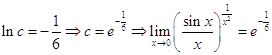
Список використаної літератури:
1. Кривуца В.Г., Барковський В.В., Барковська Н.В. К.82. Вища математика. Практикум. Навчальний посібник.–Київ: Центр навчальної літератури, 2005.–536с.
2. Бородин А.И., Бугай А.С., Биографический словарь деятелей в области математики. Радянська школа 1979.
3. Алгебра и начала анализа: В 2-х ч./ Под. ред. Г.Н. Яковлева.–2-е изд. –К.: Вища шк., Головное изд-во, 1984.–Ч.2. 293с.
| Формування у молодших школярів уміння розв'язувати текстові задачі | |
|
Дипломна робота Формування у молодших школярів уміння розв"язувати текстові задачі на знаходження невідомого компонента дій додавання і віднімання ... Під час таких бесід розкривати особливість математики як науки, її роль в житті кожної людини; розповідати, як учені-математики та інші фахівці дбають про правильність результатів ... Запис розв'язання виконують у вигляді прикладу, розміщеного посередині рядка. |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Формування в учнів умінь розв"язувати задачі на рух | |
|
Зміст Вступ 1. Теоретичні основи розв"язування задач на рух 1.1 Роль задач у початковому курсі математики 1.2 Місце задач на рух у системі складених ... Тут передбачено формування вмінь слухати задачу, повторити її детально або своїми словами, визначити відомі і невідомі величини, проаналізувати зміст задачі, зобразити задачу у ... Використовуючи навідні вказівки чи запитання, слід мати на увазі, що вказівки безпосередньо пов'язані з конкретним змістом задач, але взагалі вони бувають на зразок таких: це ... |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Графічні методи розв"язування задач із параметрами | |
|
... національний університет Кафедра математичного аналізу Факультет заочної та дистанційної освіти ДИПЛОМНА РОБОТА Графічні методи розв"язування ... мати один Розв"язання, що рівносильне для рівняння мати один корінь. В деяких прикладах цього параграфу ми будемо розв"язувати стандартну задачу: для прямої з сім"ї прямих знаходити її кутовий коефіцієнт, який відповідає моменту дотику з кривою. |
Раздел: Остальные рефераты Тип: дипломная работа |
| ... рівняння, нерівності та їх системи в шкільному курсі математики | |
|
... роботи мною була досягнута мета за допомогою виконання тих завдань, які були намічені, тобто: Систематизувала відомості про розв"язування показникових ... Поглиблений рівень - це, як правило задачі та вправи, розв"язання яких вимагає вміння орієнтуватися в нестандартних ситуаціях, застосовувати орігінальні та штучні прийоми, глибини ... Наведемо для прикладу один з можливих варіантів коментування учнем розв"язування рівняння 3. (в залежності від класу вчитель може допомогати при розв"язуванні, підказуючи, якщо ... |
Раздел: Рефераты по педагогике Тип: реферат |
| Розвиток творчої активності школярів у процесі розв"язування ... | |
|
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ Кафедра хімії Розвиток творчої активності школярів у процесі розв"язування розрахункових задач з хімії ЗМІСТ Вступ ... Високо оцінюючи наукове і практичне значення виконаних досліджень з проблем розвитку творчих здібностей учнів у процесі розв"язування хімічних задач, ми змушені зазначити, що на ... Також відомо, що люди з низьким рівнем інтелекту не можуть мати високий творчий потенціал, бо їм краще використовувати відомий шлях розв"язку, навіть тоді, коли необхідно розробити ... |
Раздел: Рефераты по педагогике Тип: курсовая работа |