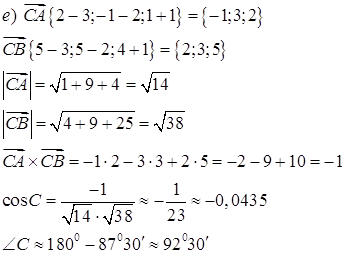Контрольная работа: Системы линейных уравнений

Вариант №9

№1. Решить систему линейных уравнений по правилу Крамера, с помощью обратной матрицы

a)         По правилу Крамера.

;

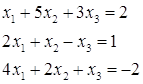
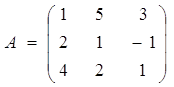
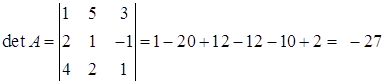
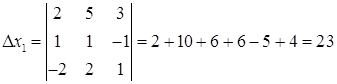
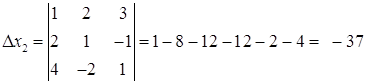
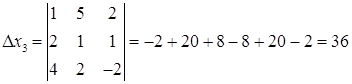
б) С помощью обратной матрицы.

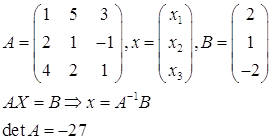
Алгебраические дополнения:

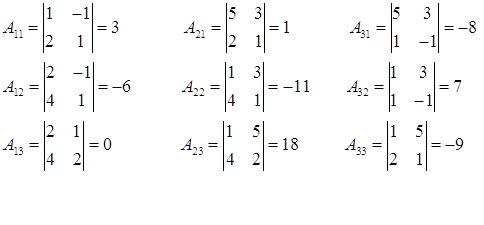
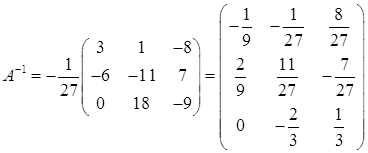
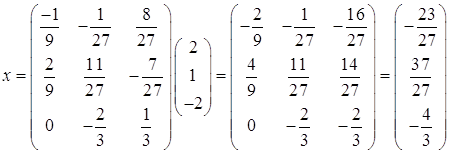
№ 2. Вычислить определитель

а) С помощью теоремы Лапласа. б) Предварительно упростив, получив нули в какой либо строке (столбце).

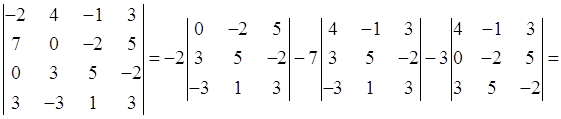
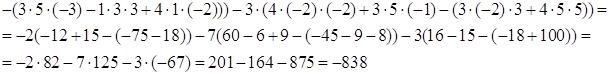
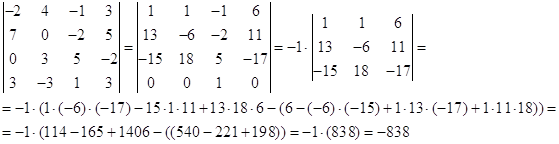
№3. Найти ранг матрицы

a)         С помощью элементарных преобразований

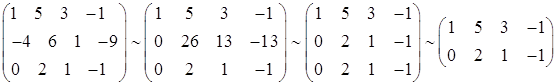
б) Найти ранг матрицы методом окаймления миноров

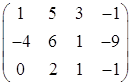
Решение. Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) М 1 = 1, расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор M 2=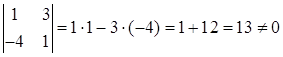, отличный от нуля. Переходим теперь к минорам 3-го порядка, окаймляющим М 2. Их всего два (можно добавить второй столбец или четвертый). Вычисляем их:

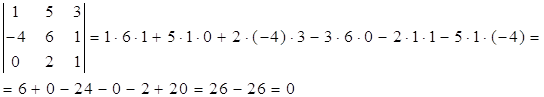
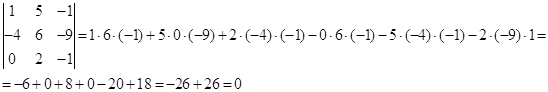
Таким образом, все окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.

№4. Дана система уравнений:

a) исследовать на совместимость б) Найти общее решение методом Гауса и записать два частных.

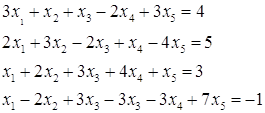
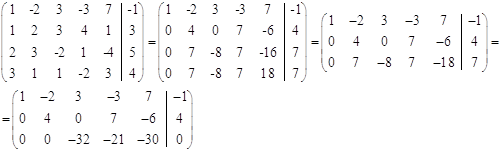
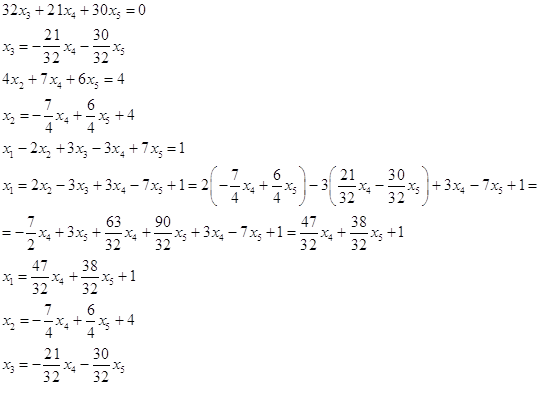
Частные решения:

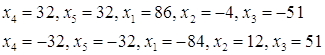
№5. Найти фундаментальную систему решений однородной системы уравнений

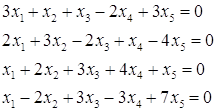
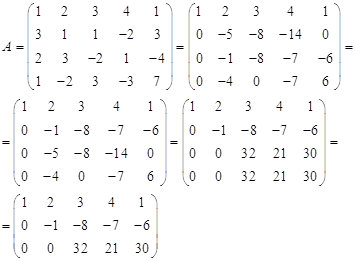
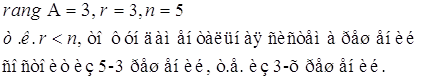
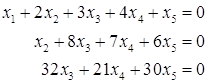
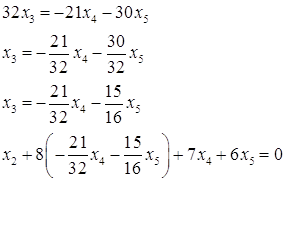
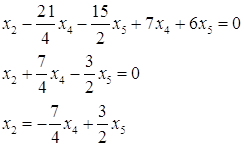
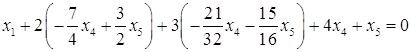
№ 6

a)         Найти площадь ABC

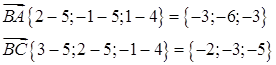
Найдем векторное произведение :

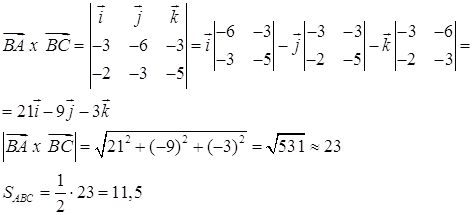
б) Составим уравнение плоскости ABC:

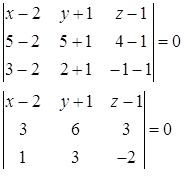
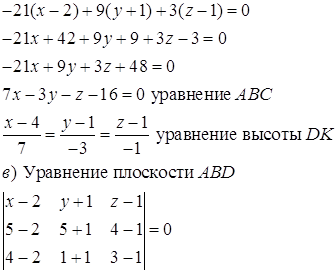
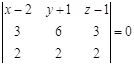
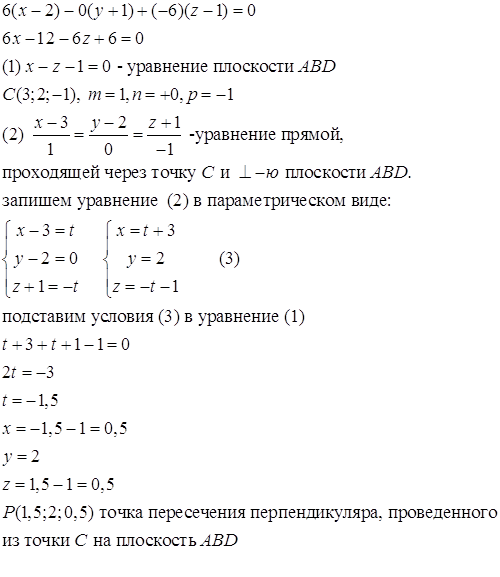
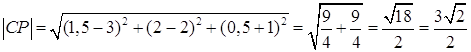
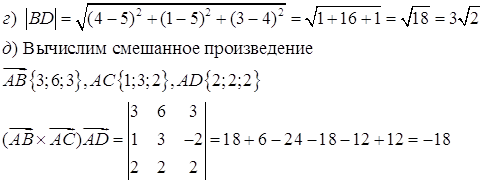
Объем параллелепипеда, построенного на трёх некомпланарных векторах , равен абсолютной величине их смешанного произведения, т.е. 18. Объем тетраэдра

e) Найти величину плоского угла при вершине С плоскости ABC