Курсовая работа: Теория вероятностей. От Паскаля до Колмогорова
Теория вероятностей. От Паскаля до Колмогорова
Санкт-Петербург 2010
Введение
Сейчас уже трудно установить, кто впервые поставил вопрос, пусть и в несовершенной форме, о возможности количественного измерения возможности появления случайного события. Мало-мальски удовлетворительный ответ на этот вопрос потребовал длительного времени и значительных усилий ряда поколений выдающихся исследователей. В течение долгого периода исследователи ограничивались рассмотрением разного рода игр, особенно игр в кости, поскольку их изучение позволяет ограничиваться простыми и прозрачными математическими моделями. Однако следует заметить, что многие отлично понимали то, что позднее было прекрасно сформулировано Христианом Гюйгенсом: «…я полагаю, что при внимательном изучении предмета читатель заметит, что имеет дело не только с игрой, но что здесь закладываются основы очень интересной и глубокой теории».
На первом этапе изучения случайных явлений внимание ученых было сосредоточено на трех задачах:
1) подсчет числа различных возможных исходов при бросании нескольких костей;
2) раздел ставки между игроками, когда игра прекращена где-то посередине;
3) определение числа бросаний двух или нескольких костей, при которых число случаев, благоприятствующих выпадению на всех костях одинаковых граней хотя бы при одном бросании, было большим, чем число случаев, когда это событие не появится ни разу.
Число различных исходов при бросании трех игральных костей было определено в 960 г. епископом Виболдом из города Камбрэ. Он считал, что таких исходов 56. Позднее выяснится, что это не так.
Попытка подсчитать число исходов при бросании трех игральных костей, включая и перестановки, имеется в поэме Ричарда де Форниваль, написанной в промежутке от 1220 до 1250 г. В части поэмы, посвященной играм и спорту, имеются следующие рассуждения: «Одинаковое число очков на трех костях можно получить шестью способами. Если число очков на двух костях совпадает, а на третьей от него отлично, то мы имеем 30 способов, поскольку одна пара могла быть выбрана шестью способами, а третье число лишь пятью. Если очки на всех костях различны, то мы имеем 20 способов, поскольку 30 раз по 4 равно 120, но каждая возможность появляется шестью способами. Таким образом, существует всего 56 возможностей.
Одинаковые числа очков на всех костях можно получить только единственным способом; одинаковые числа очков на двух костях, а третье отличное от них тремя способами».
Хотя в тексте явно указано лишь число случаев по Виболду, но фактически Ричард де Форниваль подготовил подсчет общего числа равновероятных случаев при бросании трех костей: 6*1+30*3+20*6 = 216.
Специального упоминания заслуживает одна из первых математических книг начала эпохи итальянского Возрождения, написанная Лукой Пачоли (1445–1514) и носившая название «Сумма знаний по арифметике, геометрии, отношениям и пропорциональности». В разделе необычных задач в упомянутой книге были помещены две следующие:
1) Компания играет в мяч до 60 очков и делает ставку в 22 дуката. В связи с некоторыми обстоятельствами игра прекращена до ее окончания, причем одна сторона в этот момент имеет 50, а другая – 30 очков. Спрашивается, какую долю общей ставки должна получить каждая сторона?
2) Трое соревнуются в стрельбе из арбалета. Кто первым достигнет 6 лучших попаданий, тот выигрывает. Ставка 10 дукатов. Когда первый получил 4, второй 3, а третий 2 лучших попадания, они не хотят продолжать и решают разделить приз справедливо. Спрашивается, какой должна быть доля каждого?
Пачоли предложил решение, которое позднее многократно оспаривалось, поскольку оно было признано ошибочным. А именно он предложил делить ставку пропорционально числу выигранных партий.
1. Исследования Дж. Кардано и Н. Тарталья
Существенное продвижение в решении первичных задач теории вероятностей связано с именами итальянских ученых Кардано (1501–1575) и Тарталья (1499–1557). В рукописи «Книга об игре в кости» были решены многие задачи, связанные с бросанием игральных костей и выпадением на них того или иного числа очков. Он правильно подсчитал числа различных случаев, которые могут произойти при бросании двух и трех костей. Кардано указал число возможных случаев появления хотя бы на одной из двух костей определенного числа очков. Кардано предложил рассматривать отношение 1/6 (вероятность выбрасывания заданного числа очков при бросании одной кости), 11/36 (вероятность получить хотя бы на одной из двух костей грань с заданным числом очков) которое мы теперь называем классическим определением вероятности. Кардано не заметил, что стоял на пороге введения важного понятия для всего дальнейшего развития большой главы математики, да и всего количественного естествознания. Рассматриваемые им отношения воспринимаются им скорее чисто арифметически, как доля случаев, чем как характеристика возможности появления случайного события при испытании. Кардано и Тарталья предложили новое решение задачи Пачоли о разделе ставки, однако и их решения были ошибочными.
2. Исследования Галилео Галилея
Таким образом, уже в 16 веке возникли задачи вероятностного характера и разыскивались подходы к их решению. Постепенно вырабатывались подходы, которые позднее становились основой новой теории и позволяли решать отдельные задачи. Значимый вклад в этот прогресс внес Галилео Галилей (1564–1642). Его работа «О выходе очков при игре в кости» была посвящена подсчету возможных случаев при бросании трех костей. Число всех возможных случаев Галилей подсчитал простым и естественным путем, возвел 6 (число различных возможностей при бросании одной кости) в 3 степень и получил 216. Далее он подсчитал число различных способов, которыми может быть получено то или другое значение суммы выпавших на костях очков. При подсчете Галилей пользовался полезной идеей: кости нумеровались (первая, вторая, третья) и возможные исходы записывались в виде троек чисел, причем на соответствующем месте стояло число очков, выпавшее на кости с данным номером. Эта простая мысль для своего времени оказалась весьма полезной.
Галилей, в сущности, повторил результаты, полученные значительно раньше рядом предшественников. Однако эта, теперь простая задача, в ту пору была серьезным испытанием и для мыслителя столь высокого ранга как Галилей.
Заметим, что у Галилея, как и у его предшественников, рассуждения ведутся не над вероятностями случайных событий, а над числами шансов, которые им благоприятствуют.
Для теории вероятностей и математической статистики большое значение имеют соображения Галилея по поводу теории ошибок наблюдений. До него никто этим не занимался. Таким образом, все, что он написал ан эту тему ново для его времени и важно даже в наши дни. Свои мысли и выводы он достаточно подробно изложил в одном из основных своих произведений: «Диалог о двух главнейших системах мира птолемеевой и коперниковой».
3. Вклад Паскаля и Ферма в развитие теории вероятностей
Обычно считают, что теория вероятностей зародилась в переписке двух великих ученых Б. Паскаля (1623–1662) и П. Ферма (1601–1665). От этой переписки сохранились лишь три письма Паскаля и четыре письма Ферма. В этой переписке еще отсутствует понятие вероятности, и оба ученых ограничиваются рассмотрением числа благоприятствующих событию шансов. У этих авторов впервые в истории имеется правильное решение задачи о разделе ставки, которая отняла много усилий у исследователей в течение длительного времени. Оба они исходили из одной и той же идеи: раздела ставки в отношении, пропорциональном вероятностям окончательного выигрыша каждого игрока. В предложенных ими решениях можно увидеть зачатки использования математического ожидания и теорем о сложении и умножении вероятностей. Это был серьезный шаг в создании предпосылок и интересов к задачам теоретико-вероятностного характера. Второй шаг был сделан также Паскалем, когда он существенно продвинул развитие комбинаторики и указал на ее значение для зарождающейся теории вероятностей. Толчком к появлению интересов Паскаля к задачам, приведшим к теории вероятностей, послужили встречи и беседы с придворным французского королевского двора шевалье де Мере, который интересовался литературой, философией и одновременно был страстным игроком. В этой страсти были истоки тех задач, которые он предложил Паскалю.
1) Сколько раз нужно подбросить две кости, чтобы число случаев, благоприятствующих выпадению хотя бы раз двух шестерок, было больше, чем число случаев, когда ни при одном бросании не появляются две шестерки одновременно?
2) Как нужно разделить ставки между игроками, когда они прекратили игру, не набрав необходимого для выигрыша числа очков?
Основное содержание писем Паскаля и Ферма посвящено разделу ставки. Решение Паскаля подробно излагается в письме:
«Вот примерно, что я делаю для определения стоимости каждой партии, когда два игрока играют, например, на три партии и каждым вложено по 32 пистоля.
Предположим, что один выиграл две партии, а другой одну. Они играют еще одну партию, и если выигрывает первый, то он получает всю сумму в 64 пистоля, вложенную в игру; если же эту партию выигрывает второй, то каждый игрок будет иметь по две выигранных партии и, следовательно, если они намерены произвести раздел, то каждый должен получить обратно свой вклад в 32 пистоля.
Примите же во внимание, монсеньер, что если первый выиграет, то ему причитается 64; если он проигрывает, то ему причитается 32. Если же игроки не намерены рисковать на эту партию, и хотят произвести раздел, то первый должен сказать: «Я имею 32 пистоля верных, ибо в случае проигрыша я их все равно получил бы, но остальные 32 пистоля могут быть получены либо мной, либо Вами, случайности равны. Разделим же эти 32 пистоля пополам, и дайте мне, кроме того, бесспорную сумму в 32 пистоля».
Далее Паскаль рассмотрел другой случай, когда первый игрок выиграл две партии, а второй ни одной и третий, когда первый игрок выиграл одну партию, а второй ни одной. В обоих случаях рассуждения те же, что были приведены выше.
Ферма предложил следующее решение этой задачи:
Пусть до выигрыша игроку А недостает двух партий, а игроку В трех. Тогда для завершения игры достаточно сыграть максимум четыре партии. Возможные исходы представлены в виде таблицы:
| ПАРТИИ | ||||
|
1 2 3 4 |
АААА АААВ ААВА ААВВ |
АВАА ВААВ ВААА АВАВ |
АВВА ВАВА ВВАА |
ВВВА ВВАВ ВАВВ АВВВ ВВВВ |
|
ИГРА ВЫИГРАНА ИГРОКОМ |
А после двух партий | А после четырех партий | А после трех партий | В после трех или четырех партий |
В первых одиннадцати исходах выигрывает А, в последних пяти В. Таким образом, ставка между игроками должна быть разделена в отношении 11/5. Т.е. игрок А получит 11/16, а В получит 5/16 ставки. Очевидно, что Ферма, как и Паскаль, делит ставку пропорционально вероятностям выигрыша каждым из игроков всей игры. Однако, они и сами не замечают, что их исходные позиции одинаковы.
Паскаль одновременно с
размышлениями над проблемами, составившими содержание его переписки с Ферма,
разрабатывал вопросы комбинаторики. Результатом этого явился «Трактат об
арифметическом треугольнике», внесший серьезный вклад в развитие комбинаторики.
В этом трактате есть параграф, в котором изложены правила использования
комбинаторных результатов в задаче о разделе ставки. Правило, предложенное Паскалем,
состоит в следующем: пусть игроку ![]() до
выигрыша всей игры не хватает
до
выигрыша всей игры не хватает ![]()
Партий, а
игроку ![]()
![]() партий, тогда ставка
должна делиться между игроками в следующем отношении:
партий, тогда ставка
должна делиться между игроками в следующем отношении:
![]()
4. Работа Х. Гюйгенса
Значительное влияние на развитие теории вероятностей оказала работа Х. Гюйгенса (1629–1695). Интерес Гюйгенса к этим вопросам был вызван его поездкой в Париж в 1655 г., где он познакомился с рядом видных ученых и услышал от них сведения относительно задач о разделе ставки в азартных играх, которые разрабатывались Паскалем и Ферма. Результатом явилась его работа, опубликованная в 1656 г. в виде дополнения к книге его учителя Ф. ван Схоутена «Математические этюды».
Работа Гюйгенса состоит из небольшого введения и 14 предложений. Эти предложения весьма различны по своему содержанию. Первые три являются теми принципами, на основе которых Гюйгенс основывал последующие решения.
Предложение
1. Если я имею равные шансы получить ![]() или
или ![]() , то это мне стоит
, то это мне стоит ![]() .
.
Предложение
2. Если я имею равные шансы получить ![]() или
или ![]() , то это мне стоит столько
же, как если бы я имел
, то это мне стоит столько
же, как если бы я имел ![]() .
.
Предложение
3. Если число случаев, в которых получается сумма ![]() ,
равно
,
равно ![]() , а число случаев, в
которых получается сумма
, а число случаев, в
которых получается сумма ![]() , равно
, равно ![]() , то стоимость моего
ожидания равна
, то стоимость моего
ожидания равна ![]() .
.
Ясно, что
этими предложениями Гюйгенс ввел понятие математического ожидания для
случайной величины, принимающей два или три значения. В первых двух
предложениях значения, принимаемые случайными величинами, равновероятны, а в
третьем предложении вероятность значения ![]() равна
равна
![]() и вероятность значения
и вероятность значения ![]() равна
равна ![]() . Понятие вероятности у Гюйгенса
еще не выделено, и он все время оперирует числами шансов, благоприятствующих тому
или другому событию. Гюйгенс говорил о стоимости, за которую он готов
уступить свое право на получение выигрыша. Термин «ожидание» был введен в
употребление Схоутеном при переводе.
. Понятие вероятности у Гюйгенса
еще не выделено, и он все время оперирует числами шансов, благоприятствующих тому
или другому событию. Гюйгенс говорил о стоимости, за которую он готов
уступить свое право на получение выигрыша. Термин «ожидание» был введен в
употребление Схоутеном при переводе.
Предложения 1 и 2 представляют собой ничто иное, как версию задачи о разделе ставки.
«Предположим,
что я играю против другого лица на то, кто первым выиграет 3 партии, и что я
уже выиграл 2 партии, а он 1. Я хочу знать, какая часть ставки причитается мне,
когда мы хотим прервать игру и справедливо разделить ставки… Нужно заметить
сначала, что достаточно принять во внимание число партий недостающих той и
другой стороне. Так как верно, что если бы мы играли на то, кто выиграет 20
партий, и если бы я выиграл 19 партий, а мой противник 18, то я имел бы такое
же самое преимущество, как и в изложенном случае, где при трех партиях я
выиграл две, а он только одну, а это потому, что в обоих случаях мне недостает
только одной партии, а ему двух. Затем, чтобы вычислить часть, причитающуюся
каждому из нас, нужно обратить внимание на то, что произошло бы, если бы мы
продолжали игру. Верно и то, что выиграв партию, я получил бы полностью сумму
ставки, которую обозначу ![]() . Но
если первую партию выиграет мой противник, то наши шансы станут равными,
принимаю во внимание, что каждому из нас будет недоставать по одной партии;
значит, каждый из нас имел бы право на
. Но
если первую партию выиграет мой противник, то наши шансы станут равными,
принимаю во внимание, что каждому из нас будет недоставать по одной партии;
значит, каждый из нас имел бы право на ![]() ,
что согласно первому предложению, эквивалентно сумме половин, т.е.
,
что согласно первому предложению, эквивалентно сумме половин, т.е. ![]() , так что моему сопернику
остается
, так что моему сопернику
остается ![]() ».
».
Предложения 4–9 работы Гюйгенса посвящены решению задач, связанных с безобидным делением ставки. Например, в предложении 8 рассмотрено деление ставки между тремя игроками, когда первому игроку недостает до выигрыша всей игры одной партии, а второму и третьему по две. Предложения 10–14 содержат различные задачи, связанные с бросанием костей. В конце работы помещены 5 задач без решений, которые Гюйгенс предложил читателю для самостоятельных размышлений.
К концу 17 века завершался длительный период накопления первичных сведений о случайных событиях, точно поставленных задач и подходов к их решению. Многие выдающиеся умы занимались этими вопросами и с разных позиций подходили к количественной оценки возможности наступления случайного события. Ферма фактически пользовался понятием математического ожидания, использование которого для решения разнообразных задач было широко развито Гюйгенсом; Паскаль, Ферма и Гюйгенс использовали представления о теоремах сложения и умножения вероятностей, и подошли вплотную к понятию вероятности, однако его они не ввели. Если бы исследователи того времени задали себе вопрос, что возможнее при четырехкратном бросании кости хотя бы раз выбросить шестерку или при двадцатипятикратном бросании двух костей хотя бы раз выбросить на обеих костях шестерки, они были бы вынуждены ввести классическое понятие вероятности и далее его использовать. Однако этого в 17 веке не произошло и введение в науку классического понятия вероятностей принадлежит лишь 18 столетию. Период предыстории завершался и начинался период истории теории вероятностей. Для этого уже был создан достаточно прочный фундамент.
5. Первые исследования по демографии
Одним из толчков для развития основных понятий теории вероятностей сыграли исследования Джона Граунта (1620–1675) и Вильяма Петти (1623–1687) по демографии. Их работы наглядно продемонстрировали, каким мощным орудием могут служить для изучения массовых явлений статистические наблюдения, если их соответствующим образом обработать. Первой работой, с которой начинается история статистики как области научного знания, следует назвать книгу Граунта, опубликованную в 1662 г. под названием «Естественные и политические наблюдения, перечисленные в прилагаемом оглавлении и сделанные над бюллетенями смертности. По отношению к управлению, религии, торговле, росту, воздуху, болезням и разным изменениям означенного города».
Основная задача, которая интересовала Граунта, состояла в указании метода, который позволял бы установить с достаточной точностью возрастной состав населения города в результате наблюдений за возрастом умерших. С этой целью им были проанализированы 229 250 регистраций смертей в Лондоне происшедших за 20 лет. Среди этих смертей было отмечено 71 124 смерти детей от 0 до 6 лет. Причины смертей были тщательно перечислены Граунтом. Он специально отметил, что отношение числа смертей детей от 0 до 6 лет к общему числу смертей за тот же период времени, равное 71 124/229 250, приблизительно равняется 1/3. Иными словами, Граунт ввел представление о частоте события. Для развития теории вероятностей это обстоятельство сыграло огромную роль, как и его замечание: «…мы бы хотели отметить, что некоторые из случайностей имеют постоянное отношение к числу всех похорон». Здесь Граунт вплотную подошел к представлению о статистической устойчивости средних. Им была составлена первая таблица смертности.
Граунт прекрасно понимал, что точность его выводов тем больше, чем больше наблюдений имеется для обработки. Именно в связи с этим он отметил, что недостаточно ограничиваться обработкой бюллетеней смертности только за одну неделю для получения полноценных выводов о составе населения.
Понятие частоты подхватили другие авторы. Так в небольшой книге В. Петти «Два очерка по политической арифметике, относящиеся к людям, зданиям, больницам в Лондоне, Париже», вышедшей в 1682 г. в Лондоне, а через два года во французском переводе в Париже, были даны сравнительные данные о смертности в госпиталях шарите Парижа и Лондона.
Работы Граунта, Петти и ряда их последователей представляют собой ничто иное, как первые шаги в области математической статистики.
Непосредственным продолжателем исследований, начатых Граунтом и Петти, был знаменитый английский астроном Эдмунт Галлей (1656–1742). В 1693 г. Галлей опубликовал в изданиях Лондонского королевского общества две статьи «Оценка степеней смертности человечества, выведенная на основании любопытных таблиц рождений и погребений города Бреславля, с попыткой установить цену пожизненных рент» и «Несколько дальнейших замечаний по поводу Бреславльских бюллетеней смертности». Одна из причин интереса Галлея к таблицам смертности состоит в том, что сами Граунт и Петти сознавали недостаточную обоснованность своих выводов, поскольку у них отсутствовали численность населения и возраст умерших. Кроме того, в городах, которые они изучали, был большой приток населения извне. Это обстоятельство делает указанные города «неподходящими в качестве стандарта для этой цели, которая требует, если это возможно, чтобы население, с которым имеют дело, было совершенно закрытым, т.е. таким, где все умирают там, где они родились, где нет никаких эмигрантов и иммигрантов. По словам Галлея, бреславльские материалы не имеют указанных дефектов.
На основании имевшихся у него данных Галлей составил таблицу смертности, которую он рассматривал одновременно и как таблицу доживающих по возрасту лиц, так и как распределение населения по возрасту. Он ввел в науку понятие о вероятной продолжительности жизни, как о возрасте, которого одинаково можно достигнуть и не достигнуть. На современном языке это медиана длительности жизни. В вычислениях Галлея можно заметить использование им принципов, лежащих в основе теорем сложения т умножения вероятностей, а также рассуждения, близкие к формулировке закона больших чисел.
Работы Галлея имели очень большое значение для развития науки и применений статистических исследований о народонаселении к вопросам страхования.
6. Возникновение классического определения вероятности
До конца 17 в. наука так и не подошла к введению классического определения вероятности. Однако в 30-х годах 18-го столетия классическое определение вероятности стало общеупотребительным, и никто из ученых этих лет не мог бы ограничиться только подсчетом числа благоприятствующих событию шансов. Введение классического определения вероятности произошло не в результате однократного действия, а заняло длительный промежуток времени, на протяжении которого происходило непрерывное совершенствование формулировки, переход от частных задач к общему случаю. Еще в книге Гюйгенса «О расчетах в азартных играх» (1657) нет понятия вероятности как числа, заключенного между 0 и 1 и равного отношению числа благоприятствующих событию шансов к числу всех возможных. А в трактате Я. Бернулли «Искусство предположений» (1713) понятие это введено, хотя и в несовершенной форме. Что же заставило Бернулли ввести в научный обиход классическое понятие вероятности?
Несомненно, что формулировка закона больших чисел, осуществленная Бернулли, сама по себе является достаточным для этого основанием. Однако сильное влияние на ход мыслей ряда исследователей, в том числе и Бернулли, оказали работы Граунта и Петти. Их произведения убедительно показали преимущества понятие частоты перед понятием численности. Понятие частоты, т.е. отношение числа наблюдений, в которых появляется определенное свойство, к числу всех наблюдений, позволяет получить серьезные практические выводы. Отсюда оставался один шаг до введения классического определения вероятности. Выводы Граунта и Петти относительно устойчивости некоторых событий подготовили почву и к формулировке закона больших чисел.
Бернулли дал такое определение вероятности: «Вероятность есть степень достоверности и отличается от нее, как часть от целого». Далее было пояснение сказанного на примере, который показывает, что Бернулли в данную им формулировку вкладывал тот же смысл, какой мы вкладываем в классическое определение вероятности.
Интересны другие рассуждения его работы. Бернулли задал вопрос: как определить вероятность случайного события, если у нас нет возможности подсчитать числа всех возможных и благоприятствующих ему шансов? Ответ был им сформулирован следующим образом: «Но здесь нам открывается другая дорога для достижения искомого. И то, что не дано вывести a priori, то, по крайней мере, можно получить a posteriori, т.е. из многократного наблюдения результатов в подобных примерах… Ибо, если, например, при наблюдениях, сделанных некогда над тремя сотнями людей того же возраста и сложения, в каких находится теперь Тит, было замечено, что из них двести до истечения 10 лет умерли, а остальные остались в живых и дальше, то можно заключить с достаточным основанием, что имеется вдвое больше случаев Титу умереть в течение ближайшего десятилетия, чем остаться в живых по истечении этого срока… Этот опытный способ определения числа случаев по наблюдениям не нов и не необычен».
Важно подчеркнуть, что в высказанных отрывках достаточно четко прослеживается мысль о статистическом определении вероятности. Таким образом, в трактате Бернулли присутствуют обе концепции вероятности классическая и статистическая. Обе они изложены не очень четко, но они уже введены в рассмотрение и использованы. Введено в рассмотрение понятие вероятности случайного события, как числа, заключенного между 0 и 1. Достоверному событию приписывается максимально возможное значение вероятности единица, а невозможному минимальное ноль. Кроме того, было ясно сказано, что это число может быть определено двумя различными способами: путем подсчета числа равновозможных случаев, которые благоприятствуют событию, и всех возможных случаев и вычисления их отношения или же путем проведения большого числа независимых испытаний и вычисления частоты события.
Монмор в своей книге «Обзор
анализа азартных игр» использовал введенное Бернулли понятие вероятности
и применил его к решению достаточно сложных задач. В частности Монмор
рассмотрел и правильно решил следующую задачу: имеется ![]() предметов, пронумерованных
числами от 1 до
предметов, пронумерованных
числами от 1 до ![]() . Спрашивается,
чему равна вероятность того, что при последовательном вынимании этих предметов
наудачу (без возвращения) хотя бы один предмет будет вынут так, что номер
вынимания совпадет с присвоенным ему номером. Эта вероятность оказалась равной
. Спрашивается,
чему равна вероятность того, что при последовательном вынимании этих предметов
наудачу (без возвращения) хотя бы один предмет будет вынут так, что номер
вынимания совпадет с присвоенным ему номером. Эта вероятность оказалась равной ![]() .
.
А. Муавр принял классическое определение вероятности, данное Бернулли, и вероятность события определил в точности так, как это делаем мы теперь. Он писал: «Следовательно, мы строим дробь, числитель которой будет число случаев появления события, а знаменатель число всех случаев, при которых оно может появиться или не появиться, такая дробь будет выражать действительную вероятность его появления». Муавр, как и Бернулли не заострял внимание на то, что шансы должны быть равновероятными. Это замечание впервые было введено в определение классической вероятности лишь П. Лапласом в его «Аналитической теории вероятностей». Лагранж об этом еще не задумывался и давал определение вероятности в точности по Муавру. По-видимому, на Лапласа повлияла дискуссия, начатая Д`Аламбером, который при решении задачи о вероятности выпадения (при бросании двух монет) герба на одной из монет и решки на другой, определил ее равной 1/3. Это он мотивировал тем, что имеется лишь три возможности:
1) на обеих монетах выпадает герб;
2) на обеих монетах выпадает решка;
3) на одной монете выпадает герб, а на другой решка.
7. Формирование понятия геометрической вероятности
Уже в первой
половине 18 века выяснилось, что классическое понятие вероятности имеет
ограниченную область применений и возникают ситуации, когда оно не действует, а
потому необходимо какое-то естественное его расширение. Обычно считают, что
таким толчком послужили работы французского естествоиспытателя Ж. Бюффона
(1707–1788), в которых он сформулировал знаменитую задачу о бросании иглы на
разграфленную плоскость и предложил ее решение. Однако, задолго до рождения Бюффона
появилась работа, в которой фактически уже был поставлен вопрос о нахождении
геометрической вероятности. В 1692 г. в Лондоне был опубликован английский
перевод книги Х. Гюйгенса «О расчетах в азартных играх»,
выполненный Д. Арбутнотом (1667–1735). В конце первой части
переводчик добавил несколько задач, среди которых была сформулирована задача
совсем иной природы, по сравнению с теми, которые были рассмотрены великим
автором. Он назвал эту задачу трудной и поместил ее в дополнении «для того,
чтобы она была решена теми, кто считает такого рода проблемы достойными
внимания». Задача, предложенная Арбутнотом состоит в следующем: на
плоскость наудачу бросается прямоугольный параллелепипед, с ребрами, равными ![]() ,
,![]() ,
,![]() . Спрашивается, как часто
параллелепипед будет выпадать гранью
. Спрашивается, как часто
параллелепипед будет выпадать гранью ![]() ? Сам Арбутнот
не сделал даже попытки решить придуманную им задачу. Это было осуществлено
значительно позднее Т. Симпсоном (1710–1761) в книге «Природа и
законы случая». Идея решения состоит в следующем: опишем около параллелепипеда
сферу и спроектируем из центра на поверхность ее все ребра, боковые грани и
основания. В результате поверхность сферы разобьется на шесть непересекающихся
областей, соответствующих граням параллелепипеда. «Нетрудно заметить, что
определенная часть сферической поверхности, ограниченная траекторией, описанной
таким образом радиусом, будет находиться в таком же отношении к общей площади
поверхности, как вероятность появления некоторой грани к единице». Здесь
заключены принципы разыскания геометрических вероятностей: вводится мера
множества благоприятствующих событию случаев и берется ее отношение к мере
множества всех возможных случаев. В нашем случае полная мера сводится к площади
поверхности шара.
? Сам Арбутнот
не сделал даже попытки решить придуманную им задачу. Это было осуществлено
значительно позднее Т. Симпсоном (1710–1761) в книге «Природа и
законы случая». Идея решения состоит в следующем: опишем около параллелепипеда
сферу и спроектируем из центра на поверхность ее все ребра, боковые грани и
основания. В результате поверхность сферы разобьется на шесть непересекающихся
областей, соответствующих граням параллелепипеда. «Нетрудно заметить, что
определенная часть сферической поверхности, ограниченная траекторией, описанной
таким образом радиусом, будет находиться в таком же отношении к общей площади
поверхности, как вероятность появления некоторой грани к единице». Здесь
заключены принципы разыскания геометрических вероятностей: вводится мера
множества благоприятствующих событию случаев и берется ее отношение к мере
множества всех возможных случаев. В нашем случае полная мера сводится к площади
поверхности шара.
Бюффон дважды публиковал
работы, посвященные геометрическим вероятностям. Первая публикация относится к
1733 г., когда он сделал в Парижской академии наук доклад, напечатанный
под названием «Мемуар об игре под названием франк-карро». Цель, которую ставил
перед собой Бюффон, состояла в том, чтобы показать, что «геометрия может
быть использована в качестве аналитического инструмента в области теории
вероятностей», в то время, как до тех пор «геометрия казалась мало пригодной
для этих целей», поскольку для них использовалась только арифметика. Игра
франк-карро состоит в следующем: пол разграфлен на одинаковые фигуры. На пол
бросается монета, ее диаметр ![]() меньше
каждой из сторон и монета целиком укладывается внутрь фигуры. Чему равна
вероятность того, что брошенная наудачу монета пересечет одну или две стороны
фигуры?
меньше
каждой из сторон и монета целиком укладывается внутрь фигуры. Чему равна
вероятность того, что брошенная наудачу монета пересечет одну или две стороны
фигуры?
Для
определенности рассмотрим покрытие плоскости прямоугольниками со сторонами ![]() ,
, ![]() . Легко подсчитать, что
площадь полосы между основным прямоугольником со сторонами, параллельными
сторонам основного на расстоянии
. Легко подсчитать, что
площадь полосы между основным прямоугольником со сторонами, параллельными
сторонам основного на расстоянии ![]() от
каждой из его сторон и целиком расположенного внутри основного, равна
от
каждой из его сторон и целиком расположенного внутри основного, равна ![]() . Легко понять, что центр
монеты, попав внутрь малого прямоугольника, не только не пересечет, но даже не
коснется сторон основного. Значит, вероятность того, что монета пересечет по
меньшей мере одну из сторон основного прямоугольника равна
. Легко понять, что центр
монеты, попав внутрь малого прямоугольника, не только не пересечет, но даже не
коснется сторон основного. Значит, вероятность того, что монета пересечет по
меньшей мере одну из сторон основного прямоугольника равна ![]() .
.
Вторая задача, сформулированная Бюффоном, состоит в следующем: плоскость разграфлена равноотстоящими параллельными прямыми. На плоскость наудачу бросается игла. Один игрок утверждает, что игла пересечет одну из параллельных прямых, другой, что не пересечет. Определить вероятность выигрыша каждого из игроков. Менее известна задача об игре, когда игла бросается на плоскость, разграфленную на квадраты. В решении этой задачи Бюффон допустил ошибку, позднее исправленную Лапласом.
После Бюффона задачи на геометрические вероятности стали систематически включаться в трактаты и учебники по теории вероятностей. В прекрасном для своего времени учебнике «Основания математической теории вероятностей» (1846) В.Я. Буняковского (1804–1889) имеется большой раздел, посвященный геометрической вероятности. В него включена задача Бюффона о бросании иглы и частный случай игры франк-карро, когда плоскость разбита на равнобедренные треугольники.
Серьезный шаг в развитии геометрических вероятностей связан с именами Ламе (1795–1870), Барбье, Д. Сильвестра (1814–1897), М. Крофтона, которые не просто поставили новые задачи, но и привлекли к их решению понятие меры множества. На базе их рассмотрений позднее возникла новая ветвь геометрии, получившая название интегральная геометрия.
Сильвестр первый после Бюффона расширил тематику задач на геометрические вероятности. Им была предложена задача о четырех точках или задача Сильвестра: четыре точки взяты наудачу внутри выпуклой области. Чему равна вероятность того, что, взяв эти точки в качестве вершин, можно составить выпуклый четырехугольник?
Сильвестр отчетливо понимал, что при вычислении геометрических вероятностей приходится брать отношение площадей или объемов тех областей, которые благоприятствуют событию и в которых помещаются всевозможные события. Фактически так поступали и раньше. Но при этом произносили другие слова, которые или не имели определенного смысла или же не соответствовали производимым действиям. Сравнив результаты вычислений для различных областей, Сильвестр предложил найти те области, для которых вероятность получения выпуклого четырехугольника достигает максимума или минимума. Первые результаты принадлежат Крофтону. Он доказал, что минимум достигается для круга. Там же он высказал предположение, что минимум достигается и для эллипса. Это предложение было доказано лишь В. Блашке (1923). Дельтейль показал, что максимальная вероятность формирования выпуклого четырехугольника достигается для треугольной области. Несомненно, что в 19 веке на развитие проблематики геометрических вероятностей особое влияние оказал Крофтон. Он начал изучать пересечение случайными прямыми заданных выпуклых контуров.
На необходимость совершенствования понятия геометрической вероятности несомненное влияние оказала книга Ж. Бертрана (1822–1900), в которой на хорошо подобранных примерах было показано, что логически понятие геометрической вероятности не выдерживает критики. Играя на неопределенности терминологии, казалось бы для одной и той же задачи, ему удалось получить несколько разных ответов. В качестве основной мишени им была выбрана задача о проведении наудачу хорды внутри круга. Критика Бертрана привлекла внимание математиков к общим вопросам логического обоснования теории вероятностей.
В 20 веке интерес к геометрическим вероятностям не ослабел, а вырос, поскольку, помимо чисто математического интереса, они приобрели серьезное прикладное значение в физике, биологии, медицине, инженерном деле и т.д.
8. Основные теоремы теории вероятностей
Следующий важный вопрос: кто и когда выделил в теории вероятностей основные ее теоремы сложения, умножения и полной вероятности? Формулировки этих теорем не удалось заметить ни в переписке Ферма с Паскалем, ни в трактате Гюйгенса. Однако зачатки этих теорем можно проследить буквально с первых шагов теории вероятностей как математической науки.
Так в работах
Паскаля можно увидеть, что он отчетливо понимал как следует подсчитывать
число благоприятствующих шансов для события ![]() ,
если нам известны шансы для несовместимых событий
,
если нам известны шансы для несовместимых событий ![]() ,
составляющих событие
,
составляющих событие ![]() . Это, конечно,
еще не теорема сложения, но важный шаг на пути ее формулировки. В работах Я. Бернулли
и Н. Бернулли дается отчетливая формулировка правило числения
вероятности противоположного события, если известна вероятность прямого.
. Это, конечно,
еще не теорема сложения, но важный шаг на пути ее формулировки. В работах Я. Бернулли
и Н. Бернулли дается отчетливая формулировка правило числения
вероятности противоположного события, если известна вероятность прямого.
Первая четкая и окончательная формулировка теорема сложения вероятностей находится в работе Т. Байеса (1702–1761), носящей название «Опыт решения задач по теории вероятностей покойного достопочтенного мистера Байеса, члена Королевского общества. Сообщено мистером Прайсом в письме Джону Кентону, магистру искусств, члену Королевского общества». В этой работе содержится определение несовместимых событий. Байес употребляет другой термин «неплотные события». По Байесу «несколько событий являются неплотными, если наступление одного из них исключает наступление других». Байес сформулировал теорему сложения в следующем виде: «Если несколько событий являются неплотными, то вероятность того, что наступит какое-то из них, равно сумме вероятностей каждого из них».
Четкое выделение теоремы умножения было осуществлено Муавром в 1718 г. Во введении к «Доктрине шансов» он определил важное понятие независимости случайных событий: «Мы скажем, что два события независимы, когда каждое из них не имеет никакого отношения к другому, а появление одного из них не оказывает никакого влияния на появление другого». Еще более определенно им дано определение зависимых событий: «два события зависимы, когда они связаны друг с другом и когда вероятность появления одного из них изменяется при появлении другого». Теорему умножения Муавр сформулировал следующим образом: «…вероятность появления двух независимых событий равна произведению вероятности появления одного из них на вероятность того, что другое должно появиться, если первое из них уже появилось. Это правило может быть обобщено на случай нескольких событий».
О вероятности совместного наступления нескольких событий Муавр писал следующее «…надо обозначить одно из них как первое, другое как второе и т.д. Тогда вероятность появления первого должна рассматриваться как независимая от остальных, вторая – в предположении, что первое произошло, третье – в предположении наступления первого и второго и т.д. Следовательно, вероятность наступления всех событий равна произведению всех только что указанных вероятностей». Муавр отметил, что разыскание условных вероятностей, как правило, представляет собой сложное занятие.
Формулировка
теоремы умножения у Байеса такая же, как у Муавра. Единственно, в
чем Байес пошел дальше Муавра это в формулировке следствия о
вычислении вероятности ![]() по вероятностям
по вероятностям ![]() и
и ![]() . Это предложение дало
основание приписывать Байесу формулы, носящие его имя. В
действительности у него их нет, поскольку он не знал формулы полной вероятности.
. Это предложение дало
основание приписывать Байесу формулы, носящие его имя. В
действительности у него их нет, поскольку он не знал формулы полной вероятности.
Результат, приписываемый Байесу, по-видимому, впервые получил современную формулировку у Лапласа в его «Опыте философии теории вероятностей». В главе «Общие принципы теории вероятностей» он сформулировал принцип, который относится к вероятности гипотез, или, как писал Лаплас, вероятности причин, словесно сформулировал известное «правило Байеса». Более того, этот принцип Лапласа содержит и формулу полной вероятности.
Таким образом, основные принципы действия с вероятностями вычленялись длительным путем. Их многократно использовали при решении отдельных задач, но не формулировали их в качестве особых предложений. Потребовалось почти целое столетие, чтобы после введения в науку понятия вероятности сформулировать для этого понятия систему правил действия с ним. Такие правила широко использовались фактически, но потребности в их формулировании не ощущали. Попутно при этом вводились и дополнительные понятия, которые позволяли глубже вникать в природу вещей. В нашем случае этими понятиями являются понятия несовместимости и независимости случайных событий.
9. Задача о разорении игрока
Серьезную роль в развитии теории вероятностей играла задача о разорении игрока, она позволяла оттачивать методы решения сложных вопросов и в какой-то мере являлась исходным пунктом для развития теории случайных процессов. Именно в этой задаче впервые начали изучать состояние системы в зависимости от времени. Точнее положение игроков после заданного числа партий. Эта задача была впервые сформулирована в Гюйгенсом в книге «О расчетах в азартных играх». Этой задачей занимались многие выдающиеся математики Я. Бернулли, Н. Бернулли, Муавр, Лаплас и др.
Первые
подходы к решению задачи о разорении игрока почти одновременно были предложены
тремя математиками Монмором, Муавром и Н. Бернулли. Их
результаты относились к 1710–1711 г. Задача Гюйгенса в их
формулировке слегка преобразилась и приобрела привычный для нас вид: игроки ![]() и
и ![]() имеют соответственно
имеют соответственно ![]() и
и ![]() франков и при каждой
партии некоторой игры один из них выигрывает у другого 1 франк. Вероятность
выигрыша игрока
франков и при каждой
партии некоторой игры один из них выигрывает у другого 1 франк. Вероятность
выигрыша игрока ![]() для каждой
партии равна
для каждой
партии равна ![]() , для игрока
, для игрока ![]() вероятность выигрыша равна
вероятность выигрыша равна
![]() . Спрашивается, чему равны
вероятности
. Спрашивается, чему равны
вероятности ![]() и
и ![]() того, что игрок
того, что игрок ![]() выиграет (соответственно
игрок
выиграет (соответственно
игрок ![]() ) игру (т.е. игрок
) игру (т.е. игрок ![]() выиграет все деньги
выиграет все деньги ![]() раньше, чем
раньше, чем ![]() выиграет их у
выиграет их у ![]() ).
).
Муавр нашел, что
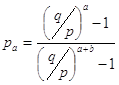 ,
, 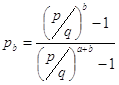 .
.
И что
математическое ожидание числа ![]() необходимых
для завершения игры партий равно
необходимых
для завершения игры партий равно ![]() .
.
Ему же
удалось найти вероятности ![]() , что
игрок
, что
игрок ![]() выиграет игру за
выиграет игру за ![]() партий (соответственно
выиграет за
партий (соответственно
выиграет за ![]() партий игрок
партий игрок ![]() ). Вдобавок им был подробно
рассмотрен случай, когда
). Вдобавок им был подробно
рассмотрен случай, когда ![]() .
.
В 1710 г.
формулы для ![]() в случае
в случае ![]() нашел Монмор. Свои
соображения он переслал Иоганну Бернулли, который передал письмо своему
племяннику Николаю. Ответное письмо Н. Бернулли от 26 февраля 1711 г.
содержало решение и для случая
нашел Монмор. Свои
соображения он переслал Иоганну Бернулли, который передал письмо своему
племяннику Николаю. Ответное письмо Н. Бернулли от 26 февраля 1711 г.
содержало решение и для случая ![]() .
.
Рассмотрение решений этих ученых ясно показывает, что все они владели приемами оперирования с вероятностями сложных событий. Практически они безукоризненно точно использовали теоремы сложения и умножения вероятностей, а также формулу полной вероятности, хотя в ту пору они еще не получили точной формулировки. Происходило накопление опыта и выделение тех правил, которые постоянно необходимы при подсчете вероятностей сложных событий.
10. Возникновение предельных теорем теории вероятностей
На последующее развитие теории вероятностей огромное воздействие оказала идея, впервые высказанная и осуществленная Я. Бернулли рассматривать не только точные решения задач теории вероятностей, но и их асимптотические постановки при неограниченном увеличении некоторого параметра. В первую очередь следует указать на закон больших чисел в форме Я. Бернулли. Именно он послужил источником для различного рода уточнений как в 18-ом веке, так и в последующие столетия.
Я. Бернулли дал формулировку своей теоремы в отличном от принятого теперь виде, использовал для обозначения испытаний, при которых интересующее нас событие происходит, слова «плодовитый», «фертильный», а для противоположных исходов слово «стерильный».
«Пусть число
фертильных случаев к числу стерильных случаев относится точно или приближенно
как ![]() или же это число относится
к числу всех случаев как
или же это число относится
к числу всех случаев как ![]() или же
как
или же
как ![]() . Последнее отношение
находится, следовательно, между
. Последнее отношение
находится, следовательно, между ![]() и
и ![]() . Нужно доказать, что можно
произвести столь большое число опытов, что число появившихся фертильных
наблюдений к числу всех опытов будет больше, чем
. Нужно доказать, что можно
произвести столь большое число опытов, что число появившихся фертильных
наблюдений к числу всех опытов будет больше, чем ![]() ,
и меньше, чем
,
и меньше, чем ![]() ». Ясно, что эта
формулировка лишь словесно отличается от принятой теперь.
». Ясно, что эта
формулировка лишь словесно отличается от принятой теперь.
Книга «Искусство предложений» Я. Бернулли быта тщательно изучена его племянником Н. Бернулли. В его работе «О применении искусства предположений в вопросах прав», исходя из таблиц Граунта, он изучал вопрос о вероятности дожития до определенного возраста. На основании долголетних регистраций рождений он отметил тот факт, что мальчиков рождается больше, чем девочек. При этом отношение числа рождений мальчиков к числу рождений девочек оказывается, как он считал, равным 18:17.
Далее Н. Бернулли
рассмотрел пример, когда имеется 14 000 рождений. Тогда, согласно формулам
Н. Бернулли, имеет место равенство (![]() означает
фактическое число рождений мальчиков)
означает
фактическое число рождений мальчиков)
![]()
Фактическое число рождений мальчиков зависит от случая. Приведенная формула позволяет вычислить вероятность того, что число рождений мальчиков будет заключено в указанных границах. Однако вычисления, которые при этом необходимо произвести, сложны.
В точности
этот пример рассмотрен Лапласом в «Аналитической теории вероятностей». В
качестве искомого значения вероятности неравенства ![]() Лаплас
указал величину 0.994303.
Лаплас
указал величину 0.994303.
В двух
последних изданиях книги Муавра «Доктрина шансов» был помещен перевод
его статьи 1733 г. Согласно словам самого автора «Я помещаю здесь перевод
моей работы, написанной 12 ноября 1733 года и сообщенной некоторым друзьям, но
никогда не публиковавшейся». В кратком введении Муавр отметил, что для
решения ряда задач теории вероятностей необходимо подсчитывать суммы членов
биномиального распределения и что вычисления становятся громоздкими при больших
значениях числа испытаний. В результате перед Муавром возник вопрос о
разыскании асимптотической формулы. Эта задача была им благополучно решена.
Основная трудность, которая при этом возникала, состояла в оценке факториала ![]() при больших значениях
при больших значениях ![]() . Муавр доказал, что
. Муавр доказал, что
![]() , где
, где ![]() , однако это его не
удовлетворило и ему хотелось связать эту константу с ранее введенными в
математику. Стирлинг показал, что
, однако это его не
удовлетворило и ему хотелось связать эту константу с ранее введенными в
математику. Стирлинг показал, что ![]() .
Известную формулу Стирлинга для приближенного вычисления факториала в
случае больших чисел, таким образом, следовало бы назвать формулой Муавра.
Использовав найденную им формулу «Стирлинга», Муавр первоначально
выяснил, что в случае
.
Известную формулу Стирлинга для приближенного вычисления факториала в
случае больших чисел, таким образом, следовало бы назвать формулой Муавра.
Использовав найденную им формулу «Стирлинга», Муавр первоначально
выяснил, что в случае ![]() средний член
бинома
средний член
бинома ![]() асимптотически равен
асимптотически равен ![]() , а затем доказал локальную
теорему, названную его именем. Далее Муавр получил локальную теорему для
случая
, а затем доказал локальную
теорему, названную его именем. Далее Муавр получил локальную теорему для
случая ![]() фактически в принятом
теперь виде.
фактически в принятом
теперь виде.
Имея в руках локальную теорему, Муавр без затруднений сформулировал и интегральную, правда, только для симметричных границ.
Муавр отметил, что
интегральную теорему можно использовать и для оценки неизвестной вероятности ![]() , т.е. для решения обратной
задачи, задачи математической статистики.
, т.е. для решения обратной
задачи, задачи математической статистики.
11. Контроль качества продукции
В связи с переходом промышленности на массовое изготовление изделий, резко увеличился интерес к проверке качества изделий, входящих в принимаемую партию. Появилась глубокая по содержанию и значительная по своим практическим применениям теория статистических методов приемочного контроля, основанная на широком использовании теории вероятностей.
Первым шагом,
относящимся к этому кругу идей, следует считать одну из задач, рассмотренных Т. Симпсоном
в книге «Природа и законы случая» (1740 г.). Имеется данное число вещей
различного сорта ![]() вещей первого,
вещей первого, ![]() второго и т.д. Наудачу
дерутся
второго и т.д. Наудачу
дерутся ![]() вещей. Найти вероятность
того, что при этом будет взято
вещей. Найти вероятность
того, что при этом будет взято ![]() вещей
первого сорта,
вещей
первого сорта, ![]() второго и т.д.
второго и т.д.
Спустя сто с небольшим лет, к этой задаче вновь вернулся М.В. Остроградский (1801–1862) в работе «Об одном вопросе, касающемся вероятностей» (1846). Он вычислил необходимые для практического применения таблицы. Приведем подлинные слова Остроградского. «В сосуде имеются белые и черные шары, общее количество которых нам известно, но мы не знаем, сколько из них какого цвета. Мы извлекаем некоторое количество шаров, подсчитав, сколько из них белых и сколько черных, снова кладем в сосуд. Требуется определить вероятность того, что общее число белых не выходит из наперед заданных пределов. Или, лучше сказать, мы ищем зависимость между этой вероятностью и пределами, о которых идет речь.
Чтобы понять важность этого вопроса, представим себя на месте того, кто должен получить большое число предметов, причем должны выполняться некоторые условия, и кто, чтобы проверить эти условия, должен на каждый предмет потратить некоторое время. Перед армейскими поставщиками часто стоят такого рода задачи. Для них шары, содержащиеся в сосуде, представляют получаемые предметы, белые, например предметы приемлемые, как удовлетворяющие определенным условиям, а черные неприемлемые.
Таким образом, если бы вопрос, который мы перед собой поставили, был решен, поставщик мог бы воспользоваться этим, чтобы свести приблизительно к двадцатой доле часто очень утомительную механическую работу, как, например, проверку большого количества мешков муки или штук сукна».
Общее число шаров в урне известно, но неизвестен ее состав. Его и следует оценить при выборке, взятой из урны наудачу. Для этой цели Остроградский использует формулы Байеса.
Статистические методы приемочного контроля получили особенно бурное развитие в годы Второй мировой войны, поскольку было необходимо принимать огромные партии однородной продукции, а проверять ее сплошь не было возможностей по ряду причин. Нет возможности здесь перечислить даже основные этапы развития теории статистических методов приемочного контроля. Большое число исследователей работали над различными проблемами этой тематики и внесли в ее развитие крупный вклад. Из отечественных ученых заслуживают быть отмеченными А.Н. Колмогоров, В.И. Романовский, С.Х. Сираждинов, Ю.К. Беляев и др.
12. Развитие теории ошибок наблюдений
Уже упоминалось, что Галилей заложил основы теории ошибок измерений и ввел в рассмотрение ряд важных понятий, которые сохранили значение и в наши дни.
Позднее под влиянием в первую очередь астрономических и геодезических наблюдений интерес к ошибкам измерений значительно возрос. Знаменитый астроном-наблюдатель Тихо Браге (1546–1601) обратил внимание на то, что каждое отдельное измерение несет в себе возможную ошибку и точность измерений значительно повышается, если произвести несколько измерений и взять из них среднее арифметическое.
Казалось бы, от И. Кеплера (1571–1630), сделавшего так много для формирования законов движения планет, следовало ожидать повышенного внимания к методам обработки результатов наблюдений. Но эти вопросы фактически остались в стороне от его интересов, и он заметил только то, что хороший наблюдатель производит измерения с ошибками ограниченной величины.
Первые попытки построить математическую теорию ошибок измерений принадлежат Р. Котсу (1682–1716), Т. Симпсону (1710–1761) и Д. Бернулли (1700–1782).
Позднее теория ошибок измерений привлекла внимание практически всех видных специалистов в области теории вероятностей. Она оказала серьезное влияние на постановку задач и разработку методов математической статистики.
13. Формирование понятия случайной величины
Ведение понятия случайной величины связано с именами многих ученых, которые хотя и не использовали этого термина, но фактически исследовали отдельные его свойства.
Начиная с Котса, Симпсона и Н. Бернулли в 18-ом веке начала развиваться теория ошибок наблюдений, возникшая в первую очередь под влиянием астрономии. Ошибка измерения в зависимости от случая может принимать различные значения. Эта позиция была высказана Галилеем задолго до работ упомянутых ученых. Он же ввел в обиход термин «случайная» и «систематическая ошибка» измерения. Вторая тесно связана с качеством изготовления прибора, мастерством наблюдателя, условиями наблюдения. Первая же зависит от многочисленных причин, влияние которых невозможно учесть и которые изменяются от наблюдения к наблюдению. Теперь мы ясно видим, что ошибка измерения представляет собой случайную величину с каким-то неизвестным нам распределением вероятностей.
Но с понятием
случайной величины встречались уже Я. Бернулли, Н. Бернулли,
Монмор, Муавр. В самом деле, Я. Бернулли рассмотрел число
появлений интересующего его события в ![]() независимых
испытаниях. Для нас теперь это случайная величина, способная принимать значения
независимых
испытаниях. Для нас теперь это случайная величина, способная принимать значения
![]() с вероятностями,
задаваемыми формулами Бернулли. Н. Бернулли, Монмор и Муавр,
исследуя задачу о разорении игрока, также имели дело со случайной величиной:
числом партий, которые необходимы для разорения. Муавр пошел еще дальше,
он ввел в рассмотрение нормальное распределение вероятностей. Однако никто из
перечисленных ученых не заметил, что в науку властно постучалась необходимость
введения нового понятия случайной величины.
с вероятностями,
задаваемыми формулами Бернулли. Н. Бернулли, Монмор и Муавр,
исследуя задачу о разорении игрока, также имели дело со случайной величиной:
числом партий, которые необходимы для разорения. Муавр пошел еще дальше,
он ввел в рассмотрение нормальное распределение вероятностей. Однако никто из
перечисленных ученых не заметил, что в науку властно постучалась необходимость
введения нового понятия случайной величины.
Первоначально считалось, что возможные значения ошибок измерений составляют арифметическую прогрессию с неопределенной, но очень малой разностью. Затем постепенно от этого предположения отказались и стали представлять себе, что возможные значения, принимаемые ошибками наблюдений, заполняют целый отрезок, вероятности возможных значений определялись посредством плотности распределения. И если Д. Бернулли в отношении плотности распределения вероятностей допускал еще определенные вольности, то у Лапласа, Гаусса, Лежандра с плотностью распределения уже было все в порядке. Это была неотрицательная функция, интеграл которой по всей прямой равен 1, а вероятность попадания в тот или иной отрезок равнялся интегралу от плотности, взятому по этому отрезку. Лапласу уже была известна формула для разыскания плотности распределения суммы по плотностям распределения слагаемых. В книге «Аналитическая теория вероятностей» Лаплас умело оперирует с плотностями распределения, ставит и решает ряд интересных задач, но нигде не вводит понятия случайной величины. Он либо использует язык теории ошибок измерений, либо язык математического анализа и не ощущает потребности в новом понятии теории вероятностей.
Первая половина 19-го века принесла новые задачи, которые нуждаются в понятии случайной величины. Прежде всего, это исследования бельгийского естествоиспытателя А. Кетле (1796–1874), заметившего, что размеры органов животных определенного возраста подчиняются нормальному распределению. Изучение уклонений снаряда от цели явилось предметом исследования многих ученых; они также пришли к выводу о нормальном распределении этой величины.
Многочисленные
исследования многих крупных математиков подготовили почву для введения понятия
случайной величины. По-видимому, первый шаг был сделан Пуассоном в
мемуаре 1832 г. «О вероятности средних результатов наблюдений». Термина
случайная величина у Пуассона еще нет, но он пишет о «некоторой вещи»,
которая способна принять значения ![]() соответственно
с вероятностями
соответственно
с вероятностями ![]() . Он рассмотрел
также непрерывные случайные величины и их плотности распределения.
. Он рассмотрел
также непрерывные случайные величины и их плотности распределения.
Итак, Пуассоном был сделан важный шаг в науке, он ввел в научный обиход новое понятие – случайную величину. Его первоначальный термин «вещь» не привился и вскоре перестал употребляться. Чебышев в своих мемуарах по теории вероятностей уже использует термин «величина» и автоматически считает все случайные величины, с которыми имеет дело, независимыми. В работе же Ляпунова по теории вероятностей систематически используется термин «случайная величина» и всюду, где это необходимо, оговаривается, что автор имеет дело с независимыми случайными величинами.
Определение случайной величины, данное Пуассоном, теперь уже не может считаться математическим. Это скорее описание реального объекта изучения, обращение к интуиции, полученной в результате научного и житейского опыта. Даже несложный логический анализ этого определения показывает, что из него совсем не следуют правила для действий над случайными величинами. Для того, чтобы случайная величина приобрела статус полноценного математического понятия, ей необходимо дать строго формализованное определение. Это было сделано в конце 20-х годов А.Н. Колмогоровым в небольшой статье, посвященной аксиоматике теории вероятностей, а затем в подробностях изложено в его знаменитой книге «Основные понятия теории вероятностей». Подход Колмогорова стал теперь общепринятым, поскольку он полноценно включил теорию вероятностей в общий стиль современного изложения, принятый в математике.
14. Закон больших чисел
Знаменитая
теорема Я. Бернулли о сближении при увеличении числа наблюдений
вероятности события ![]() с частотой его
появления получила первое обобщение лишь в 1837 г. в работе Пуассона
«Исследования о вероятностях в решении судебных дел уголовных и гражданских».
Именно в этом мемуаре он ввел сам термин «закон больших чисел». Но его
результаты не внесли в теорию вероятностей существенного прогресса, поскольку в
идейном плане они не выходили за пределы концепции Я. Бернулли.
Существенный сдвиг в этом направлении связан с работой Чебышева «О средних
величинах» (1867). В этой работе он перешел от рассмотрения случайных событий к
случайным величинам. Теорема Чебышева теперь излагается во всех
учебниках теории вероятностей. Она неоднократно позднее служила источником
обобщений.
с частотой его
появления получила первое обобщение лишь в 1837 г. в работе Пуассона
«Исследования о вероятностях в решении судебных дел уголовных и гражданских».
Именно в этом мемуаре он ввел сам термин «закон больших чисел». Но его
результаты не внесли в теорию вероятностей существенного прогресса, поскольку в
идейном плане они не выходили за пределы концепции Я. Бернулли.
Существенный сдвиг в этом направлении связан с работой Чебышева «О средних
величинах» (1867). В этой работе он перешел от рассмотрения случайных событий к
случайным величинам. Теорема Чебышева теперь излагается во всех
учебниках теории вероятностей. Она неоднократно позднее служила источником
обобщений.
В 1909 г.
Э. Борель для ![]() показал,
что в случае схемы Бернулли имеет место более сильное предложение, чем закон
больших чисел. Именно, он доказал, а в 1917 г. это предложение на
произвольное
показал,
что в случае схемы Бернулли имеет место более сильное предложение, чем закон
больших чисел. Именно, он доказал, а в 1917 г. это предложение на
произвольное ![]() распространил итальянский
математик Кантелли, что
распространил итальянский
математик Кантелли, что ![]() .
.
Это предложение получило наименование усиленного закона больших чисел. Широкое обобщение усиленного закона больших чисел было дано Колмогоровым в работе 1930 г., а также в 1934 г. в его монографии «Основные понятия теории вероятностей».
В 1935 г.
Хинчин ввел новое понятие относительной устойчивости сумм, которое
должно было дать максимально общую форму закона больших чисел для положительных
случайных величин. Пусть ![]() последовательность
неотрицательных случайных величин. Про суммы
последовательность
неотрицательных случайных величин. Про суммы ![]() говорят,
что они относительно устойчивы, если можно найти такие положительные константы
говорят,
что они относительно устойчивы, если можно найти такие положительные константы ![]() , что при
, что при ![]() выполнено соотношение
выполнено соотношение 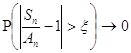 .
.
В случае
одинаково распределенных величин ![]() Хинчину
удалось найти необходимое и достаточное условие для относительной
устойчивости сумм
Хинчину
удалось найти необходимое и достаточное условие для относительной
устойчивости сумм ![]() . Ученик Хинчина А.А. Бобров
распространил этот результат на случай разнораспределенных слагаемых.
. Ученик Хинчина А.А. Бобров
распространил этот результат на случай разнораспределенных слагаемых.
Существенное расширение проблематики, связанной с законом больших чисел, было осуществлено В.И. Гливенко в работах, относящихся к 1929–1933 гг., когда он начал рассматривать предельные теоремы для случайных величин со значениями в функциональных пространствах. Вершиной его результатов является замечательная теорема о сходимости эмпирических распределений к истинной функции распределения наблюдаемой случайной величины. Теорема Гливенко, сразу же после ее опубликования, была названа Кантелли основной теоремой математической статистики.
15. Центральная предельная теорема
Теорема Муавра
о сходимости распределений центрированного и нормированного числа появлений
события ![]() в
в ![]() независимых испытаниях, в
каждом из которых событие
независимых испытаниях, в
каждом из которых событие ![]() может
наступить с одной и той же вероятностью
может
наступить с одной и той же вероятностью ![]() ,
к нормальному распределению долгое время служила образцом для последующих
обобщений. Первое обобщение принадлежит Лапласу и уже формулируется как
предельная теорема для сумм независимых случайных величин
,
к нормальному распределению долгое время служила образцом для последующих
обобщений. Первое обобщение принадлежит Лапласу и уже формулируется как
предельная теорема для сумм независимых случайных величин ![]() , каждая из которых
равномерно распределена на отрезке
, каждая из которых
равномерно распределена на отрезке ![]() . Лаплас
рассматривал дискретные случайные величины с увеличивающимся числом возможных
значений. Этим самым давалась аппроксимация непрерывного распределения
дискретным.
. Лаплас
рассматривал дискретные случайные величины с увеличивающимся числом возможных
значений. Этим самым давалась аппроксимация непрерывного распределения
дискретным.
Существенное
продвижение исследований по предельной теореме связано с именем Пуассона.
Он рассмотрел схему последовательности независимых испытаний с разными
вероятностями появления события ![]() в
каждом из испытаний. Пуассон доказал для этого случая локальную теорему.
здесь же он дал ошибочное обобщение этой теоремы на суммы произвольных
независимых случайных величин, имеющих конечные дисперсии, при условии их
центрирования суммами математических ожиданий и нормирования квадратным корнем
из суммы дисперсий слагаемых.
в
каждом из испытаний. Пуассон доказал для этого случая локальную теорему.
здесь же он дал ошибочное обобщение этой теоремы на суммы произвольных
независимых случайных величин, имеющих конечные дисперсии, при условии их
центрирования суммами математических ожиданий и нормирования квадратным корнем
из суммы дисперсий слагаемых.
Интерес к нормальному распределению в начале 19-го века возрос в связи с появлением знаменитых исследований Лежандра и Гаусса по формулировке и обоснованию метода наименьших квадратов.
Второй толчок, который вызвал дополнительный интерес к предельным теоремам теории вероятностей, была статистическая физика, начала которой были построены в середине 19-го века. Первый общий результат в этом направлении был сформулирован в 1887 г. Чебышевым. Для доказательства этого предложения Чебышевым был разработан весьма сильный метод, получивший название метода моментов и являющийся одним из крупнейших достижений науки того времени. Однако, в формулировке теоремы и ее доказательстве был допущен ряд промахов, которые сразу же взялся исправлять ученик Чебышева А.А. Марков. Им была строго доказана несколько исправленная теорема Чебышева. Ляпунов на протяжении 1900–1901 гг. обобщил полученные результаты.
Общность результатов Ляпунова произвела огромное впечатление на современников. Именно в ту пору появился термин «центральная предельная теорема» для обозначения условной сходимости функций распределения нормированных и центрированных математическими ожиданиями сумм к нормальному распределению.
Многие ученые занимались и добились некоторых результатов при изучении центральной предельной теоремы: Линдеберг (1922), Феллер (1934), Бернштейн (1927), Хинчин и Леви (1935)…
Исследование вопроса сходимости функции распределения к нормальному закону не окончились и в наши дни.
16. Общие предельные распределения для сумм
Естественный вопрос о том, какие распределения возможны в качестве предельных для сумм независимых случайных величин при условии, что они примерно одинаковы по величине, возник только в двадцатые-тридцатые годы 20-го века. Этот вопрос подробно исследовали Колмогоров, Гнеденко, Леви, Хинчин.
17. Формирование понятий математического ожидания и дисперсии
Понятие
математического ожидания в самых начальных его элементах было введено в теорию
вероятностей очень рано: впервые оно появилось в переписке Паскаля и Ферма.
В более явной форме оно было введено Гюйгенсом. Но в ту пору этому
термину придавался смысл ожидания той средней цены, которую можно дать за
приобретение случайной величины, дающей выигрыш ![]() с
вероятностью
с
вероятностью ![]() .
.
Для 18-го века обращение к математическому ожиданию было не характерным. Все внимание привлекало понятие вероятности случайного события. В знаменитой книге Лапласа «Аналитическая теория вероятностей» нет определения математического ожидания и тем более правил действия с ними. Возможно, это связано с тем, что Лаплас не рассматривал и понятия случайной величины, вместо этого он изучал ошибки наблюдений, плотности их распределений и даже вывел, и использовал формулу для плотности суммы двух независимых ошибок.
Казалось бы, создание и развитие теории ошибок наблюдений должно было стимулировать изучение числовых характеристик случайных величин. Однако этого не случилось. Впрочем, для нормального распределения были введены понятия истинного значения и точности наблюдений; было известно, как их вычислять по плотности распределения. Таким образом, для этого частного случая уже была известна формула для вычисления математического ожидания и дисперсии.
В начале 19-го века нормальное распределение затмило собой все остальные, поскольку с ним столкнулись в теории ошибок наблюдений и, казалось, доказали в работах Гаусса и Лежандра, что распределение ошибок наблюдений должно быть нормальным. Остальные распределения потеряли интерес, о них попросту не думали. Несомненно, в связи с этим никто не помышлял о доказательстве теорем относительно математических ожиданий и дисперсий, поскольку для нормального распределения уже было все известно. Заметим, что в книге Чебышева «Опыт элементарного анализа теории вероятностей» понятия случайной величины, математического ожидания и дисперсии даже не упоминаются. Однако в курсе лекций по теории вероятностей, которые систематически он читал в Петербургском университете, Чебышев говорит о величинах (имея в виду случайные величины), их математическом ожидании и дисперсии. Более того, в этих лекциях было сказано, что «оно (понятие математического ожидания) имеет большее значение на практике, чем сама вероятность, потому что на основании ее у нас составляется суждение о том, что мы можем ожидать перед появлением известного события».
В этих лекциях имеется доказательство и формулировка теорем о математическом ожидании и дисперсии суммы случайных величин. Там же он привел и вывод своего знаменитого неравенства. При этом он предполагал как нечто самоочевидное, что речь идет о независимых величинах.
Только в учебнике «Исчисление вероятностей» (1913–1924) строго доказываются и теорема о математическом ожидании произведения и о математическом ожидании суммы со специальным упоминанием о том, что она верна не только для независимых величин.
Понятие случайного процесса принадлежит прошлому столетию и связано с именами Колмогорова, Хинчина, Слуцкого, Винера (1894–1965). Это понятие в наши дни является одним из центральных не только в теории вероятностей, но также в естествознании, инженерном деле, экономике, организации производства, теории связи. Теория случайных процессов принадлежит к категории наиболее быстро развивающихся математических дисциплин. Несомненно, что это обстоятельство в значительной мере определяется ее глубокими связями с практикой.
20-ый век не мог удовлетвориться тем идейным наследием, которое было получено им от прошлого. В то время, как физика, инженера, биолога интересовал процесс, т.е. изменение изучаемого явления во времени, теория вероятностей предлагала им в качестве математического аппарата лишь средства, изучавшие стационарные состояния. Для исследования изменения во времени теория вероятностей конца 19-го начала 20-го века не имела ни разработанных частных схем, ни тем более общих приемов. Изучение броуновского движения в физике подвело математику к порогу создания теории случайных процессов. В исследованиях датского ученого А.К. Эрланга была начата новая важная область поисков, связанная с изучением загрузки телефонных сетей. Число абонентов изменяется во времени случайно, а длительности каждого разговора обладает большой индивидуальностью. И вот в этих условиях двойной случайности следует производить расчет пропускной способности телефонных сетей, коммутационной аппаратуры и управляющих связью систем. Работы Эрланга оказали значительное влияние не только на решение чисто телефонных задач, но и на формирование элементов теории случайных процессов, в частности, процессов гибели и размножения.
Во втором десятилетии двадцатого века начались исследования динамики биологических популяций. Итальянский математик Вито Вольтера разработал математическую теорию этого процесса на базе чисто детерминистских соображений. Позднее ряд биологов и математиков развивали его идеи уже на основе стохастических представлений. Первоначально и в этой теории применялись исключительно идеи процессов гибели и размножения.
Теория броуновского движения, исходящая из теоретико-вероятностных предпосылок, была разработана в 1905 г. двумя известными физиками М. Смолуховским (1872–1917) и А. Эйнштейном (1879–1955). Позднее высказанные ими идеи использовались неоднократно как при изучении физических явлений, так и в различных инженерных задачах.
Попытка изучения средствами теории вероятностей явления диффузии была предпринята в 1914 г. двумя известными физиками Н. Планком (1858–1947) и Фоккером.
Мы должны упомянуть еще о двух важных группах исследований, начатых в разное время и по разным поводам. Во-первых, это работы А.А. Маркова (1856–1922) по изучению цепных зависимостей. Во-вторых, работах Е.Е. Слуцкого (1880–1948) по теории случайных функций. Оба эти направления играли очень существенную роль в формировании общей теории случайных процессов.
В 1931 г. была опубликована большая статья Колмогорова «Об аналитических методах в теории вероятностей», а через три года работа Хинчина «Теория корреляции стационарных стохастических процессов», которые следует считать началом построения общей теории случайных процессов. В первой из этих работ были заложены основы теории марковских процессов, а во второй – основы стационарных процессов. Они были источником огромного числа последующих исследований.
Обе упомянутые основополагающие работы содержат не только математические результаты, но и глубокий философский анализ причин, послуживших исходным пунктом для построения основ теории случайных процессов.
Но не общефилософское содержание является основным достоинством работы Колмогорова. В ней были заложены основы теории случайных процессов без последействия и получены дифференциальные уравнения (прямые и обратные), которые управляют вероятностями перехода. В этой же работе был дан набросок теории скачкообразных процессов без последействия, подробное развитие которой позднее было дано Феллером и Дубровским.
Построение другого класса случайных процессов на базе физических задач было осуществлено Хинчиным. Он ввел понятие стационарного процесса в широком и узком смысле и получил знаменитую формулу для коэффициента автокорреляций. Эта работа послужила основанием для последующих исследований Крамера, Вальда, Колмогорова и многих других ученых.
Заключение
В истории каждой науки постоянно приходится сталкиваться с такими ситуациями, когда эта наука еще не создана, а исследователи рассматривают отдельные задачи, которые относятся к ее компетенции. С таким же положением мы сталкиваемся и в теории случайных процессов. Этой теории еще не было, не было и свойственных ей понятий, не было даже идеи рассмотрения изменения случайной величины во времени, а отдельные задачи в этом направлении уже изучались.
Теория вероятностей имеет богатую и поучительную историю. Она наглядно показывает как возникали ее основные понятия и развивались методы из задач, с которыми сталкивался общественный прогресс. При этом мы увидим, как человечество переходило от первичных догадок к более полному и совершенному знанию, как создание теории вероятностей позволяло переходить от строгих детерминистических представлений к более широким стохастическим концепциям, тем самым, открывая новые возможности для глубоких заключений о природе вещей.
Теория вероятностей продолжает бурно развиваться, в ней появляются новые направления исследований. Эти направления представляют значительный общетеоретический и прикладной интерес.
| Методика обучения элементам теории вероятностей на факультативных ... | |
|
Введение Глава I. Вероятностно - статистическая линия в базовом школьном курсе математики 1.1 Статистическое мышление и школьное математическое ... Ответы, предложенные паскалем, таковы: первый игрок должен получить 56 пистолей, а второй - 8. рассуждения при решении подобны тем, которые были проведены при решении предыдущей ... Например, если много разбросать монету, относительная частота появления герба приближается к; при многократном бросании игральной кости частота появления грани с пятью очками ... |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Математические игры как средство развития познавательного интереса ... | |
|
Содержание Введение. 4 Глава I. Формирование познавательного интереса учащихся. 7 §1 Психолого-педагогические основы познавательного интереса. 7 §2 ... В "Математическом казино" ученик бросает кости только после решения задачи, тем самым, определяя свои выигранные баллы. В игре "Математическое (или чертово) колесо" игроки двигаются как бы по кругу, в котором имеется начальный и конечный этап, бросая кости, они тем самым определяют, на какой этап ... |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Теория вероятностей и математическая статистика | |
|
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования "Южный ... Курс "Теория вероятностей и математическая статистика" - общеобразовательная математическая дисциплина, объектом изучения которой является большая область математики, связанная ... Теорема Бернулли утверждает, что при неограниченном увеличении числа испытаний с вероятностью близкой к единице, то есть практически достоверно, можно утверждать, значения ... |
Раздел: Рефераты по математике Тип: учебное пособие |
| Серьёзные лекции по высшей экономической математике | |
|
Комбинаторные задачи. 1.Сколькими способами колода в 52 карты может быть роздана 13-ти игрокам так, чтобы каждый игрок получил по одной карте каждой ... По формуле Бернулли рассчитывается вероятность появления события A "x"раз в n повторных независимых испытаниях, где p - вероятность появления события A в одном испытании, q ... Таким образом, каждому исходу случайного эксперимента, заключающегося в серии из n испытаний по схеме Бернулли, соответствует определенное число x, рассматриваемое как случайная ... |
Раздел: Рефераты по математике Тип: реферат |
| Теория вероятности и мат статистика | |
|
Киевский политехнический институт Кафедра КСОИУ Конспект лекций по курсу: "Теория вероятности и математическая статистика" Преподаватель: Студент II ... n испытаний называются системой испытаний Бернулли, если испытания независимы, в каждом из них происходит событие , либо с вероятностью наступления P(A) = p; Теорема 1. Математическое ожидание суммы случайных величин равно сумме математических ожиданий |
Раздел: Рефераты по математике Тип: реферат |