Контрольная работа: Теория вероятности и математическая статистика. Задачи

Задача на условную вероятность.

В урне находятся 3 белых и 2 черных шара. Вынимаются 2 шара.

Найти вероятность, что оба шара белые.

А₁ - белый шар

А₂ - белый шар

P(A₁A₂)=?

C=A₁A₂

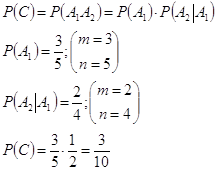
Если первый шар возвращается в урну.

P(A₁)=P(A₂)

Задача на подсчет вероятностей

Мишень состоит из 4 зон, производится один выстрел.

Найти вероятность промоха, если вероятность попадание в зоны известна и равна:

P₁=0,1

P₂=0,15

P₃=0,20

P₄=0,25

A - попадание в мишень.

- промах.

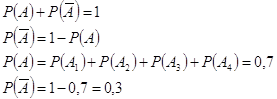
Задача на формулу полной вероятности.

Имеется 3 урны.

В одной 2 белых и 1 черный шар

Во второй 1 белый и 1 черный шар.

В третьей 3 белых и 2 черных шара.

Выбирается одна из урн и из нее 1 шар. Какова вероятность, что шар черный?

А - черный шар. P(A)=?

n=10 m=4           

Второй способ через формулу полной вероятности.

H₁; H₂; H₃;

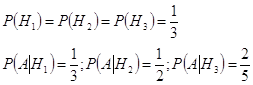
Задача на теорему о повторении опытов.

Проводят 4 независимых опыта. Вероятность события в каждом из опыте равна 0,3

Построить ряд и многогранник числа событий.

Введем Х-число появлений событий в результате проведенных опытов.

X=X₀=0

X=X₁=1

X=X₂=2

X=X₃=3

X=X₄=4

 - теорема о повторении опытов.

P0,4=1*1*0,7⁴=0,0024

P1,4=*0,3¹*0,7³=0,588

P2,4=*0,3²*0,7²=

P3,4=*0,3³*0,7¹=

P4,4=*0,3⁴*0,7⁰=

Задача на умножение вероятностей.

В урне находятся 3 белых и 2 черных шара. Вынимают по очереди 2 шара, причем первый обратно возвращают.

Какова вероятность что будут вынуты оба черных шара?

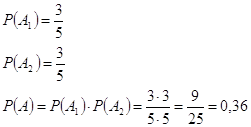
Задача на умножение вероятностей.

В урне находится 3 белых и 2 черных шара. Вынимается по 2 шара.

Найти вероятность того, что оба шара белые?

А₁ - первый шар белый.

А₂ - второй шар белый.

А=А₁А₂

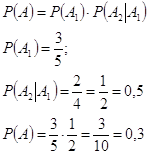
Задача на не совместные события.

Мишень состоит из 2-х зон, при одном выстреле вероятность попадания в зону 1=0,2, в зону 2=0,4

Найти вероятность промаха?

- попадание.

- промах.

А=А₁+А₂;   P(A)=P(A₁)+P(A₂)-P(A₁A₂);   P(A₁A₂)=0

Задача на схему случаев

В урне 3 белых и 4 черных шара. Какова вероятность изъятия из урны трех черных шаров?

n - общее число возможных случаев изъятия 3 шаров из урны.

m - число благоприятных случаев. (все три шара черные)

,