Контрольная работа: Теория информации. Статистический подход
МОСКОВСКИЙ ГУМАНИТАРНО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ
Калужский филиал
Юридический факультет
Кафедра гражданско-правовых дисциплин
Контрольная работа
по учебному курсу
"Математические методы анализа и принятия решений"
Выполнил: Титов Е.А.
студент 4-го курса
группа ЮЗВС-08
Руководитель:
Махмудов Н.Р.
Калуга - 2010 г.
План
Статистический подход к измерению правовой информации
Графический метод решения задач линейного программирования
Методика решения задач ЛП графическим методом
Список используемой литературы
Статистический подход к измерению правовой информации
Статистический подход изучается в разделе кибернетики, называемом теорией информации. Его основоположником считается К. Шеннон, опубликовавший в 1948 году свою математическую теорию связи. Большой вклад в теорию информации до него внесли ученые Найквист и Хартли.
В 1924 и 1928 гг. они опубликовали работы по теории телеграфии и передаче информации. Признаны во всем мире исследования по теории информации российских ученых А.Н. Колмогорова, А.Я. Хинчина, В.А. Котельникова, А.А. Харкевича и др.
К. Шенноном было введено понятие количество информации как меры неопределенности состояния системы, снимаемой при получении информации.
Количественно выраженная неопределенность состояния получила название энтропии по аналогии с подобным понятием в статистической механике.
При получении информации уменьшается неопределенность, т.е. энтропия, системы. Очевидно, что чем больше информации получает наблюдатель, тем больше снимается неопределенность, и энтропия системы уменьшается.
При энтропии, равной нулю, о системе имеется полной информация, и наблюдателю она представляется целиком упорядоченной. Таким образом, получение информации связано с изменением степени неосведомленности получателя о состоянии этой системы.
До получения информации ее получатель мог иметь некоторые предварительные (априорные) сведения о системе Х.
Оставшаяся неосведомленность и является для него мерой неопределенности состояния (энтропией) системы. Обозначим априорную энтропию системы Х.
После получения некоторого сообщения наблюдатель приобрел дополнительную информацию уменьшившую его начальную неосведомленность.
Другими словами, количество информации измеряется уменьшением (изменением) неопределенности состояния системы.
Вероятность p - количественная априорная (т.е. известная до проведения опыта) характеристика одного из исходов (событий) некоторого опыта. Измеряется в пределах от 0 до 1.
Если заранее известны все исходы опыта, сумма их вероятностей равна 1, а сами исходы составляют полную группу событий.
Если все исходы могут свершиться с одинаковой долей вероятности, они называются равновероятными.
Например, пусть опыт состоит в сдаче студентом экзамена по информатике.
Очевидно, у этого опыта всего 4 исхода (по количеству возможных оценок, которые студент может получить на экзамене).
Тогда эти исходы составляют полную группу событий, т.е. сумма их вероятностей равна 1. Если студент учился хорошо в течение семестра, значения вероятностей всех исходов могут быть такими:
p (5) = 0.5; p (4) = 0.3; p (3) = 0.1; p (2) = 0.1, где запись p (j) означает вероятность исхода, когда получена оценка j (j = {2, 3, 4, 5}).
Если студент учился плохо, можно заранее оценить возможные исходы сдачи экзамена, т.е. задать вероятности исходов, например, следующим образом: p (5) = 0.1; p (4) = 0.2; p (3) = 0.4; p (2) = 0.3.
В обоих случаях выполняется условие:
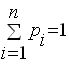
где n - число исходов опыта,
i - номер одного из исходов.
Пусть можно получить n сообщений по результатам некоторого опыта (т.е. у опыта есть n исходов), причем известны вероятности получения каждого сообщения (исхода) - pi.
Тогда в соответствии с идеей Шеннона, количество информации I в сообщении i определяется по формуле:
I = - log2 pi,
где pi - вероятность i-го сообщения (исхода).
Пример 1. Определить количество информации, содержащейся в сообщении о результате сдачи экзамена для студента-хорошиста.
Пусть I (j) - количество информации в сообщении о получении оценки j. В соответствии с формулой Шеннона имеем:
I (5) = - log2 0,5 = 1,I (4) = - log2 0,3 = 1,74,I (3) = - log2 0,1 = 3,32
I (2) = - log2 0,1 = 3,32.
Пример 2. Определить количество информации, содержащейся в сообщении о результате сдачи экзамена для нерадивого студента:
I (5) = - log2 0,1 = 3,32,I (4) = - log2 0,2 = 2,32,I (3) = - log2 0,4 = 1,32,I (2) = - log2 0,3 = 1,74.
Таким образом, количество получаемой с сообщением информации тем больше, чем неожиданнее данное сообщение. Этот тезис использован при эффективном кодировании кодами переменной длины (т.е. имеющими разную геометрическую меру): исходные символы, имеющие большую частоту (или вероятность), имеют код меньшей длины, т.е. несут меньше информации в геометрической мере, и наоборот.
Формула Шеннона позволяет определять также размер двоичного эффективного кода, требуемого для представления того или иного сообщения, имеющего определенную вероятность появления.
Помимо информационной оценки одного сообщения, Шеннон предложил количественную информационную оценку всех сообщений, которые можно получить по результатам проведения некоторого опыта. Так, среднее количество информации Iср, получаемой со всеми n сообщениями, определяется по формуле:
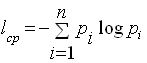
где pi - вероятность i-го сообщения.
Пример 3. Определить среднее количество информации, получаемое студентом-хорошистом, по всем результатам сдачи экзамена.
В соответствии с приведенной формулой имеем:
Iср = - (0,5*log20,5 + 0,3*log20,3 + 0,1*log20,1 + 0,1*log20,1) = 1,67.
Пример 4. Определить среднее количество информации, получаемое нерадивым студентом, по всем результатам сдачи экзамена.
В соответствии с приведенной формулой имеем:
Iср = - (0,1*log20,1 + 0,2*log20,2 + 0,4*log20,4 + 0,3*log20,3) = 1,73.
Большее количество информации, получаемое во втором случае, объясняется большей непредсказуемостью результатов: в самом деле, у хорошиста два исхода равновероятны.
Пусть у опыта два равновероятных исхода, составляющих полную группу событий, т.е. p1 = p2 = 0,5. Тогда имеем в соответствии с формулой для расчета I ср:
I ср = - (0,5*log20,5 + 0,5*log20,5) = 1.
Эта формула есть аналитическое определение бита по Шеннону: это среднее количество информации, которое содержится в двух равновероятных исходах некоторого опыта, составляющих полную группу событий.
Единица измерения информации при статистическом подходе - бит.
На практике часто вместо вероятностей используются частоты исходов. Это возможно, если опыты проводились ранее и существует определенная статистика их исходов. Так, строго говоря, в построении эффективных кодов участвуют не частоты символов, а их вероятности
Введенная количественная статистическая мера информации широко используется в теории информации для оценки собственной, взаимной, условной и других видов информации.
Графический метод решения задач линейного программирования
Теоретическое введение.
Графический метод довольно прост и нагляден для решения задач линейного программирования с двумя переменными. Он основан на геометрическом представлении допустимых решений и ЦФ задачи.
Каждое из неравенств задачи
линейного программирования определяет на координатной плоскости ![]() некоторую полуплоскость
(рис.1), а система неравенств в целом - пересечение соответствующих плоскостей.
Множество точек пересечения данных полуплоскостей называется областью
допустимых решений (ОДР.). ОДР всегда представляет собой выпуклую
фигуру, т.е. обладающую следующим свойством: если две точки А и В принадлежат
этой фигуре, то и весь отрезок АВ принадлежит ей. ОДР графически может быть
представлена выпуклым многоугольником, неограниченной выпуклой многоугольной
областью, отрезком, лучом, одной точкой. В случае несовместности системы
ограничений задачи (1) ОДР является пустым множеством.
некоторую полуплоскость
(рис.1), а система неравенств в целом - пересечение соответствующих плоскостей.
Множество точек пересечения данных полуплоскостей называется областью
допустимых решений (ОДР.). ОДР всегда представляет собой выпуклую
фигуру, т.е. обладающую следующим свойством: если две точки А и В принадлежат
этой фигуре, то и весь отрезок АВ принадлежит ей. ОДР графически может быть
представлена выпуклым многоугольником, неограниченной выпуклой многоугольной
областью, отрезком, лучом, одной точкой. В случае несовместности системы
ограничений задачи (1) ОДР является пустым множеством.
Все вышесказанное относится и к случаю, когда система ограничений (1) включает равенства, поскольку любое равенство
![]()
можно представить в виде системы двух неравенств (см. рис.1)
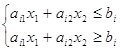
ЦФ ![]() при
фиксированном значении
при
фиксированном значении ![]() определяет на
плоскости прямую линию
определяет на
плоскости прямую линию ![]() . Изменяя
значения L, мы получим семейство параллельных прямых,
называемых линиями уровня.
. Изменяя
значения L, мы получим семейство параллельных прямых,
называемых линиями уровня.
Это связано с тем, что изменение
значения L повлечет изменение лишь длины отрезка,
отсекаемого линией уровня на оси ![]() (начальная
ордината), а угловой коэффициент прямой
(начальная
ордината), а угловой коэффициент прямой ![]() останется
постоянным (см. рис.1). Поэтому для решения будет достаточно построить одну из
линий уровня, произвольно выбрав значение L.
останется
постоянным (см. рис.1). Поэтому для решения будет достаточно построить одну из
линий уровня, произвольно выбрав значение L.
Вектор ![]() с координатами из
коэффициентов ЦФ при
с координатами из
коэффициентов ЦФ при ![]() и
и ![]() перпендикулярен к каждой
из линий уровня (см. рис.1). Направление вектора
перпендикулярен к каждой
из линий уровня (см. рис.1). Направление вектора ![]() совпадает
с направлением возрастания ЦФ, что является важным моментом для решения
задач. Направление убывания ЦФ противоположно направлению вектора
совпадает
с направлением возрастания ЦФ, что является важным моментом для решения
задач. Направление убывания ЦФ противоположно направлению вектора ![]() .
.
Суть графического метода
заключается в следующем. По направлению (против направления) вектора ![]() в ОДР производится поиск
оптимальной точки
в ОДР производится поиск
оптимальной точки ![]() . Оптимальной
считается точка, через которую проходит линия уровня
. Оптимальной
считается точка, через которую проходит линия уровня ![]() , соответствующая
наибольшему (наименьшему) значению функции
, соответствующая
наибольшему (наименьшему) значению функции ![]() .
Оптимальное решение всегда находится на границе ОДР, например, в последней
вершине многоугольника ОДР, через которую пройдет целевая прямая, или на всей
его стороне.
.
Оптимальное решение всегда находится на границе ОДР, например, в последней
вершине многоугольника ОДР, через которую пройдет целевая прямая, или на всей
его стороне.
При поиске оптимального решения задач линейного программирования возможны следующие ситуации: существует единственное решение задачи; существует бесконечное множество решений (альтернативный оптиум); ЦФ не ограничена; область допустимых решений - единственная точка; задача не имеет решений.
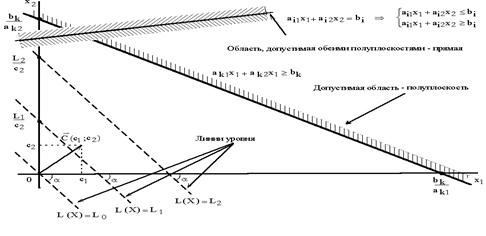
Рисунок 1. Геометрическая интерпретация ограничений и ЦФ задачи.
Методика решения задач ЛП графическим методом
В ограничениях задачи заменить знаки неравенств знаками точных равенств и построить соответствующие прямые.
Найти и заштриховать полуплоскости, разрешенные каждым из ограничений-неравенств задачи. Для этого нужно подставить в конкретное неравенство координаты какой-либо точки [например, (0; 0)], и проверить истинность полученного неравенства.
Если неравенство истинное,
то надо заштриховать полуплоскость, содержащую данную точку;
иначе (неравенство ложное) надо заштриховать полуплоскость, не содержащую данную точку.
Поскольку ![]() и
и ![]() должны быть
неотрицательными, то их допустимые значения всегда будут находиться выше оси
должны быть
неотрицательными, то их допустимые значения всегда будут находиться выше оси ![]() и правее оси
и правее оси ![]() , т.е. в I-м
квадранте.
, т.е. в I-м
квадранте.
Ограничения-равенства разрешают только те точки, которые лежат на соответствующей прямой. Поэтому необходимо выделить на графике такие прямые.
Определить ОДР как часть плоскости, принадлежащую одновременно всем разрешенным областям, и выделить ее. При отсутствии ОДР задача не имеет решений.
Если ОДР - не пустое множество,
то нужно построить целевую прямую, т.е. любую из линий уровня ![]() (где L - произвольное
число, например, кратное
(где L - произвольное
число, например, кратное ![]() и
и ![]() , т.е. удобное для проведения
расчетов). Способ построения аналогичен построению прямых ограничений.
, т.е. удобное для проведения
расчетов). Способ построения аналогичен построению прямых ограничений.
Построить вектор ![]() , который начинается в
точке (0; 0) и заканчивается в точке
, который начинается в
точке (0; 0) и заканчивается в точке ![]() . Если
целевая прямая и вектор
. Если
целевая прямая и вектор ![]() построены
верно, то они будут перпендикулярны.
построены
верно, то они будут перпендикулярны.
При поиске максимума ЦФ
необходимо передвигать целевую прямую в направлении вектора ![]() , при поиске минимума ЦФ - против
направления вектора
, при поиске минимума ЦФ - против
направления вектора ![]() . Последняя
по ходу движения вершина ОДР будет точкой максимума или минимума ЦФ. Если такой
точки (точек) не существует, то можно сделать вывод о неограниченности ЦФ на
множестве планов сверху (при поиске максимума) или снизу (при поиске
минимум).
. Последняя
по ходу движения вершина ОДР будет точкой максимума или минимума ЦФ. Если такой
точки (точек) не существует, то можно сделать вывод о неограниченности ЦФ на
множестве планов сверху (при поиске максимума) или снизу (при поиске
минимум).
Определить координаты точки max (min) ЦФ ![]() и вычислить значение ЦФ
и вычислить значение ЦФ ![]() . Для вычисления координат
оптимальной точки
. Для вычисления координат
оптимальной точки ![]() необходимо
решить систему уравнений прямых, на пересечении которых находится
необходимо
решить систему уравнений прямых, на пересечении которых находится ![]() .
.
Задача. Правоохранительные органы разработали 10 программ по борьбе с преступлениями в сфере экономики, причем среди этих программ есть одинаковые: 5 одинаковы по одним свойствам, 3 программы по другим свойствам и 2 программы одинаковы по третьим свойствам. Сколькими способами эти программы могут быть переставлены?
Ответ.5*3*2 =30
Список используемой литературы
1. Аветисян Р.Д., Аветисян Д.В. Теоретические основы информатики. - М.: РГГУ, 1997.
2. Гришкин И.И. Понятие информации. Логико-методологический аспект. - М.: Наука, 1973.
3. Дмитриев В.И. Прикладная теория информации. - М., 1989.
4. Седов Е.А. Эволюция и информация. - М.: Наука, 1976.
5. Смородинский С.С., Батин Н.В. - Оптимизация решений на основе методов.
6. Кононов В.А. - Исследование операций. Для продвинутых математиков.
7. Чернавский Д.С. Синергетика и информация. - М.: Знание, 1990.