Курсовая работа: Перебор с возвратом
Министерство образования Республики Беларусь
Учреждение образования
«Гомельский государственный университет им. Ф. Скорины»
Математический факультет
Кафедра МПУ
Курсовая работа
Перебор с возвратом
Исполнитель:
Студентка группы М-32
Ловренчук А.Ю.
Научный руководитель:
Канд. физ-мат. наук, доцент
Звягина Т.Е.
Гомель 2007
Введение
Даны N упорядоченных множеств U1, U2, ..., UN (N - известно), и требуется построить вектор A=(a1, a2, ..., aN), где a1ÎU1, a2ÎU2, ..., aNÎUN, удовлетворяющий заданному множеству условий и ограничений.
В алгоритме перебора вектор А строится покомпонентно слева направо. Предположим, что уже найдены значения первых (k-1) компонент, А=(а1, а2, ..., а(k-1), ?, ..., ?), тогда заданное множество условий ограничивает выбор следующей компоненты аk некоторым множеством SkÌUk. Если Sk<>[ ] (пустое), мы вправе выбрать в качестве аk наименьший элемент Sk и перейти к выбору (k+1) компоненты и так далее. Однако если условия таковы, что Sk оказалось пустым, то мы возвращаемся к выбору (k-1) компоненты, отбрасываем а(k-1) и выбираем в качестве нового а(k-1) тот элемент S(k-1), который непосредственно следует за только что отброшенным. Может оказаться, что для нового а(k-1) условия задачи допускают непустое Sk, и тогда мы пытаемся снова выбрать элемент аk. Если невозможно выбрать а(k-1), мы возвращаемся еще на шаг назад и выбираем новый элемент а(k-2) и так далее.
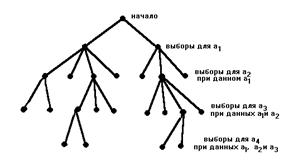
Графическое изображение - дерево поиска. Корень дерева (0 уровень) есть пустой вектор. Его сыновья суть множество кандидатов для выбора а1, и, в общем случае, узлы k-го уровня являются кандидатами на выбор аk при условии, что а1, а2, ..., а(k-1) выбраны так, как указывают предки этих узлов. Вопрос о том, имеет ли задача решение, равносилен вопросу, являются ли какие-нибудь узлы дерева решениями. Разыскивая все решения, мы хотим получить все такие узлы.
Рекурсивная схема реализации алгоритма.
procedure Backtrack(вектор,i);
begin
if <вектор является решением> then <записать его>
else begin <вычислить Si>;
for aÎSi do Backtrack(векторêêa,i+1);
{êê- добавление к вектору компоненты}
end;
end;
Оценка временной сложности алгоритма. Данная схема реализации перебора приводит к экспоненциальным алгоритмам. Действительно, пусть все решения имеют длину N, тогда исследовать требуется порядка çS1ç*çS2ç*...*çSNç узлов дерева. Если значение Si ограничено некоторой константой С, то получаем порядка СN узлов.
1. Задача о расстановке ферзей
На шахматной доске N*N требуется расставить N ферзей таким образом, чтобы ни один ферзь не атаковал другого.
Отметим следующее. Все возможные способы расстановки ферзей - СNN^2 (около 4,4*109 для N=8). Каждый столбец содержит самое большее одного ферзя, что дает только NN расстановок (1,7*107 для N=8). Никакие два ферзя нельзя поставить в одну строку, а поэтому, для того чтобы вектор (а1, а2, ..., aN) был решением, он должен быть перестановкой элементов (1, 2, ..., N), что дает только N! (4,0*104 для N=8) возможностей. Никакие два ферзя не могут находиться на одной диагонали, это сокращает число возможностей еще больше (для N=8 в дереве остается 2056 узлов). Итак, с помощью ряда наблюдений мы исключили из рассмотрения большое число возможных расстановок N ферзей на доске размером N*N. Использование подобного анализа для сокращения процесса перебора называется поиском с ограничениями или отсечением ветвей в связи с тем, что при этом удаляются поддеревья из дерева. Второе. Другим усовершенствованием является слияние, или склеивание, ветвей. Идея состоит в том, чтобы избежать выполнения дважды одной и той же работы: если два или больше поддеревьев данного дерева изоморфны, мы хотим исследовать только одно из них. В задаче о ферзях мы можем использовать склеивание, заметив, что если а1>éN/2ù, то найденное решение можно отразить и получить решение, для которого а1£éN/2ù. Следовательно, деревья, соответствующие, например, случаям а1=2 и а1=N-1, изоморфны.
Следующие рисунки иллюстрируют сказанное и поясняют ввод используемых структур данных.
|
|
|
|
Структуры данных.
Up:array[2..16] of boolean;{признак занятости диагоналей первого типа}
Down:array[-7..7] of boolean;{признак занятости диагоналей второго типа}
Vr:array[1..8] of boolean;{признак занятости вертикали}
X:array[1..8] of integer;{номер вертикали, на которой стоит ферзь на каждой горизонтали}
Далее идет объяснение “кирпичиков”, из которых “складывается” решение (технология “снизу вверх”).
procedure Hod(i,j:integer); {сделать ход}
begin
X[i]:=j;Vr[j]:=false;Up[i+j]:=false;Down[i-j]:=false;
end;
procedure O_hod(i,j:integer);{отменить ход}
begin
Vr[j]:=true;Up[i+j]:=true;Down[i-j]:=true;
end;
function D_hod(i,j:integer);
{проверка допустимости хода в позицию (i,j)}
begin
D_hod:=Vr[j]andUp[i+j]andDown[i-j];
end;
Основная процедура поиска одного варианта расстановки ферзей имеет вид:
procedure Solve(i:integer;var q:boolean);
var j:integer;
begin
j:=0;
repeat
inc(j);q:=false;{цикл по вертикали}
if D_hod(i,j) then begin Hod(i,j);
if i<8 then begin Solve(i+1,q);
if not q then O_hod(i,j);
end else q:=true;{решение найдено}
end;
until q or (j=8);
end;
Возможные модификации.
Поиск всех решений. Для доски 8*8 ответ 92.
Procedure Solve(i:integer);
var j:integer;
begin
if i<=N then begin
for j:=1 to N do if D_hod(i,j) then begin
Hod(i,j);
Solve(i+1);
O_hod(i,j);
end;
end
else begin
Inc(S);{счетчик числа решений, глобальная переменная}
Print;{вывод решения}
end;
end;
Поиск только не симметричных решений. Для доски 8*8 ответ 12.
Эта модификация требует предварительных разъяснений. Из каждого решения задачи о ферзях можно получить ряд других при помощи вращений доски на 90о, 180о и 270о и зеркальных отражений относительно линий , разделяющих доску пополам (система координат фиксирована). Доказано, что в общем случае для доски N*N (N>1) для любой допустимой расстановки N ферзей возможны три ситуации:
· при одном отражении доски возникает новая расстановка ферзей, а при поворотах и других отражениях новых решений не получается;
· новое решение при повороте на 90о и ее отражения дают еще две расстановки;
· три поворота и четыре отражения дают новые расстановки.
Для отсечения симметричных решений на всем множестве решений требуется определить некоторое отношение порядка. Представим решение в виде вектора длиной N, координатами которого являются числа от 1 до N. Для ферзя, стоящего в i-й строке, координатой его столбца является i-я координата вектора. Для того, чтобы не учитывать симметричные решения, будем определять минимальный вектор среди всех векторов, получаемых в результате симметрий. Процедуры Sim1, Sim2, Sim3 выполняют зеркальные отображения вектора решения относительно горизонтальной, вертикальной и одной из диагональных осей. Известно (из геометрии), что композиция этих симметрий дает все определенные выше симметрии шахматной доски, причем не принципиально, в какой последовательности выполняются эти процедуры для каждой конкретной композиции. Проверка «на минимальность» решения производится функцией Cmp, которая возвращает значение true в том случае, когда одно из симметричных решений строго меньше текущего.
{не лучший вариант реализации - отсечение на выводе решений}
type Tarray=array[1..N] of integer;
procedure Sim1(var X:Tarray);
var i:integer;
begin
for i:=1 to N do X[i]:=N-X[i]+1;
end;
procedure Sim2(var X:Tarray);
var i,r:integer;
begin
for i:=1 to N do begin
r:=X[i]; X[i]:=X[N-i+1];X[N-i+1]:=r;
end;
end;
procedure Sim3(var X:Tarray);
var Y:Tarray;
i:integer;
begin
for i:=1 to N do Y[X[i]]:=i;
X:=Y;
end;
function Cmp(X,Y:Tarray):boolean;
var i:integer;
begin
i:=1;
while (i<=N) and (Y[i]=X[i]) do Inc(i);
if i>N then Cmp:=false
else if Y[i]<X[i] then Cmp:=true else Cmp:=false;
end;
Procedure Solve(i:integer);
var j:integer;f:boolean;
Y:Tarray;
begin
if i<=N then begin
for j:=1 to N do if D_hod(i,j) then begin
Hod(i,j);
Solve(i+1);
O_hod(i,j);
end;
end
else begin
f:=true;
for j:=0 to 7 do begin
Y:=X;
if j and 1 =0 then Sim1(Y);
if j and 2 =0 then Sim2(Y);
if j and 4 =0 then Sim3(Y);
if Cmp(Y,X) then f:=false;
end;
if f then begin
Inc(S);{счетчик числа решений, глобальная переменная}
Print;{вывод решения}
end;
end;
end;
2. Задача о шахматном коне
Существуют способы обойти шахматным конем доску, побывав на каждом поле по одному разу. Составить программу подсчета числа способов обхода.
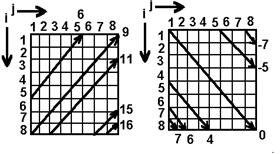
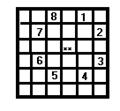
Разбор задачи начинается с оценки числа 64! - таково общее число способов разметки доски 8*8. Каждую разметку следует оценивать на предмет того, является ли она способом обхода конем доски(решение в “лоб”). Затем оцениваем порядок сокращения перебора исходя из условия - логика выбора очередного хода коня. Будем считать, что поля для хода выбираются по часовой стрелке. Объяснение иллюстрируется следующими рисунками.
|
|
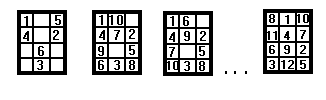
Структуры данных.
Const N= ; M= ;
Dx:array[1..8] of integer=(-2,-1,1,2,2,1,-1-2);
Dy:array[1..8] of integer=(1,2,2,1,-1,-2,-2,-1);
Var A:array[-1..N+2,-1..M+2] of integer;
Основной фрагмент реализации - процедура Solve.
procedure Solve(x,y,l:integer);
var z,i,j:integer;
begin
A[x,y]:=l;
if l=N*M then Inc(t)
else for z:=1 to 8 do begin i:=x+Dx[z];j:=y+Dy[z];
if A[i,j]=0 then Rec(i,j,l+1)
end;
A[x,y]:=0;
end;
for i:=-1 to N+2 do for j:=-1 to M do A[i,j]:=-1;
for i:=1 to N do for j:=1 to M do A[i,j]:=0;
t:=0;
for i:=1 to N do for j:=1 to M do Solve(i,j,1);
writeln(‘число способов обхода конем доски’,N,’*’,M,’--’,t);
Изменим логику так, чтобы находился только один вариант обхода конем доски. При этом маршрут коня находится с использованием правила Варнсдорфа выбора очередного хода (предложено более 150 лет тому назад). Его суть - при обходе шахматной доски коня следует ставить на поле, из которого он может сделать минимальное количество перемещений на еще не занятые поля, если таких полей несколько, можно выбирать любое из них. В этом случае в первую очередь занимаются угловые поля и количество “возвратов” значительно уменьшается.
Вариант процедуры Solve для этого случая.
procedure Solve(x,y,l:integer);
varW:array[1..8] of integer;
xn,yn,i,j,m:integer;
begin
A[x,y]:=l;
if (l<N*N) then begin
for i:=1 to 8 do begin{формирование массива W}
W[i]:=0;xn:=x+dx[i];yn:=y+dy[i];
if (A[xn,yn]=0) the begin
for j:=1 to 8 do
if (A[xn+dx[j],yn+dy[j]]=0) the Inc(W[i]);
end else W[i]:=-1;
end;
i:=1;
while (i<=8) do begin
m:=1;{ищем клетку, из которой можно сделать наименьшее число перемещений}
for j:=2 to 8 do if W[j]<W[m] then m:=j;
if (W[m]>=0) and (W[m]<maxint)
then Solve(x+dx[m],y+dy[m],l+1);
W[m]:=maxint;{отмечаем использованную в переборе клетку}
Inc(i);
end;
end
else begin <вывод решения>;
halt;
end;
A[x,y]:=0;
end;
3. Задача о лабиринтеКлассическая задача для изучения темы. Как и предыдущие, не обходится без внимания в любой книге по информатике. Формулировка проста. Дано клеточное поле, часть клеток занята препятствиями. Необходимо попасть из некоторой заданной клетки в другую заданную клетку путем последовательного перемещения по клеткам. Изложение задачи опирается на рисунок произвольного лабиринта и две «прорисовки» с использованием простого перебора и метода «волны». Классический перебор выполняется по правилам, предложенным в 1891 г. Э.Люка в “Математических досугах”:
· в каждой клетке выбирается еще не исследованный путь;
· если из исследуемой в данный момент клетки нет путей, то возвращаемся на один шаг назад (в предыдущую клетку) и пытаемся выбрать другой путь.
Естественными модификациями задачи поиска всех путей выхода из лабиринта являются:
· поиск одного пути;
· поиск одного пути кратчайшей длины методом «волны».
Решение первой задачи.
program Labirint;
const Nmax=...;
dx:array[1..4] of integer=(1,0,-1,0);
dy:array[1..4] of integer=(0,1,0,-1);
type MyArray=array[0..Nmax+1,0..Nmax+1] of integer;
var A:MyArray;
xn,yn,xk,yk,N:integer;
procedure Init;
begin
<Ввод лабиринта, координат начальной и конечной клеток. Границы поля отмечаются как препятствия>;
end;
procedure Print;
....
begin
<вывод матрицы А - метками выделен путь выхода из лабиринта>;
end;
procedure Solve(x,y,k:integer);{k - номер шага, x,y - координаты клетки}
var i:integer;
begin
A[x,y]:=k;
if (x=xk) and (y=yk) then Print
else for i:=1 to 4 do
if A[x+dx[i],y+dy[i]]=0 then Solve(x+dx[i],y+dy[i],k+1);
A[x,y]:=0;
end;
begin
Init;
Solve(xn,yn,1);
end.
4. Задача о парламенте
На острове Новой Демократии каждый из жителей организовал партию, которую сам и возглавил. Ко всеобщему удивлению, даже в самой малочисленной партии оказалось не менее двух человек. К сожалению, финансовые трудности не позволили создать парламент, куда вошли бы, как предполагалось по Конституции острова, президенты всех партий.
Посовещавшись, островитяне решили, что будет достаточно, если в парламенте будет хотя бы один член каждой партии.
Помогите островитянам организовать такой, как можно более малочисленный парламент, в котором будут представлены члены всех партий.
Исходные данные: каждая партия и ее президент имеют один и тот же порядковый номер от 1 до N (4£N£150). Вам даны списки всех N партий острова Новой Демократии. Выведите предлагаемый Вами парламент в виде списка номеров ее членов. Например, для четырех партий:
| Президенты | Члены партий |
| 1 | 2,3,4 |
| 2 | 3 |
| 3 | 1,4,2 |
| 4 | 2 |
Список членов парламента 2 (состоит из одного члена).
Задача относится к классу NP-полных задач. Ее решение - полный перебор всех вариантов. Покажем, что ряд эвристик позволяет сократить перебор для некоторых наборов исходных данных.
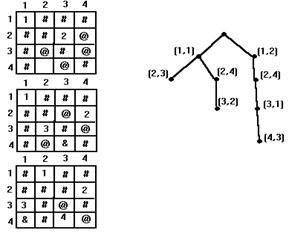
Представим информацию о партиях и их членах с помощью следующего зрительного образа - таблицы. Для примера из формулировки задачи она имеет вид:
|
|
Тогда задачу можно переформулировать следующим образом. Найти минимальное число столбцов, таких, что множество единиц из них “покрывают” множество всех строк. Очевидно, что для примера это один столбец - второй. Поговорим о структурах данных.
Const Nmax=150;
Type Nint=0..Nmax+1;
Sset=Set of 0..Nmax;
Person=record
man:Nint;{номер жителя}
number:Nint;{число партий, которые он представляет}
part:Sset;{партии}
end;
Var A:array[Nint] of Person;
Логика формирования исходных данных (фрагмент реализации).
function Num(S:Sset):Nint;{подсчитывает количество элементов в множестве}
var i,ch:Nint;
begin ch:=0;
for i:=1 to N do if i in S then Inc(ch);
Num:=ch;
end;
procedure Init;{предполагается, что данные корректны и во входном файле они организованы так, как представлены в примере из формулировки задачи}
begin
readln(N);{число жителей}
for i:=1 to N do with A[i] do begin man:=i; part:=[i]; end;{каждый житель представляет свою партию}
for i:=1 to N do begin
while Not eoln do begin read(t);A[t].part:=A[t].part+[i];{житель t представляет партию с номером i, или партия с номером i представлена жителем t}
end;
readln;
end;
for i:=1 to N do A[i].number:=Num(A[i].part);
end;
Следующим очевидным шагом является сортировка массива А по значению поля number. Становится понятным и необходимость ввода поля man в структуру записи - после сортировки номер элемента массива А не соответствует номеру жителя острова.
Пока не будем задумываться о том, как сократить перебор. Попытаемся набросать общую схему. Используемые переменные достаточно очевидны, они описываются в процессе их ввода, присвоение начальных значений глобальным переменным осуществляется в процедуре Init .
procedure Include(k:Nint);{включение в решение}
begin
Rwork:=Rwork+[A[k].man];
Inc(mn);
end;
procedure Exclude(k:Nint);{исключить из решения}
begin
Rwork:=Rwork-[A[k].man];
Dec(mn);
end;
procedure Solve(k:Nint;Res,Rt:Sset);
{k- номер элемента массива А; Res - множество партий, которые представлены в текущем решении; Rt - множество партий, которые следует “покрыть” решением; min - минимальное количество членов в парламенте; mn - число членов парламента в текущем решении; Rbest - минимальный парламент; Rwork - текущий парламент; первый вызов - Solve(1,[],[1..N])}
var i:Nint;
begin
|
блок общих отсечений |
if Rt=[] then begin if nm<min then
begin min:=mn;Rbest:=Rwork end;
end
else begin
i:=k;
while i<=N do begin
|
блок отсечений по i |
Include(i);
Solve(i+1,Res+A[i].part,Rt-A[i].part);
Exclude(i);
Inc(i);
end;
end;
end;
Очевидно, что приведенная схема решения работает только для небольших значений N, особенно если есть ограничения (а они всегда есть) на время тестирования задачи. Предварительная обработка (до первого вызова процедуры Solve), заключающаяся в проверке, есть ли жители, которые представляют все партии (это первый шаг).
procedure One(t:Nint;Q:Sset);{проверяет - есть ли среди первых t элементов массива А такой, что A[i].part совпадает с Q}
var i:Nint;
begin
i:=1;
while (i<=t) and (A[i].part<>Q) do Inc(i);
if i<=t then begin Rbest:=Rbest+[i]; Rt:=[] end;
end;
Первый вызов этой процедуры - One(N,[1..N]), осуществляется в блоке предварительной обработки.
Рассмотрим пример.
| Президенты | Члены партии |
| 1 | 2,3 |
| 2 | 4 |
| 3 | 2 |
| 4 | 1 |
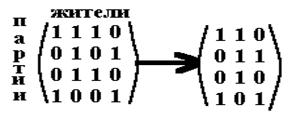
Идея. Третий житель состоит в партиях 1 и 3, второй - в 1, 2 и 3. Есть “вхождение”, третий житель менее активный, исключим его. Однако из примера проглядывает и другая идея - появилась строка, в которой только одна единица. Мы получили “карликовую” партию, ее представляет один житель, заметим, что первоначально, по условию задачи, таких партий нет. Житель, представляющий “карликовую” партию должен быть включен в решение, но он же активный и представляет еще другие партии. Значит, эти партии представлять в парламенте нет необходимости - они представлены. Исключаем эти партии (строки таблицы), но после этого возможно появление других “карликовых” партий. Рассмотрим этот процесс на следующем примере: 1 - 8,9; 2 - 10,11; 3 - 12, 13; 4 - 8,9,10; 5 - 11,12,13; 6 - 8,9,10,11; 7 - 9,10,11,12,13;8 - 1,4,6; 9 - 1,4,6,7; 10 - 2,4,6,7; 11 - 2,5,6,7; 12 - 3,5,7; 13 - 3,5,7; 14 - 8; 15 - 9; 16 - 10; 17 - 11; 18 - 12; 19 - 13.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 6 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 8 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 10 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 11 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 12 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 13 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
Выполняя операцию исключения жителей, «представительство» которых скромнее , чем у оставшихся, получаем.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
| 3 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 4 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 |
| 5 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 |
| 6 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 |
| 7 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 10 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 11 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 12 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 13 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| 14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Итак, партии с 14-й по 19-ю «карликовые», их представляют жители с 8-го по 13-й. Мы обязаны включить этих жителей в парламент. Включаем. Формируем множество партий, которые они представляют. Оказывается, что все. Решение найдено без всякого перебора.
Вывод - перебор следует выполнять не по всем жителям и не для всех партий! Если бы это выручало всегда. Сверхактивность жителей сводит на нет этот путь сокращения перебора. Остается надеяться, что кто-то должен и выращивать хлеб, а не только митинговать. Итак, “набросок” общей логики предварительной обработки.
while <есть вхождения> do begin
<исключить менее активных жителей>;
<сжать А>;
<для “карликовых” партий включить жителей, представляющих их, в состав парламента>;
<изменить значения величин, описывающих процесс формирования парламента (Res, Rt, mn, Rwork)>;
<откорректировать A>;
end;
Заметим, что необходимо исключить партии, “покрытые” жителями, представляющими карликовые партии из А[i].part оставшихся жителей. Это может привести к тому, что возможно появление жителей, представляющих все оставшиеся партии. Совместим проверку наличия вхождений, исключение части жителей и сжатие массива A в одной функции. Ее вид.
function Come(var t:Nint):boolean; {Проверяем - есть ли вхождения? Если есть, то исключаем соответствующих жителей и сжимаем массив А}
var i,j,l:Nint;
begin
for i:=1 to t-1 do
for j:=i+1 to t do if A[j].part<=A[i].part then begin
A[j].part:=[];A[j].number:=0;
end;
l:=t;
for i:=1 to t do begin
if (A[i].part=[]) and (i<=l) then begin for j:=i to l-1 do A[j]:=A[j+1];
A[l].number:=0;A[l].part:=[];
Dec(l);
end;
end;
Come:=Not(t=l);
t:=l;
end;
Вариант построения процедуры исключения «карликовых» партий может быть и таким.
procedure Pygmy(t:Nint;var r,p:Sset);{t - количество обрабатываемых элементов массива А; r - множество номеров жителей, включаемых в парламент; p - множество номеров партий, представляемых жителями, включенных в парламент}
var i,j:Nint;v:Sset;
begin
r:=[];p:=[];
for i:=1 to t do begin
{определяем множество партий представляемых всеми жителями кроме A[i].man}
v:=[];
for j:=1 to t do if i<>j then v:=v+A[j].part;
{если есть хотя бы одна партия, которую представляет только житель с номером A[i].man, то этого жителя мы обязаны включить в парламент}
if A[i].part*v<>A[i].Part then r:=r+[A[i].man];
end;
{формируем множество партий, имеющих представительство в данном составе парламента}
for i:=1 to t do if A[i].man in r then p:=p+A[i].part;
end;
Итак, фрагмент предварительной обработки (до перебора).
t:=N;Rt:=[1..N];Rwork:=[];
One(t,Rt);
while Come(t) and (Rt<>[]) do begin Rg:=[];Rp:=[];
Pygmy(t,Rg,Rp);
Rt:=Rt-Rp;Rwork:=Rwork+Rg;
if Rp<>[] then begin
for i:=1 to t do begin{исключение}
for j:=1 to N do
if (j in Rp) and (j in A[i].part) then A[i]part:=A[i].part-[j];
A[i].number:=Num(A[i].part);
end;
<сортировка А>;
end;
end;
if (Rt<>[]) then One(t,Rt);
Блок общих отсечений. Подсчитаем для каждого значения i (1£i£t) множество партий, представляемых жителями, номера которых записаны в элементах массива с i по t (массив С:array[1..N] of Sset). Тогда, если Res - текущее решение, а Rt - множество партий, требующих представления, то при Res+C[i]£Rt решение не может быть получено и эту ветку перебора следует “отсечь”.
Формирование массива С.
C[t]:=A[t].part; for i:=t-1 downto 1 do begin
C[i]:=[];C[i]:=A[i].part+C[i+1];
end;
Блок отсечений по i. Если при включении элемента с номером i в решение, значение величины Rt не изменяется, то это включение бессмысленно (A[i].part*Rt=[]).
На этом мы закончим обсуждение этой, очень интересной с методической точки зрения, задачи. Заметим, что для любой вновь возникающей идеи по сокращению перебора место для ее реализации в логике определено. А именно, предобработка, общие отсечения, покомпонентные отсечения - другого не дано.
Примечание. Графовая модель задачи (двудольный граф). Каждому жителю соответствует вершина в множестве X, каждой партии - вершина в множестве Y. Ребро (i,j) существует, если житель с номером i представляет партию с номером j. Требуется найти минимальное по мощности множество вершин S, такое, что SÍX и для любой вершины jÎY существует вершина iÎS, из которой выходит ребро в вершину j. Модификация задачи о нахождении минимального доминирующего множества.
5. Задача о рюкзаке (перебор вариантов)Постановка задачи. В рюкзак загружаются предметы n различных типов (количество предметов каждого типа не ограничено). Максимальный вес рюкзака W. Каждый предмет типа i имеет вес wi и стоимость vi (i=1,2, ..., n). Требуется определить максимальную стоимость груза, вес которого не превышает W. Обозначим количество предметов типа i через ki, тогда требуется максимизировать v1*k1+v2*k2+...+vn*kn при ограничениях w1*k1+w2*k2+...+wn*kn£W, где ki - целые (0£ki£[W/wi]), квадратные скобки означают целую часть числа.
Рассмотрим простой переборный вариант решения задачи, работоспособный только для небольших значений n (определить, для каких?). Итак, данные:
Сonst MaxN=????;
Varn,w:integer;{количество предметов, максимальный вес}
Weight,Price:array[1..MaxN] of integer;{вес, стоимость предметов}
Best,Now:array[1..MaxN] of integer;{наилучшее, текущее решения}
MaxPrice:LongInt;{наибольшая стоимость}
Решение, его основная часть - процедура перебора:
Procedure Rec(k,w:integer;st:LongInt);
{k - порядковый номер группы предметов, w - вес, который следует набрать из оставшихся предметов, st - стоимость текущего решения}
var i:integer;
begin
if (k>n) and (st>MaxPrice) then begin {найдено решение}
Best:=Now;MaxPrice:=st; end
else if k<=n then
for i:=0 to w div Weight[k] do begin
Now[k]:=i;
Rec(k+1,W-i*Weight[k],st+i*Price[k]);
end;
end;
Инициализация переменных, вывод решения и вызывающая часть (Rec(1,w,0)) очевидны. В данной логике отсутствуют блоки предварительной обработки, общих отсечений и отсечений по номеру предмета (смотрите задачу о парламенте). В блоке предварительной обработки целесообразно найти какое-то решение, лучше, если оно будет как можно ближе к оптимальному (наилучший вариант загрузки рюкзака). «Жадная» логика дает первое приближение. Кроме того, разумно выполнить сортировку, например, по значению стоимости предметов или отношению веса предмета к его стоимости. Построение блока общих отсечений аналогично тому, как это сделано в задаче о парламенте, а ответ на вопрос, почему предметы данного типа не стоит складывать в рюкзак, остается открытым.
Заключение
Инициализация переменных, вывод решения и вызывающая часть (Rec(1,w,0)) очевидны. В данной логике отсутствуют блоки предварительной обработки, общих отсечений и отсечений по номеру предмета (смотрите задачу о парламенте). В блоке предварительной обработки целесообразно найти какое-то решение, лучше, если оно будет как можно ближе к оптимальному (наилучший вариант загрузки рюкзака). «Жадная» логика дает первое приближение. Кроме того, разумно выполнить сортировку, например, по значению стоимости предметов или отношению веса предмета к его стоимости. Построение блока общих отсечений аналогично тому, как это сделано в задаче о парламенте, а ответ на вопрос, почему предметы данного типа не стоит складывать в рюкзак, остается открытым.
Литература
1. Ахо А.,Хопкрофт Д., Ульман Д. Построение и анализ вычислительных алгоритмов.-М.:Мир,1979.
2. Гэри М., Джонсон Д. Вычислительные алгоритмы и труднорешаемые задачи.-М.:Мир, 1982.
3. Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы: Теория и практика.-М.:Мир,1980.
4. Суханов А.А. Олимпиадные задачи. Неопубликованный материал. - СПб.: 1996.