Дипломная работа: Мультипликативные полугруппы неотрицательных действительных чисел

Содержание

Введение 3

Основные понятия и определения 4

Глава 1. Делимость в мультипликативных полугруппах_ 7

§1. Свойства НОД и НОК_ 7

§ 2. Строение числовых НОД и НОК полугрупп_ 11

Глава 2. Мультипликативные полугруппы неотрицательных чисел со свойствами (*) и (**) 15

Библиографический список 19


           Введение

В математических исследованиях  множество действительных чисел R очень популярно как бескрайний источник простых примеров и как множество, использующееся во многих структурах.

Рассматриваемое в данной работе множество неотрицательных действительных чисел – это интересное легко интерпретируемое подмножество R.

Как известно, различные подалгебры множества R+ (например, полугруппа N) исследовались ранее. В этой работе мы продолжим изучение мультипликативных полугрупп неотрицательных действительных чисел с 0 и 1.

Работа состоит из двух глав. Первая глава содержит некоторые свойства наибольшего общего делителя и наименьшего общего кратного элементов целой полугруппы (§1). В этой же главе говорится о строении НОД и НОК полугрупп. Во второй главе получена топологическая классификация мультипликативных полугрупп SR+, обладающих одним из введенных специфических свойств:

(*)      (a<b);

(**)    (0<a<b).


 Основные понятия и определения

 

Определение 1. Пусть Х – множество произвольной природы и t – семейство подмножеств Х, называемых открытыми, удовлетворяющее условиям:

1)   пересечение конечного числа множеств из t принадлежит t,

2)   объединение любого множества множеств из t принадлежит t,

3)    и ÆÎt.

Тогда  называется топологическим пространством, t – топологией на Х.

Определение 2. Дополнения открытых множеств в Х называются замкнутыми множествами.

Определение 3. Пусть  – топологическое пространство и . Введем на множестве Х1 топологию t1. Открытыми в пространстве  назовем все множества вида , где U – произвольное открытое множество в Х. Тогда пространство  называется подпространством топологического пространства , а топология t1 – топологией, индуцированной топологией t на множество Х1.

Определение 4. Семейство открытых множеств в топологическом пространстве  называется базой топологии t, если любое открытое множество в Х является объединением множеств из этого семейства.

Пример. На числовой прямой R с естественной (евклидовой) топологией открытыми множествами являются всевозможные объединения интервалов, они и образуют базу этой топологии. На множестве неотрицательных чисел R+ эта топология индуцирует топологию, в которой открытым множеством будет, например,  R+Ç (-1, 1).

Определение 5. Пространство Х1 называется плотным подпространством пространства Х, если любое непустое открытое множество в Х содержит точки множества Х1.

Очевидно, Х1 плотно в Х, если каждая точка подпространства Х1 является предельной точкой множества Х.

Определение 6. Множества в топологическом пространстве, являющиеся одновременно открытыми и замкнутыми, называются открыто-замкнутыми.

Определение 7. Топологическое пространство Х называется связным если открыто-замкнутыми множествами в нем являются лишь Х и Æ.

Определение 8. Множество Х1  в топологическом пространстве Х называется связным, если оно связно как топологическое подпространство пространства Х.

Примеры:

1. Множество точек плоскости является связным, если в нем любую пару точек можно соединить кривой.

2. На числовой прямой связными множествами являются лишь промежутки.

Определение 9. Топологическое пространство называется нульмерным, если оно обладает базой из открыто-замкнутых множеств.

Пример. Дискретное топологическое пространство, в котором все его подмножества являются открытыми, – нульмерно.

Далее везде будем обозначать символом S мультипликативную полугруппу.

Определение 10. Множество S с бинарной операцией умножения × называется мультипликативной полугруппой, если эта операция обладает свойством ассоциативности, т.е. .

Определение 11. Элемент bS называется делителем элемента аS, если  для некоторого . При этом говорят, что  делится на , или  делит  (|).

Определение 12. Общий делитель элементов  и , делящийся на любой их общий делитель, называется наибольшим общим делителем элементов  и  и обозначается НОД.

Определение 13. Элемент S называется кратным элементу S, если a делится на b.

Определение 14. Общее кратное элементов  и , на которое делится любое их общее кратное, называется наименьшим общим кратным элементов  и  и обозначается НОК.

Определение 15. Полугруппа S называется НОД-полугруппой (НОК-полугруппой), если любые два элемента из S имеют наибольший общий делитель (наименьшие общее кратное).

Определение 16. Элемент  из S называется неприводимым, если он имеет ровно два делителя 1 и а. Неприводимые элементы не представимы в виде произведения неединичных элементов, т.е. если .

Определение 17. Элемент  из S называется простым, если . Очевидно, простые элементы неприводимы.

Определение 18. Полугруппа S называется топологической полугруппой, если на множестве S введена топология, и топологическая и алгебраическая структуры в S согласованы, т.е.

1)         áS, ×ñ– полугруппа;

2)         S – топологическое пространство;

3)         полугрупповая операция × непрерывна в S:

.


 Глава 1. Делимость в мультипликативных полугруппах

 

§1. Свойства НОД и НОК

Пусть S – коммутативная мультипликативная несократимая полугруппа с 1 и без делителей единицы. Такие полугруппы называются целыми, или коническими.

Элементы  и  из S называются взаимно простыми, если НОД(,)=1.

Предварительно рассмотрим простейшие свойства отношения делимости в целых полугруппах.

Свойства делимости в целых полугруппах

(1) ;

(2)  – рефлексивность;

(3)  – антисимметричность;

(4)  – транзитивность;

(5) ;

(6) ;

(7) Любой простой элемент неприводим;

(8) р неприводим Û ;

Свойство 1. НОД и НОК нескольких элементов определены однозначно, если существуют.

Доказательство. Проведем доказательство для НОД двух элементов а и b из S. Пусть (a,b) и (a,b). Тогда из определения НОД следует  и . По свойству антисимметричности имеем .

Свойство 2. .

Доказательство. Импликации  и  очевидны. Пусть , т.е.  для некоторого . Очевидно, b – общий делитель а и b. Возьмем произвольный общий делитель с элементов а и b. Для него существуют такой  элемент , что  и . Таким образом, с делит b. Это и означает, что . Аналогично доказывается .

Следствие 1. .

Следствие 2.  и .

Свойство 3.  и .

Доказательство следует из коммутативности операции умножения и свойств делимости.

Свойство 4. .

Доказательство. Обозначим d1=НОД(НОД(a,b),c). Так как d1 является общим делителем НОД(a,b) и c, то d1 – общий делитель и для элементов a,b и c. Верно и обратно: любой общий делитель этих трех элементов является общим делителем для НОД(a,b) и c. Аналогичным свойством обладает и элемент d2=НОД(a, (НОД(b,c)).  Тогда элементы d1 и d2 делят друг друга. По свойству антисимметричности делимости получаем d1=d2.

Свойство 5. .

Доказательство. Обозначим k1=НОК(НОК(a,b),c). Так как k1 является общим кратным элементов НОК(a,b) и c, то k1 – общее кратное и для элементов a,b и c. Верно и обратно: любое общее кратное этих трех элементов является общим кратным для НОК(a,b) и c. Аналогичным свойством обладает и элемент k2=НОК(НОК(a,b),c).  Тогда элементы k1 и k2 делят друг друга. По свойству антисимметричности делимости получаем k1=k2.

Свойство 6. Если элементы а и b не взаимно просты, то а и b имеют общий делитель, не равный 1.

Доказательство. По условию НОД(a,b)=d¹1. Тогда по определению d и есть не равный единице общий делитель а и b.

Свойство 7. =.

Доказательство. Обозначим d=НОД(a,b). По свойству (6) делимости элемент сd делит любой общий делитель элементов ас и bс, следовательно, является их НОД. Свойство доказано.

Свойство 8. Если , то .

Доказательство. Из условия  следует, что d делит любой общий делитель элементов а и b и . Тогда по свойству (6) делимости элемент  делит любой общий делитель элементов , следовательно, является их НОД. Свойство доказано.

Свойство 9. Если  и , то .

Доказательство. Пусть НОД и НОД(а,b) = 1, тогда среди делителей элементов b и с нет делителей элемента а. Следовательно, и среди делителей элемента bc нет делителей элемента а, что и означает, что .

Свойство 10. Если , то  для любых N.

Доказательство. Докажем, что  методом математической индукции. Пусть m = 1, тогда  по условию, т.е. база индукции верна. Предположим, что  для всех k < m. Покажем, что  при k = m.  по свойству (10) для с = b. Отсюда,  для всех N.  по свойству 3 делимости. Аналогичными рассуждениями получаем  для любого N. Следовательно, .

Свойство 11. Если , то  для любого .

Доказательство. Пусть , тогда а = sd и c = td для некоторых s,tS таких, что НОД(s,t) = 1. Поскольку , то НОД(s,b) = 1 и по свойству 9 НОД(s,tb) = 1. Следовательно, . Свойство доказано.

Свойство 12. Существование НОК(a,b) влечет существование НОД(a,b) и равенство НОД(a,b) НОК(a,b) = ab.

Доказательство. Если хотя бы одно из чисел  или  равно 0, то  и равенство справедливо. Пусть элементы  и  ненулевые и . Поскольку  - общее кратное чисел  и , то  для некоторого . Так как  и , то  - общий делитель  и . Докажем, что  делится на любой общий делитель элементов  и . Пусть  - произвольный общий делитель чисел  и , т.е.  и  для некоторых . Поскольку  - общее кратное элементов  и , то . Так как , то  для некоторого . Отсюда . Следовательно, , и, значит, НОД().

Предложение 1. Полугруппа  является НОК-полугруппой тогда и только тогда, когда  есть НОД-полугруппа.

Доказательство. По свойству 12 достаточно доказать, что любая НОД-полугруппа является НОК-полугруппой. Пусть  есть НОД-полугруппа. Возьмем произвольные . Если хотя бы одно из чисел  равно 0, то . Рассмотрим случай  и . Обозначим . Тогда  и  для некоторых . Поскольку   по свойству 7, то . Положим . Число  является общим кратным элементов  и . Осталось показать, что на  делится любое общее кратное  и . Возьмем произвольное общее кратное  элементов  и , т. е.  для некоторых . Тогда , т.е.  (поскольку ). По свойству 11 имеем , значит,  для некоторого . Поэтому , т.е. .

§ 2. Строение числовых НОД и НОК полугрупп

Далее будем рассматривать множество всех неотрицательных действительных чисел R+ и мультипликативную полугруппу SR+, содержащую 0 и 1, с топологией, индуцированной топологией числовой прямой.

Лемма 1. Если S связно, то S= или S=R+.

Доказательство. Пусть S связное множество в R+. Тогда S является промежутком. Поскольку  и , то . Если в S нет элемента c > 1, то . В противном случае числа  (N) принимают сколь угодно большие значения. Поскольку S – промежуток, то  для всех N. Отсюда R+.

Лемма 2. Если  несвязно, то .

Доказательство. Предположим, что . Тогда в силу несвязности  существуют такие числа , что  и . Так как , то . Тогда . Полученное противоречие завершает доказательство.

Лемма 3. Если , то  или =R+.

Доказательство. Очевидно,  - полугруппа. Пусть  и . Тогда существует элемент . Докажем, что . Возьмем произвольное . Пусть натуральное N таково, что . Тогда из  следует . Отсюда . Лемма доказана.

Лемма 4. Пусть S – НОД-полугруппа и пространство S несвязно. Тогда:

1)         (0,с)S для любого ,

2)         если , то и для любого .

Доказательство. 1) Если в интервале (0,1) нет элементов из S, то заключение очевидно. Пусть (0,1)ÇS¹Æ. Предположим, что (0,c)S для некоторого . Не теряя общности, будем считать, что . Так как S несвязно, то по лемме 2 существует s[0, 1]\S. Возьмем в S ненулевой элемент  и положим b=asS. Пусть d=НОД(a,b). Поскольку 0<s<1, то sn0 при n. Тогда sN < c для некоторого натурального N, и, значит, sNS. По свойству 8, пункт (3), НОД(a/d, b/d)=1. Поскольку b/d:a/d=sS, то элемент a/d необратим в S. Очевидно, необратимым является и (a/d)N. По свойству 11, пункт (5), имеем НОД((a/d)N, (b/d)N)=1. Из (b/d)N:((a/d)N=sNS следует, что НОД((a/d)N, (b/d)N)=(a/d)N. Значит, элемент (a/d)N ассоциирован с 1, т. е. обратим. Получили противоречие. Следовательно, (0, с)S для любого .

2) Если , то заключение справедливо. Пусть  и . Тогда по лемме 3 существует s. Предположим, что  для некоторого с >1. Возьмем в S элемент  и положим b=asS. Поскольку s>1, то sn+¥ при n. Следовательно, sN>c для некоторого натурального N, и, значит, sNS. Повторяя рассуждения, проведенные выше, заключаем:  для любого .

Предложение 2. Пусть S – НОД-полугруппа. Если пространство S несвязно и , то S нульмерно.

Доказательство. Докажем, что при выполненных условиях в любом интервале , где , есть точки, не принадлежащие S. Доказывая от противного, предположим, что [a,b]S для некоторых . Возможны два случая.

Случай 1. Пусть 0<a<. Докажем, что найдется n0N, для которого ab. В самом деле, допуская, что b<a для всех nN и, переходя в неравенстве b<a к пределу при n, получили бы ba<b. Откуда b>a для всех натуральных n>n0. Тогда 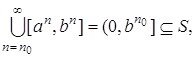 что невозможно по лемме 4.

Случай 2. Пусть . Возьмем такое число с > a, чтобы 1<c<b. Рассуждая, как и в случае 1, получаем cb для некоторого n0N. Тогда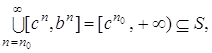 что также невозможно по лемме 4.

Докажем, что S нульмерно. Пусть V – произвольное открытое множество в S и . Требуется показать, что существует такое открыто-замкнутое в S множество U, что . Поскольку топология в S индуцируется топологией числовой прямой, то существуют такие числа a и b , что . Если , то это и есть открыто-замкнутое множество U. Пусть левее s в интервале  нет точек множества S, а правее – есть, и точка с - одна из них. По доказанному выше существует точка , такая, что . В этом случае  – искомое открыто-замкнутое множество U. Аналогично рассматривается случай, когда левее точки s в интервале  есть точки множества S, а правее нет, и случай, когда интервал  содержит точки из S и справа и слева от s. Предложение доказано.

С помощью предложения 2 можно получить следующую топологическую классификацию числовых НОД-полугрупп.

Предложение 3. Любая НОД-полугруппа S относится к одному из следующих классов:

1.         S связно.

2.         S нульмерно, замкнуто в R+ и 0 – предельная точка для S.

3.         S нульмерно, не замкнуто в R+ и 0 – предельная точка для S.

4.         Точка 0 изолирована в S.

Доказательство. По лемме 1 существуют полугруппы , которые являются связными множествами. Пусть  несвязно. Если =Æ, то 0 – изолированная точка. Если существует элемент , то  для любого N и последовательность  сходится к 0. Следовательно, 0 – предельная точка для S, множество  при этом может быть как замкнутым в R+, так и не замкнутым. Предложение доказано.


 Глава 2. Мультипликативные полугруппы неотрицательных чисел

со свойствами (*) и (**)

В этой главе на основе предложения 2 дадим топологическую классификацию полугрупп S, которые обладают одним из следующих свойств:

(*)      (a<b);

(**)    (0<a<b).

Лемма 8. Полугруппа S, удовлетворяющая хотя бы одному из свойств (*), (**) является НОД-полугруппой и НОК-полугруппой. При этом, в первом случае НОД(a,b)= max{a,b}, НОК(a,b)= min{a,b} для любых a,bS, а во втором случае – НОД(a,b)= min{a,b}, НОК(a,b)= max{a,b}, если числа  и  не равны нулю.

Доказательство. Пусть полугруппа S обладает свойством (*). Покажем, что любые два элемента  имеют НОД и НОК. По свойству (*) a =  и S. Получили, что элемент b является делителем a. Следовательно, по свойству 2 делимости НОД(a,b) = b = max{a,b} и НОК(a,b) = а = min{a,b}. Аналогичными рассуждениями можно показать, что если полугруппа S обладает свойством (**), то для любых ненулевых элементов  и  НОД(a,b)= min{a,b}, НОК(a,b)= max{a,b}. Пусть хотя бы одно из чисел а или b равно 0, например, b. Тогда НОД(a,b) = НОД(а,0) = а и НОК(a,b) = НОК(а,0) = а.

Лемма 9. Если в полугруппе S со свойством (*) существует элемент c > 1, то S \ {0} – группа.

Доказательство. Докажем, что в S произвольный ненулевой элемент a < 1 обратим. Элемент acn > 1 для некоторого nN. Тогда 1 / acn S в силу свойства (*). Откуда 1 / a = (1 / acn) cn S.

Предложение 4. Любая полугруппа S со свойством (*) относится к одному из следующих классов:

1.         S = [0,1].

2.         S = R+.

3.         S = {rn | n = 0,1,2,…}, где 0 < .

4.         S = {rn | nZ}, где 0 < .

5.         S – нульмерное плотное подпространство в [0,1].

6.         S – нульмерное плотное подпространство в R+.

7.         S = {0,1}.

Доказательство. Если  связно, S= или S=R+ по лемме 1.

Пусть S несвязно. Поскольку полугруппа {0}È[1,+) не обладает свойством (*), то S нульмерно. Предположим сначала, что S замкнуто (в R+). Если в S ровно два элемента, то S = {0,1}. Пусть поэтому . Покажем, что точка 1 изолирована в S. Предположим, что это не так. Тогда в S существует строго возрастающая последовательность (еn), сходящаяся к 1. Так как S замкнуто и несвязно, то в (0,1) найдутся такие элементы c < d, что (c,d) =  по лемме 4. В то же время строго возрастающая последовательность (en,d) элементов из S сходится к числу d. Противоречие. Следовательно, 1 является изолированной точкой в S. Обозначим . Тогда  . Возьмем произвольный ненулевой элемент  из . Для него  при некотором N. По свойству (*) получаем  и . Поскольку , то . Тогда в случае S имеем 0,1,2,…, а в противном случае Z по лемме 9.

Пусть S нульмерно и не замкнуто. Существует монотонная последовательность чисел 0аnS, сходящаяся к некоторому аS. Пусть bn = an / an+1, если (an) возрастает, и bn = an+1 / an, если она убывает. Тогда bnS (N) и bn1 при . Возьмем произвольное число с(0,1). Для каждого N найдется такое k(n)N, что . Тогда имеем  и .

Следовательно, числа N из  образуют плотное подмножество в [0,1]. Если S, то получаем случай 5. Если же S, то по лемме 9 получаем случай 6. Предложение доказано.

Предложение 5. Любая полугруппа S со свойством (**) относится к одному из следующих классов:

1.         S = R+.

2.         S = {rn | nÎN}, где .

3.         S = {rn | nZ}, где .

4.         S\{0} – нульмерное плотное подпространство в [1,).

5.         S – нульмерное плотное подпространство в R+.

6.         S = {0,1}.

7.         È[1,+¥).

Доказательство. Пусть  связно. Поскольку полугруппа [0,1] не обладает свойством (**), то по лемме 1 получаем S=R+.

Очевидно,  является полугруппой со свойством (**).

Пусть далее  несвязно и . Тогда  нульмерно по предложению 2.

Пусть  замкнуто и Æ. Если в  нет элемента, большего 1, то . Пусть (1,+¥)¹Æ. Докажем, что точка 1 изолирована в . Допустим, что это не так. Тогда в  существует строго убывающая  последовательность, сходящаяся к 1. Так как  замкнуто и несвязно, то в [1,+¥) есть такие элементы , что . В то же время строго убывающая последовательность  элементов из  сходится к числу , следовательно, ее члены, начиная с некоторого номера, попадают в интервал . Получили противоречие. Следовательно, 1 является изолированной точкой в . Обозначим . Тогда  и поскольку  замкнуто, то . Возьмем произвольный элемент  из . Для него  при некотором N. По свойству (**) получаем  и . Поскольку , то . В этом случае N.

Пусть  замкнуто и Æ. Как и выше, доказывается, что 1 – изолированная точка. Обозначим  и . Тогда , . Так как  замкнуто, то . Из свойства (**) следует, что . Из неравенства  по доказанному выше получаем:  для некоторого натурального N. Поскольку , то . В этом случае Z.

Пусть  не замкнуто и Æ. Тогда существует монотонная последовательность чисел , сходящаяся к некоторому . Пусть , если последовательность элементов  убывает, и , если она возрастает. Тогда  для всех N и  при . Возьмем произвольное число . Для каждого N найдется такое N, что . Тогда имеем  и .

Следовательно, числа N из  образуют плотное подмножество в [1,+ ¥) (случай 4).

Если  не замкнуто и Æ, то аналогичные рассуждения показывают, что S – плотное подпространство в R+.

Следствие 1. Любая полугруппа S, обладающая свойствами (*) и (**) относится к одному из следующих классов:

1.         S = R+.

2.         S – нульмерное плотное подпространство в R+.

3.         S = {0,1}.


   Библиографический список

1.         Варанкина, В.И., Полукольца непрерывных неотрицательных функций: делимость, идеалы и конгруэнции [Текст] // В. И. Варанкина, Е. М. Вечтомов, И. А. Семенова / Фундаментальная и прикладная математика. 1998. Т. 4. № 2. С  493-510.

2.         Курош, А.Г. Лекции по общей алгебре [Текст] / А. Г. Курош. – М.: Наука, 1973.