Дипломная работа: Положительные и ограниченные полукольца

Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования
Вятский государственный гуманитарный университет

Математический факультет

Кафедра алгебры и геометрии

Выпускная квалификационная работа

Положительные и ограниченные полукольца

Выполнил:

студент V курса математического факультета

Ворожцов Вячеслав Андреевич   _____

Научный руководитель: 

кандидат физико-математических наук, доцент кафедры алгебры и геометрии В.В. Чермных   ________

Рецензент:

доктор физико-математических наук, профессор кафедры алгебры и геометрии Е.М. Вечтомов   _______

Допущена к защите в государственной аттестационной комиссии

«___» __________2005 г.     Зав. кафедрой                             Е.М. Вечтомов

«___»___________2005 г.     Декан факультета                     В.И. Варанкина

Киров

2005

Содержание

Введение........................................................................................................... 3

Глава 1. Основные понятия теории полуколец ............................................. 4

1.1. Определение полукольца. Примеры.................................................. 4

1.2. Дистрибутивные решетки.................................................................... 5

1.3. Идеалы полуколец............................................................................... 6

Глава 2 Положительные и ограниченные полукольца.................................. 7

2.1. Определение и примеры положительных и ограниченных полуколец      7

2.2. Основные свойства положительных и ограниченных полуколец..... 7

Библиографический список........................................................................... 16

Введение

Теория полуколец – это раздел современной алгебры, обобщающий как кольца, так и дистрибутивные решетки. Понятие полукольца возникло в 30-х годах прошлого столетия. Как самостоятельная теория полукольца начали изучаться в 50-е годы. Особенно интенсивно теория полуколец развивается последние 20 лет, что вызвано не только теоретическим интересом, но и многочисленными ее приложениями.

Целью данной работы является изучение классов положительных и ограниченных полуколец, рассмотрение основных свойств данных алгебраических объектов, часть из которых доказывается автором работы самостоятельно; приведены примеры полуколец.

Работа состоит из 2 глав. В первую главу вошли основные определения и факты, на которые опирается эта работа. Вторая – основная часть всей работы, в ней рассмотрены определения и свойства положительных и ограниченных полуколец, приведены примеры, доказаны некоторые теоремы.

Глава I. «Основные понятия теории полуколец».

1.1. Определение полукольца. Примеры.

Определение полукольца: Непустое множество S с бинарными операциями + и · называется полукольцом, если выполняются следующие аксиомы:

1.  (S,+) – коммутативная полугруппа с нейтральным элементом 0;

·     Ассоциативность: ;

·     Коммутативность: ;

·     Существование нейтрального элемента: .

2.  (S,·) – полугруппа:

·     Ассоциативность: ;

3.  Умножение дистрибутивно относительно сложения:

·     левая дистрибутивность:  а(в+с)=ав+ас;

·     правая  дистрибутивность:  (а+в)с=ас+вс.

4.  Мультипликативное свойство 0:

·     .

Эта аксиоматика появилась в 1934 году и ее автором является Вандовер.

Полукольцо S называется коммутативным, если операция  в нем коммутативна: .

Полукольцо S называется полукольцом с единицей, если в нем существует нейтральный элемент по умножению, который называется единицей (1):

Примеры полуколец:

1.   <N,+,·>, где N – множество неотрицательных целых чисел с обычными операциями + и ·;

2.   <{0},+,·> - тривиальное полукольцо;

3.   Двухэлементные полукольца:<Z₂ ,+,·>, <В,+,·> (в В 1+1=1);

4.   Множество матриц с элементами из полукольца N и операциями + и ;

5.   Множества N, Z, Q⁺, Q, R⁺, R и введенных на них различных комбинаций операций: обычные сложение и умножение, максимум  и минимум  двух чисел, НОД и НОК, когда они определены.

Полукольцо с импликацией   называется мультипликативно (аддитивно) сократимым.

Полукольцо, в котором выполняется равенство  , называется мультипликативно (аддитивно) идемпотентным.

1.2. Дистрибутивные решетки.

Пусть L – произвольное множество. Введем на L отношение  положив,

.

Отношением порядка называется рефлексивное, транзитивное, антисимметричное бинарное отношение на множестве L, при этом множество L назовем частично упорядоченным множеством.

Отношение  на множестве L является отношением порядка.   

Пусть M – непустое подмножество частично упорядоченного множества L . Нижней гранью множества M называется такой элемент , что   для любого . Нижняя грань m множества M называется точной нижней гранью, если , где n – произвольная нижняя грань множества M. Двойственным образом определяется точная верхняя грань.

Частично упорядоченное множество L называется решеткой, если любые два элемента имеют точную верхнюю  и точную нижнюю  грани; решетка называется дистрибутивной, если в ней выполняются дистрибутивные законы:

Кроме этого определения существует еще одно определение дистрибутивной решетки. Алгебраическая система L с двумя бинарными операциями сложения + и умножения ∙ называется решеткой, если (L, +) и (L,∙) являются идемпотентными коммутативными полугруппами и операции связаны законами поглощения

 ,;

Решетка называется дистрибутивной, если для любых  , ограниченной, если она имеет 0 и 1.

1.3. Идеалы полуколец.

Непустое подмножество I полукольца S называется левым (правым) идеалом полукольца S, если для любых элементов a, bI, sS элементы a+b и sa (as) принадлежат I.

Непустое подмножество, являющееся одновременно левым и правым идеалом, называется двусторонним идеалом или просто идеалом полукольца. Идеал, отличный от полукольца S называется собственным. Наименьший из всех (левых) идеалов, содержащий элемент a S, называется главным (главным левым) идеалом, порожденным элементом a. Обозначается (a) или SaS, односторонние Sa и aS – левый и правый соответственно. Множество всех элементов принадлежащих главному идеалу можно записать так .

Собственный идеал M полукольца S называется максимальным (максимальным правым) идеалом, если  влечет M=A или A=S для каждого идеала A .

Примерами идеалов могут служить следующие подмножества:

1.    {0} – нулевой идеал;

2.    S – идеал, совпадающий со всем полукольцом;

3.    Идеал на полукольце : ;

4.    Главный идеал ограниченной дистрибутивной решетки L, порожденный элементом a: .

Глава II «Положительные и ограниченные  полукольца».

2.1. Определение, примеры  и основные свойства.

Полукольцо S  с 1 называется положительным, если для любого элемента а  S элемент а+1 обратим в S, т.е..

Примерами положительных полуколец служат следующие алгебраические системы:

1.        ограниченные дистрибутивные решетки;

2.        полукольца непрерывных R⁺ - значных функций;

3.        множество всех идеалов полукольца, с операциями сложения и умножения.

Полукольцо S называется ограниченым, если для любого  выполняется . Ограниченное полукольцо – частный случай положительного полукольца.

Примеры ограниченных полуколец:

1.        ограниченные дистрибутивные решетки;

2.        множество всех идеалов полукольца, с операциями сложения и умножения.

2.1.Основные свойства положительных и ограниченных  полуколец:

I.                  Для полукольца S следующие условия равносильны:

1. S – положительное полукольцо;

2. для любого максимального одностороннего идеала M в S и любых a и b  S

(a+b  M) (a  M & b  M).

Доказательство:

12. Пусть для произвольных  и максимального правого идеала M. Предположим, что , тогда  и для некоторых  и . Имеем:

.

В левой части последнего равенства – элемент из M, тогда как в правой части обратимый справа элемент; противоречие.

21. Пусть выполнено 2 и с – произвольный элемент из S. Элемент 1+с не лежит ни в одном максимальном одностороннем идеале полукольца S (т.к.  в противном случае в силу условия 2 в идеале должен лежать элемент 1, противоречие), значит, 1+с обратим.

II. В положительном полукольце S справедливы импликации:

Доказательство. Пусть . Поскольку S положительно, то для x+1 найдется некоторый , такой что . Тогда

,т.к.. Получили y=1 и значит .

Таким образом мы доказали, если положительное полукольцо мультипликативно идемпотентно, то оно ограниченно,

Теперь, пусть , тогда ,т.е. такое полукольцо еще и аддитивно идемпотентно.

Поскольку  выполняется для , то для x=1, также выполняется. Обратно, 1+1=1, помножим обе части на x и получим необходимое равенство.

III . Полукольцо S положительно тогда и только тогда, когда для любого элемента  и любого обратимого элемента  элемент  обратим.

Доказательство.

 Полукольцо положительно, следовательно, элемент  - обратим. Умножим обратимый элемент на обратимый, получим обратимый.

В левой части обратимый элемент, значит и в правой элемент тоже обратим.

   и  – обратимы,  тогда их произведение также обратимо , значит обратим.

IV . Для коммутативного положительного полукольца S равносильны следующие условия:

1.   S – дистрибутивная решетка.

2.  

Доказательство.

. Очевидно.

. По свойству  2 следует , тогда:

 и .

Эти условия наряду с ассоциативностью, коммутативностью и идемпотентными законами определяют дистрибутивную решетку.

V. В ограниченном полукольце единица 1 – единственный обратимый элемент.

Доказательство.

Пусть есть некоторый обратимый элемент u,

 и

VI. Пусть a – фиксированный элемент полукольца S, тогда каждое из утверждений влечет следующее утверждение:

1.   a+1=1;

2.     

3.    

Доказательство.

. Докажем методом математической  индукции по числу n.

I.              База. к=1. (выполняется по условию).

II. Индуктивное предположение. Пусть для к<n условие выполняется, т.е.

Рассмотрим для k=n

 и a+1=1

Из I и II Следует .

. .

Можно выбрать из всего количества N, некоторое число, для которого тоже данное выражение будет верно.

Примером того , что условие 3 не влечет условие 1 является полукольцо матриц . Зафиксируем элемент , где . Для n=2

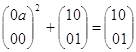 верно, но  совсем неверно.

VII. Если  S – полукольцо с мультипликативным сокращением и аддитивно идемпотентно, то все утверждения предыдущего свойства равносильны.

Доказательство.

Осталось доказать .

Имеем  . Добавим к правой и левой части выражения равные элементы :

В силу аддитивной идемпотентности мы можем подбирать коэффициенты перед . В соответствии с биномом Ньютона, подберем коэффициенты и получим:

Используя мультипликативную сократимость, получим a+1=1. Что и доказывает равносильность условий 1 – 3.

VIII. Пусть S – ограниченное полукольцо, и существует такое  , что  для всех . Тогда:

1.          для всех ;

2.          - коммутативное ограниченное полукольцо с 1, где I – множество всех мультипликативных идемпотентов из S, а операцияопределяется так:

.

Доказательство.

1.         Возьмем .

Тогда , т.к. .

Для доказательства понадобится

Лемма: В ограниченном полукольце

.

Доказательство: ММИ по числу n в  .

I. База. n=1.  Из условия ограниченности

II. И.П. n=i-1.

 Из условия II и ограниченности:

.

По ИП:

Из условий I,II получили, что данное равенство верно для , лемма доказана.

Рассмотрим :

Поскольку степень равна 2n-1, то в каждом из составляющих сумму слагаемых, либо (1 группа), либо  (2 группа), и только так.

Среди слагаемых 1 группы имеется член . Этот член в сумме с каждым слагаемым 1 группы будет давать самого себя, при условии  и лемме 1. из группы 1 останется только элемент

Аналогично с элементами группы 2, в которой имеется элемент , который и останется. Получаем

2 .Прежде всего проверим замкнутость операций  и + на множестве I.

(1) Поскольку в качестве аддитивной операции выбрано сложение, и все элементы из полукольца, значит (I,+) – коммутативная полугруппа с нейтральным элементом 0.

(2) Докажем, что  - коммутативная полугруппа с нейтральным элементом 1:

a). Ассоциативность:

Рассмотрим элемент

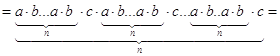
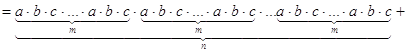
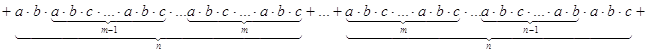
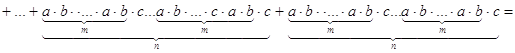
Элемент X состоит из таких слагаемых, которые получены при умножении, кроме тех которые получены при произведении со всеми 1, или со всеми с. Элемент  имеется в качестве сомножителя в каждом слагаемом X, т.е.

С другой стороны

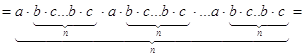
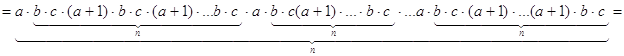
Таким образом, правые части рассматриваемых тождеств равны, значит ассоциативность доказана.

b). 1 – нейтральный элемент:

с). Коммутативность:

,

1.

2.

Из 1 и 2 следует , по причине равенств правых частей каждого, а значит следует равенство . Коммутативность доказана.  - коммутативная полугруппа с нейтральным элементом 1.

(3) Дистрибутивность:

(4)      

Все аксиомы полукольца доказаны, а значит  - коммутативное полукольцо и его элементы – элементы ограниченного полукольца, значит полукольцо – ограничено.

IX. Если в положительном полукольце S выполняется равенство

 ,

то S – аддитивно идемпотентно.

Доказательство.

Рассмотрим  t>1

Рассмотрим  t=1,

…

т.к. полукольцо положительно, то в обеих частях обратимые элементы, домножим на обратный и получим 1+1=1, умножим обе части на u, получим u+u=u, что и означает аддитивную идемпотентность.

X.        В положительном полукольце S   справедливо следующее тождество:

Доказательство.

Домножим на обратный  к :  

Получим:

Что и требовалось доказать.

Библиографический список

1.            Чермных, В.В. Полукольца [Текст] / В.В. Чермных – Киров: Изд-во ВГПУ, 1997. – ст.7 – 87.

2.            Вечтомов, Е.М. Введение в полукольца [Текст] / Е.М. Вечтомов – Киров: Издательство ВГ ПУ, 2000. – ст.5 - 30.