Курсовая работа: Полунормальные подгруппы конечной группы
Дипломная работа
"Полунормальные подгруппы конечной группы"
Содержание
Введение
1 Силовские подгруппы конечных групп
2 Полунормальные подгруппы
2.1 Свойства супердобавлений
2.2 Супердобавления к максимальным подгруппам
2.3 Супердобавления к силовским подгруппам
3 Факторизации групп дисперсивными и сверхразрешимыми подгруппами
3.1 Силовские множества и их свойства
3.2 Дисперсивность и сверхразрешимость факторизуемых
групп
Заключение
Список использованных источников
Введение
В теории конечных групп видное место занимают результаты,
связанные с исследованием существования дополнений к выделенным системам
подгрупп. В классических работах Шура, Цассенхауза, Гашюца, Л.А. Шеметкова
устанавливаются условия, при которых существует дополнение к нормальной
подгруппе. В 1968 году в работе для получения существования дополнений к
нормальной подгруппе Л.А. Шеметков стал рассматривать добавления. В
настоящее время под минимальным добавлением к подгруппе ![]() в группе
в группе ![]() понимается такая подгруппа
понимается такая подгруппа
![]() , что
, что ![]() , но
, но ![]() для любой собственной
подгруппы
для любой собственной
подгруппы ![]() из
из ![]() . Очевидно, что любая
подгруппа конечной группы обладает минимальным добавлением. Ясно также, что
дополнение является частным случаем минимального добавления.
. Очевидно, что любая
подгруппа конечной группы обладает минимальным добавлением. Ясно также, что
дополнение является частным случаем минимального добавления.
Известно, что конечные разрешимые группы можно охарактеризовать
как конечные группы, у которых дополняемы все силовские подгруппы. Эта теорема Ф. Холла
явилась источником развития одного из направлений теории групп, состоящего в
исследовании строения групп с выделенными системами дополняемых подгрупп. Как
отмечает в своей монографии С.Н. Черников: «Изучение групп с достаточно
широкой системой дополняемых подгрупп обогатило теорию групп многими важными
результатами». К настоящему времени выделены и полностью изучены многие новые
классы групп. При этом наметилась тенденция к обобщениям как самого понятия
дополняемой подгруппы, так и способа выделения системы дополняемых подгрупп.
Системы дополняемых подгрупп выделялись, например, с помощью таких понятий как
примарность, абелевость, цикличность, нормальность и других свойств конечных
групп и их комбинаций, а вместо дополняемости рассматривались ![]() –дополняемость,
–дополняемость, ![]() –плотность подгруппа,
строго содержащаяся между ними), и др.
–плотность подгруппа,
строго содержащаяся между ними), и др.
Однако условие существования дополнений к отдельным подгруппам является достаточно сильным ограничением. Далеко не все подгруппы обладают дополнениями. Вместе с тем каждая подгруппа обладает минимальным добавлением. Поэтому для исследования строения конечных групп с системами добавляемых подгрупп необходимо вводить дополнительные ограничения на минимальные добавления.
Квазинормальной называют подгруппу
![]() группы
группы ![]() , которая перестановочна со
всеми подгруппами группы
, которая перестановочна со
всеми подгруппами группы ![]() . Ясно,
что нормальные подгруппы всегда квазинормальны.
. Ясно,
что нормальные подгруппы всегда квазинормальны.
Минимальное добавление ![]() к
квазинормальной подгруппе
к
квазинормальной подгруппе ![]() группы
группы ![]() обладает следующим
свойством: если
обладает следующим
свойством: если ![]() – подгруппа из
– подгруппа из ![]() , то
, то ![]() – подгруппа группы
– подгруппа группы ![]() . Это наблюдение позволяет
ввести следующее определение: минимальное добавление
. Это наблюдение позволяет
ввести следующее определение: минимальное добавление ![]() к подгруппе
к подгруппе ![]() группы
группы ![]() назовём супердобавлением,
если
назовём супердобавлением,
если ![]() является подгруппой для
любой подгруппы
является подгруппой для
любой подгруппы ![]() из
из ![]() . Ясно, что нормальные и
квазинормальные подгруппы обладают супердобавлениями. В симметрической группе
. Ясно, что нормальные и
квазинормальные подгруппы обладают супердобавлениями. В симметрической группе ![]() силовская
силовская ![]() –подгруппа обладает
супердобавлением, но не является квазинормальной подгруппой. Кроме того, не
каждая подгруппа группы обладает супердобавлением.
–подгруппа обладает
супердобавлением, но не является квазинормальной подгруппой. Кроме того, не
каждая подгруппа группы обладает супердобавлением.
Всякую факторизуемую группу ![]() можно
рассматривать как группу с подгруппой
можно
рассматривать как группу с подгруппой ![]() и
её добавлением
и
её добавлением ![]() , и как группу с
подгруппой
, и как группу с
подгруппой ![]() и её добавлением
и её добавлением ![]() . Известно, что группа
. Известно, что группа ![]() с нормальными
сверхразрешимыми подгруппами
с нормальными
сверхразрешимыми подгруппами ![]() и
и ![]() не всегда является
сверхразрешимой. Отсюда следует, что формация всех сверхразрешимых групп не
является классом Фиттинга. Известны следующие случаи, ведущие к
сверхразрешимости группы
не всегда является
сверхразрешимой. Отсюда следует, что формация всех сверхразрешимых групп не
является классом Фиттинга. Известны следующие случаи, ведущие к
сверхразрешимости группы ![]() с
нормальными сверхразрешимыми подгруппами
с
нормальными сверхразрешимыми подгруппами ![]() и
и
![]() :
:
– подгруппы ![]() и
и ![]() имеют взаимно простые
индексы;
имеют взаимно простые
индексы;
– группа ![]() имеет
нильпотентный коммутант;
имеет
нильпотентный коммутант;
– подгруппы из ![]() перестановочны
со всеми подгруппами из
перестановочны
со всеми подгруппами из ![]() , а
подгруппы из
, а
подгруппы из ![]() перестановочны со всеми
подгруппами из
перестановочны со всеми
подгруппами из ![]() . Подобная
тематика разрабатывалась и в статье А.Ф. Васильева и Т.И. Васильевой.
. Подобная
тематика разрабатывалась и в статье А.Ф. Васильева и Т.И. Васильевой.
В настоящей дипломной работе рассматриваются следующие вопросы: строение группы с максимальной полунормальной подгруппой и группы с полунормальной силовской подгруппой; признаки дисперсивности и сверхразрешимости факторизуемых групп с перестановочными циклическими подгруппами в факторах.
1. Силовские подгруппы конечных групп
По теореме Лагранжа порядок каждой группы делит порядок конечной
группы. Обратное утверждение не всегда верно, т.е. если натуральное число ![]() делит порядок конечной
группы
делит порядок конечной
группы ![]() , то в группе
, то в группе ![]() может и не быть подгруппы
порядка
может и не быть подгруппы
порядка ![]() .
.
Пример 1.1 Знакопеременная группа ![]() порядка
12 не содержит подгруппу порядка 6.
порядка
12 не содержит подгруппу порядка 6.
Допустим противное, пусть ![]() –
подгруппа порядка 6 в группе
–
подгруппа порядка 6 в группе ![]() . Тогда
. Тогда ![]() и
и ![]() . Группа
. Группа ![]() содержит подгруппы
содержит подгруппы
![]()
Если ![]() , то
, то ![]() и
и ![]() , противоречие. Поэтому
, противоречие. Поэтому ![]() , а т. к.
, а т. к. ![]() , то
, то ![]() . Противоречие. Поэтому
допущение не верно и группа
. Противоречие. Поэтому
допущение не верно и группа ![]() не
содержит подгруппу порядка 6.
не
содержит подгруппу порядка 6.
Вполне естественно возниает вопрос: для каких делителей ![]() порядка конечной группы
имеется подгруппа порядка
порядка конечной группы
имеется подгруппа порядка ![]() .
.
Положительный ответ на этот вопросв случае, когда ![]() – степень простого числа,
даёт теорема Силова. Для доказательства теоремы Силова потребуется следующая
лемма.
– степень простого числа,
даёт теорема Силова. Для доказательства теоремы Силова потребуется следующая
лемма.
Лемма 1.2 Если порядок конечной абелевой группы ![]() делится на простое число
делится на простое число ![]() , то в группе
, то в группе ![]() существует элемент порядка
существует элемент порядка
![]() .
.
Доказательство. Предположим противное, т.е. допустим, что
существует абелева группа ![]() порядка
порядка
![]() , простое число
, простое число ![]() делит
делит ![]() , то в группе
, то в группе ![]() существует элемент порядка
существует элемент порядка
![]() . Пусть
. Пусть ![]() .
.
Если ![]() делит
делит ![]() для некоторого
для некоторого ![]() , то
, то ![]() – элемент порядка
– элемент порядка ![]() , противоречие. Поэтому все
элементы группы
, противоречие. Поэтому все
элементы группы ![]() имеют порядки,
не делящиеся на
имеют порядки,
не делящиеся на ![]() .
.
![]()
не делится на ![]() .
.
Так как группа ![]() абелева,
то
абелева,
то ![]() – подгруппа, и к
произведению
– подгруппа, и к
произведению ![]() можно применить следующее
можно применить следующее
![]()
не делится на ![]() .
.
Затем ![]() обозначаем через
обозначаем через
![]() и опять получаем, что
и опять получаем, что ![]() не делится на
не делится на ![]() . Через конечное число
шагов приходим к выводу, что
. Через конечное число
шагов приходим к выводу, что ![]() не
делится на
не
делится на ![]() . Но
. Но
![]()
и ![]() , т.е. получаем,
что
, т.е. получаем,
что ![]() не делит
не делит ![]() . Противоречие. Значит,
допущение неверно и лемма спарведлива.
. Противоречие. Значит,
допущение неверно и лемма спарведлива.
Пусть ![]() – простое число.
– простое число.
![]() - Группой называют
конечную группу, порядок которой есть степень числа
- Группой называют
конечную группу, порядок которой есть степень числа ![]() .
Конечная группа называется примарной, если она является
.
Конечная группа называется примарной, если она является ![]() -группой для некоторого
простого
-группой для некоторого
простого ![]() .
.
Теорема 1.3 Ошибка!. Пусть конечная группа ![]() имеет порядок
имеет порядок ![]() , где
, где ![]() – простое число и
– простое число и ![]() не делит
не делит ![]() . Тогда спарведливы
следующие утверждения:
. Тогда спарведливы
следующие утверждения:
в группе ![]() существует
подгруппа порядка
существует
подгруппа порядка ![]() для каждого
для каждого ![]() ;
;
если ![]() –
– ![]() -подгруппа группы
-подгруппа группы ![]() и
и ![]() – подгруппа порядка
– подгруппа порядка ![]() , то существует такой элемент
, то существует такой элемент
![]() , что
, что ![]() ;
;
любые две подгруппы порядка ![]() сопряжены
в группе
сопряжены
в группе ![]() ;
;
число подгрупп порядка ![]() в
группе
в
группе ![]() сравнимо с единицей по
модулю
сравнимо с единицей по
модулю ![]() и делит
и делит ![]() .
.
Доказательство. Доказательство проведём индукцией по ![]() . По индукции считаем, что
для всех групп, порядок которых меньше порядка
. По индукции считаем, что
для всех групп, порядок которых меньше порядка ![]() утверждение
теоремы выполняется. Рассмотрим два случая.
утверждение
теоремы выполняется. Рассмотрим два случая.
Случай 1. Порядок центра ![]() делится
на
делится
на ![]() .
.
Так как ![]() – абелева
группа, то к
– абелева
группа, то к ![]() применима лемма 1.2. По
этой лемме в
применима лемма 1.2. По
этой лемме в ![]() есть элемент
есть элемент ![]() порядка
порядка ![]() . Так как
. Так как ![]() – нормальная подгруппа
группы
– нормальная подгруппа
группы ![]() порядка
порядка ![]() , то факторгруппа
, то факторгруппа ![]() имеет порядок
имеет порядок ![]() и по индукции в группе
и по индукции в группе ![]() имеется подгруппа
имеется подгруппа ![]() порядка
порядка ![]() для каждого
для каждого ![]() . По теореме о соответствии
в группе
. По теореме о соответствии
в группе ![]() имеется подгруппа
имеется подгруппа ![]() такая, что
такая, что ![]() и
и ![]() . Теперь
. Теперь ![]() , где
, где ![]() . Итак, в группе
. Итак, в группе ![]() порядков
порядков ![]() соответственно.
соответственно.
Случай 2. Порядок центра ![]() группы
группы
![]() не делится на
не делится на ![]() .
.
Рассмотрим разложение группы ![]() в
объдинение различных классов сопряжённых элементов
в
объдинение различных классов сопряжённых элементов
![]()
где
![]()
– класс сопряжённых с ![]() элементов.
Различные классы сопряжённых элементов имеют пустое пересечение, а число
элементов в классе
элементов.
Различные классы сопряжённых элементов имеют пустое пересечение, а число
элементов в классе ![]() равно индексу
централизатора
равно индексу
централизатора ![]() . Пусть
. Пусть
![]()
Централизатор каждого элемента из центра совпадает с группой ![]() . И обратно, если
централизатор некоторого элемента совпадает с группой, то элемент попадает в
центр
. И обратно, если
централизатор некоторого элемента совпадает с группой, то элемент попадает в
центр ![]() . Поэтому из <1>
получаем
. Поэтому из <1>
получаем
![]()
где ![]() для каждого
для каждого ![]() . Если все числа
. Если все числа ![]() делятся на
делятся на ![]() , то из <2> следует,
что
, то из <2> следует,
что ![]() делится на
делится на ![]() , что противоречит
рассматриваемому случаю. Итак, существует
, что противоречит
рассматриваемому случаю. Итак, существует ![]() ,
где
,
где ![]() такое, что
такое, что ![]() не делит
не делит ![]() . Поскольку
. Поскольку ![]() то
то
![]()
где ![]() – целое число и
– целое число и ![]() не делит
не делит ![]() . Теперь к группе
. Теперь к группе ![]() применима индукция. По
индукции в группе
применима индукция. По
индукции в группе ![]() существует
подгруппа порядка
существует
подгруппа порядка ![]() для каждого
для каждого ![]() Эта подгруппа будет
искомой для группы
Эта подгруппа будет
искомой для группы ![]() .
.
Рассмотрим разложение группы ![]() на
двойные смежные классы по подгруппам
на
двойные смежные классы по подгруппам ![]() и
и ![]() :
:
![]()
Зададим отображение
![]()
переводящее элементы двойного смежного класса ![]() в элементы произведения
подгрупп
в элементы произведения
подгрупп ![]() и
и ![]() . Легко проверить, что
отоюражение
. Легко проверить, что
отоюражение ![]() взаимно однозначно,
поэтому, получаем
взаимно однозначно,
поэтому, получаем
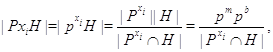
где ![]() Так как
Так как ![]() есть подгруппа в
есть подгруппа в ![]() , то по теореме Лагранжа
, то по теореме Лагранжа ![]() делит
делит ![]() и
и ![]() – целое число. Из
<3> теперь получаем:
– целое число. Из
<3> теперь получаем:
![]()
Сокращая обе части на ![]() получим:
получим:
![]()
Так как ![]() взаимно просто с
взаимно просто с
![]() , а
, а ![]() – целое число, являющееся
степенью
– целое число, являющееся
степенью ![]() , то в правой части
<4> существует слагаемое, равное единице. Пусть например,
, то в правой части
<4> существует слагаемое, равное единице. Пусть например, ![]() , где
, где ![]() . Тогда
. Тогда ![]() .
.
Пусть ![]() и
и ![]() – подгруппы порядка
– подгруппы порядка ![]() . По существует элемент
. По существует элемент ![]() такой, что
такой, что ![]() . Так как
. Так как ![]() , то
, то ![]() .
.
Пусть ![]() – группа порядка
– группа порядка
![]() – подгруппа порядка
– подгруппа порядка ![]() и
и ![]() – нормализатор подгруппы
– нормализатор подгруппы ![]() в группе
в группе ![]() . Рассмотрим разложение
группы
. Рассмотрим разложение
группы ![]() на двойные смежные классы
по
на двойные смежные классы
по ![]() и
и ![]() :
:
![]()
Отображение
![]()
будет взаимно однозначным отображением ![]() на
на
![]() . Теперь из <5>
получаем:
. Теперь из <5>
получаем:
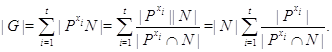
Положим ![]() . Элемент
. Элемент ![]() можно выбрать единичным,
поэтому
можно выбрать единичным,
поэтому ![]() и
и ![]() . Теперь
. Теперь
![]()
Проверим, что под знаком суммы нет слагаемых равных 1. Допустим
противное, т.е. что для некоторого ![]() имеем
равенство
имеем
равенство ![]() . Это означает, что
. Это означает, что ![]() и подгруппа
и подгруппа ![]() содержит две подгруппы
содержит две подгруппы ![]() и
и ![]() порядка
порядка ![]() . По существует элемент
. По существует элемент ![]() такой, что
такой, что ![]() . Но тогда
. Но тогда ![]() , а так как
, а так как ![]() , то и
, то и ![]() . Но это возможно только
при
. Но это возможно только
при ![]() , противоречие. Значит,
допущение неверно и в равенстве <6> под знаком суммы все слагаемые
отличны от единицы. Поскольку каждое слагаемое есть степень простого
, противоречие. Значит,
допущение неверно и в равенстве <6> под знаком суммы все слагаемые
отличны от единицы. Поскольку каждое слагаемое есть степень простого ![]() , то из равенства <6>
получаем сравнение
, то из равенства <6>
получаем сравнение ![]()
![]() . По все подгруппы порядка
. По все подгруппы порядка ![]() группы
группы ![]() сопряжены между собой, а
число подгрупп сопряжённых с
сопряжены между собой, а
число подгрупп сопряжённых с ![]() равно
равно ![]() . Поскольку
. Поскольку ![]() , то
, то ![]() делит
делит ![]() .
.
Теорема доказана.
Силовской ![]() – подгруппой конечной группы
– подгруппой конечной группы ![]() называют
такую
называют
такую ![]() – подгруппу, индекс
которой не делится на
– подгруппу, индекс
которой не делится на ![]() . Непосредственно
из теоремы получаем
. Непосредственно
из теоремы получаем
Следствие 1.4 Пусть конечная группа ![]() имеет
порядок
имеет
порядок ![]() , где
, где ![]() – простое число и
– простое число и ![]() не делит
не делит ![]() . Тогда:
. Тогда:
существует силовская ![]() –подгруппа
и её порядок равен
–подгруппа
и её порядок равен ![]() ;
;
каждая ![]() –подгруппа
содержится в некоторой силовской
–подгруппа
содержится в некоторой силовской ![]() –подгруппе;
–подгруппе;
любые две силовские ![]() –подгруппы
сопряжены;
–подгруппы
сопряжены;
число силовских ![]() –подгрупп
сравнимо с единицей по модулю
–подгрупп
сравнимо с единицей по модулю ![]() и делит
и делит
![]() .
.
Теорема 1.5 Для конечной группы ![]() и
её силовской
и
её силовской ![]() –подгруппы
–подгруппы ![]() справедливы следующие
утверждения:
справедливы следующие
утверждения:
если ![]() , то
, то ![]() – силовская
– силовская ![]() –подгруппа в
–подгруппа в ![]() , а
, а ![]() – силовская
– силовская ![]() –подгрупппа в
–подгрупппа в ![]() ;
;
![]() ;
;
если ![]() и
и ![]() , то
, то
![]()
и
![]()
пусть ![]() – все простые
делители порядка группы
– все простые
делители порядка группы ![]() ,
, ![]() при
при ![]() , и пусть
, и пусть ![]() – соответствующие им
силовские подгруппы. Тогда
– соответствующие им
силовские подгруппы. Тогда
![]()
а если ![]() , то
, то ![]() .
.
Д о к а з а т.е. л ь с т в о. Так как ![]() и
и
![]() не делит
не делит ![]() , то
, то ![]() –
– ![]() –группа, а из того, что
–группа, а из того, что
![]()
следует
![]()
![]()
и ![]() не делится на
не делится на ![]() . Значит
. Значит ![]() – силовская
– силовская ![]() –подгруппа в
–подгруппа в ![]() .
.
Поскольку ![]() , то
, то ![]() –
– ![]() –группа, а так как
–группа, а так как
![]()
не делится на ![]() , то
, то ![]() – силовская
– силовская ![]() –подгруппа в
–подгруппа в ![]() .
.
Для ![]() получаем
получаем
![]()
т.е. ![]() . Обратно, если
. Обратно, если ![]() , то
, то ![]() . Теперь
. Теперь ![]() и
и ![]() – силовские подгруппы в
– силовские подгруппы в ![]() , которые по следствию 1.4
сопряжены в
, которые по следствию 1.4
сопряжены в ![]() , т.е. существует элемент
, т.е. существует элемент ![]() , такой, что
, такой, что ![]() . Теперь
. Теперь ![]() и
и ![]() , т.е.
, т.е.
![]()
Если
![]()
то ![]() и
и
![]()
Если ![]() , то пусть
, то пусть ![]() означает наивысшую степень
означает наивысшую степень
![]() , делящую порядок
, делящую порядок ![]() . По следствию 1.4
. По следствию 1.4 ![]() – порядок силовской
– порядок силовской ![]() –подгруппы из
–подгруппы из ![]() . Из следует, что
. Из следует, что
![]()
и
![]()
Если
![]()
то
![]()
и
![]()
Обратно, пусть
![]()
где ![]() ,
, ![]() и
и ![]() . Тогда
. Тогда
![]()
Поскольку уже доказано, что
![]()
то ![]() , где
, где
![]()
Теперь
![]()
и
![]()
Следовательно,
![]()
Пусть
![]()
Тогда ![]() делит
делит ![]() для каждого
для каждого ![]() и поэтому
и поэтому
![]()
делит ![]() , т.е.
, т.е. ![]() . Для
. Для ![]() имеем
имеем ![]() , откуда
, откуда ![]() .
.
Теорема доказана.
Лемма 1.6 Ошибка!. Если ![]() –
нормальная подгруппа конечной группы
–
нормальная подгруппа конечной группы ![]() и
и ![]() – силовская
– силовская ![]() – подгруппа из
– подгруппа из ![]() , то
, то ![]() .
.
Доказательство. Пусть ![]() –
произвольный элемент из
–
произвольный элемент из ![]() . Так
как
. Так
как ![]() , то
, то ![]() и по следствию 1.4
подгруппы
и по следствию 1.4
подгруппы ![]() и
и ![]() сопряжены в
сопряжены в ![]() . Поэтому, существует
элемент
. Поэтому, существует
элемент ![]() такой, что
такой, что ![]() , откуда
, откуда
![]()
и
![]()
Таким образом, ![]() .
.
Лемма доказана.
Лемма 1.7 Каждая подгруппа конечной группы, содержащая нормализатор некоторой силовской подгруппы, самонормализуема.
Доказательство. Пусть ![]() –
силовская подгруппа группы
–
силовская подгруппа группы ![]() и
и ![]() – подгруппа группы
– подгруппа группы ![]() , содержащая
, содержащая ![]() . Так как
. Так как ![]() , то по лемме Фраттини
, то по лемме Фраттини
![]()
Лемма доказана.
Лемма 1.8 Пусть ![]() –
– ![]() –подгруппа конечной группы
–подгруппа конечной группы ![]() ,
, ![]() и
и ![]() не делит
не делит ![]() . Тогда
. Тогда
![]()
Доказательство. Ясно, что
![]()
По условию подгруппа ![]() является
силовской подгруппой в
является
силовской подгруппой в ![]() . Пусть
. Пусть
![]()
Тогда ![]() и по лемме
Фраттини
и по лемме
Фраттини ![]() .
.
Лемма доказана.
Пример 1.9 Симметрическая группа ![]() степени
6 имеет порядок
степени
6 имеет порядок ![]() . По теореме
Силова
. По теореме
Силова ![]() содержит подгруппы
порядков
содержит подгруппы
порядков ![]() . Силовская 2‑подгруппа
имеет порядок
. Силовская 2‑подгруппа
имеет порядок ![]() , силовская 3‑подгруппа
имеет порядок
, силовская 3‑подгруппа
имеет порядок ![]() и силовская 5‑подгруппа
имеет порядок 5.
и силовская 5‑подгруппа
имеет порядок 5.
Пример 1.10 Группа порядка 15 циклическая.
Пусть ![]() – группа порядка
15. В группе
– группа порядка
15. В группе ![]() имеется подгруппа
имеется подгруппа ![]() порядка 3 и подгруппа
порядка 3 и подгруппа ![]() порядка 5. По следствию
1.4 число силовских 3‑подгрупп имеет вид
порядка 5. По следствию
1.4 число силовских 3‑подгрупп имеет вид ![]() для
некоторого неотрицательного целого
для
некоторого неотрицательного целого ![]() и делит
5. Поэтому в группе имеется только одна подгруппа порядка 3. Так как любые две
силовские 3‑подгруппы сопряжены, то
и делит
5. Поэтому в группе имеется только одна подгруппа порядка 3. Так как любые две
силовские 3‑подгруппы сопряжены, то ![]() .
Аналогично, число силовских 5‑подгрупп равно
.
Аналогично, число силовских 5‑подгрупп равно ![]() и
делит 3. Поэтому
и
делит 3. Поэтому ![]() . Так как
. Так как ![]() и
и ![]() – циклические подгруппы
простых порядков, то группа
– циклические подгруппы
простых порядков, то группа ![]() . Теперь
для любых
. Теперь
для любых ![]() имеем:
имеем:
![]()
![]()
поэтому
![]()
и ![]() . Следовательно,
группа
. Следовательно,
группа ![]() абелева. Теперь ясно, что
абелева. Теперь ясно, что ![]() – циклическая группа.
– циклическая группа.
2. Полунормальные подгруппы
2.1 Свойства супердобавлений
Определение 2.1.1 Подгруппу, обладающую супердобавлением, называют
полунормальной подгруппой. Таким образом, подгруппа ![]() группы
группы ![]() называется полунормальной
подгруппой, если существует такая подгруппа
называется полунормальной
подгруппой, если существует такая подгруппа ![]() ,
что
,
что ![]() и
и ![]() – собственная подгруппа
группы
– собственная подгруппа
группы ![]() для каждой подгруппы
для каждой подгруппы ![]() из
из ![]() , отличной от
, отличной от ![]() .
.
Пример 2.1.2 Нормальные и квазинормальные подгруппы являются полунормальными и любые их минимальные добавления будут супердобавлениями.
Пример 2.1.3 В симметрической группе ![]() силовская
силовская
![]() –подгруппа является
полунормальной подгруппой, но не квазинормальной.
–подгруппа является
полунормальной подгруппой, но не квазинормальной.
Лемма 2.1.4 Если подгруппа ![]() полунормальна
в группе
полунормальна
в группе ![]() и в группе
и в группе ![]() нет собственных добавлений
к
нет собственных добавлений
к ![]() , то
, то ![]() квазинормальна.
квазинормальна.
Доказательство. Так как по условию все добавления к подгруппе ![]() совпадают с самой группой
совпадают с самой группой ![]() , то и супердобавлением к
, то и супердобавлением к ![]() будет
будет ![]() . Теперь из определения
полунормальной подгруппы следует, что
. Теперь из определения
полунормальной подгруппы следует, что ![]() перестановочна
со всеми собственными подгруппами группы
перестановочна
со всеми собственными подгруппами группы ![]() .
.
Лемма доказана.
Введем следующие обозначения. Если ![]() –
подгруппа группы
–
подгруппа группы ![]() , то
, то ![]() – множество всех
супердобавлений к подгруппе
– множество всех
супердобавлений к подгруппе ![]() в
группе
в
группе ![]() . Ясно, что
. Ясно, что ![]() в точности тогда, когда
в точности тогда, когда ![]() не является полунормальной
подгруппой.
не является полунормальной
подгруппой.
Пусть ![]() и
и ![]() – подгруппы группы
– подгруппы группы ![]() ,
, ![]() и подгруппа
и подгруппа ![]() нормальна в группе
нормальна в группе ![]() . Введём следующие
обозначения:
. Введём следующие
обозначения:
![]()
![]() –
обычное теоретико множественное включение, то есть любая группа
–
обычное теоретико множественное включение, то есть любая группа ![]() содержится в
содержится в ![]() .
.
Запись
![]()
означает, что для любой подгруппы ![]() существует
подгруппа
существует
подгруппа ![]() такая, что
такая, что ![]() содержится в
содержится в ![]() .
.
![]()
![]()
Лемма 2.1.5 Если ![]() –
полунормальная подгруппа группы
–
полунормальная подгруппа группы ![]() и
и ![]() , то
, то ![]() – полунормальная подгруппа
группы
– полунормальная подгруппа
группы ![]() и
и
![]()
Доказательство. Пусть ![]() . Тогда
. Тогда ![]() и
и ![]() – собственная подгруппа
группы
– собственная подгруппа
группы ![]() для любой подгруппы
для любой подгруппы ![]() из
из ![]() , отличной от
, отличной от ![]() . Ясно, что
. Ясно, что ![]() для любого элемента
для любого элемента ![]() из
из ![]() , а так как
, а так как ![]() можно считать произвольной
в
можно считать произвольной
в ![]() подгруппой, отличной от
подгруппой, отличной от ![]() , то
, то ![]() – собственная подгруппа
группы
– собственная подгруппа
группы ![]() . Поэтому
. Поэтому ![]() полунормальна в
полунормальна в ![]() и
и ![]() – супердобавление к
– супердобавление к ![]() в группе
в группе ![]() , то есть
, то есть ![]() . Отсюда следует, что
. Отсюда следует, что ![]() . Группа
. Группа ![]() для любого
для любого ![]() . Так как
. Так как ![]() , то
, то ![]() , где
, где ![]() ,
, ![]() . Теперь
. Теперь ![]() . Если
. Если ![]() – подгруппа из
– подгруппа из ![]() , отличная от
, отличная от ![]() , то
, то ![]() – подгруппа из
– подгруппа из ![]() , отличная от
, отличная от ![]() . Поэтому
. Поэтому ![]() – собственная подгруппа
группы
– собственная подгруппа
группы ![]() и
и ![]() . Значит,
. Значит, ![]() для всех
для всех ![]() . Отсюда следует, что
. Отсюда следует, что ![]() .
.
Лемма доказана.
Лемма 2.1.6 Если ![]() –
полунормальная подгруппа группы
–
полунормальная подгруппа группы ![]() и
и ![]() – подгруппа, содержащая
– подгруппа, содержащая ![]() , то
, то ![]() полунормальна в
полунормальна в ![]() и для любой подгруппы
и для любой подгруппы ![]() пересечение
пересечение ![]() содержит супердобавление к
подгруппе
содержит супердобавление к
подгруппе ![]() в
в ![]() .
.
Доказательство. Пусть ![]() полунормальна
в
полунормальна
в ![]() и
и ![]() . Так как
. Так как ![]() , то по тождеству Дедекинда
имеем
, то по тождеству Дедекинда
имеем ![]() . Пусть
. Пусть ![]() – наименьшая подгруппа из
– наименьшая подгруппа из ![]() , для которой
, для которой ![]() . Если
. Если ![]() – собственная подгруппа из
– собственная подгруппа из
![]() , то
, то ![]() . Поскольку
. Поскольку ![]() , то
, то ![]() – подгруппа группы
– подгруппа группы ![]() , поэтому
, поэтому ![]() полунормальна в
полунормальна в ![]() и
и ![]() – супердобавление в
– супердобавление в ![]() .
.
Лемма доказана.
Лемма 2.1.7 Если ![]() –
полунормальная подгруппа группы
–
полунормальная подгруппа группы ![]() и
и ![]() , то
, то ![]() – полунормальная подгруппа
группы
– полунормальная подгруппа
группы ![]() и любая группа из
и любая группа из ![]() содержит супердобавление к
содержит супердобавление к
![]() в
в ![]() .
.
Доказательство. Пусть ![]() полунормальна
в
полунормальна
в ![]() и
и ![]() . Тогда
. Тогда ![]() . Пусть
. Пусть ![]() – наименьшая подгруппа из
– наименьшая подгруппа из ![]() такая, что
такая, что ![]() . Выберем произвольную
подгруппу
. Выберем произвольную
подгруппу ![]() из
из ![]() , отличную от
, отличную от ![]() . Так как
. Так как ![]() , то
, то ![]() . Поскольку
. Поскольку ![]() , то по тождеству Дедекинда
, то по тождеству Дедекинда
![]() . Теперь
. Теперь ![]() , а из полунормальности
, а из полунормальности ![]() следует, что
следует, что ![]() – подгруппа группы
– подгруппа группы ![]() и
и ![]() – собственная подгруппа
группы
– собственная подгруппа
группы ![]() . Это означает, что
. Это означает, что ![]() полунормальна в
полунормальна в ![]() и
и ![]() . Так как
. Так как ![]() , то лемма доказана.
, то лемма доказана.
Лемма 2.1.8 Пусть ![]() –
полунормальная подгруппа группы
–
полунормальная подгруппа группы ![]() и
и ![]() . Если
. Если ![]() – полунормальная подгруппа
группы
– полунормальная подгруппа
группы ![]() , то
, то ![]() – полунормальная подгруппа
группы
– полунормальная подгруппа
группы ![]() и
и ![]() .
.
Доказательство. По условию ![]() и
и
![]() , где
, где ![]() . Кроме того,
. Кроме того, ![]() – подгруппа группы
– подгруппа группы ![]() . Ясно, что
. Ясно, что ![]() . Если
. Если ![]() – собственная подгруппа в
– собственная подгруппа в ![]() , то
, то ![]() – собственная подгруппа в
– собственная подгруппа в ![]() и
и ![]() . Ясно, что
. Ясно, что ![]() и
и ![]() перестановочны с
перестановочны с ![]() , поэтому
, поэтому ![]() . Так как
. Так как ![]() , то
, то ![]() . Значит,
. Значит, ![]() является супердобавлением
к
является супердобавлением
к ![]() в
в ![]() , то есть
, то есть ![]() , что и требовалось
доказать.
, что и требовалось
доказать.
Лемма 2.1.9 Если ![]() –
подгруппа группы
–
подгруппа группы ![]() и
и ![]() – её минимальное
добавление, то следующие утверждения эквивалентны:
– её минимальное
добавление, то следующие утверждения эквивалентны:
![]() полунормальна
в группе
полунормальна
в группе ![]() и
и ![]() ;
;
для каждого элемента ![]() и
каждого элемента
и
каждого элемента ![]() существуют целое
число
существуют целое
число ![]() и элемент
и элемент ![]() такие, что
такие, что ![]() .
.
Доказательство. ![]() . Пусть
подгруппа
. Пусть
подгруппа ![]() полунормальна в группе
полунормальна в группе ![]() и
и ![]() – ее супердобавление.
Подгруппа
– ее супердобавление.
Подгруппа ![]() , где
, где ![]() пробегает все элементы
группы
пробегает все элементы
группы ![]() , причем
, причем ![]() – подгруппа группы
– подгруппа группы ![]() , что следует из
полунормальности
, что следует из
полунормальности ![]() . Поэтому
. Поэтому ![]() . Теперь выбираем
произвольные элемент
. Теперь выбираем
произвольные элемент ![]() и элемент
и элемент ![]() . В силу того, что
. В силу того, что ![]() получаем, что
получаем, что ![]() для некоторого целого
числа
для некоторого целого
числа ![]() и некоторого элемента
и некоторого элемента ![]() .
.
![]() .
Пусть для каждого элемента
.
Пусть для каждого элемента ![]() и
каждого элемента
и
каждого элемента ![]() существуют целое
число
существуют целое
число ![]() и элемент
и элемент ![]() такие, что
такие, что ![]() . Так как из равенства
. Так как из равенства ![]() вытекает включение
вытекает включение ![]() , а из равенства
, а из равенства ![]() следует, что
следует, что ![]() , значит
, значит ![]() . Ввиду того, что для любой
подгруппы
. Ввиду того, что для любой
подгруппы ![]() из
из ![]() имеем
имеем ![]() , где
, где ![]() , то получаем равенство
, то получаем равенство ![]() . Это означает, что
. Это означает, что ![]() полунормальна в
полунормальна в ![]() и
и ![]() .
.
Лемма доказана.
Лемма 2.1.10 Пусть ![]() ,
подгруппа
,
подгруппа ![]() нормальна в группе
нормальна в группе ![]() . Подгруппа
. Подгруппа ![]() полунормальна в группе
полунормальна в группе ![]() тогда и только тогда,
когда подгруппа
тогда и только тогда,
когда подгруппа ![]() полунормальна в
группе
полунормальна в
группе ![]() .
.
Доказательство. Пусть подгруппа ![]() полунормальна
в группе
полунормальна
в группе ![]() . Тогда по лемме 2.1.7
подгруппа
. Тогда по лемме 2.1.7
подгруппа ![]() полунормальна в группе
полунормальна в группе ![]() .
.
Обратно, если ![]() полунормальна
в
полунормальна
в ![]() , то из определения
полунормальной подгруппы получаем, что существует подгруппа
, то из определения
полунормальной подгруппы получаем, что существует подгруппа ![]() из факторгруппы
из факторгруппы ![]() такая, что
такая, что ![]() и
и ![]() , где
, где ![]() . Откуда следует, что
. Откуда следует, что ![]() . Пусть
. Пусть ![]() – наименьшая подгруппа из
– наименьшая подгруппа из ![]() такая, что
такая, что ![]() и
и ![]() . Рассмотрим произвольную
собственную подгруппу
. Рассмотрим произвольную
собственную подгруппу ![]() из
из ![]() .
.
Если ![]() , то
, то ![]() – собственная подгруппа
группы
– собственная подгруппа
группы ![]() , поэтому
, поэтому ![]() – подгруппа группы
– подгруппа группы ![]() .
.
Если ![]() не содержит
не содержит ![]() , то
, то ![]() – подгруппа группы
– подгруппа группы ![]() и
и ![]() – подгруппа группы
– подгруппа группы ![]() . Это означает, что
. Это означает, что ![]() полунормальна в
полунормальна в ![]() и
и ![]() .
.
Лемма доказана.
Лемма 2.1.11 Пусть подгруппа ![]() полунормальна
в
полунормальна
в ![]() ,
, ![]() и
и ![]() . Тогда для любого
. Тогда для любого ![]() подгруппа
подгруппа ![]() перестановочна со всеми
сопряженными подгруппами
перестановочна со всеми
сопряженными подгруппами ![]() .
.
Доказательство. Если элемент ![]() ,
то
,
то ![]() , где
, где ![]() ,
, ![]() . Из полунормальности
подгруппы
. Из полунормальности
подгруппы ![]() вытекает, что
вытекает, что ![]() . Имеем
. Имеем ![]() . Поэтому
. Поэтому ![]() .
.
Лемма доказана.
Лемма 2.1.12 Произведение квазинормальной и полунормальной подгрупп является полунормальной подгруппой. В частности, произведение нормальной и полунормальной подгрупп есть полунормальная подгруппа.
Доказательство. Пусть ![]() –
квазинормальная подгруппа группы
–
квазинормальная подгруппа группы ![]() и
и ![]() – полунормальная подгруппа
с супердобавлением
– полунормальная подгруппа
с супердобавлением ![]() . Тогда
. Тогда ![]() и
и ![]() – собственная подгруппа
группы
– собственная подгруппа
группы ![]() для всех собственных
подгрупп
для всех собственных
подгрупп ![]() из
из ![]() . Пусть
. Пусть ![]() – наименьшая в
– наименьшая в ![]() подгруппа, для которой
подгруппа, для которой ![]() . Если
. Если ![]() , то
, то ![]() , а так как
, а так как ![]() – подгруппа группы
– подгруппа группы ![]() и
и ![]() квазинормальная, то
квазинормальная, то ![]() и
и ![]() есть подгруппа группы
есть подгруппа группы ![]() .
.
Лемма доказана.
2.2 Супердобавления к максимальным подгруппам
Теорема 2.2.1 Пусть ![]() –
максимальная подгруппа группы
–
максимальная подгруппа группы ![]() .
Подгруппа
.
Подгруппа ![]() обладает супердобавлением
в группе
обладает супердобавлением
в группе ![]() тогда и только тогда,
когда индекс
тогда и только тогда,
когда индекс ![]() в
в ![]() есть простое число.
есть простое число.
Доказательство. Необходимоcть. Пусть ![]() –
максимальная подгруппа группы
–
максимальная подгруппа группы ![]() и
и ![]() имеет супердобавление в
группе
имеет супердобавление в
группе ![]() , т.е. существует такая
подгруппа
, т.е. существует такая
подгруппа ![]() из
из ![]() , что
, что ![]() и
и ![]() есть собственная подгруппа
в
есть собственная подгруппа
в ![]() для каждой подгруппы
для каждой подгруппы ![]() из
из ![]() , отличной от
, отличной от ![]() . Пусть
. Пусть ![]() и
и ![]() – две различные
максимальные подгруппы в группе
– две различные
максимальные подгруппы в группе ![]() . Тогда
. Тогда ![]() и
и ![]() . Из максимальности
. Из максимальности ![]() следует, что
следует, что ![]() и
и ![]() являются подгруппами
являются подгруппами ![]() . Но тогда
. Но тогда ![]() , противоречие с тем, что
, противоречие с тем, что ![]() и
и ![]() – максимальная в
– максимальная в ![]() подгруппа. Следовательно,
в
подгруппа. Следовательно,
в ![]() имеется единственная
максимальная подгруппа
имеется единственная
максимальная подгруппа ![]() . Если
. Если ![]() , то циклическая подгруппа,
порожденная элементом
, то циклическая подгруппа,
порожденная элементом ![]() , не содержится в
, не содержится в
![]() , поэтому
, поэтому ![]() . Кроме того,
. Кроме того, ![]() – примарная группа, то
есть
– примарная группа, то
есть ![]() . Если
. Если ![]() – максимальная подгруппа в
– максимальная подгруппа в
![]() , то индекс
, то индекс ![]() в
в ![]() есть простое число
есть простое число ![]() и
и ![]() – подгруппа в
– подгруппа в ![]() . Поэтому,
. Поэтому, ![]() .
.
Достаточность. Пусть ![]() –
подгруппа группы
–
подгруппа группы ![]() и
и ![]() . Пусть
. Пусть ![]() – силовская
– силовская ![]() -подгруппа группы
-подгруппа группы ![]() . Тогда
. Тогда ![]() не содержится в
не содержится в ![]() и существует элемент
и существует элемент ![]() . Пусть
. Пусть ![]() ,
, ![]() . Ясно, что
. Ясно, что ![]() , поэтому
, поэтому
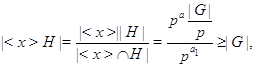
и ![]() . Теперь
. Теперь ![]() принадлежит
принадлежит ![]() , следовательно, если
, следовательно, если ![]() – собственная подгруппа
циклической группы
– собственная подгруппа
циклической группы ![]() , то
, то ![]() – подгруппа в
– подгруппа в ![]() и
и ![]() обладает супердобавлением
обладает супердобавлением ![]() в группе
в группе ![]() .
.
Теорема доказана.
Следствие 2.2.2 Группа сверхразрешима тогда и только тогда, когда все ее максимальные подгруппы имеют супердобавления.
Доказательство. Если ![]() –
сверхразрешимая группа, то все ее максимальные подгруппы имеют простые индексы.
По теореме 2.2.1 все максимальные подгруппы обладают супердобавлениями.
–
сверхразрешимая группа, то все ее максимальные подгруппы имеют простые индексы.
По теореме 2.2.1 все максимальные подгруппы обладают супердобавлениями.
Обратно, пусть все максимальные подгруппы имеют супердобавления.
По теореме 2.2.1 все они имеют простые индексы. Следовательно группа ![]() сверхразрешима.
сверхразрешима.
Следствие доказано.
Следствие 2.2.3 Пусть ![]() –
некоторое множество простых чисел. Если в
–
некоторое множество простых чисел. Если в ![]() -разрешимой
группе
-разрешимой
группе ![]() каждая максимальная
подгруппа, индекс которой делится на простое число из
каждая максимальная
подгруппа, индекс которой делится на простое число из ![]() , имеет супердобавление, то
, имеет супердобавление, то
![]() –
– ![]() -сверхразрешима.
-сверхразрешима.
Доказательство. По теореме 2.2.1 индекс каждой максимальной
подгруппы из ![]() либо
либо ![]() -число, либо равен
некоторому простому числу из
-число, либо равен
некоторому простому числу из ![]() . Группа
. Группа
![]()
![]() -сверхразрешима для всех
-сверхразрешима для всех ![]() . Поэтому
. Поэтому ![]()
![]() -сверхразрешима.
-сверхразрешима.
Следствие доказано.
Следствие 2.2.4 Если подгруппа ![]() имеет
супердобавление в группе
имеет
супердобавление в группе ![]() и
и ![]() – подгруппа группы, в
которой
– подгруппа группы, в
которой ![]() является максимальной
подгруппой, то
является максимальной
подгруппой, то ![]() – простое число.
– простое число.
Доказательство. По лемме 2.1.6 подгруппа ![]() обладает супердобавлением
в
обладает супердобавлением
в ![]() , а по теореме 2.2.1 индекс
, а по теореме 2.2.1 индекс
![]() в
в ![]() – простое число, что и
требовалось доказать.
– простое число, что и
требовалось доказать.
Следствие 2.2.5 В любой группе пересечение максимальных подгрупп, не обладающих супердобавлениями, является сверхразрешимой подгруппой.
Доказательство. Данное пересечение совпадает с пересечением максимальных подгрупп непростых индексов. Поэтому это пересечение сверхразрешимо.
Следствие доказано.
Пусть ![]() – формация всех
сверхразрешимых групп. Тогда
– формация всех
сверхразрешимых групп. Тогда ![]() – проектор
разрешимой группы
– проектор
разрешимой группы ![]() называется
сверхразрешимым проектором группы
называется
сверхразрешимым проектором группы ![]() или
подгруппой Гашюца. По теореме Гашюца в каждой разрешимой группе существует
единственный сопряженный класс сверхразрешимых проекторов. Кроме того, если
или
подгруппой Гашюца. По теореме Гашюца в каждой разрешимой группе существует
единственный сопряженный класс сверхразрешимых проекторов. Кроме того, если ![]() – сверхразрешимый проектор
разрешимой несверхразрешимой группы
– сверхразрешимый проектор
разрешимой несверхразрешимой группы ![]() и
и ![]() , то
, то ![]() – не простое число. Из
теоремы 2.2.1 получаем
– не простое число. Из
теоремы 2.2.1 получаем
Следствие 2.2.6 Сверхразрешимый проектор разрешимой группы обладает супердобавлением тогда и только тогда, когда он совпадает со всей группой.
Доказательство. Пусть ![]() –
разрешимая группа и
–
разрешимая группа и ![]() – ее
сверхразрешимый проектор. Предположим, что подгруппа
– ее
сверхразрешимый проектор. Предположим, что подгруппа ![]() обладает супердобавлением
в
обладает супердобавлением
в ![]() и
и ![]() . Пусть
. Пусть ![]() – подгруппа группы
– подгруппа группы ![]() , в которой
, в которой ![]() является максимальной подгруппой.
По лемме 2.1.6 подгруппа
является максимальной подгруппой.
По лемме 2.1.6 подгруппа ![]() полунормальна
в
полунормальна
в ![]() , а по следствию 2.2.4
индекс
, а по следствию 2.2.4
индекс ![]() – простое число. Но это
противоречит отмеченному свойству сверхразрешимого проектора. Поэтому
– простое число. Но это
противоречит отмеченному свойству сверхразрешимого проектора. Поэтому ![]() . Обратное утверждение
очевидно.
. Обратное утверждение
очевидно.
Следствие доказано.
Следствие 2.2.7 В разрешимой несверхразрешимой группе сверхразрешимый проектор не квазинормален.
Доказательство. Пусть группа ![]() и
и
![]() – ее сверхразрешимый
проектор. Если подгруппа
– ее сверхразрешимый
проектор. Если подгруппа ![]() полунормальна,
то по следствию 2.2.6 подгруппа
полунормальна,
то по следствию 2.2.6 подгруппа ![]() –
противоречие с выбором группы
–
противоречие с выбором группы ![]() .
Значит, подгруппа
.
Значит, подгруппа ![]() не
полунормальна, тем более не квазинормальна.
не
полунормальна, тем более не квазинормальна.
Следствие доказано.
2.3 Супердобавления к силовским подгруппам
Теорема 2.3.1 Пусть ![]() –
наибольший простой делитель порядка группы
–
наибольший простой делитель порядка группы ![]() и
и
![]() – ее силовская
– ее силовская ![]() -подгруппа. Если
-подгруппа. Если ![]() обладает супердобавлением
в
обладает супердобавлением
в ![]() , то
, то ![]() – нормальная подгруппа
группы
– нормальная подгруппа
группы ![]() .
.
Доказательство. Докажем вначале утверждение для бипримарных групп.
Пусть ![]() и
и ![]() – простые числа,
– простые числа, ![]() , и
, и ![]() – бипримарная группа, где
– бипримарная группа, где ![]() – силовская
– силовская ![]() -подгруппа, а
-подгруппа, а ![]() – силовская
– силовская ![]() -подгруппа. По условию
-подгруппа. По условию ![]() обладает супердобавлением
в
обладает супердобавлением
в ![]() , поэтому, можно считать,
что
, поэтому, можно считать,
что ![]() является этим
супердобавлением. Если
является этим
супердобавлением. Если ![]() и
и ![]() – различные максимальные
подгруппы группы
– различные максимальные
подгруппы группы ![]() , то из
полунормальности
, то из
полунормальности ![]() следует, что
следует, что ![]() и
и ![]() – собственные в
– собственные в ![]() подгруппы. По лемме 2.1.2
и по индукции получаем, что
подгруппы. По лемме 2.1.2
и по индукции получаем, что ![]() и
и ![]() . Поэтому
. Поэтому ![]() и
и ![]() нормальна в
нормальна в ![]() .
.
Пусть теперь в ![]() есть
единственная максимальная подгруппа. Тогда
есть
единственная максимальная подгруппа. Тогда ![]() –
циклическая примарная группа, а так как
–
циклическая примарная группа, а так как ![]() ,
то
,
то ![]() нормальна в
нормальна в ![]() .
.
Теперь рассмотрим произвольную группу ![]() .
По условию теоремы существует супердобавление
.
По условию теоремы существует супердобавление ![]() к
подгруппе
к
подгруппе ![]() в группе
в группе ![]() , где
, где ![]() – силовская
– силовская ![]() -подгруппа для наибольшего
делителя
-подгруппа для наибольшего
делителя ![]() порядка группы
порядка группы ![]() . То есть
. То есть ![]() и
и ![]() для любой собственной
подгруппы
для любой собственной
подгруппы ![]() из
из ![]() . Пусть
. Пусть ![]() – силовская
– силовская ![]() -подгруппа из
-подгруппа из ![]() для
для ![]() . Ясно, что
. Ясно, что ![]() силовская в
силовская в ![]() . Так как
. Так как ![]() – бипримарная подгруппа, в
которой
– бипримарная подгруппа, в
которой ![]() полунормальна, по
доказанному выше
полунормальна, по
доказанному выше ![]() . Из того, что
. Из того, что ![]() – любое простое число,
отличное от
– любое простое число,
отличное от ![]() , получаем, что
, получаем, что ![]() нормальна в
нормальна в ![]() .
.
Теорема доказана.
Следствие 2.3.2 Если в группе ![]() все
силовские подгруппы обладают супердобавлениями, то
все
силовские подгруппы обладают супердобавлениями, то ![]() дисперсивна
по Оре.
дисперсивна
по Оре.
Доказательство сразу вытекает из предыдущей леммы и определения дисперсивной по Оре группы.
Следствие 2.3.3 Если в группе ![]() все
силовские подгруппы имеют супердобавления, то
все
силовские подгруппы имеют супердобавления, то ![]() сверхразрешима.
сверхразрешима.
Доказательство. Из теоремы 2.3.1 вытекает, что группа ![]() дисперсивна по Оре. Пусть
дисперсивна по Оре. Пусть ![]() – силовская
– силовская ![]() -подгруппа для наибольшего
простого делителя
-подгруппа для наибольшего
простого делителя ![]() порядка группы
порядка группы ![]() и пусть
и пусть ![]() и
и ![]() . По условию
. По условию ![]() , где
, где ![]() – силовская
– силовская ![]() -подгруппа в
-подгруппа в ![]() ,
, ![]() – ее супердобавление. Пусть
– ее супердобавление. Пусть
![]() – силовская
– силовская ![]() -подгруппа из
-подгруппа из ![]() . Так как
. Так как ![]() – силовская
– силовская ![]() -подгруппа в
-подгруппа в ![]() , то
, то ![]() полунормальна в
полунормальна в ![]() . По лемме 2.1.6
. По лемме 2.1.6 ![]() полунормальна в
полунормальна в ![]() , то есть
, то есть ![]() , где
, где ![]() – супердобавление к
– супердобавление к ![]() в
в ![]() . По лемме 2.1.8
произведение
. По лемме 2.1.8
произведение ![]() является полунормальной в
является полунормальной в ![]() подгруппой и
подгруппой и ![]() , причем
, причем ![]() есть супердобавление к
есть супердобавление к ![]() в
в ![]() . Через
. Через ![]() шагов получим, что
шагов получим, что ![]() – полунормальная в
– полунормальная в ![]() подгруппа, где
подгруппа, где ![]() – силовская
– силовская ![]() -подгруппа для
-подгруппа для ![]() . Ясно, что
. Ясно, что ![]() и
и ![]() .
.
Пусть ![]() – подгруппа
простого порядка из
– подгруппа
простого порядка из ![]() , нормальная в
, нормальная в ![]() . Из того, что
. Из того, что ![]() полунормальна в
полунормальна в ![]() следует, что
следует, что ![]() – подгруппа группы
– подгруппа группы ![]() . Так как
. Так как ![]() , то
, то ![]() и
и ![]() . Итак, в группе
. Итак, в группе ![]() имеется нормальная
подгруппа
имеется нормальная
подгруппа ![]() простого порядка
простого порядка ![]() . По лемме 2.1.6 условие
доказываемого утверждения распространяется и на факторгруппу
. По лемме 2.1.6 условие
доказываемого утверждения распространяется и на факторгруппу ![]() . По индукции
. По индукции ![]() сверхразрешима. Теперь
сверхразрешима. Теперь ![]() сверхразрешима.
сверхразрешима.
Следствие доказано.
Следствие 2.3.4 Пусть ![]() –
группа и
–
группа и ![]() – такое множество простых
чисел, что
– такое множество простых
чисел, что ![]() для любых
для любых ![]() и
и ![]() . Если в группе
. Если в группе ![]() силовская
силовская ![]() –подгруппа обладает
супердобавлением для всех
–подгруппа обладает
супердобавлением для всех ![]() , то
, то ![]()
![]() –замкнута и ее
–замкнута и ее ![]() –холловская подгруппа
сверхразрешима.
–холловская подгруппа
сверхразрешима.
Доказательство. Пусть ![]() –
силовская
–
силовская ![]() –подгруппа для наибольшего
простого
–подгруппа для наибольшего
простого ![]() . Тогда
. Тогда ![]() – наибольший простой
делитель порядка группы
– наибольший простой
делитель порядка группы ![]() и по
теореме 2.3.1 подгруппа
и по
теореме 2.3.1 подгруппа ![]() нормальна
в
нормальна
в ![]() . По индукции
. По индукции ![]()
![]() –замкнута, поэтому
–замкнута, поэтому ![]()
![]() –замкнута и в
–замкнута и в ![]() есть
есть ![]() –холловская подгруппа
–холловская подгруппа ![]() , которая сверхразрешима по
следствию 2.2.2.
, которая сверхразрешима по
следствию 2.2.2.
Следствие доказано.
Определение 2.3.5 Конечную группу ![]() будем
называть
будем
называть ![]() –разрешимой, если
каждый из ее композиционных факторов является либо
–разрешимой, если
каждый из ее композиционных факторов является либо ![]() –группой
порядка
–группой
порядка ![]() либо
либо ![]() –группой.
–группой.
Группа ![]() разрешима в
обычном смысле тогда и только тогда, когда она
разрешима в
обычном смысле тогда и только тогда, когда она ![]() –разрешима
для всех простых
–разрешима
для всех простых ![]() Ясно, что группа
Ясно, что группа
![]()
![]() –разрешима тогда и только
тогда, когда она обладает нормальным рядом
–разрешима тогда и только
тогда, когда она обладает нормальным рядом
![]()
в котором каждая факторгруппа ![]() является
либо
является
либо ![]() –группой, либо
–группой, либо ![]() –группой. Поэтому для такой
группы можно индуктивно определить верхний
–группой. Поэтому для такой
группы можно индуктивно определить верхний ![]() –ряд.
–ряд.
![]()
где ![]() Здесь
Здесь ![]() – наибольшая нормальная
– наибольшая нормальная ![]() –подгруппа группы
–подгруппа группы ![]()
![]() – наибольшая нормальная
– наибольшая нормальная ![]() –подгруппа
–подгруппа ![]() Наименьшее натуральное
число
Наименьшее натуральное
число ![]() для которого
для которого ![]() называют
называют ![]() –длиной
–длиной ![]() группы
группы ![]()
В следующей теореме будет использован результат В.Н. Тютянова:
если для любого простого делителя ![]() порядка
группы
порядка
группы ![]() существуют бипримарные
существуют бипримарные ![]() –холловские подгруппы, то группа
–холловские подгруппы, то группа
![]() разрешима. В
доказательстве этого результата использовалась классификация конечных простых
групп.
разрешима. В
доказательстве этого результата использовалась классификация конечных простых
групп.
Теорема 2.3.6 Если в группе ![]() силовская
силовская
![]() –подгруппа обладает
супердобавлением, то
–подгруппа обладает
супердобавлением, то ![]()
![]() –разрешима и
–разрешима и ![]() для любого
для любого ![]() .
.
Доказательство. В начале приведём утверждение из работы: пусть ![]() – группа и
– группа и ![]() – её полунормальная
подгруппа. Тoгда:
– её полунормальная
подгруппа. Тoгда:
– если ![]() –
– ![]() –нильпотентна, то
нормальное замыкание
–нильпотентна, то
нормальное замыкание ![]() подгруппы
подгруппы ![]() в группе
в группе ![]() разрешимо.
разрешимо.
– если порядок ![]() подгруппы
подгруппы
![]() группы
группы ![]() нечетен, то и
нечетен, то и ![]() нечетен.
нечетен.
Рассмотрим два случая.
1) Пусть ![]() . Получаем, что
. Получаем, что ![]() нечетен, где
нечетен, где ![]() – силовская
– силовская ![]() –подгруппа группы
–подгруппа группы ![]() . Следовательно, подгруппа
. Следовательно, подгруппа ![]() разрешима. Теперь
разрешима. Теперь ![]() –
– ![]() -группа. И группа
-группа. И группа ![]()
![]() –разрешима. Пусть
–разрешима. Пусть ![]() – произвольный элемент из
– произвольный элемент из ![]() ,
, ![]() . Тогда
. Тогда ![]() из теоремы 2.3.1 и
из теоремы 2.3.1 и ![]() , где
, где ![]() – силовская
– силовская ![]() –подгруппа группы
–подгруппа группы ![]() . Следовательно, теорема
верна в этом случае.
. Следовательно, теорема
верна в этом случае.
2) Пусть ![]() . Имеем
. Имеем ![]() и
и ![]() для любой собственной
подгруппы
для любой собственной
подгруппы ![]() из
из ![]() . Из полунормальности
силовской
. Из полунормальности
силовской ![]() –подгруппы
–подгруппы ![]() группы
группы ![]() следует, что в группе
следует, что в группе ![]() существуют
существуют ![]() –
– ![]() –холловы подгруппа группы
–холловы подгруппа группы ![]() для каждого
для каждого ![]() . Таким образом, в группе
. Таким образом, в группе ![]() существуют бипримарные
существуют бипримарные ![]() –холловские подгруппы для
любого нечётного простого делителя
–холловские подгруппы для
любого нечётного простого делителя ![]() ,
поэтому группа
,
поэтому группа ![]() разрешима.
разрешима.
Теорема доказана.
Лемма 2.3.7. Пусть ![]() –
– ![]() –разрешимая группа.
–разрешимая группа.
Если ![]() – нормальная
подгруппа в
– нормальная
подгруппа в ![]() то
то ![]()
Если ![]() – подгруппа в
– подгруппа в ![]() то
то ![]()
Пусть ![]() и
и ![]() – нормальные подгруппы в
– нормальные подгруппы в ![]() тогда
тогда ![]()
Кроме того, ![]()
Пусть ![]() и
и ![]() – нормальные подгруппы в
– нормальные подгруппы в ![]() тогда
тогда ![]()
![]()
Лемма 2.3.8. Пусть ![]() –
– ![]() –разрешимая группа такая,
что
–разрешимая группа такая,
что ![]() , но
, но ![]() для всех нормальных
неединичных подгрупп
для всех нормальных
неединичных подгрупп ![]() группы
группы ![]() . Тогда справедливы
следующие условия:
. Тогда справедливы
следующие условия:
![]()
в группе ![]() существует
максимальная
существует
максимальная ![]() -нильпотентная нормальная
подгруппа
-нильпотентная нормальная
подгруппа ![]() которая является
элементарной абелевой
которая является
элементарной абелевой ![]() -группой;
-группой;
![]() –
единственная минимальная подгруппа в группе
–
единственная минимальная подгруппа в группе ![]() имеющая
добавление;
имеющая
добавление;
![]()
Лемма 2.3.9. Если ![]() –
наименьшее из чисел, принадлежащих
–
наименьшее из чисел, принадлежащих ![]() и
силовская
и
силовская ![]() –подгруппа
–подгруппа ![]() циклическая, то в группе
существует нормальная подгруппа
циклическая, то в группе
существует нормальная подгруппа ![]() такая,
что
такая,
что ![]() .
.
Непосредственно из определения ![]() –длины
получаем следующую лемму.
–длины
получаем следующую лемму.
Лемма 2.3.10 В ![]() –разрешимой
группе
–разрешимой
группе ![]() тогда и только тогда
тогда и только тогда ![]() , когда факторгруппа
, когда факторгруппа ![]()
![]() –замкнута.
–замкнута.
Лемма 2.3.11 Если в группе ![]() все
все
![]() –подгруппы имеют
супердобавления, то
–подгруппы имеют
супердобавления, то ![]() .
.
Доказательство. Из леммы 2.3.5 следует, что группа ![]()
![]() –разрешима. Применим
индукцию по порядку группы
–разрешима. Применим
индукцию по порядку группы ![]() . Тогда
по лемме 2.3.8 можно считать, что
. Тогда
по лемме 2.3.8 можно считать, что ![]() , в
группе
, в
группе ![]() подгруппа Фиттинга
подгруппа Фиттинга ![]() – минимальная нормальная
– минимальная нормальная ![]() –подгруппа. Пусть
–подгруппа. Пусть ![]() – силовская
– силовская ![]() –подгруппа группы
–подгруппа группы ![]() . По условию
. По условию ![]() полунормальна. Тогда
полунормальна. Тогда ![]() , где
, где ![]() . Для любой собственной
подгруппы
. Для любой собственной
подгруппы ![]() из
из ![]() верно, что
верно, что ![]() – подгруппа группы
– подгруппа группы ![]() . По лемме 2.1.6 все
. По лемме 2.1.6 все ![]() –подгруппы имеют
супердобавления в
–подгруппы имеют
супердобавления в ![]() . Так как
. Так как ![]() , то по индукции
, то по индукции ![]() . Заметим также, что
. Заметим также, что ![]() , поскольку
, поскольку ![]() . Теперь по лемме 2.3.10
подгруппа
. Теперь по лемме 2.3.10
подгруппа ![]() .
.
Если в подгруппе ![]() существуют
две максимальные подгруппы
существуют
две максимальные подгруппы ![]() и
и ![]() , то
, то ![]() и
и ![]() . Следовательно,
. Следовательно, ![]() и
и ![]() . Поэтому в
. Поэтому в ![]() существует единственная
максимальная подгруппа и подгруппа
существует единственная
максимальная подгруппа и подгруппа ![]() примарная
циклическая, то есть
примарная
циклическая, то есть ![]() . Если
. Если ![]() , то
, то ![]() по теореме 2.3.1. Значит
по теореме 2.3.1. Значит ![]() .
.
Пусть ![]() – подгруппа
порядка
– подгруппа
порядка ![]() из
из ![]() . Тогда
. Тогда ![]() , так как
, так как ![]() . Теперь
. Теперь ![]() , поэтому
, поэтому ![]() . Значит,
. Значит, ![]() и
и ![]() – циклическая группа
порядка, делящего
– циклическая группа
порядка, делящего ![]() . То есть
. То есть ![]() . Теперь
. Теперь ![]() .
.
Лемма доказана.
Из определения ![]() –сверхразрешимой
группы вытекают следующие две леммы.
–сверхразрешимой
группы вытекают следующие две леммы.
Лемма 2.3.12 Всякая ![]() –сверхразрешимая
группа имеет единичную
–сверхразрешимая
группа имеет единичную ![]() –длину.
–длину.
Лемма 2.3.13 Если подгруппа ![]() ,
,
![]() или
или ![]() –
– ![]() –группа и факторгруппа
–группа и факторгруппа ![]()
![]() –сверхразрешима, то и
группа
–сверхразрешима, то и
группа ![]()
![]() –сверхразрешима. В
частности, если группа
–сверхразрешима. В
частности, если группа ![]()
![]() –сверхразрешима, то и
группа
–сверхразрешима, то и
группа ![]()
![]() –сверхразрешима.
–сверхразрешима.
Теорема 2.3.14 Если в группе ![]() все
все
![]() –подгруппы имеют
супердобавления, то
–подгруппы имеют
супердобавления, то ![]()
![]() –сверхразрешима.
–сверхразрешима.
Доказательство проведём индукцией по порядку группы ![]() . В силу леммы 2.3.13 можно
считать, что
. В силу леммы 2.3.13 можно
считать, что ![]() .
.
Из леммы 2.3.9 ![]() следует,
что подгруппа
следует,
что подгруппа ![]() нормальна в
группе
нормальна в
группе ![]() . Рассмотрим подгруппу
. Рассмотрим подгруппу ![]() такую, что
такую, что ![]() . Подгруппа
. Подгруппа ![]() имеет супердобавления как
имеет супердобавления как ![]() –подгруппа, поэтому
–подгруппа, поэтому ![]() есть подгруппа группы
есть подгруппа группы ![]() . Теперь
. Теперь ![]() и
и ![]() . Следовательно, подгруппа
. Следовательно, подгруппа ![]() нормальна и в группе
нормальна и в группе ![]() . Теперь факторгруппа
. Теперь факторгруппа ![]()
![]() –сверхразрешима по
индукции. Значит и группа
–сверхразрешима по
индукции. Значит и группа ![]()
![]() –сверхразрешима.
–сверхразрешима.
Теорема доказана.
Пример 2.3.15 Если силовская ![]() -подгруппа
обладает супердобавлением, то не всегда
-подгруппа
обладает супердобавлением, то не всегда ![]() .
В симметрической группе
.
В симметрической группе ![]() силовская
силовская
![]() –подгруппа полунормальна,
но
–подгруппа полунормальна,
но ![]() .
.
Пример 2.3.16 В ![]() существует
подгруппа порядка
существует
подгруппа порядка ![]() , не имеющая
супердобавления.
, не имеющая
супердобавления.
Доказательство. Пусть ![]() , где
, где
![]()
![]()
Предположим, что подгруппа ![]() ,
имеющая порядок
,
имеющая порядок ![]() , имеет
супердобавление в
, имеет
супердобавление в ![]() . Тогда
существует подгруппа
. Тогда
существует подгруппа ![]() такая, что
такая, что ![]() и
и ![]() – собственная подгруппа
группы
– собственная подгруппа
группы ![]() для каждой подгруппы
для каждой подгруппы ![]() из
из ![]() , отличной от
, отличной от ![]() . Так как
. Так как ![]() делится на
делится на ![]() , то можно считать, что
силовская
, то можно считать, что
силовская ![]() -подгруппа
-подгруппа ![]() группы
группы ![]() содержится в
содержится в ![]() . Но теперь
. Но теперь
![]()
и ![]() , т.е.
, т.е. ![]() не является подгруппой
группы
не является подгруппой
группы ![]() , получили противоречие.
Утверждение доказано.
, получили противоречие.
Утверждение доказано.
Теперь пусть ![]() – класс
групп, у которых все подгруппы имеют супердобавления. По леммам 2.1.6 и 2.1.7
класс
– класс
групп, у которых все подгруппы имеют супердобавления. По леммам 2.1.6 и 2.1.7
класс ![]() – наследственный гомоморф.
Из предыдущего примера вытекает, что
– наследственный гомоморф.
Из предыдущего примера вытекает, что ![]() не
является радикальным классом и не является формацией. Кроме того,
не
является радикальным классом и не является формацией. Кроме того, ![]() не содержит класс вполне
факторизуемых групп.
не содержит класс вполне
факторизуемых групп.
Пример 2.3.17 Пусть ![]() –
сверхразрешимая группа Шмидта. проверим, что в
–
сверхразрешимая группа Шмидта. проверим, что в ![]() все
подгруппы обладают супердобавлениями. Действительно:
все
подгруппы обладают супердобавлениями. Действительно:
1) ![]() ;
;
2) ![]() полунормальна в
группе как подгруппа простого индекса;
полунормальна в
группе как подгруппа простого индекса;
3) если выбрать произвольную подгруппу ![]() ,
то
,
то ![]() и
и ![]() , тем более полунормальна;
, тем более полунормальна;
4) если ![]() – произвольная
непримарная подгруппа группы
– произвольная
непримарная подгруппа группы ![]() , то
, то ![]() , где
, где ![]() , и
, и ![]() .
.
Таким образом, в ![]() все
подгруппы, кроме
все
подгруппы, кроме ![]() и ей
сопряженных, нормальны, тем более имеют супердобавления.
и ей
сопряженных, нормальны, тем более имеют супердобавления.
Пример 2.3.18 Пусть ![]() –
группа диэдра порядка
–
группа диэдра порядка ![]() . Тогда
. Тогда
![]()
![]()
Проверим, что в ![]() все
подгруппы обладают супердобавлениями.
все
подгруппы обладают супердобавлениями.
Подгруппа ![]() полунормальна,
она даже нормальна.
полунормальна,
она даже нормальна.
Подгруппа ![]() полунормальна,
для неё супердобавлением является подгруппа
полунормальна,
для неё супердобавлением является подгруппа ![]() .
Так
.
Так ![]() и для единственной
собственной подгруппы
и для единственной
собственной подгруппы ![]() из
из ![]() имеем
имеем ![]() .
.
Подгруппа ![]() полунормальна,
так как
полунормальна,
так как ![]() и для любой подгруппы
всегда существует минимальное добавление в группе.
и для любой подгруппы
всегда существует минимальное добавление в группе.
Подгруппа ![]() полунормальна,
для неё супердобавлением является подгруппа
полунормальна,
для неё супердобавлением является подгруппа ![]() .
Так
.
Так ![]() и
и ![]() .
.
Подгруппа ![]() полунормальна,
для неё супердобавлением является подгруппа
полунормальна,
для неё супердобавлением является подгруппа ![]() .
Так
.
Так ![]() и
и ![]() .
.
Подгруппа ![]() полунормальна,
для неё супердобавлением является подгруппа
полунормальна,
для неё супердобавлением является подгруппа ![]() .
Так
.
Так ![]() и
и ![]() .
.
Итак, в нильпотентных группах подгруппы, обладающие супердобавлениями, могут быть ненормальными.
3. Факторизации групп дисперсивными и сверхразрешимыми подгруппами
3.1 Силовские множества и их свойства
Определение 3.1.1 Множество ![]() ,
состоящее из попарно перестановочных силовских
,
состоящее из попарно перестановочных силовских ![]() –подгрупп
из
–подгрупп
из ![]() , в точности по одной
подгруппе для каждого
, в точности по одной
подгруппе для каждого ![]() , вместе с самой
группой
, вместе с самой
группой ![]() , называется силовской
системой группы
, называется силовской
системой группы ![]() .
.
В своей книге Дерк и Хоукс использовали название «силовский базис»
вместо силовской системы ![]() . Введем
следующее определение.
. Введем
следующее определение.
Определение 3.1.2 Силовским множеством группы назовем множество силовских подгрупп, взятых по одной для каждого простого делителя порядка группы, вместе с единичной подгруппой.
Таким образом, если ![]() –
группа порядка
–
группа порядка ![]() , то множество
, то множество ![]() будет силовским
множеством. Здесь E – единичная подгруппа группы
будет силовским
множеством. Здесь E – единичная подгруппа группы ![]() ,
,
![]() – силовская
– силовская ![]() –подгруппа группы
–подгруппа группы ![]() и все числа
и все числа ![]() различны.
различны.
Из теоремы Силова следует, что каждая группа ![]() обладает силовским
множеством
обладает силовским
множеством ![]() . Если дополнительно
. Если дополнительно ![]() для всех подгрупп из
для всех подгрупп из ![]() , то силовское множество
превращается в силовскую систему, см.. Известно, что любая разрешимая группа
обладает силовской системой, и наоборот, если в группе имеется силовская
система, то группа разрешима. Кроме того, если
, то силовское множество
превращается в силовскую систему, см.. Известно, что любая разрешимая группа
обладает силовской системой, и наоборот, если в группе имеется силовская
система, то группа разрешима. Кроме того, если ![]() и
и
![]() – силовские системы
разрешимой группы
– силовские системы
разрешимой группы ![]() , то
, то ![]() для некоторого
для некоторого ![]() .
.
Пусть ![]() – некоторое
множество подгрупп группы
– некоторое
множество подгрупп группы ![]() и
и ![]() – нормальная подгруппа
группы
– нормальная подгруппа
группы ![]() . Воспользуемся следующими
обозначениями:
. Воспользуемся следующими
обозначениями:
![]()
![]()
![]()
![]()
где ![]() – некоторый
гомоморфизм группы
– некоторый
гомоморфизм группы ![]() в некоторую
группу
в некоторую
группу ![]() .
.
В разделе 3.1 изучаются свойства силовских множеств, которые необходимы при доказательстве. Для формулировок теорем потребуется следующее
Определение 3.1.3 Пусть ![]() –
некоторое множество подгрупп группы
–
некоторое множество подгрупп группы ![]() .
Подгруппа
.
Подгруппа ![]() группы
группы ![]() называется
называется ![]() –квазинормальной, если
–квазинормальной, если ![]() для всех
для всех ![]() . Если
. Если ![]() – множество всех подгрупп
группы
– множество всех подгрупп
группы ![]() , то
, то ![]() –квазинормальную подгруппу
называют квазинормальной.
–квазинормальную подгруппу
называют квазинормальной.
Лемма 3.1.4. Пусть ![]() –
силовская
–
силовская ![]() –подгруппа группы
–подгруппа группы ![]() и
и ![]() . Тогда
. Тогда ![]() – силовская
– силовская ![]() –подгруппа группы
–подгруппа группы ![]() , а
, а ![]() – силовская
– силовская ![]() –подгруппа факторгруппы
–подгруппа факторгруппы ![]() .
.
Лемма 3.1.5 Пусть ![]() –
нормальная подгруппа группы
–
нормальная подгруппа группы ![]() .
.
Если ![]() – силовское
множество группы
– силовское
множество группы ![]() , то
, то ![]() является силовским
множеством факторгруппы
является силовским
множеством факторгруппы ![]() .
.
Если ![]() – силовское
множество группы
– силовское
множество группы ![]() , то
, то ![]() является силовским
множеством подгруппы
является силовским
множеством подгруппы ![]() .
.
Если факторгруппа ![]() имеет
силовское множество
имеет
силовское множество ![]() , то найдется в
группе
, то найдется в
группе ![]() такое силовское множество
такое силовское множество ![]() , что
, что ![]() .
.
Если нормальная подгруппа ![]() группы
группы
![]() имеет силовское множество
имеет силовское множество ![]() , то найдется в группе
, то найдется в группе ![]() такое силовское множество
такое силовское множество ![]() , что
, что ![]() .
.
Если ![]() – силовское
множество группы
– силовское
множество группы ![]() и
и ![]() – некоторый гомоморфизм
группы
– некоторый гомоморфизм
группы ![]() в группу
в группу ![]() , то
, то ![]() является силовским
множеством группы
является силовским
множеством группы ![]() .
.
Доказательство. Пусть ![]() –
силовское множество группы
–
силовское множество группы ![]() .
Рассмотрим множество
.
Рассмотрим множество ![]() , в котором может
оказаться более одной единичной подгруппы, но в этом случае следует оставить
только одну единичную подгруппу. Кроме
, в котором может
оказаться более одной единичной подгруппы, но в этом случае следует оставить
только одну единичную подгруппу. Кроме ![]() множество
множество
![]() включает силовские
подгруппы факторгруппы
включает силовские
подгруппы факторгруппы ![]() по лемме 3.1.4.
Следовательно,
по лемме 3.1.4.
Следовательно, ![]() есть силовское
множество факторгруппы
есть силовское
множество факторгруппы ![]() .
.
Пусть ![]() – силовское
множество группы
– силовское
множество группы ![]() . Из равенства
. Из равенства ![]() и из того, что по
предыдущей лемме
и из того, что по
предыдущей лемме ![]() является
силовской подгруппой в группе
является
силовской подгруппой в группе ![]() получаем,
что
получаем,
что ![]() есть силовское множество в
есть силовское множество в
![]() .
.
Теперь пусть в факторгруппе ![]() известно
силовское множество
известно
силовское множество ![]() . Тогда
существуют силовские подгруппы
. Тогда
существуют силовские подгруппы ![]() такие,
что
такие,
что ![]() для
для ![]() . Рассмотрим простые числа
. Рассмотрим простые числа ![]() . Для всех таких простых
чисел существуют силовские
. Для всех таких простых
чисел существуют силовские ![]() –подгруппы
–подгруппы
![]() , где
, где ![]() . Теперь
. Теперь ![]() будет силовским множеством
группы
будет силовским множеством
группы ![]() . И выполняется равенство
. И выполняется равенство
![]()
Если ![]() – силовское
множество нормальной группы
– силовское
множество нормальной группы ![]() , то по
предыдущей лемме и по теореме Силова найдутся силовские
, то по
предыдущей лемме и по теореме Силова найдутся силовские ![]() –подгруппы
–подгруппы ![]() группы
группы ![]() , для
, для ![]() , такие, что
, такие, что ![]() . Теперь рассмотрим все
простые числа
. Теперь рассмотрим все
простые числа ![]() и для каждого
такого простого числа
и для каждого
такого простого числа ![]() в группе
в группе ![]() возьмем по одной силовской
возьмем по одной силовской
![]() –подгруппе
–подгруппе ![]() . Теперь
. Теперь ![]() будет силовским множеством
группы
будет силовским множеством
группы ![]() и
и ![]() .
.
Рассмотрим ![]() –
силовское множество группы
–
силовское множество группы ![]() и
гомоморфизм
и
гомоморфизм ![]() группы
группы ![]() в группу
в группу ![]() . По принятому обозначению
. По принятому обозначению ![]() . По свойствам гомоморфизма
подгруппа
. По свойствам гомоморфизма
подгруппа ![]() будет силовской подгруппой
группы
будет силовской подгруппой
группы ![]() . То есть
. То есть ![]() есть силовское множество
группы
есть силовское множество
группы ![]() .
.
Лемма доказана.
Лемма 3.1.6 Пусть ![]() –
силовское множество группы
–
силовское множество группы ![]() и
и ![]() –
– ![]() –квазинормальная подгруппа
группы
–квазинормальная подгруппа
группы ![]() . Тогда верны следующие
утверждения:
. Тогда верны следующие
утверждения:
если ![]() – гомоморфизм
группы
– гомоморфизм
группы ![]() , тогда подгруппа
, тогда подгруппа ![]()
![]() –квазинормальна в группе
–квазинормальна в группе ![]() ;
;
если ![]() и
и ![]() – нормальная подгруппа
группы
– нормальная подгруппа
группы ![]() , то подгруппа
, то подгруппа ![]()
![]() –квазинормальна в группе
–квазинормальна в группе ![]() ;
;
если ![]() – произвольная
нормальная подгруппа группы
– произвольная
нормальная подгруппа группы ![]() , то в
факторгруппе
, то в
факторгруппе ![]() подгруппа
подгруппа ![]() будет
будет ![]() –квазинормальной.
–квазинормальной.
Доказательство. По лемме 3.1.5 множество ![]() является силовским
множеством группы
является силовским
множеством группы ![]() . Так как
. Так как ![]() для
для ![]() , то имеем
, то имеем ![]() и
и ![]() есть
есть ![]() -квазинормальная подгруппа
в
-квазинормальная подгруппа
в ![]() .
.
По лемме 3.1.5 множество ![]() будет
силовским множеством группы
будет
силовским множеством группы ![]() . Так
как
. Так
как ![]() – подгруппа группы
– подгруппа группы ![]() , то
, то ![]() – подгруппа группы
– подгруппа группы ![]() . Поэтому
. Поэтому ![]() .
.
По лемме 3.1.5 множество ![]() будет
силовским множеством факторгруппы
будет
силовским множеством факторгруппы ![]() . И на
основании равенства
. И на
основании равенства ![]() получаем
перестановочность подгруппы
получаем
перестановочность подгруппы ![]() с
подгруппами силовского множества
с
подгруппами силовского множества ![]() факторгруппы
факторгруппы
![]() .
.
Лемма доказана.
Лемма 3.1.7 Пусть группа ![]() с
силовским множеством
с
силовским множеством ![]() ,
, ![]() – подгруппа группы
– подгруппа группы ![]() . Если подгруппа
. Если подгруппа ![]()
![]() –квазинормальна, то сама
подгруппа
–квазинормальна, то сама
подгруппа ![]() будет
будет ![]() –квазинормальной для любого
элемента
–квазинормальной для любого
элемента ![]() группы
группы ![]() .
.
Доказательство. По условию ![]() ,
для любой подгруппы
,
для любой подгруппы ![]() , произвольного
элемента
, произвольного
элемента ![]() . Рассмотрим произведение
. Рассмотрим произведение
![]()
Так как ![]() – подгруппа
группы
– подгруппа
группы ![]() , то
, то ![]() – подгруппа, поэтому
– подгруппа, поэтому ![]() , то есть
, то есть ![]() –
– ![]() –квазинормальная подгруппа
группы
–квазинормальная подгруппа
группы ![]() .
.
Лемма доказана.
Пусть ![]() – силовское
множество группы
– силовское
множество группы ![]() . Выше
пересечение
. Выше
пересечение ![]() определялось для
нормальной подгруппы
определялось для
нормальной подгруппы ![]() группы
группы ![]() . В этом случае по лемме
3.1.5 пересечение является силовским множеством группы
. В этом случае по лемме
3.1.5 пересечение является силовским множеством группы ![]() . Если
. Если ![]() – произвольная, не
обязательно нормальная, подгруппа группы
– произвольная, не
обязательно нормальная, подгруппа группы ![]() ,
то положим
,
то положим ![]() . Отметим, что в этом
случае
. Отметим, что в этом
случае ![]() может не быть силовским
множеством группы
может не быть силовским
множеством группы ![]() .
.
Лемма 3.1.8 Пусть ![]() –
группа,
–
группа, ![]() – ее силовское множество.
Если
– ее силовское множество.
Если ![]() –
– ![]() –квазинормальная подгруппа
группы
–квазинормальная подгруппа
группы ![]() , причем
, причем ![]() и индекс
и индекс ![]() в группе
в группе ![]() примарный, то
примарный, то ![]() – примарная группа.
– примарная группа.
Доказательство. Пусть ![]() и
пусть
и
пусть ![]() . Так как
. Так как ![]() –
– ![]() –квазинормальная подгруппа,
то
–квазинормальная подгруппа,
то ![]() – подгруппа группы
– подгруппа группы ![]() для каждого
для каждого ![]() . По теореме об индексах
. По теореме об индексах
![]()
где ![]() ,
, ![]() . Для каждого
. Для каждого ![]() имеем
имеем ![]() , то есть
, то есть ![]() и
и ![]() . Но по условию
. Но по условию ![]() , поэтому
, поэтому ![]() и
и ![]() –
– ![]() –группа.
–группа.
Лемма доказана.
Лемма 3.1.9 Пусть ![]() –
нормальная подгруппа группы
–
нормальная подгруппа группы ![]() . Если
. Если ![]() – циклическая
– циклическая ![]() –подгруппа факторгруппы
–подгруппа факторгруппы ![]() , то существует элемент
, то существует элемент ![]() такой, что
такой, что ![]() –
– ![]() –подгруппа и
–подгруппа и ![]() .
.
Доказательство. Пусть ![]() –
минимальное добавление к подгруппе
–
минимальное добавление к подгруппе ![]() в
группе
в
группе ![]() . Тогда
. Тогда ![]() по лемме 2.3.23, поэтому
по лемме 2.3.23, поэтому ![]() является
является ![]() -группой. Так как
-группой. Так как ![]() и
и ![]() циклическая, тогда
циклическая, тогда ![]() – циклическая подгруппа,
то есть
– циклическая подгруппа,
то есть ![]() подгруппа из
подгруппа из ![]() для некоторого
для некоторого ![]() .
.
Лемма доказана.
3.2 Дисперсивность и сверхразрешимость факторизуемых групп
Будем использовать запись ![]() для
обозначения некоторого силовского множества группы
для
обозначения некоторого силовского множества группы ![]() .
.
Теорема 3.2.1 Пусть группа ![]() ,
где подгруппы
,
где подгруппы ![]() и
и ![]() дисперсивны по Оре. И
пусть
дисперсивны по Оре. И
пусть ![]() и
и ![]() – силовские множества
подгрупп
– силовские множества
подгрупп ![]() и
и ![]() . Если циклические
примарные подгруппы из
. Если циклические
примарные подгруппы из ![]()
![]() –квазинормальны, а
циклические примарные подгруппы из
–квазинормальны, а
циклические примарные подгруппы из ![]()
![]() –квазинормальны, то группа
–квазинормальны, то группа ![]() дисперсивна по Оре.
дисперсивна по Оре.
Доказательство. Предположим, что теорема неверна. Тогда существуют
группы, удовлетворяющие условию теоремы и не удовлетворяющие ее заключению.
Пусть ![]() – не дисперсивная по Оре
группа наименьшего порядка, для которой все условия теоремы выполняются. Тогда
для любой неединичной нормальной подгруппы
– не дисперсивная по Оре
группа наименьшего порядка, для которой все условия теоремы выполняются. Тогда
для любой неединичной нормальной подгруппы ![]() факторгруппа
факторгруппа
![]() является произведением
своих подгрупп
является произведением
своих подгрупп ![]() и
и ![]() . Так как
. Так как ![]() и
и ![]() , то подгруппы
, то подгруппы ![]() и
и ![]() дисперсивны по Оре.
Рассмотрим их силовские множества. Ввиду леммы 2.1.5 силовские множества
подгрупп
дисперсивны по Оре.
Рассмотрим их силовские множества. Ввиду леммы 2.1.5 силовские множества
подгрупп ![]() и
и ![]() соответственно равны
множествам
соответственно равны
множествам ![]() и
и ![]() .
.
Пусть ![]() – произвольная
циклическая примарная подгруппа факторгруппы
– произвольная
циклическая примарная подгруппа факторгруппы ![]() .
Рассмотрим произведение циклической подгруппы
.
Рассмотрим произведение циклической подгруппы ![]() и
произвольной силовской подгруппы
и
произвольной силовской подгруппы ![]() . Ввиду
леммы 3.1.9 существует примарный элемент
. Ввиду
леммы 3.1.9 существует примарный элемент ![]() такой,
что
такой,
что ![]() . Поэтому
. Поэтому
![]()
![]()
Аналогично проверяется перестановочность циклических примарных
подгрупп из ![]() с элементами силовского
множества
с элементами силовского
множества ![]() . Таким образом, для
факторгруппы
. Таким образом, для
факторгруппы ![]() все условия леммы
выполняются, а так как порядок факторгруппы
все условия леммы
выполняются, а так как порядок факторгруппы ![]() меньше
порядка группы
меньше
порядка группы ![]() , то по индукции
факторгруппа
, то по индукции
факторгруппа ![]() будет дисперсивна по Оре.
будет дисперсивна по Оре.
Пусть теперь ![]() –
наибольший простой делитель порядка группы
–
наибольший простой делитель порядка группы ![]() и
и
![]() – силовская
– силовская ![]() -подгруппа подгруппы
-подгруппа подгруппы ![]() . Так как
. Так как ![]() дисперсивна по Оре, то
подгруппа
дисперсивна по Оре, то
подгруппа ![]() нормальна в
нормальна в ![]() и
и ![]() . Если
. Если ![]() – некоторый примарный
– некоторый примарный ![]() -элемент из
-элемент из ![]() , то
, то ![]() по условию леммы. Теперь
по условию леммы. Теперь ![]() нормальная подгруппа в
нормальная подгруппа в ![]() и
и ![]() -холловская подгруппа
-холловская подгруппа ![]() из
из ![]() содержится в
содержится в ![]() . Поэтому
. Поэтому ![]() . Аналогично,
. Аналогично, ![]() , поэтому силовская
, поэтому силовская ![]() -подгруппа
-подгруппа ![]() группы
группы ![]() нормальна в группе
нормальна в группе ![]() . По индукции факторгруппа
. По индукции факторгруппа ![]() дисперсивна по Оре, а так
как
дисперсивна по Оре, а так
как ![]() – наибольший простой
делитель порядка группы
– наибольший простой
делитель порядка группы ![]() , то
группа
, то
группа ![]() дисперсивна по Оре.
дисперсивна по Оре.
Теорема доказана.
Пусть ![]() и
и ![]() – подгруппы группы
– подгруппы группы ![]() . Будем говорить, что
. Будем говорить, что ![]() квазинормальна в
квазинормальна в ![]() , если
, если ![]() перестановочна с каждой
подгруппой из
перестановочна с каждой
подгруппой из ![]() . Тогда можно
сформулировать следующий результат, вытекающий из леммы 3.2.1.
. Тогда можно
сформулировать следующий результат, вытекающий из леммы 3.2.1.
Следствие 3.2.2. Пусть ![]() и
и
![]() – дисперсивные по Оре
подгруппы группы
– дисперсивные по Оре
подгруппы группы ![]() такие, что
такие, что ![]() . И пусть
. И пусть ![]() квазинормальна в
квазинормальна в ![]() и
и ![]() квазинормальна в
квазинормальна в ![]() . Тогда группа
. Тогда группа ![]() дисперсивна по Оре.
дисперсивна по Оре.
Теорема 3.2.3 Пусть ![]() ,
, ![]() – сверхразрешимые
подгруппы группы
– сверхразрешимые
подгруппы группы ![]() . И пусть
. И пусть ![]() и
и ![]() – силовские системы
подгрупп
– силовские системы
подгрупп ![]() и
и ![]() , и
, и ![]() . Если циклические
примарные подгруппы из
. Если циклические
примарные подгруппы из ![]()
![]() –квазинормальны и
циклические примарные подгруппы из
–квазинормальны и
циклические примарные подгруппы из ![]()
![]() –квазинормальны, то группа
–квазинормальны, то группа ![]() сверхразрешима.
сверхразрешима.
Доказательство. Допустим, что теорема неверна. Тогда существует
несверхразрешимая группа ![]() наименьшего
порядка, для которой все условия теоремы верны.
наименьшего
порядка, для которой все условия теоремы верны.
Проверим, что если ![]() –
силовская система группы
–
силовская система группы ![]() , то
, то ![]() – силовская система
факторгруппы
– силовская система
факторгруппы ![]() . Пусть
. Пусть ![]() – силовская система группы
– силовская система группы
![]() и
и ![]() – нормальная подгруппа
группы
– нормальная подгруппа
группы ![]() . Отметим, что по
определению силовской системы
. Отметим, что по
определению силовской системы ![]() для
всех подгрупп из
для
всех подгрупп из ![]() . Тогда в
факторгруппе
. Тогда в
факторгруппе ![]() рассмотрим множество
подгрупп
рассмотрим множество
подгрупп ![]() . По лемме 3.1.4
. По лемме 3.1.4 ![]() является силовской
подгруппой факторгруппы
является силовской
подгруппой факторгруппы ![]() .
Возьмём две произвольные подгруппы
.
Возьмём две произвольные подгруппы ![]() и
и ![]() из множества
из множества ![]() . Рассмотрим их
произведение
. Рассмотрим их
произведение
![]()
Таким образом, по определению 3.1.1 мы получаем, что ![]() является силовской
системой факторгруппы
является силовской
системой факторгруппы ![]() .
.
Теперь легко проверить, что условия теоремы наследуются всеми факторгруппами
группы ![]() . По индукции все
нетривиальные факторгруппы группы
. По индукции все
нетривиальные факторгруппы группы ![]() сверхразрешимы.
Если подгруппа Фраттини
сверхразрешимы.
Если подгруппа Фраттини ![]() , то все
условия теоремы переносятся на факторгруппу
, то все
условия теоремы переносятся на факторгруппу ![]() .
И по индукции получаем сверхразрешимость факторгруппы
.
И по индукции получаем сверхразрешимость факторгруппы ![]() . Откуда вытекает
сверхразрешимость и самой группы
. Откуда вытекает
сверхразрешимость и самой группы ![]() .
Поэтому подгруппа Фраттини группы
.
Поэтому подгруппа Фраттини группы ![]() единична.
Если в группе
единична.
Если в группе ![]() найдутся две
минимальные нормальные подгруппы
найдутся две
минимальные нормальные подгруппы ![]() и
и ![]() , то в силу индуктивных
рассуждений факторгруппы
, то в силу индуктивных
рассуждений факторгруппы ![]() и
и ![]() будут сверхразрешимы.
Поэтому
будут сверхразрешимы.
Поэтому ![]() будет также
сверхразрешима, то есть сверхразрешима группа
будет также
сверхразрешима, то есть сверхразрешима группа ![]() .
Значит в группе
.
Значит в группе ![]() существует не
более одной минимальной нормальной подгруппы, а подгруппа Фиттинга является
единственной минимальной нормальной подгруппой. Ввиду предыдущей теоремы группа
существует не
более одной минимальной нормальной подгруппы, а подгруппа Фиттинга является
единственной минимальной нормальной подгруппой. Ввиду предыдущей теоремы группа
![]() дисперсивна по Оре, значит
для наибольшего простого делителя
дисперсивна по Оре, значит
для наибольшего простого делителя ![]() порядка
группы
порядка
группы ![]() силовская
силовская ![]() –подгруппа
–подгруппа ![]() из
из ![]() является минимальной
нормальной подгруппой. Допустим, что
является минимальной
нормальной подгруппой. Допустим, что ![]() делит
порядок подгруппы
делит
порядок подгруппы ![]() . Так как
. Так как ![]() сверхразрешима, то в
сверхразрешима, то в ![]() имеется нормальная
подгруппа
имеется нормальная
подгруппа ![]() простого порядка
простого порядка ![]() . По условию теоремы
произведение
. По условию теоремы
произведение ![]() есть подгруппа группы
есть подгруппа группы ![]() , где
, где ![]() –
– ![]() –холлова подгруппа группы
–холлова подгруппа группы ![]() , являющаяся произведением
всех силовских
, являющаяся произведением
всех силовских ![]() –подгрупп из
силовской системы
–подгрупп из
силовской системы ![]() . Поэтому
. Поэтому ![]() – нормальная подгруппа
группы
– нормальная подгруппа
группы ![]() , поскольку все подгруппы
, поскольку все подгруппы ![]() -замкнутой группы
-замкнутой группы ![]() являются
являются ![]() –замкнутыми. Теперь
–замкнутыми. Теперь ![]() , поэтому
, поэтому ![]() нормальна в
нормальна в ![]() и по индукции
и по индукции ![]() сверхразрешима. Значит и
сверхразрешима. Значит и ![]() сверхразрешима.
сверхразрешима.
Теорема доказана.
Данная теорема является обобщением следующих результатов.
Следствие 3.2.4. Пусть ![]() и
и
![]() – сверхразрешимые
подгруппы группы
– сверхразрешимые
подгруппы группы ![]() такие, что
такие, что ![]() . И пусть
. И пусть ![]() квазинормальна в
квазинормальна в ![]() и
и ![]() квазинормальна в
квазинормальна в ![]() . Тогда
. Тогда ![]() сверхразрешима.
сверхразрешима.
Следствие 3.2.5. Пусть группа ![]() ,
где
,
где ![]() ,
, ![]() – сверхразрешимые
подгруппы группы
– сверхразрешимые
подгруппы группы ![]() взаимно простых
порядков с силовскими системами
взаимно простых
порядков с силовскими системами ![]() и
и ![]() соответственно. Если
соответственно. Если ![]() и циклические подгруппы из
и циклические подгруппы из
![]()
![]() –квазинормальны,
–квазинормальны, ![]() и циклические подгруппы из
и циклические подгруппы из
![]()
![]() –квазинормальны, то группа
–квазинормальны, то группа ![]() сверхразрешима.
сверхразрешима.
Следствие 3.2.6. Пусть группа ![]() ,
где
,
где ![]() ,
, ![]() – сверхразрешимые
подгруппы группы
– сверхразрешимые
подгруппы группы ![]() с силовскими
системами
с силовскими
системами ![]() и
и ![]() соответственно. Если
элементы силовских систем
соответственно. Если
элементы силовских систем ![]() и
и ![]() попарно перестановочны,
циклические подгруппы из
попарно перестановочны,
циклические подгруппы из ![]()
![]() –квазинормальны,
циклические подгруппы из
–квазинормальны,
циклические подгруппы из ![]()
![]() –квазинормальны, то группа
–квазинормальны, то группа ![]() сверхразрешима.
сверхразрешима.
Заключение
В дипломной работе рассмотрены группы с ограничениями на минимальные добавления к выделенным подгруппам. Изучены следующие вопросы:
– критерий существования супердобавления к максимальной подгруппе,
на основе которого устанавливаются новые признаки сверхразрешимости как самой
группы, так и отдельных её подгрупп; в частности доказано, что максимальная
подгруппа ![]() группы
группы ![]() обладает супердобавлением
в группе
обладает супердобавлением
в группе ![]() тогда и только тогда,
когда индекс
тогда и только тогда,
когда индекс ![]() в
в ![]() есть простое число;
есть простое число;
– изучено строение группы, у которой силовские подгруппы обладают
супердобавлениями; а именно пусть ![]() –
наибольший простой делитель порядка группы
–
наибольший простой делитель порядка группы ![]() и
и
![]() – ее силовская
– ее силовская ![]() -подгруппа. Если
-подгруппа. Если ![]() обладает супердобавлением
в
обладает супердобавлением
в ![]() , то
, то ![]() – нормальная подгруппа
группы
– нормальная подгруппа
группы ![]() ;
;
– с помощью введенного понятия силовского множества изучены новые признаки дисперсивности и сверхразрешимости факторизуемых групп с перестановочными циклическими подгруппами из факторов:
пусть группа ![]() , где
подгруппы
, где
подгруппы ![]() и
и ![]() дисперсивны по Оре. И
пусть
дисперсивны по Оре. И
пусть ![]() и
и ![]() – силовские множества
подгрупп
– силовские множества
подгрупп ![]() и
и ![]() . Если циклические
примарные подгруппы из
. Если циклические
примарные подгруппы из ![]()
![]() –квазинормальны, а
циклические примарные подгруппы из
–квазинормальны, а
циклические примарные подгруппы из ![]()
![]() –квазинормальны, то группа
–квазинормальны, то группа ![]() дисперсивна по Оре.
дисперсивна по Оре.
Список использованных источников
1 Васильев А.Ф. и Васильева Т.И. О конечных группах, у которых главные факторы являются простыми группами // Известия ВУЗов. Серия «Математика». – 1997. – N11. – 10–14 с.
2 Курносенко Н.М. О факторизации конечных групп сверхразрешимыми и нильпотентными подгруппами // Вопросы алгебры. Гомель: Изд-во ГГУ им. Ф. Скорины. Вып. 12. – 1998. – 113–122 с.
3 Монахов В.С. Введение в теорию конечных групп и их классов // Гомель: Гомельский государственный университет им. Ф. Скорины, 2003. – 320 с.
4 Подгоргная В.В. Минимальные добавления к подгруппам конечных групп. Курс лекций // Гомель: Гомельский государственный университет им. Ф. Скорины, 2003. – 65 с.
5 Подгорная В.В. Факторизации конечных групп дисперсивными и сверхроазрешимыми подгруппами // Веснiк Вiцебскага дзяржаунага Унiверсiтэта. – Витебск: ВГУ, 1999. – №4. – С. 80–82.
6 Подгорная В.В. Полунормальные подгруппы и сверхразрешимость конечных групп // Весцi НАН Беларусi. Сер. фiз.–матэм. навук. – Мiнск, 2000. – №4. – 22–25 с.
7 Тютянов В.Н. К гипотезе Холла // Гомель, 2001. – №6. – 5 с. –
8 Черников С.Н. Группы с заданными свойствами системы подгрупп // М.: Наука, 1980. – 384 c.
9 Шеметков Л.А. Факторизации конечных групп // ДАН СССР. – 1968. – 178, №3. – С. 559–562.
10 Шеметков Л.А. Формации конечных групп // М.: Наука, 1978. – 272 c.
11 Assad M., Shaalan, On the supersolvability of finite groups // Arch. Math. – 1989. – 53. – 318–326 p.
12 Baer R. Classes of finite groups and their properties // Illinois J. Math. – 1957. – V.I. – 115–187 p.
13 Doerk K., Hawkes T. Finite soluble groups // Walter de Gruyter, Berlin – New York, 1992. – 889 p.
14 Friesen D.K. Products of normal supersolvable subgroups // Proc. Amer. Math. Soc. – 1971. – 30, №1. – 46–48 p.
15 Hall P. A characteristic property of soluble groups // J. London Math. Soc. – 1937. – 12. – P. 198–200.
16 Huppert В. Endliche gruppen, I // Berlin; Heidelberg; New York: Springer, 1967. – 793 p.
17 Carocca A., Matos H. Some solvability criteria for finite groups // Hokkaido Mathematical Joyrnal. – 1997. – Vol.26. – 157–161 p.