Дипломная работа: Полуполя, являющиеся простыми расширениями с помощью комплексного числа
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ
Математический факультет
Кафедра алгебры и геометрии
Выпускная квалификационная работа
Полуполя, являющиеся простыми расширениями с помощью комплексного числа
Выполнил
студент 5 курса
математического факультета
Чупраков Дмитрий Вячеславович
_____________________/подпись/
Научный руководитель:
д.ф-м.н., профессор Е.М. Вечтомов
_____________________/подпись/
Рецензент:
к.ф-м.н., доцент В.В. Чермных
_____________________/подпись/
Допущена к защите в ГАК
Зав. кафедрой ______________________д.ф-м.н., профессор Е.М. Вечтомов
(подпись) “__” _________
Декан факультета _____________________к.ф-м.н., доцент В.И. Варанкина
(подпись) “__” _________
Киров
2005
Содержание
Содержание. 2
Введение. 3
Глава 1. 5
1.1. Базовые понятия и факты.. 5
1.2. Простое расширение Q+(a) 5
1.3. Минимальное соотношение алгебраического элемента над полуполем рациональных неотрицательных чисел. 7
Глава 2. Однопорожденные полуполя. 9
2.1. Структура простого расширения полуполя неотрицательных рациональных чисел 9
2.2. Расширения полуполя неотрицательных действительных чисел комплексным числом. 11
2.3. Расширения полуполя неотрицательных рациональных чисел комплексным числом 12
2.4. Примеры.. 20
Литература. 22
Введение
Теория полуполей – одно из интенсивно развивающихся разделов общей алгебры, являющейся обобщением теории полей. Одним из основных способов исследования полей является построение их расширений. Поэтому естественно исследовать расширения полуполей. Эта проблема освещена в статье А.В.Ряттель [3] и диссертации И.И.Богданова. Но в них рассматриваются случаи упорядочиваемых расширений. Интересно рассмотреть неупорядочиваемые расширения. Этому вопросу посвящена данная квалификационная работа
Целью квалификационной работы является исследование однопорожденных расширений полуполей неотрицательных рациональных чисел и неотрицателных действительных чисел комплексным числом на предмет выявления признаков и свойств, позволяющих упростить поиск расширений, являющихся полуполями.
Выпускная квалификационная работа состоит из двух глав. В главе 1 представлены предварительные сведения, необходимые для изучения однопорожденных расширений полуполей. Глава 2 посвящена исследованию однопорожденных расширений полуполей.
В работе принята сквозная тройная нумерация теорем и лемм, где первое число – номер главы, второе – номер параграфа, третье – номер в параграфе. Например, теорема 2.1.1 – первая теорема первого параграфа второй главы.
Основными результатами работы являются:
·
Теорема 2.2.1. Любое расширение 
, где 
, является полем С.
·
Теорема 2.3.1. Если 
, то 
–
поле тогда и только тогда, когда Q+(-a2) – поле, позволяющая выявлять полуполя вида 
.
·
Теорема 2.3.6.
Если минимальный
многочлен f-g порождает полуполе то, он либо имеет
положительный действительный корень, либо корень 
,
такой что 
и последовательность (**),
заданная числами p и q, не
содержит отрицательных элементов.
Последовательность 
задается следующим образом:
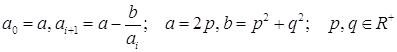
Эта теорема помогает сократить область поиска расширений, являющихся полуполями.
·
Теорема 2.3.7. Для комплексных чисел 
расширение 
, минимальное
соотношение которого имеет положительный корень, является полуполем.
Глава 1.
1.1. Базовые понятия и факты
Определение: Алгебра <P, +, ×> называется полуполем, если
(1) <Р, +> – коммутативная полугруппа с 0;
(2) <Р, ×> – группа с 1;
(3) Дистрибутивность
a. 
b. 
(4)
Не сложно показать, что Q+ является полуполем.
Определение: Пусть Р – подполуполе
полуполя F, 
,
тогда простым расширением полуполя P с помощью элемента a называется наименьшее подполуполе полуполя F, содержащее множество P и элемент a.
Простое расширение P с
помощью a обозначается P(a).
1.2. Простое расширение Q+(a)
Теорема 1.2.1. Произвольное полутело либо аддитивно идемпотентно, либо содержит копию Q+ в качестве полутела.
Доказательство. Предположим, что S – неидемпотентное полутело, т.е. найдется такой ненулевой элемент sÎS, что s+s¹s. Откуда
.
Рассмотрим суммы единиц.
Через 
обозначим сумму k единиц (при kÎN). Так как любое полутело является
антикольцом, то 
. Покажем, что
суммы различного числа единиц в S различны.
Допустим от противного, что 
при
некоторых натуральных m<n. Положим l=n-mÎN. Тогда 
.
Прибавляя к обеим частям этого равенства элемент 
,
получим
.
Применяя эту процедуру несколько раз, будем иметь
для любого tÎN.
По свойству Архимеда, найдется
такое tÎN, что tl>n. При k=tl имеем 
и n<k. Тогда
.
Откуда 1=1+1 (
). Получили противоречие.
Следовательно, полутело S содержит аддитивную копию N. Но тогда S содержит и частные сумм 1, т.е. содержит копию полуполя Q+, причем, очевидно, операции в Q+ и S согласованы.
■
Теорема 1.2.2.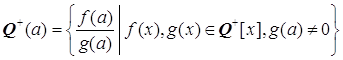 
- простое расширение
полуполя Q+.
Доказательство. Заметим, что Q+(a)
– полуполе. Кроме того, а Î Q+(a). Это не сложно увидеть, взяв 
. Очевидно 
.
Предположим, что есть полуполе P меньшее Q+(a),
содержащее а и Q+.
Тогда оно содержит все выражения вида 
.
Так как P – полуполе, то 
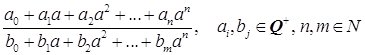. Таким образом, 
. Так как P – минимальное полуполе, то 
. То есть, 
–простое расширение
полуполя Q+.
■
Аналогично доказывается следующее утверждение.
Теорема 1.2.3. 
- простое расширение поля Q.
1.3. Минимальное соотношение алгебраического элемента над полуполем рациональных неотрицательных чисел
Пусть а –
алгебраическое число. Тогда минимальный многочлен F числа а имеет
степень ≥ 1. Тогда обозначим через f многочлен, составленный из положительных одночленов многочлена
F, а многочлен g составим из
отрицательных членов, взятых с противоположными знаками. Тогда 
. 
, тогда 
.
Покажем, что любое
равенство 
получается из , где 
. Заметим, что 
, так как а – корень
, а – минимальный многочлен
для a. Представим 
, где 
составлен из положительных
одночленов многочлена h,
а 
‑ составлен
из отрицательных одночленов многочлена h, взятых с противоположным знаком. Таким образом,
Приведем подобные члены в
паре , и найдем такой 
, что
, 
не имеют подобных членов.
Аналогично найдем 
, что
и
не имеют подобных членов.
Получаем
Так как 
не имеют подобных членов и
не имеют подобных членов,
то
, 
или
, 
.
Найдем значения этих многочленов в точке а.
,
.
Итак,
,
.
То есть, 
тогда и только тогда,
когда 
.
Будем говорить, что Q+(a)
порождается минимальным соотношением .
Глава 2. Однопорожденные полуполя
2.1. Структура простого расширения полуполя неотрицательных рациональных чисел
Для простого расширения справедливы следующие
теоремы.
Теорема 2.1.1. Пусть простое
расширение 
, a – алгебраический элемент над . Тогда эквивалентны
следующие утверждения:
(1) – поле;
(2) 
;
(3) 
;
(4) 
;
(5) 
.
Доказательство.
·
(1)®(2): Пусть – поле. Так как 
- простое расширение поля Q элементом a. То 
.
Однако, 
. Таким образом, .
· (2)®(3): Заметим, что достаточно показать, что
.
Пусть его нет, тогда
покажем, что никакой ненулевой элемент 
не
будет обратим. Рассмотрим
и
,
тогда
.
По предположению, этот
многочлен – тождественный ноль. А значит. 
.
Так как 
, то 
. То есть, оба многочлена –
нулевые. Мы же брали ненулевой многочлен b. Это показывает справедливость (3).
·
(3)®(4): Пусть , тогда 
. Так как (f – g)(a) = 0, то h(a) = 0.
·
(4)®(5): Пусть , покажем, что 
.
Так как h(a)=0, то 
.
Покажем, что . Рассмотрим
.
Если b0≠0, то
.
Если h0=0, то
.
Так как a≠0, то
.
Тогда
.
Итак, .
·
(5)®(1): Пусть , покажем, что Q+(a)
– поле. Действительно, мы знаем, что Q+(a)
– полуполе. Рассмотрим bÎQ+(a), тогда 
.
b + (‑b)=0. То есть, Q+(a)
– поле.
Итак, мы показали, что все утверждения равносильны. ■
Доказанный факт влечет следующую теорему.
Теорема 2.1.2. Пусть Q+(a) простое расширение Q+, a – алгебраический элемент над Q+. Тогда эквивалентны следующие утверждения:
(1) Q+(a) –полуполе;
(2) 
;
(3) 
;
(4) 
;
(5) 
.
Доказательство. Несложно установить равносильность утверждений (1) ‑ (4), исходя из предыдущей теоремы. Докажем условие равносильность их утверждению (5).
Из условия (5) следует, что никакой элемент не обратим по сложению. Тогда Q+(a) не является полем, а значит Q+(a) – полуполе. Докажем, что из (3) следует (5). Действительно, согласно условию (3),
("hÎQ+[a], h≠0) h(a)≠0.
То есть, если h(a)=0, то h=0. Пусть h(a)=(x+y)(a)=0. Тогда
.
Тогда (xi+yi)=0.
Так как xiÎQ+ и yiÎQ+, то xi=yi=0. А значит, x=y=0.
Теорема доказана.
■
2.2. Расширения полуполя неотрицательных действительных чисел комплексным числом
Теорема 2.2.1. Любое расширение ,
где , является полем С.
Доказательство. Пусть 
,
и при a > 0. Тогда находится
строго в первой или четвертой четверти комплексной плоскости.
Очевидно, существует натуральное n, что 
лежит
строго во второй или третьей четверти. То есть, 
,
где c < 0, 
.
Значит,
и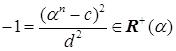 
. По теореме 2.1.1, – поле. Очевидно, что 
. То есть, является полем С.
Аналогично рассматривается случай 
■
2.3. Расширения полуполя неотрицательных рациональных чисел комплексным числом
Теорема 2.3.1. Если , то –
поле тогда и только тогда, когда Q+(-a2) – поле.
Доказательство. По теореме 2.1.1 Q+(ai) – поле равносильно существованию
f¹0, f(ai)=0.
Так как все степени aiÎQ+(ai). Рассмотрим некоторый многочлен
.
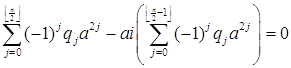Равенство выполняется тогда и только тогда, когда действительная и мнимая часть равны нулю.
То есть,
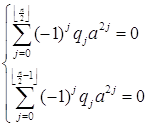
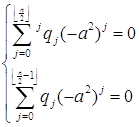
Это верно тогда и только тогда, когда Q+(-a2) – поле.
Получили, что Q+(ai) – поле тогда и только тогда, когда Q+(-a2) – поле. ■
Как следствие получаем более ценные утверждения.
Следствие 1. Если , то Q+(ai) – полуполе тогда и только тогда,
когда Q+(-a2) –
полуполе.
Следствие 2. Если 
и Q+(-b2) – полуполе, aÎQ+(-b2), то Q+(a + bi) – полуполе.
Теорема 2.3.2. Пусть –
комплексный корень квадратного трехчлена f(x) неприводимого над Q. Тогда 
– полуполе в том и только
том случае, когда f(x) имеет положительный действительный корень.
Доказательство. Пусть удовлетворяет
минимальному соотношению, являющемуся квадратным уравнением без положительных
корней. Тогда 
, где D – дискриминант минимального
соотношения.
Рассмотрим минимальный
многочлен, соответствующий данному минимальному значению. Он имеет вид 
. Если b, c ≥ 0, то имеем многочлен из
. Пусть многочлен имеет два
отрицательных корня, тогда 
, 
. То есть 
. Если многочлен не имеет
действительных корней, 
то
(*)
То есть, 
.
Рассмотрим 
.
При 
получаем
многочлен из Q+[x]. Пусть 
. Введем
обозначения:
, 
,
,
, 
,
.
Тогда многочлен примет
вид 
. Умножим его на 
, получим многочлен 
. Если 
, то это искомый многочлен
иначе умножим его на 
.
Докажем, что, проделав
такую операцию достаточно большое количество раз, мы получим многочлен из Q+. Докажем, что найдется такие k, что 
.
При этом 
. Для начала найдем
дискриминант уравнения 
.
То есть, дискриминант Dl+1 имеет тот же знак, что и Dl. Так как D0<0, то пользуясь методом математической индукции заключаем, что любой дискриминант Dl<0.
Рассмотрим неравенство , подставим 
, 
. Получим
.
То есть,
.
Зная, что 
заметим
.
Итак, для доказательства нам достаточно установить, что
.
То есть,
.
Пусть аналогичными рассуждениями мы установили, что нам достаточно доказать неравенство
.
Тогда
.
Раскрывая скобки и приводя подобные слагаемые, получим, что
.
Используя оценку и деля на положительный
элемент 
, получаем
.
Обозначим 
. Рассмотрим отображение 
, заданное по правилу 
. При 
, 
. Отображение является
сжимающим. Оно имеет единственную неподвижную точку. Найдем ее: 
. Откуда 
. Заметим, что 
. Последовательность 
стремится к 4. То есть, нам
достаточно установить, что 
, а это
следует из (*). Итак, мы доказали, что 
.
То есть, мы нашли такой многочлен, 
, что 
. Итак, мы доказали, что
если удовлетворяет минимальному
соотношению, являющемуся квадратным уравнением без положительных корней, то – поле. ■
Следствие 1. Если –
мнимый корень квадратного трехчлена, то ‑ поле.
Следствие 2. Любое простое расширение 
является полем 
, порожденным минимальным
соотношением 2 степени.
Доказательство.
Заметим, что 
. Покажем, что для любого aÎQ найдется такой квадратный многочлен , что 
- его корень многочлена.
Для этого достаточно представить 
.
Возьмем такой 
, что 
, тогда 
. Очевидно, 
. Таким образом, нам
удалось найти многочлен из . То
есть, 
- поле. ■
Рассмотрим последовательность действительных
чисел :
(**)
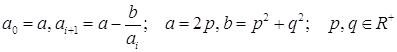Будем говорить, что последовательность 
задается числами p и q.
Лемма 2.3.3. Существует n, что 
.
Доказательство. Пусть 
.
Покажем, что последовательность 
убывающая.
,
то есть 
.
Пусть 
, тогда
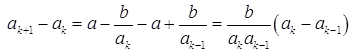
Так как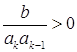 
,
то 
Пользуясь методом математической
индукции, заключаем, что 
, то
есть - убывающая.
Так как -
монотонно убывающая и ограничена снизу 0, то существует 
. Тогда 
.
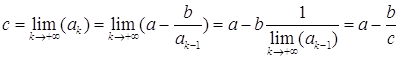То есть, 
.
Но тогда
,
,
что невозможно для 
. То есть, 
. ■
Лемма 2.3.4. Если 
,
то существует 
, что 
.
Доказательство. Запишем а и b в виде десятичных дробей:
, 
Так
как , то существует k, что 
и
.
Тогда 
.
Рассмотрим число 
.
То есть, . ■
Теорема 2.3.5. Если 
и 
, то
.
Доказательство. По лемме 2.3.3, 
. Пусть 
.
Если n=1, то 
. Рассмотрим 
.
То есть,
.
Так как .
По лемме 2.3.4 
. Тогда
.
Рассмотрим n > 1.
Пусть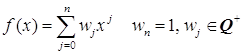 
.
Покажем, что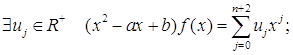 
Раскроем скобки и сгруппируем члены при xj.
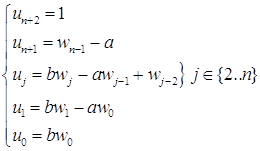
То есть,
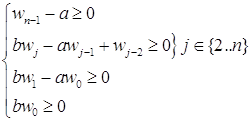
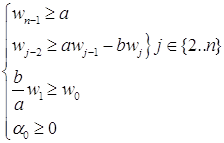
Заметим, что 
. Для существования 
, по лемме 2.3.4,
достаточно выполнения условий 
и 
, то есть, 
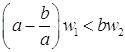. Обозначим 
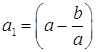. Так как 
, то 
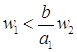и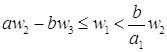 
. Для существования 
достаточно доказать
существование 
и 
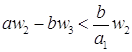. То есть, 
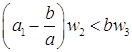. Обозначим 
. Повторим эту операцию n-2 раза. Получим, что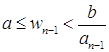 
. По лемме 2.3.4, 
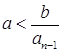существует, если 
и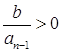 
. Эти условия следуют из того,
что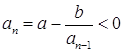 
и 
.
Таким образом, доказано существование
■
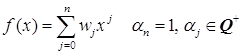
Теорема 2.3.6. Если минимальный многочлен f-g порождает полуполе то, он либо имеет
положительный действительный корень, либо корень ,
такой что и последовательность (**),
заданная числами p и q, не
содержит отрицательных элементов.
Доказательство. Пусть многочлен f-g не имеет положительных действительных корней, и для всех
корней вида , где 
, последовательность
(**), заданная числами p
и q, содержит отрицательный элемент. Тогда, по теореме 2.3.5, для каждого множителя вида 
существует многочлен 
, что 
. Рассмотрим многочлен 
. 
так как 
и 
. Кроме того 
, а остальные множители
многочлена 
имеют вид 
или 
. То есть, 
. Таким образом 
. По теореме 2.1.1,
минимальный многочлен порождает поле. ■
Теорема 2.3.7. Для комплексных чисел расширение , минимальное
соотношение которого имеет положительный корень, является полуполем.
Доказательство. Пусть a' – положительный корень минимального соотношения.
Предположим, что – поле. Тогда
существует многочлен f с
положительными коэффициентами, делящийся на минимальный многочлен. Значит f(a')=0. Но 
. Значит
a' – не является корнем многочлена f. То есть –
полуполе. ■
2.4. Примеры
1. Рассмотрим 
. Оно удовлетворяет
минимальному соотношению 
. По теореме
2.3.7, - полуполе. Аналогично доказывается,
что 
– полуполе.
2. 
– полуполе. Для доказательства нужно
воспользоваться теоремой 2.3.1.
3. Покажем, что 
– полуполе. Во-первых,
заметим, что 
. Рассмотрим 
. По теореме 2.3.7, 
‑ полуполе.
Тогда, по теореме 2.3.1, –
полуполе. 
. То есть, – полуполе.
4. , минимальное соотношение которого
имеет вид 
, есть полуполе. Действительно,
многочлен имеет положительный корень,
а значит - полуполе.
Теперь приведем примеры полей.
5. 
является полем, потому что его
минимальный многочлен имеет вид 
.
6. Пусть удовлетворяет
минимальному соотношению 
. Его
минимальный многочлен 
делит 
. То есть, 
– поле. Несложно видеть,
что 
. Итак, 
.
7. Пусть удовлетворяет
минимальному соотношению 
. Тогда
– поле.
8. Пусть 
,
если 
, то – поле. Так как , то 
Если , то 
. Рассмотрим
последовательность (**), порожденную p и q.
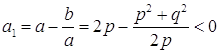. По теореме 2.3.7, – поле.
Литература
1. Вечтомов Е.М. Введение в полукольца. – Киров: Изд-во Вятского гос. пед. ун-та, 2000
2. Вечтомов Е.М. О свойствах полутел // Матем. вестник педвузов Волго-Вятского региона. – 2001, вып. 3. – Киров: Изд-во Вят. гос. пед. ун-та. – С. 11-20.
3. Ряттель А.В. Однопорожденные полукольца с делением // Матем. вестник педвузов Волго-Вятского региона. – 2002, вып. 4.– Киров: Изд-во Вятского госпедуниверситета. – С. 39-45.