Контрольная работа: Полурешетки m-степеней

Сейчас много внимания уделяется вопросам сводимости функций. Данная работа посвящена одной из разновидностей сводимости частично рекурсивной функции, а именно m-сводимости.

Для дальнейшего рассмотрения этого вопроса будем пользоваться общепринятыми понятиями и теоретико-множественными обозначениями.

Символы логических операций: отрицания, конъюнкции, дизъюнкции, импликации, и эквивалентности будем обозначать: , соответственно.

Кванторы общности и существования обозначают  соответственно.

Совокупность всех целых неотрицательных чисел обозначим через N.

Под множеством будем понимать подмножество N.

Латинскими буквами A,B,C,… будем обозначать множества.

Объединение множества A и B обозначим через пересечения этих множеств -  а разность , дополнение - .

Пусть 1*2*…*n 1,2,…,n11, 22,…,nn-декартово произведение множеств 1,2,…,n.

Определение: Функции  называется арифметической, если ее аргументы пробегают натуральный ряд N, и сама функция принимает лишь натуральные значения.

Под n-местной  частичной арифметической функцией будем понимать функцию, отображающую некоторое множество  в N ,где  -n-ая декартовая степень множества N.

Греческими строчными буквами будем обозначать частично рекурсивные функции (ЧРФ) :  .

Всякий раз, когда число аргументов явно не указывается, речь идет об одноместных функциях. Обозначим через  множество всех одноместных ЧРФ.

Запись  означает, что функция для этой n-ки  не определена, а запись  означает, что функция для этой n-ки определена.

Множество  называют областью значений функции , а множество  область определения функции .

Определение: Частичную n-местную функцию  назовем всюду определенной, если .

Всюду определенная функция будет обозначаться латинскими буквами: f,g,h,… . [5,6]


Теоретическая часть

 

§1 Основные определения

Определение 1: (интуитивное).

Арифметическая функция называется частично рекурсивной, если существует алгоритм для нахождения ее значений.

Определение 2:

Под начальными функциями будем понимать следующие функции:

1. функция следования S ;

2. функции выбора

,

3.

4. нулевая функция  .

Определение 3: (оператор суперпозиции (подстановка)).

Говорят, что функция  получена суперпозицией из функций  и , если для всех значений выполняется равенство:

Определение 4: (оператор примитивной рекурсии ).

Говорят, что функция  получена из двух функций  и  с помощью оператора примитивной рекурсии, если имеют место следующие равенства:


.

Это определение применимо и при n=0. Говорят, что функция  получена из одноместной функции константы равной  и функции , если при всех :

Определение 5: (-оператор или оператор минимизации).

Определим -оператор сначала для одноместных функций.

Будем говорить, что функция  получена из частичной функции  с помощью оператора, если,

.

В этом случае -оператор называется оператором обращения и -наименьшее .

Теперь определим -оператор в общем виде:

Определение 6:

Функция  называется частично рекурсивной функцией (ЧРФ) ,если она может быть получена из начальных функций с помощью конечного числа применений трех операторов: суперпозиции, примитивной рекурсии, -оператора.

Определение 7:

Если  - ЧРФ и всюду определена, то она называется рекурсивной функцией.

Определение 8:

Множество  - рекурсивно перечислимо (РП), в интуитивном смысле, если существует эффективная процедура, которая выписывает элементы этого множества. Каждый элемент  на некотором шаге будет выписан.

Определение 9:

Характеристической функцией множества называется функция

Определение 10:

Множество  называется рекурсивным, если характеристическая функция  является рекурсивной.

Определение 11:

Функция  m-сводима к функции (), в точности тогда, когда существует рекурсивная функция , такая, что

Функция  называется сводящей функцией.

Введем отношение m-эквивалентности на множестве .

Определение 12:

Введем понятие m-степени функции .

Определение 13:

Введем понятие m-сводимости множеств.

Определение 14:

Множество  m-сводимо к множеству  (обозначение ), если существует рекурсивная функция  такая, что  В этом случае говорят, что m-сводимо к  посредством .

Аналогично вводится понятие m-степени множества .

Определение 15:

Частичная характеристическая функция для множества  -функция

 

Определение 16:

ЧРФ – универсальная для множества , если (-рекурсивная функция )  где  - ЧРФ с геделевым номером .

Определение 17:

Если на множестве  определено бинарное отношение , удовлетворяющее условиям:

1.  (рефлексивность);

2.  (антисимметричность);

3.  (транзитивность),

то множество  называется частично упорядоченным, а отношение  называется частичным порядком на . Отношение , удовлетворяющее только свойствам 1,3, называется предпорядком на . Если частичный порядок  на удовлетворяет условию

4.  то  называется линейным порядком (или просто порядком), а -линейно упорядоченным множеством или цепью.

Определение 18:

Верхней (нижней) гранью подмножества  называется такой элемент  что  () для любого . Элемент  называется max (min) элементом , если  () для всех

Если же  () для любых ?  ,то элемент  называется наибольшим (наименьшим).

Определение 19.

Наименьшая (наибольшая) из верхних (нижних) граней множества  называется точной верхней (нижней) гранью этого множества.

Определение 20.

Полурешеткой (точнее, верхней полурешеткой) назовем пару  где - непустое множество, а -бинарная операция на , удовлетворяющая условиям: для любого

1.

2.   

3.

Если  - полурешетка, то зададим на  частичный порядок  следующим соотношением: для

Проверка того, что это частичный порядок, очевидна. Операция  является для этого порядка  операцией взятия точной верхней грани.

Определение 21:

Множество  называется продуктивным, если существует рекурсивная функция , называемая продуктивной функцией для , такая, что

Ясно, что продуктивное множество  не может быть р.п. Если бы  то Ø, что невозможно.

Определение 22:

Множество  называется креативным, если оно р.п. и  продуктивно.

Заметим, что креативные множества по теореме Поста не могут быть рекурсивными. Примером креативного множества будет

Действительно

откуда рекурсивная функция  является продуктивной функцией для .

Имеет место следующее утверждение: если В - р.п. множество, А -креативно, то - креативно. [1,5]

§2 Простейшие свойства m – степеней

Ведем отношение частного порядка на множестве m – степеней:


Обозначим через L частично упорядоченное множество m – степеней.

Утверждение 2.1: множество L является верхней полурешеткой.

Доказательство:

Рассмотрим , где

.

Докажем, что эта функция является точной верхней гранью для произвольных ЧРФ α и β.

Рассмотрим γ’:  

  для рекурсивных функций g, f.

Определим функцию .

Проверим следующие равенства: .

Пусть x=2t, тогда  и .

Пусть x=2t+1, тогда  и .

Таким образом, равенство  справедливо.

Следовательно, функция  является точной верхней гранью для произвольных ЧРФ α и β, ч.т.д.

Утверждение 2.2: .

Доказательство:

: Пусть , тогда  посредством рекурсивной функции f, которая множество А m – сводит к В.

: Аналогично , ч.т.д.

Следствие: существует изоморфное вложение полурешетки m-степеней рекурсивно перечисляемых множеств в полурешетку m-степеней частичных характеристических функций: .

Утверждение 2.3: .

Доказательство:

Если Ø, то утверждение справедливо.

Пусть Ø. Возьмем , откуда  для некоторого ; а так как  для некоторой рекурсивной функции f, то  и .

Таким образом, , ч.т.д.

Следствие: функции, принадлежащие одной и той же m-степени, имеют одинаковую область значений.

Утверждение 2.4: Пусть f, g – рекурсивные функции, тогда .

Доказательство:

 : Следует из следствия к 2.3.

 : Пусть : покажем, что , то есть .

Строим  таким образом: допустим , начинаем последовательно вычислять g(0), g(1), …, пока не получим, что g(n)=i, а такое n обязательно появится, так как .

Полагаем, что , тогда очевидно, что .

Аналогично строим функцию , такую, что . Отсюда получим, что .

Таким образом, так как  и , ч.т.д. [1]


§3 Минимальные элементы верхней полурешетки m-степеней

Утверждение 3.1: Наименьшего элемента в L нет.

Доказательство:

Допустим противное, то есть пусть  - наименьший в L элемент. Тогда Ø), где сØ – нигде неопределенная функция.

Следовательно, Ø и (сØ).

Возьмем всюду определенную функцию h. Ясно, что сØ≤mh.

С одной стороны, (сØ) – наименьший элемент, то есть сØ≤mh; с другой стороны сØ≤mh.

Получили противоречие, то есть в L наименьшего элемента нет. Ч.т.д.

Утверждение 3.2: m-степень, содержащая универсальную функцию, является наибольшей в L.

Доказательство:

Пусть Ψ – универсальная функция, а α – произвольная ЧРФ. Так как α – ЧРФ, то найдется такое число х0, что α=φ0.

Покажем, что . В качестве сводящей возмем функцию f(x0,y). Тогда из определения Ψ вытекает, что , где , то есть .

Таким образом,  - наибольшая в L. Ч.т.д.

Введем обозначение: .

Ясно, что .

Утверждение 3.3: сØ и множество всех функций вида cn(x) и только они образуют множество минимальных в L элементов.

Доказательство.

Из утверждения 3.1. следует, что сØ – минимальный в L элемент.

Возьмем произвольную функцию cn(x).

Пусть .

Ясно, что {}, кроме того α – всюду определенная функция, так как иначе , следовательно, .

Пусть теперь  минимальный в L элемент, отличный от сØ и от всех сn, тогда  определена в некоторой точке х0; пусть , имеем , где , то есть, . Получили противоречие. Ч.т.д. [1,2]


2. Практическая часть.

 

§1. Идеалы полурешетки m-степеней частично рекурсивных функций

Определение:

Идеалом полурешетки L назовем всякое подмножество I отличное от Ø, удовлетворяющее следующим условиям:

1. ;

2. .

Идеал называется главным, если он содержит наибольший элемент.

Рассмотрим множество всех m-степеней частичных характеристических функций, то есть:

Н={}.

Предположение 4.1:

Множество Н является главным идеалом полурешетки L.

Доказательство:

1.                  Берем две степени  для некоторых р.п. множеств А и В. точной верхней гранью будет степень, содержащая функцию .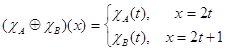

Определим множество АВ:

{}.


Докажем, что .

Будем пользоваться определением 15 для доказательства данного равенства.

Рассмотрим 4 случая.

1)     если x=2t,

И если x=2t,

2)     Если x=2t,

И если x=2t,

3)     Если x=2t+1,

И если x=2t+1,

4)     Если x=2t+1,

И если x=2t+1,

Следовательно, равенство  справедливо во всех четырех случаях, т.к. обе его части равносильны в рассмотренных случаях.

.

2.                  Пусть . По определению m-сводимости из  следует, что существует рекурсивная функция f такая, что: , откуда . Из утверждения 2.2 и того, что всякое р.п. множество m-сводимо к креативному следует, что:  - наибольший элемент в Н, где k – креативно.

Тогда Н – главный идеал полурешетки L. Ч.т.д.

Рассмотрим множество всех m-степеней рекурсивных функций, то есть:

М={}.

Предположение 4.2: Данное множество М является главным идеалом полурешетки L.

Доказательство:

1.                  Берем две степени рекурсивных функций, их точной верхней гранью будет , где  также рекурсивная функция.

2.                  Если , откуда существует рекурсивная функция h, такая, что , где  также рекурсивная функция. Далее,  посредством f(x) для любой рекурсивной функции f(x), отсюда  - наибольший элемент в М.

М – главный идеал полурешетки L. Ч.т.д.


Литература

1.       Дегтев А.Н. Сводимость частично-рекурсивных функций. – Сибирский математический журнал, 1975 т. 16, №5, с. 970-988.

2.       Ершов Ю.Л. Теория нумераций. – М.: Наука, 1977.

3.       Кагленд Н. Вычислимость. Введение в теорию рекурсивных функций. – М.: Мир, 1983.

4.       Мальцев А.И. Алгоритмы и рекурсивные функции. – М.: Наука, 1965.

5.       Поляков Е.А., Розинас М.Г. Теория алгоритмов. – Иваново: ИвГУ, 1976.

6.       Поляков Е.А., Маринина Н.В. Теория алгоритмов. – Шуя: ШГПУ, 2004.

7.       Роджерс Х. Теория рекурсивных функций и эффективная вычислимость. – М.: Мир, 1972.


  • Заказ
  • Оплата
  • Соцсети
  • Каталог
  • Карта сайта
  • Гарантии
  • Антиплагиат
    • p;      Пусть . По определению m-сводимости из  следует, что существует рекурсивная функция f такая, что: , откуда . Из утверждения 2.2 и того, что всякое р.п. множество m-сводимо к креативному следует, что:  - наибольший элемент в Н, где k – креативно.

    Тогда Н – главный идеал полурешетки L. Ч.т.д.

    Рассмотрим множество всех m-степеней рекурсивных функций, то есть:

    М={}.

    Предположение 4.2: Данное множество М является главным идеалом полурешетки L.

    Доказательство:

    1.                  Берем две степени рекурсивных функций, их точной верхней гранью будет , где  также рекурсивная функция.

    2.                  Если , откуда существует рекурсивная функция h, такая, что , где  также рекурсивная функция. Далее,  посредством f(x) для любой рекурсивной функции f(x), отсюда  - наибольший элемент в М.

    М – главный идеал полурешетки L. Ч.т.д.


    Литература

    1.       Дегтев А.Н. Сводимость частично-рекурсивных функций. – Сибирский математический журнал, 1975 т. 16, №5, с. 970-988.

    2.       Ершов Ю.Л. Теория нумераций. – М.: Наука, 1977.

    3.       Кагленд Н. Вычислимость. Введение в теорию рекурсивных функций. – М.: Мир, 1983.

    4.       Мальцев А.И. Алгоритмы и рекурсивные функции. – М.: Наука, 1965.

    5.       Поляков Е.А., Розинас М.Г. Теория алгоритмов. – Иваново: ИвГУ, 1976.

    6.       Поляков Е.А., Маринина Н.В. Теория алгоритмов. – Шуя: ШГПУ, 2004.

    7.       Роджерс Х. Теория рекурсивных функций и эффективная вычислимость. – М.: Мир, 1972.