Дипломная работа: Развитие понятия "Пространство" и неевклидова геометрия
Оглавление
Введение
Глава I. Развитие геометрии
1.1 История геометрии
1.2 Постулаты Евклида
1.3 Аксиоматика Гильберта
1.4 Другие системы аксиом геометрии
Глава II. Неевклидовы геометрии в системе Вейля
2.1 Элементы сферической геометрии
2.2 Эллиптическая геометрия на плоскости
2.3 Геометрия Лобачевского в системе Вейля
2.4 Различные модели плоскости Лобачевского. Независимость 5-го постулата Евклида от остальных аксиом Гильберта
Заключение
Список литературы
Введение
Любая теория современной науки считается единственно верной, пока не создана следующая. Это своеобразная аксиома развития науки.
Этот факт многократно подтверждался. Физика Ньютона переросла в релятивистскую физику, а та в квантовую. Теория флогистона стала химией, а самозарождение мышей из грязи обернулось биологией. Такова судьба всех наук, и нельзя сказать, что сегодняшнее открытие через двадцать лет не окажется грандиозной ошибкой. Но это тоже нормально – ещё Ломоносов говорил: «Алхимия – мать химии: дочь не виновата, что её мать глуповата».
Участь эта не обошла и геометрию. Традиционная Евклидова геометрия переросла в неевклидову, геометрию Лобачевского. Именно этому разделу математики, его истории и особенностям и посвящен этот проект.
В своём реферате я хочу показать, что кроме геометрии, которую изучают в школе (Геометрии Евклида или употребительной геометрии), существует еще одна геометрия, геометрия Лобачевского. Эта геометрия существенно отличается от евклидовой, например, в ней утверждается, что через данную точку можно провести бесконечно много прямых, параллельных данной прямой, что сумма углов треугольника меньше 180 В геометрии Лобачевского не существует прямоугольников, подобных треугольников и так далее.
Я выбрал данную тему по нескольким причинам: теория геометрии Лобачевского помогает взглянуть по-другому на окружающий нас мир, это интересный, необычный и прогрессивный раздел современной геометрии, она дает материал для размышлений – в ней не все просто, не все ясно с первого взгляда, чтобы ее понять, нужно обладать фантазией и пространственным воображением. Ситуация с геометрией Лобачевского и геометрией Евклида во многом похожа на ситуацию с Теорией относительности Эйнштейна и классической физикой. Геометрия Лобачевского и ОТП Эйнштейна это прогрессивные взаимосвязанные теории, выполняющиеся на огромных величинах и расстояниях, и остающимися верными на приближениях к нулю. В пространственной модели ОТП используется не обычная евклидовая плоскость, а искривленное пространство, на котором верна теория Лобачевского.
Глава I. Развитие геометрии
1.1 История геометрии
Геометрия – это одна из древнейших наук. Исследовать различные пространственные формы издавна побуждало людей их практическая деятельность. Древнегреческий ученый Эдем Родосский в IV веке до нашей эры писал: «Геометрия была открыта египтянами, и возникла при измерении Земли. Это измерение было им необходимо вследствие разлития реки Нил, постоянно смывавшей границы. Нет ничего удивительного, что эта наука, как и другие, возникла из потребности человека».
Считается, что геометрия началась в так называемой Ионийской школе. Её основателем считается Фалес Милетский (640-540 (546?) гг. до н. э.). Он считался одним из семи мудрецов Греции, первым математиком, астрономом и философом. Он доказал, что углы при основании равнобедренного треугольника равны, что вертикальные углы равны, что диаметр делит окружность пополам и ещё множество теорем. Предсказание затмения солнца в 585 году также приписывается ему.
Огромный импульс развития этой школе дал Пифагор (569-470 гг. до н. э.). В основном о его личных качествах пишут то же самое, что и о Фалесе. Но к этому ещё можно добавить титул чемпиона по боксу на олимпийских играх – звание, среди математиков редкое.
Несмотря на все его достижения, мнение современников хорошо выразил Гераклит: «Многознание без разума». Что ж, это было вполне заслужено: Пифагор засекречивал открытия и приписывал себе работы учеников. Пифагор также заставлял своих воспитанников исполнять целый свод очень странных правил: например, не прикасаться к белому петуху.
Но факт есть факт - и одна из теорем Пифагора теперь известна каждому – это теорема о равенстве квадрата гипотенузы сумме квадратов катетов. Эта теорема настолько популярна в мире математиков, что одних только доказательств накопилось 39 штук. Их можно посмотреть на сайте www.cut-the-knot.com/pythagoras.
Платон (428-348) знаменит введением принципа дедуктивности в математике, или принципа развития от простого к сложному. Он также знаменит постановкой трех задач на построение. Используя только циркуль и линейку, надо было:
1. Разделить угол на три части (задача о трисекции угла).
2. Построить квадрат, равный по площади данному кругу (задача о квадратуре круга).
3. Построить куб, равный по объему данному (задача об удвоении куба).
Нерешаемость этих задач была доказана только в 19 веке, но перед этим они успели вызвать настоящую бурю: например, задача №2 вызвала появление интегрального исчисления.
Многие первоначальные геометрические сведения получили также шумеро-вавилонские, китайские и другие ученые древнейших времен. Устанавливались они сначала только опытным путем, без логических доказательств.
Как наука, геометрия впервые сформировалась в Древней Греции, когда геометрические закономерности и зависимости, найденные ранее опытным путем, были приведены в надлежащую систему и доказаны.
Закончилось развитие традиционной геометрии Евклидом. В III веке до нашей эры греческий ученый привел в систему известные ему геометрические сведения в большом сочинении «Начала».
Его книга «Начала» только до 1880 года выдержала 460 изданий, уступив только Библии. Способ построения «Начал» стал единственно верным для всех научных работ: Перечисление основных, естественных понятий ® Перечисление основных аксиом ® Перечисление основных определений ® Формулирование теорем (утверждений) и их доказательство.
Метод доказательства от противного – тоже его заслуга. Он же сформулировал пять постулатов геометрии:
1. Через два точки можно провести одну и только одну прямую.
2. Прямая продолжается бесконечно.
3. Из любого центра можно провести окружность любым радиусом.
4. Все прямые углы равны между собой.
Пятый постулат является своеобразным философским камнем геометрии.
Неевклидова геометрия появилась вследствие долгих попыток доказать V постулат Евклида, аксиому параллельности. Эта геометрия во многом удивительна, необычна и во многом не соответствует нашим привычным представлениям о реальном мире. Но в логическом отношении данная геометрия не уступает геометрии Евклида.
1.2 Постулаты Евклида
Евклид – автор первого дошедшего до нас строгого логического построения геометрии. В нем изложение настолько безупречно для своего времени, что в течение двух тысяч лет с момента появления его труда «Начал» оно было единственным руководством для изучающих геометрию.
«Начала» состоят из 13 книг, посвященных геометрии и арифметике в геометрическом изложении.
Каждая книга «Начал» начинается определением понятий, которые встречаются впервые. Так, например, первой книге предпосланы 23 определения. В частности,
Определение 1. Точка есть то, что не имеет частей.
Определение 2. Линия есть длины без ширины
Определение 3. Границы линии суть точки.
Вслед за определениями Евклид приводит постулаты и аксиомы, то есть утверждения, принимаемые без доказательства.
Постулаты
I. Требуется, чтобы от каждой точки ко всякой другой точке можно было провести прямую линию.
II . И чтобы каждую прямую можно было неопределенно продолжить.
III. И чтобы из любого центра можно было описать окружность любым радиусом.
IV. И чтобы все прямые углы были равны.
V. И чтобы всякий раз, когда прямая при пересечении с двумя другими прямыми образует с ними односторонние внутренние углы, сумма которых меньше двух прямых, эти прямые пересекались с той стороны, с которой эта сумма меньше двух прямых.
Аксиомы
I. Равные порознь третьему равны между собой.
II. И если к ним прибавим равные, то получим равные.
III. И если от равных отнимем равные, то получим равные.
IV. И если к неравным прибавим равные, то получим неравные.
V. И если удвоим равные, то получим равные.
VI. И половины равных равны между собой.
VII. И совмещающиеся равны.
VIII. И целое больше части.
IX. И две прямые не могут заключать пространства.
Иногда IV и V постулаты относят к числу аксиом. Поэтому пятый постулат иногда называют XI аксиомой. По какому принципу одни утверждения относятся к постулатам, а другие к аксиомам, неизвестно.
Никто не сомневался в истинности постулатов Евклида, что касается и V постулата. Между тем уже с древности именно постулат о параллельных привлек к себе особое внимание ряда геометров, считавших неестественным помещение его среди постулатов. Вероятно, это было связано с относительно меньшей очевидностью и наглядностью V постулата: в неявном виде он предполагает достижимость любых, как угодно далеких частей плоскости, выражая свойство, которое обнаруживается только при бесконечном продолжении прямых.
Возможно, что уже сам Евклид пытался доказать постулат о параллельных. В пользу этого говорит то обстоятельство, что первые 28 предложений «Начал» не опираются на V постулат. Евклид как бы старался отодвинуть применение этого постулата до тех пор, пока использование его не станет настоятельно необходимым.
Одни математики старались доказать постулат о параллельных, применяя только другие постулаты и те теоремы, которые можно вывести из последних, не используя сам V постулат. Все такие попытки оказались неудачными. Их общий недостаток в том, что в доказательстве неявно применялось какое-нибудь предположение, равносильное доказываемому постулату.
Другие предлагали по-новому определить параллельные прямые или же заменить V постулат каким-либо, по их мнению, более очевидным предложением. Так, например, в XI веке Омар Хайям ввел вместо V постулата «принцип», согласно которому две лежащие в одной плоскости сходящиеся прямые пересекаются и не могут расходиться в направлении схождения. С помощью этого принципа Хайям доказывает, что в четырехугольнике ABCD, в котором углы при основании А и В – прямые и стороны АС, ВD равны, углы С и D так же прямые, а из этого предложения о существовании прямоугольника выводится V постулат. Рассуждения Хайяма получили оригинальное развитие в XIII веке у Насирэдинна ат-Туси, работы которого в свою очередь стимулировали исследования Д. Валлиса. В 1663 году Валлис доказал постулат о параллельных, исходя из явного допущения, что для каждой фигуры существует подобная ей фигура произвольной величины. Это допущение он считал вытекающим из существа пространственных отношений.
С логической точки зрения результаты Хайяма или Валлиса лишь выявляли равносильность V постулата и некоторых других предложений геометрии. Так, Хайям, по существу, установил эквивалентность постулата и предложения о сумме углов треугольника, а Валлис показал, что не только из V постулата можно вывести учение о подобии, но и обратно – их евклидова учения о подобии следует V постулат.
Один из обнадеживающих способов подхода к доказательству пятого постулата, которым пользовались многие геометры XVIII и первой половины XIX веков, состоит в том, что пятый постулат заменяется его отрицанием или каким-либо утверждением, эквивалентным отрицанию. Опираясь на измененную таким образом систему постулатов и аксиом, доказываются всевозможные предложения, логически из нее вытекающие. Если пятый постулат действительно вытекает из остальных постулатов и аксиом, то измененная указанным образом система постулатов ми аксиом противоречива. Поэтому рано или поздно мы придем у двум взаимно исключающим выводам. Этим и будет доказан пятый постулат.
Именно таким путем пытались доказать пятый постулат Д. Саккери (1667-1733), И. Г. Ламберт (1728-1777) и А.М. Лежандр (1752-1833).
Исследования Саккери были опубликованы в 1733 году под названием «Евклид, очищенный от всяких пятен, или опыт, устанавливающий самые первые принципы универсальной геометрии».
Саккери исходил из
рассмотрения четырехугольника ![]() с двумя
прямыми углами при основании
с двумя
прямыми углами при основании![]() и с
двумя равными боковыми сторонами
и с
двумя равными боковыми сторонами ![]() и
и ![]() . Из симметрии фигуры
относительно перпендикуляра
. Из симметрии фигуры
относительно перпендикуляра ![]() к
середине основания
к
середине основания ![]() следует, что углы
при вершинах
следует, что углы
при вершинах ![]() и
и ![]() равны. Если принять пятый
постулат и, следовательно, евклидову теорию параллельных, то можно установить,
что углы
равны. Если принять пятый
постулат и, следовательно, евклидову теорию параллельных, то можно установить,
что углы ![]() и
и ![]() прямые и
прямые и ![]() - прямоугольник. Обратно,
как доказывает Саккери, если хотя бы в одном четырехугольнике указанного вида
углы при верхнем основании окажутся прямыми, то будет иметь место евклидов
постулат о параллельных. Желая доказать этот постулат Саккери делает три
возможных предположения: либо углы
- прямоугольник. Обратно,
как доказывает Саккери, если хотя бы в одном четырехугольнике указанного вида
углы при верхнем основании окажутся прямыми, то будет иметь место евклидов
постулат о параллельных. Желая доказать этот постулат Саккери делает три
возможных предположения: либо углы ![]() и
и ![]() прямые, либо тупые, либо
острые (гипотезы прямого, острого и тупого угла). Для доказательства пятого
постулата необходимо опровергнуть гипотезы острого и тупого угла. Совершенно
точными рассуждениями Саккери приводит к противоречию гипотезу тупого угла.
Вслед за тем, приняв гипотезу острого угла, он выводит весьма далеко идущие ее
следствия с тем, чтобы и здесь получить противоречие. Развивая эти следствия
Саккери строит сложную геометрическую систему, не заключая о противоречии
только потому, что полученные им выводы не соответствуют привычным
представлениям о расположении прямых. В результате он «находит» логическое
противоречие, но в результате вычислительной ошибки.
прямые, либо тупые, либо
острые (гипотезы прямого, острого и тупого угла). Для доказательства пятого
постулата необходимо опровергнуть гипотезы острого и тупого угла. Совершенно
точными рассуждениями Саккери приводит к противоречию гипотезу тупого угла.
Вслед за тем, приняв гипотезу острого угла, он выводит весьма далеко идущие ее
следствия с тем, чтобы и здесь получить противоречие. Развивая эти следствия
Саккери строит сложную геометрическую систему, не заключая о противоречии
только потому, что полученные им выводы не соответствуют привычным
представлениям о расположении прямых. В результате он «находит» логическое
противоречие, но в результате вычислительной ошибки.
Идеи Ламберта, развитые им в сочинении «теория параллельных линий» (1766г.), близко примыкают к соображениям Саккери.
Он рассматривает четырехугольник с тремя прямыми углами. Относительно четвертого угла так же возникают три гипотезы: этот угол прямой, тупой или острый. Доказав эквивалентность пятого постулата гипотезе прямого угла и сведя к противоречию гипотезу тупого угла, Ламберт, подобно Саккери, вынужден заниматься гипотезой острого угла. Она приводит Ламберта к сложной геометрической системе, в которой ему не удалось встретить логического противоречия. Ламберт нигде в своем сочинении не утверждает, что V постулат им доказан, и приходит к твердому заключению, что и все другие попытки в этом направлении не привели к цели.
«Доказательства евклидова постулата, - пишет Ламберт, - могут быть доведены столь далеко, что остается, по-видимому, ничтожная мелочь. Но при тщательном анализе оказывается, что в этой кажущейся мелочи и заключается вся суть вопроса; обыкновенно она содержит либо доказываемое предложение, либо равносильный ему постулат».
Более того, развивая систему гипотезы острого угла, Ламберт обнаруживает аналогию этой системы со сферической геометрией и в этом усматривает возможность ее существования.
«Я склонен даже думать, что третья гипотеза справедлива на какой-нибудь мнимой сфере. Должна же быть причина, вследствие которой она на плоскости далеко не поддается опровержению, как это легко может быть сделано со второй гипотезой».
Лежандр в своем доказательстве пятого постулата рассматривает три гипотезы относительно суммы углов треугольника.
1. Сумма углов треугольника равна двум прямым.
2. Сумма углов треугольника больше двух прямых.
3. Сумма углов треугольника меньше двух прямых.
Он доказал, что первая гипотеза эквивалентна пятому постулату, вторая гипотеза невозможна; и приняв третью гипотезу приходит к противоречию, неявно воспользовавшись в доказательстве пятым постулатом через один из его эквивалентов.
В результате проблема параллельных оставалась к началу XIX века неразрешенной и положение казалось безвыходным. Большой знаток вопроса венгерский математик Фаркаш Бояи в 1820 году писал своему сыну Яношу: «Молю тебя, не делай только и ты попыток одолеть теорию параллельных линий: ты затратишь на это все свое время, а предложения этого вы не докажете все вместе. Не пытайся одолеть теорию параллельных линий ни тем способом, который ты сообщаешь мне, ни каким-либо другим. Я изучил все пути до конца: я не встретил ни одной идеи, которой бы я не разрабатывал. Я прошел весь беспросветный мрак этой ночи, и всякий светоч, всякую радость жизни я в ней похоронил… Этот беспросветный мрак… никогда не прояснится на земле, и никогда несчастный род человеческий не будет владеть чем-либо совершенным даже в геометрии. Это большая и вечная рана в моей душе…». Беспросветный мрак, о котором с горечью писал старший Бойяи, рассеял Лобачевский и, несколько позднее, Я. Бояи.
Но многовековые попытки доказательства пятого постулата Евклида привели в конце концов к появлению новой геометрии, отличающейся от евклидовой тем, что в ней V постулат не выполняется. Эта геометрия теперь называется неевклидовой, а в России носит имя Лобачевского, который впервые опубликовал работу с ее изложением.
И одной из предпосылок геометрических открытий Н. И. Лобачевского (1792-1856) был как раз его материалистический подход к проблемам познания. Лобачевский Он был твердо уверен в объективном и не зависящем от человеческого сознания существовании материального мира и в возможности его познания. В речи «О важнейших предметах воспитания» (Казань, 1828) Лобачевский сочувственно приводит слова Ф. Бэкона: «оставьте трудиться напрасно, стараясь извлечь из одного разума всю мудрость; спрашивайте природу, она хранит все истины и на все вопросы ваши будет отвечать вам непременно и удовлетворительно». В своем сочинении «О началах геометрии», являющемся первой публикацией открытой им геометрии, Лобачевский писал: «первые понятия, с которых начинается какая-нибудь наука, должны быть ясны и приведены к самому меньшему числу. Тогда только они могут служить прочным и достаточным основанием учения. Такие понятия приобретаются чувствами; врожденным – не должно верить». Тем самым Лобачевский отвергал идею об априорном характере геометрических понятий, поддерживавшуюся И. Кантом.
Первые попытки Лобачевского доказать пятый постулат относятся к 1823 году. К 1826 году он пришел к убеждению в том, что V постулат не зависит от остальных аксиом геометрии Евклида и 11(23) февраля 1826 года сделал на заседании факультета казанского университета доклад «Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных», в котором были изложены начала открытой им «воображаемой геометрии», как он называл систему, позднее получившую название неевклидовой геометрии. Доклад 1826г. вошел в состав первой публикации Лобачевского по неевклидовой геометрии – статьи «О началах геометрии», напечатанной в журнале Казанского университета «Казанский вестник» в 1829-1820гг. дальнейшему развитию и приложениям открытой им геометрии были посвящены мемуары «Воображаемая геометрия», «Применение воображаемой геометрии к некоторым интегралам» и «Новые начала геометрии с полной теорией параллельных», опубликованные в «Ученых записках» соответственно в 1835, 1836 и 1835-1838 гг. Переработанный текст «Воображаемой геометрии» появился во французском переводе в Берлине, там же в 1840г. вышли отдельной книгой на немецком языке «Геометрические исследования по теории параллельных линий» Лобачевского. Наконец, в 1855 и 1856 гг. он издал в Казани на русском и французском языках «Пангеометрию».
Высоко оценил «Геометрические исследования» Гаусс, который провел Лобачевского (1842) в члены-корреспонденты Геттингенского ученого общества, бывшего по существу Академией наук ганноверского королевства. Однако в печати в оценкой новой геометрической системы Гаусс не выступил.
Высокая оценка гауссом открытия Лобачевского была связана с тем, что Гаусс, еще с 90-х годов XVIII в. занимавшийся теорией параллельности линий ,пришел к тем же выводам, что и Лобачевский. Свои взгляды по этому вопросу Гаусс не публиковал, они сохранились только в его черновых записках и в немногих письмам к друзьям. В 1818 г. в письме к австрийскому астроному Герлингу (1788-1864) он писал: «Я радуюсь, что вы имеете мужество высказаться так, как если бы Вы признавали ложность нашей теории параллельных, а вместе с тем и всей нашей геометрии. Но осы, гнездо которых Вы потревожите, полетят Вам на голову»; по-видимому, под «потревоженными осами» Гаусс имел в виду сторонников традиционных взглядов на геометрию, а также априоризма математических понятий.
Независимо от Лобачевского и гаусса к открытию неевклидовой геометрии пришел венгерский математик Янош Бояи (1802-1860), сын Ф. Бояи.
Когда Я. Бояи пришел к тем же идеям, что Лобачевский и Гаусс, отец не понял его, однако предложил напечатать краткое изложение его открытия в виде приложения к своему руководству по математике, вышедшему в 1832г. Полное название труда Я. Бояи – «Приложение, содержащее науку о пространстве, абсолютно истинную, не зависящую от истинности или ложности XI аксиомы Евклида (что a priori никогда решено быть не может)» и его обычно коротко называют просто «Аппендикс». Открытие Я. Бояи не было признано при его жизни; Гаусс, которому Ф. Бояи послал "Аппендикс", понял его, но никак не способствовал признанию открытия Я. Бояи.
1.3 Аксиоматика Гильберта
Хотя в современном аксиоматическом изложении геометрии Евклида не всегда пользуются аксиоматикой Гильберта, приведём её, как первую полную, независимую и непротиворечивую систему аксиом.
Все двадцать аксиом системы Гильберта подразделены на пять групп.
· Группа I содержит восемь аксиом принадлежности.
· Группа II содержит четыре аксиомы порядка.
· Группа III содержит пять аксиом конгруэнтности.
· Группа IV содержит две аксиомы непрерывности.
· Группа V содержит одну аксиому параллельности.
Переходим к формулировке аксиом по группам. Одновременно будем указывать некоторые утверждения, вытекающие из формулируемых аксиом.
I. Аксиомы принадлежности
I, 1. Каковы бы ни были две точки A и B, существует прямая a, которой принадлежат эти точки.
I, 2. Каковы бы ни были две точки A и B, существует не более одной прямой, которой принадлежат эти точки.
I, 3. Каждой прямой a принадлежат по крайней мере две точки. Существуют по крайней мере три точки, не принадлежащие одной прямой.
Указанные три аксиомы исчерпывают список аксиом принадлежности планиметрии. Следующие пять аксиом вместе с указанными тремя завершают список аксиом принадлежности стереометрии.
I, 4. Каковы бы ни были три точки A, B и C, не принадлежащие одной прямой, существует плоскость α, которой принадлежат эти три точки. Каждой плоскости принадлежит хотя бы одна точка.
I, 5. Каковы бы ни были три точки A, B и C, не принадлежащие одной прямой, существует не более одной плоскости, которой принадлежат эти точки.
I, 6. Если две принадлежащие прямой a различные точки A и B принадлежат некоторой плоскости α, то каждая принадлежащая прямой a точка принадлежит указанной плоскости.
I, 7. Если существует одна точка A, принадлежащая двум плоскостям α и β, то существует по крайней мере ещё одна точка B, принадлежащая обоим этим плоскостям.
I, 8. Существуют по крайней мере четыре точки, не принадлежащие одной плоскости.
С целью использования привычной для нас геометрической лексики договоримся отождествлять между собой следующие выражения: 1) «точка А принадлежит прямой a (плоскости α)», 2) «прямая а (плоскость α) проходит через точку А» 3) «точка А лежит на прямой а (плоскости α)» 4) «точка А является точкой прямой а (плоскости α)» и тому подобные.
Теорема 1. Две различные прямые не могут иметь больше одной общей точки.
Теорема 2. Две плоскости либо совсем не имеют общих точек, либо имеют общую прямую, на которой лежат все их общие точки.
Теорема 3. Плоскость и не лежащая на ней прямая не могут иметь более одной общей точки.
Теорема 4. Через прямую и не лежащую на ней точку, или через две различные прямые с общей точкой проходит одна и только одна плоскость.
Теорема 5. Каждая плоскость содержит по крайней мере три точки.
II. Аксиомы порядка
II, 1. Если точка B прямой а лежит между точками А и С той же прямой, то А, В и С – различные точки указанной прямой, причем В лежит также и между С и А.
II, 2. Каковы бы ни были две различные точки А и С, на определяемой ими прямой существует по крайней мере она точка В такая, что С лежит между А и В.
II, 3. Среди любых трёх точек, лежащих на одной прямой существует не более одной точки, лежащей между двумя другими.
Сформулированные три аксиомы относятся к расположению объектов на прямой и потому называются линейными аксиомами порядка. Формулируемая ниже последняя аксиома порядка относится к расположению геометрических объектов на плоскости. Для того, чтобы сформулировать эту аксиому, введём понятие отрезка.
Пару различных точек А и В назовём отрезком и будем обозначать символом АВ или ВА. Точки прямой, определяемой А и В, лежащие между ними, будем называть внутренними точками, или просто точками отрезка АВ. Остальные точки указанной прямой будем называть внешними точками отрезка АВ.
II, 4 (Аксиома Паша). Если А, В и С – три точки, не лежащие на одной прямой, и а – некая прямая в плоскости, определяемой этими точками, не содержащая ни одной из указанных точек и проходящая через некоторую точку отрезка АВ, то эта прямая проходит также либо через некоторую точку отрезка АС, либо через некоторую точку отрезка ВС.
Подчеркнём, что из одних аксиом порядка II, 1 – 4 ещё не вытекает, что любой отрезок имеет внутренние точки. Однако привлекая ещё аксиомы принадлежности I, 1 – 3 можно доказать следующее утверждение:
Теорема 6. Каковы бы ни были две различные точки А и В на прямой, ими определяемой, существует по крайней мере одна точка С, лежащая между А и В.
Теорема 7. Среди любых трёх точек одной прямой всегда существует одна точка, лежащая между двумя другими.
Теорема 8. Если точки А, В и С не принадлежат одной прямой и если некоторая прямая а пересекает[1] какие-либо два из отрезков АВ, ВС и АС, то эта прямая не пересекает третий из указанных отрезков.
Теорема 9. Если В лежит на отрезке АС, и С – на отрезке ВD, то В и С лежат на отрезке АD.
Теорема 10. Если С лежит на отрезке АD, а В – на отрезке АС, то В лежит также на отрезке АD, а С – на отрезке BD.
Теорема 11. Между любыми двумя точками прямой существует бесконечно много других её точек.
Теорема 12. Пусть каждая из точек С и D лежит между точками А и В. Тогда если М лежит между С и D, то М лежит и между А и В.
Теорема 13. Если точки С и D лежат между точками А и В, то все точки отрезка СD принадлежат отрезку АВ (в этом случае мы будем говорить, что отрезок СD лежит внутри отрезка АВ).
Теорема 14. Если точка С лежит между точками А и В, то 1) никакая точка отрезка АС не может быть точкой отрезка CВ, 2) каждая отличная от С точка отрезка АВ принадлежит либо отрезку АС, либо отрезку СВ.
Указанные утверждения позволяют упорядочить множество точек любой прямой и выбрать на этой прямой направление.
Будем говорить, что две различные точки А и В прямой a лежат по разные стороны (по одну сторону) от третьей точки О той же прямой, если точка О лежит (не лежит) между А и В.
Из указанных выше утверждений вытекает следующая теорема.
Теорема 15. Произвольная точка О каждой прямой а разбивает все остальные точки этой прямой на два непустых класса так, что любые две точки прямой а, принадлежащие одному и тому же классу, лежат по одну сторону от О, а любые две точки, принадлежащие разным классам, лежат по разные стороны от О.
Таким образом, задание на любой прямой двух различных точек О и Е определяет на этой прямой луч или полупрямую ОЕ, обладающую тем свойством, что любая её точка и точка Е лежат по одну сторону от О.
Выбрав на прямой а две различные точки О и Е, мы можем теперь определить порядок следования точек на прямой по следующему правилу: 1) если А и В – любые точки луча ОЕ, то будем говорить, что А предшествует В, если А лежит между О и В, 2) будем говорить, что точка О предшествует любой точке луча ОЕ, 3) будем говорить, что любая точка, принадлежащая той же прямой и не принадлежащая лучу ОЕ, предшествует как точке О, так и любой точке луча ОЕ, 4) если А и В – любые точки, не принадлежащие лучу ОЕ, то мы будем говорить, что А предшествует В, если В лежит между А и О.
Легко проверить, что для выбранного нами порядка следования точек прямой а справедливо свойство транзитивности: если А предшествует В, а В предшествует С, то А предшествует С.
Аксиомы, приведённые выше, позволяют упорядочить и точки, принадлежащие произвольной плоскости α.
Теорема 16. Каждая прямая а, принадлежащая плоскости α, разделяет не лежащие на ней точки этой плоскости на два непустых класса так, что любые две точки А и В из разных классов определяют отрезок АВ, содержащий точку прямой а, а любые две точки А и А’ из одного класса определяют отрезок АА’, внутри которого не лежит ни одна точка прямой а.
В соответствие с утверждением этой теоремы мы можем говорить, что точки А и А’ (одного класса) лежат в плоскости α по одну сторону от прямой а, а точки А и В (разных классов) лежат в плоскости α по разные стороны от прямой а.
III. Аксиомы конгруэнтности
III, 1. Если А и В – две точки на прямой а, А’ – точка на той же прямой или на другой прямой а’, то по данную от точки А’ сторону прямой а’ найдется, и притом только одна, точка В’ такая, что отрезок А’B’ конгруэнтен отрезку АВ. Каждый отрезок АВ конгруэнтен отрезку ВА.1
III, 2. Если отрезки А’B’ и А”B” конгруэнтны одному и тому же отрезку АВ, то они конгруэнтны и между собой.
III, 3. Пусть АВ и ВС – два отрезка прямой а, не имеющие общих внутренних точек, А’B’ и B’C’ – два отрезка той же прямой, или другой прямой а’, также не имеющие общих внутренних точек. Тогда если отрезок АВ конгруэнтен отрезку А’B’, а отрезок ВС конгруэнтен отрезку B’C’, то отрезок АС конгруэнтен отрезку А’C’.
Сформулированные три аксиомы относятся к конгруэнтности отрезков. Для формулировки следующих аксиом нам понадобятся понятие угла и его внутренних точек.
Пара полупрямых h и k, выходящих из одной и той же точки О и не лежащих на
одной прямой, называется углом и обозначается символом ![]() или
или ![]() .
.
Если полупрямые задаются
двумя своими точками ОА и ОВ, то мы будем обозначать угол символом ![]() или
или ![]() . В силу теоремы 4 любые
два луча h и k, составляющие угол
. В силу теоремы 4 любые
два луча h и k, составляющие угол ![]() ,
определяют, и притом единственную, плоскость α.
,
определяют, и притом единственную, плоскость α.
Внутренними точками ![]() будем называть те точки
плоскости α, которые, во-первых, лежат по ту сторону от прямой, содержащей
луч h, что и любая точка луча k, и, во-вторых, лежат по ту сторону
от прямой, содержащей луч k, что
и любая точка луча h.
будем называть те точки
плоскости α, которые, во-первых, лежат по ту сторону от прямой, содержащей
луч h, что и любая точка луча k, и, во-вторых, лежат по ту сторону
от прямой, содержащей луч k, что
и любая точка луча h.
III, 4. Пусть даны ![]() на плоскости α, прямая
а’ на этой же или на какой-либо другой плоскости α’ и задана
определённая сторона плоскости α’ относительно прямой а’. Пусть h’ – луч прямой а’, исходящий из
некоторой точки О’. Тогда на плоскости α’ существует один и только один
луч k’ такой, что
на плоскости α, прямая
а’ на этой же или на какой-либо другой плоскости α’ и задана
определённая сторона плоскости α’ относительно прямой а’. Пусть h’ – луч прямой а’, исходящий из
некоторой точки О’. Тогда на плоскости α’ существует один и только один
луч k’ такой, что ![]() конгруэнтен
конгруэнтен ![]() , и при этом все
внутренние точки
, и при этом все
внутренние точки ![]() лежат по
заданную сторону от прямой а’. Каждый угол конгруэнтен самому себе.
лежат по
заданную сторону от прямой а’. Каждый угол конгруэнтен самому себе.
III, 5. Пусть А, В и С – три точки, не
лежащие на одной прямой, А’, B’ и С’ – другие три точки, также не лежащие на одной прямой.
Тогда если отрезок АВ конгруэнтен отрезку А’B’, отрезок АС конгруэнтен отрезку А’C’ и ![]() конгруэнтен
конгруэнтен
![]() , то
, то ![]() конгруэнтен
конгруэнтен ![]() и
и ![]() конгруэнтен
конгруэнтен ![]()
Договоримся теперь о сравнении неконгруэнтных отрезков и углов.
Будем говорить, что отрезок АВ больше отрезка А’B’, если на прямой, определяемой точками А и В, найдётся лежащая между этими точками точка С такая, что отрезок АС конгруэнтен отрезку А’В’. Будем говорить, что отрезок АВ меньше отрезка А’B’, если отрезок А’B’ больше отрезка АВ.
Символически тот факт, что отрезок АВ меньше отрезка А’B’ (конгруэнтен отрезку А’B’) будем записывать так:
АВ<A’B’ (AB=A’B’).
Будем говорить, что ![]() больше
больше ![]() , если в плоскости,
определяемой
, если в плоскости,
определяемой ![]() , найдётся луч ОС, все
точки которого являются внутренними точками
, найдётся луч ОС, все
точки которого являются внутренними точками ![]() ,
такой, что
,
такой, что ![]() конгруэнтен
конгруэнтен ![]() . Будем говорить, что
. Будем говорить, что ![]() меньше
меньше ![]() , если
, если ![]() больше
больше ![]() .
.
С помощью аксиом принадлежности, порядка и конгруэнтности можно доказать целый ряд теорем элементарной геометрии. Сюда относятся: 1) три широко известные теоремы о конгруэнтности (равенстве) двух треугольников, 2) теорема о конгруэнтности вертикальных углов, 3) теорема о конгруэнтности всех прямых углов, 4) теорема о единственности перпендикуляра, опущенного из точки на прямую, 5) теорема о единственности перпендикуляра, проведённого к данной точке прямой, 6) теорема о внешнем угле треугольника, 7) теорема о сравнении перпендикуляра и наклонной.
IV. Аксиомы непрерывности
С помощью аксиом принадлежности, порядка и конгруэнтности мы произвели сравнение отрезков, позволяющее заключить, каким из трёх знаков <, = или > связаны эти отрезки.
Указанных аксиом, однако, недостаточно 1) для обоснования возможности измерения отрезков, позволяющее поставить в соответствие каждому отрезку определённое вещественное число, 2) для обоснования того, что указанное соответствие является взаимно однозначным.
Для проведения такого обоснования следует присоединить к аксиомам I, II и III две аксиомы непрерывности.
IV, 1 (аксиома Архимеда). Пусть АВ и СD – произвольные отрезки. Тогда на прямой, определяемой точками А и В существует конечное число точек А1, А2, ..., Аn, расположенных так, что точка А1 лежит между А и А2, точка А2 лежит между А1 и А3, ..., точка Аn-1 лежит между Аn-2 и Аn, причём отрезки АА1, А1А2, ..., Аn-1An конгруэнтны отрезку CD и точка В лежит между А и Аn.
IV, 2 (аксиома линейной полноты). Совокупность всех точек произвольной прямой а нельзя пополнить новыми объектами (точками) так, чтобы 1) на пополненной прямой были определены соотношения «лежит между» и «конгруэнтен», определён порядок следования точек и справедливы аксиомы конгруэнтности III, 1 – 3 и аксиома Архимеда IV, 1, 2) по отношению к прежним точкам прямой определённые на пополненной прямой соотношения «лежит между» и «конгруэнтен» сохраняли старый смысл.
Присоединение к аксиомам I, 1 – 3, II и III, 1- 3 аксиомы Архимеда позволяет поставить в соответствие каждой точке произвольной прямой а определённое вещественное число х, называемое координатой этой точки, а присоединение ещё и аксиомы линейной полноты позволяет утверждать, что координаты всех точек прямой а исчерпывают множество всех вещественных чисел. Пользуясь этим, можно обосновать метод координат.
V. Аксиома параллельности
Самая последняя аксиома играет в геометрии особую роль, определяя разделение геометрии на две логически непротиворечивые и взаимно исключающие друг друга системы: евклидову и неевклидову геометрии.
В геометрии Евклида эта аксиома формулируется так.
V. Пусть а – произвольная прямая и А – точка, лежащая вне прямой а, тогда в плоскости α, определяемой точкой А и прямой а существует не более одной прямой, проходящей через А и не пересекающей а.
Долгое время геометры пытались выяснить, не является ли аксиома параллельности следствием всех остальных аксиом. Этот вопрос был решен Николаем Ивановичем Лобачевским, который доказал независимость аксиомы V от аксиом I – IV.
По-другому результат Лобачевского можно сформулировать так: если к аксиомам I – IV присоединить утверждение, отрицающее справедливость аксиомы V, то следствия всех этих положений будут составлять логически непротиворечивую систему (неевклидову геометрию Лобачевского).
Систему следствий, вытекающих из одних только аксиом I – IV обычно называют абсолютной геометрией. Абсолютная геометрия является общей частью как евклидовой, так и неевклидовой геометрий, ибо все предложения, которые могут быть доказаны только с помощью аксиом I – IV, верны как в геометрии Евклида, так и в геометрии Лобачевского.
Доказательство непротиворечивости аксиоматики Гильберта
Чтобы доказать непротиворечивость некоей теории Х, необходимо из материала другой, заведомо непротиворечивой, теории А построить такую модель, в которой выполняются все аксиомы теории Х. Если это удастся, теорию Х можно считать непротиворечивой. Следовательно, для того, чтобы доказать непротиворечивость гильбертовой системы, необходимо построить такую модель евклидовой геометрии, в которой выполнялись бы все аксиомы, предложенные Гильбертом.
Для построения такой модели, необходима вышеупомянутая заведомо непротиворечивая теория. В модели, построенной Гильбертом, такой теорией служит теория действительных чисел. Идея построения модели состояла в рассмотрении системы координат на плоскости. В такой системе каждой точке М плоскости соответствуют два числа х и у – её координаты. Чтобы понять суть построения модели забудем о плоскости и имеющейся на ней координатной системе, «точками» будем называть упорядоченные пары действительных чисел (х; у) т. е. пары (х; у) и (у; х) с различными х и у будем считать различными. Теперь попытаемся определить «прямую». Вспомним, что каждая прямая описывается в координатах линейным уравнением вида ax + by + c = 0, где хотя бы один из коэффициентов a и b отличен от нуля. Например, уравнение прямой, не параллельной оси ординат, имеет вид у = kx + l, или, что то же самое, ax + by + c = 0, где a = k, b = -1, c = l. Если же прямая параллельна оси ординат, ей соответствует уравнение x = p (т. е. уравнение ax + by + c = 0, где a = 1, b = 0, c = -p;). При этом если все коэффициенты уравнения ax + by + c = 0 умножить на одно и то же число k ≠ 0, то полученное уравнение будет описывать ту же прямую. Мы же в своей модели будем называть «прямой» любое линейное уравнение вида ax + by + c = 0, в котором хотя бы один из коэффициентов a и b отличен от нуля, причём коэффициенты рассматриваются с точностью до ненулевого множителя пропорциональности (при k ≠ 0 уравнения ax + by + c = 0 и (ak)x + (bk)y + kc = 0 считаются одной и той же прямой).
Далее, «точка» (х1; у1) лежит на «прямой», если числа х1 и у1 удовлетворяют указанному уравнению. Как видим, для определения «прямых», «точек» и расположения «точек» на «прямой» достаточно опереться на теорию действительных чисел. Легко проверить, что в указанной модели выполняются, например, такие аксиомы:
1. Через две различные «точки» проходит «прямая»
2. На «прямой» имеется не менее двух «точек»
Легко определить случай, при котором одна из трёх «точек» лежит на «прямой» «между» двумя другими. Когда A(x1; y1), B(x2; y2) и C(x3; y3) – три «точки», лежащие на одной «прямой», «точка» B считается расположенной «между» A и C при условии, что число x2 заключено между числами x1 и x3 (если x1 = x2 = x3, то y2 заключено между y1 и y3). Тогда очевидно, что
3. Из трёх «точек», лежащих на одной «прямой», одна и только одна расположена между двумя другими.
Выполняются и другие аксиомы порядка (в частности, аксиома Паша). Заметим, что мы специально не иллюстрируем содержание аксиом чертежами, поскольку при чисто аксиоматическом изложении не следует использовать привычные геометрические представления.
Будем говорить, что две «прямые» a1x + b1y + c1 = 0 и a2x + b2y + c2 = 0 «параллельны», если коэффициенты a1, b1 и a2, b2 пропорциональны. Это можно кратко записать равенством a1b2 – a2b1 = 0. Нетрудно проверить, что две «параллельные» «прямые» либо не имеют ни одной общей «точки», либо совпадают (в обычной геометрии тоже часто принимают, что прямая параллельна самой себе). Более того,
4. Через любую «точку» A1(x1; y1) проходит одна и только одна «прямая», параллельная данной «прямой» Ax + By + C = 0.
Иначе говоря, в указанной модели выполняется аксиома параллельности. Можно здесь говорить и о длинах отрезков, и о величинах углов. Например, «расстоянием» между двумя «точками» A1(x1; y1) и A2(x2; y2) называется число
A1A2 = ![]()
Далее, в привычной евклидовой геометрии справедлива теорема косинусов:
cos C = ![]()
(величина угла С равна арккосинусу правой части равенства. Можно возразить, что тригонометрические функции (и, в частности, косинус) определяются геометрически и обойтись без обычной евклидовой геометрии в данном случае невозможно. Однако это неверно. В математическом анализе доказывается, что функция cos x задаётся бесконечным рядом
cos x = ![]() ,
,
который сходится для любого действительного x. Таким образом, в рассматриваемой модели допустимо говорить и о расстояниях, и о величинах углов.
Так же легко проверить, что в ней выполняются и аксиомы конгруэнтности (в частности, первый и второй признаки равенства треугольников). В итоге все гильбертовы аксиомы (представляющие собой развитие и уточнение аксиом Евклида) в рассматриваемой модели выполняются. Это и означает, что система аксиом евклидовой геометрии условно непротиворечива. Другими словами, она непротиворечива, если непротиворечива теория действительных чисел.
1.4 Другие системы аксиом геометрии
Вернёмся, однако, к евклидовой геометрии. В настоящее время систему аксиом Гильберта часто заменяют эквивалентной ей системой. Мы приведём те группы аксиом одной такой системы, по которым она отличается от вышеизложенной системы (группы аксиом порядка и движения, заменяющей в этой системе группу аксиом конгруэнтности).
Преимущество этой системы заключается в том, что она позволяет проще и быстрее получить первоначальные геометрические факты, лучше, как многим кажется, описывает свойства основных геометрических объектов с точки зрения привычных представлений.
II. Аксиомы порядка
Будем полагать, что на прямой есть два направления, взаимно противоположных друг другу, и по отношению каждому из них каждая пара точек А и В находится в известном отношении, которое выражается словом «предшествовать». Это отношение обозначается знаком <, так что выражение «А предшествует В» можно символически записать так:
А < B.
Требуется, чтобы указанное отношение для точек на прямой удовлетворяло нижеследующим пяти аксиомам.
II, 1. Если А < В в одном направлении, то В < А в противоположном направлении.
II, 2. В одном из двух направлений А < В исключает В < А.
II, 3. В одном из двух направлений если А < В и В < С, то А < С.
II, 4. В одном из двух направлений для каждой точки В найдутся точки А и С такие, что А < B < C.
Каждое из утверждений аксиом II, 2 – 4 относится к одному из двух направлений на прямой. По аксиоме II, 1 оно верно также и для противоположного направления.
Прежде чем сформулировать последнюю аксиому, определим некоторые понятия. Пусть а – прямая и А – точка на ней. При фиксированном направлении на прямой точка А разбивает её на две части (полупрямые), для каждой точки Х одной из них Х < А, а для каждой точки Х другой полупрямой А < X. Очевидно, это разбиение прямой на части не зависит от выбранного на ней направления (аксиома II, 1).
Пусть А и В – две точки прямой а. Если для точки С прямой а выполняется условие А < C < В или В < C < А, то мы будем говорить, что точка С лежит между точками А и В. Очевидно, свойство точки лежать между двумя данными не зависит от направления на прямой. Часть прямой а, все точки которой лежат между А и В, мы будем называть отрезком АВ, а точки А и В – концами отрезка.
II, 5. Прямая а, лежащая в плоскости α, разбивает эту плоскость на две полуплоскости так, что если X и Y – две точки одной полуплоскости, то отрезок XY не пересекается с прямой а, если же X и Y принадлежат разным полуплоскостям, то отрезок XY пересекается с прямой а.
Из аксиом принадлежности (связи), которые в этой системе аксиом аналогичны аксиомам принадлежности Гильберта, и аксиом порядка выводятся следующие следствия.
Теорема 1. Среди точек А, В, С на прямой а одна и только одна лежит между двумя другими.
Теорема 2. Каждый отрезок содержит по крайней мере одну точку.
Теорема 3. Если В – точка отрезка АС, то отрезки АВ и ВС принадлежат АС, т. е. каждая точка отрезка АС и каждая точка отрезка ВС принадлежит отрезку АС.
Теорема 4. Если В – точка отрезка АС и X – точка того же отрезка, отличная от В, то она принадлежит либо отрезку АВ, либо ВС.
Теорема 5. Пусть α – плоскость, и а – лежащая на ней прямая, b – другая прямая, или полупрямая, или отрезок в той же плоскости α.
Тогда, если b не пересекает а, то все точки b лежат по одну сторону от а, т. е. в одной из полуплоскостей, определяемых прямой а.
Пусть А, В и С – три точки, не лежащие на одной прямой. Фигура, составленная из трёх отрезков АВ, ВС и АС называется треугольником, точки А, В и С – вершинами треугольника, а отрезки АВ, ВС и АС – сторонами треугольника.
Теорема 9. Пусть АВС – треугольник в плоскости α и а – прямая в этой плоскости, не проходящая ни через одну из точек А, В, С. Тогда если эта прямая пересекает сторону АВ, то она пересекает и притом только одну из двух других сторон ВС или АС.
Нельзя не заметить, что последняя приведённая теорема почти аналогична аксиоме Паша, входящей в систему Гильберта (см. страницу 9), и отличается от неё только тем, что в аксиоме не утверждается единственность второй пересекаемой стороны треугольника.
III. Аксиомы движения
В данной системе группа аксиом конгруэнтности заменена этой группой аксиом. Впрочем, третьи группы аксиом обоих систем в конечном итоге выполняют одну и ту же задачу, определяя разными способами одни и те же явления (группа аксиом конгруэнтности у Гильберта определяет отношения конгруэнтности напрямую, аксиомы движения – через свои следствия).
Итак, будем требовать, чтобы существовали такие отражения точек, прямых и плоскостей на точки, прямые и плоскости, именуемые движениями, удовлетворяющие следующим аксиомам.
III, 1. Каждое движение Н сохраняет отношение принадлежности.
То есть, если точка А принадлежит прямой а (плоскости α), то её образ при движении Н (обозначаемый НА) принадлежит образу прямой На (соответственно образу плоскости Нα).
III, 2. Каждое движение Н сохраняет отношение порядка на прямой.
Это означает, как, наверное, уже догадался читатель, что каждому из двух направлений на прямой а можно сопоставить такое направление на прямой На, что каждый раз, когда для точек X и Y прямой а имеет место X < Y, для соответствующих им точек прямой На имеет место HX < HY.
Из этих двух аксиом следует, что каждое движение переводит полупрямую в полупрямую, полуплоскость в полуплоскость.
III, 3. Движения образуют группу.
Это значит:
а) Сопоставление Н0 каждому элементу х (точке, прямой, плоскости) его самого есть движение. Это движение называется тождественным.
б) Если движение Н1 сопоставляет произвольному элементу х элемент y, а движение Н2 сопоставляет y элемент z, то сопоставление элементу х элемента z есть движение. Оно обозначается Н2Н1 и называется произведением движений.
в) Для каждого движения Н существует движение Н-1 такое, что Н-1Н=Н0. Движение Н-1 будем называть обратным.
III, 4. Если при движении Н прямая h, как целое, и её начальная точка А остаются неподвижными, то все точки полупрямой h остаются неподвижными.
III, 5. Для каждой пары точек А и В существует движение Н, которе переставляет их местами: НА=В, НВ=А
III, 6. Для каждой пары лучей h, k (полупрямых), исходящих из одной точки, существует движение Н, их переставляющее: Нh=k, Hk=h.
III, 7. Пусть α и β – любые плоскости, а и b – прямые в этих плоскостях, А и В – точки на прямых а и b. Тогда существует движение, которое переводит точку А в В, заданную полупрямую прямой а, определяемую точкой А, - в заданную полупрямую прямой b, определяемую точкой В, заданную полуплоскость плоскости α, определяемую прямой а, – в заданную полуплоскость плоскости β, определяемую прямой b.
Теорема 10. Пусть α – плоскость, и а – принадлежащая ей прямая. Тогда если движение Н переводит каждую из полуплоскостей плоскости α, определяемых прямой а, в себя и оставляет неподвижными точки прямой а, то оно является тождественным.
Действительно, тождественное движение Н0 обладает указанными в теореме свойствами Н, а следовательно, по аксиоме III, 7 совпадает с ним.
Определим теперь понятие конгруэнтности. Фигуру F1 мы будем называть конгруэнтной фигуре F2, если существует движение Н, переводящее F1 в F2: HF1=F2. Из групповых свойств движения (аксиома III, 3) вытекают следующие свойства отношения конгруэнтности:
1. Каждая фигура F конгруэнтна сама себе.
Действительно, тождественное движение Н0 переводит F в F.
2. Если фигура F1 конгруэнтна F2, то фигура F2 конгруэнтна F1.
В самом деле, если Н – движение, переводящее фигуру F1 в F2, то движение Н-1 переводит фигуру F2 в фигуру F1.
3. Если фигура F1 конгруэнтна F2, а фигура F2 конгруэнтна фигуре F3, то фигура F1 конгруэнтна F3.
Действительно, если Н' – движение, переводящее фигуру F1 в F2, а Н'' – движение, переводящее фигуру F2 в F3, то движение Н''Н' переводит F1 в F3.
Впервые подобную систему предложил спустя десять после появления гильбертовой аксиоматики Фридрих Шур.
Спустя ещё десять лет
немецкий математик Герман Вейль (Weyl;
9.11.1885, Эльмсхорн, Шлезвиг-Гольштейн, – 8.12.1955, Цюрих) создал векторную
аксиоматику геометрии. У Вейля первоначальными являются понятия «точка» и
«вектор», а прямая и отрезок определяются с их помощью. Имеются аксиомы
сложения векторов (означающие, что векторы образуют коммутативную группу),
аксиомы умножения вектора на действительное число, аксиомы откладывания
векторов (в частности, аксиома треугольника: ![]() ),
аксиомы скалярного произведения векторов и аксиома размерности (для планиметрии
в ней утверждается: если даны три ненулевых вектора
),
аксиомы скалярного произведения векторов и аксиома размерности (для планиметрии
в ней утверждается: если даны три ненулевых вектора ![]() ,
,
![]() и
и ![]() , то какой-нибудь из них
выражается в виде комбинации двух других:
, то какой-нибудь из них
выражается в виде комбинации двух других: ![]() ).
При заданных точке А и ненулевом векторе
).
При заданных точке А и ненулевом векторе ![]() прямая
(А,
прямая
(А, ![]() ) определяется как
множество всех точек М, для которых вектор
) определяется как
множество всех точек М, для которых вектор![]() пропорционален
пропорционален
![]() , то есть найдётся такое
действительное число t,
что
, то есть найдётся такое
действительное число t,
что ![]() . Далее определяются
отрезки, углы, многоугольники, окружность и другие фигуры: например, расстояние
между А и В – как квадратный корень из скалярного квадрата вектора
. Далее определяются
отрезки, углы, многоугольники, окружность и другие фигуры: например, расстояние
между А и В – как квадратный корень из скалярного квадрата вектора ![]() , то есть
, то есть ![]() . Теорема Пифагора легко
доказывается с помощью скалярного произведения, а аксиома параллельности – с
помощью векторного определения прямой и аксиомы разномерности.
. Теорема Пифагора легко
доказывается с помощью скалярного произведения, а аксиома параллельности – с
помощью векторного определения прямой и аксиомы разномерности.
В заключение отметим, что гильбертова аксиоматика полностью уточнила не вполне совершенную систему аксиом, созданную Евклидом более двух тысяч лет тому назад. Аксиоматика Фридриха Шура и аксиоматика Германа Вейля связали геометрию с понятиями группы преобразований и векторного пространства, которые играют важнейшую роль во многих разделах современной математики, физики, экономики, химии, биологии и других областей знания.
Глава II. Неевклидовы геометрии в системе Вейля
2.1 Элементы сферической геометрии
В этом пункте рассмотрены элементы так называемой сферической геометрии - геометрии сферы евклидова пространства. Кратчайшими (геодезическими) или прямыми линиями на сфере являются большие окружности, т. е. такие окружности, плоскости которых проходят через центр данной сферы.
Так как любые два больших круга пересекаются, то в сферической геометрии не осуществляется ни постулат Евклида, ни аксиома параллельности Лобачевского. В этой геометрии не выполняется также ряд других фактов абсолютной геометрии.
Например, прямые в сферической геометрии замкнуты и на них невозможно установить понятие точки, лежащей «между» для трех точек, инцидентных прямой, так как каждую из этих точек на окружности можно считать точкой, лежащей между двумя другими. Две точки на большом круге определяют два отрезка и прямые имеют конечную длину. Таким образом, аксиомы порядка в сферической геометрии должны описывать свойства циклического расположения точек на прямой. И все же, несмотря на указанные различия в сферической геометрии имеется много свойств, аналогичных соответствующим свойствам в евклидовой геометрии и геометрии Лобачевского. Эти геометрии, включая и геометрию достаточно малых кусков сферы, в основных вопросах не противопоставляются между собою, а копируют друг друга.
Возьмем на сфере три точки А, В, С, не лежащие в одной плоскости с центром О данной сферы. Совокупность этих точек и дуг АВ, ВС и АС больших окружностей, меньших полуоборота, называется сферическим треугольником АВС. Точки А, В, С называются вершинами сферического треугольника, а дуги, АВ, ВС, АС — его сторонами. Углом А сферического треугольника АВС называется, угол между касательными, проведенными к дугам АВ и АС в точке их пересечения А. Очевидно, этот угол является линейным углом двугранного угла, образованного плоскостями больших окружностей АВ и АС. Ясно, что сферический треугольник можно получить с помощью трехгранного угла, если пересечь его сферой, центр которой будет совпадать с вершиной данного угла. В самом деле, в пересечении сферы с гранями данного трехгранного угла получим сферический треугольник.
Из школьного курса геометрии известно, что в трехгранном угле любой его плоский угол меньше суммы двух других плоских углов и больше их разности. В геометрии сферы этому предложению соответствует следующая теорема. Во всяком сферическом треугольнике каждая сторона меньше суммы двух других его сторон и больше их разности.
На основании этой теоремы, как и в обычной планиметрии, доказывается, что в сферическом треугольнике против большей стороны лежит больший угол и, обратно, против большего угла лежит большая сторона.
В этой геометрии имеются сферические двуугольники — фигуры более простые, чем сферические треугольники. Сферический двуугольник, по определению, представляет часть сферы, ограниченную двумя большими полуокружностями, пересекающимися в двух диаметрально противоположных точках.
Симметрия сферы относительно диаметральной плоскости и поворот ее вокруг диаметра на данный угол, очевидно, представляют собой примеры преобразований сферы, при которых расстояния между любыми двумя точками равно расстоянию между их образами. Приведем общее определение.
Преобразования сферы, при которых сохраняются расстояния между любыми двумя ее точками, называются движениями. Сферическая геометрия изучает свойства фигур, сохраняющиеся при любых движениях сферы.
Полярные треугольники
Всякая
плоскость ![]() ,
проходящая через центр сферы, пересекает эту сферу по большой окружности. Концы
А, А' диаметра, перпендикулярного плоскости
,
проходящая через центр сферы, пересекает эту сферу по большой окружности. Концы
А, А' диаметра, перпендикулярного плоскости ![]() , называются полюсами этой
окружности. В этом случае большая окружность называется полярой точек А и А'.
, называются полюсами этой
окружности. В этом случае большая окружность называется полярой точек А и А'.
Очевидно,
все точки поляры удалены от своего полюса на расстояние, равное ![]() R/2, где R обозначает радиус данной сферы. Ясно также, что если данная точка
удалена от двух точек большой окружности на расстояние
R/2, где R обозначает радиус данной сферы. Ясно также, что если данная точка
удалена от двух точек большой окружности на расстояние ![]() R/2, то она является полюсом этой большой окружности. Перейдем теперь к
определению полярного треугольника.
R/2, то она является полюсом этой большой окружности. Перейдем теперь к
определению полярного треугольника.
Если вершины треугольника АВС являются полюсами сторон другого сферического треугольника А1В1С1, то этот последний называется полярным треугольником по отношению к данному.
Таким
образом, радиус-вектор ![]() перпендикулярен векторам
перпендикулярен векторам ![]() и
и ![]() , т. е.
, т. е.
![]()
Аналогично будем иметь
![]()
Отсюда следует, что если треугольник А1В1С1 будет полярным к треугольнику АВС, то треугольник АВС в свою очередь будет полярным по отношению к треугольнику А1В1С1.
Таким образом, сферические треугольники АВС и А1В1С1, взаимно полярны друг другу.
Будем обозначать вершины и углы сферического треугольника большими буквами латинского алфавита А, В, С, а противоположные им стороны — соответствующими малыми буквами того же алфавита а, Ь, с. Вершины и противоположные им стороны полярного треугольника будем обозначать теми же буквами с индексами А1, В1, С1, соответственно a1, b1, c1.
Линейные элементы треугольника здесь и в дальнейших формулах входят в виде отношений к радиусу сферы, поэтому целесообразно ввести следующее понятие приведенной длины. Расстояние между двумя точками на сфере, отнесенное к ее радиусу, будем называть приведенным расстоянием.
Докажем следующее предложение о взаимно полярных треугольниках.
Теорема.
Угол одного сферического треугольника и соответствующая ему приведенная
сторона взаимно полярного треугольника дополняют друг друга до ![]() , т. е.
, т. е.
![]()
и т. д. Так как
![]() (*)
(*)
То из (*) следует, что
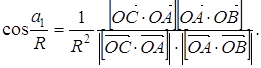
Таким образом, выводим
![]()
Аналогично доказываются остальные равенства:
![]()
Перейдем к выводу некоторых формул сферической геометрии.
Формулы прямоугольного треугольника в сферической геометрии
Перейдем
к выводу некоторых формул сферической геометрии. Пусть в евклидовом
пространстве нам дана сфера радиуса R. Возьмем на ней прямоугольный треугольник AВС со сторонами a, b, с, которые будут дугами больших кругов
соответственно ВС, СА и АВ, причем условимся считать ![]() (рис. 2).
Последнее означает, что касательные в точке С, проведенные к большим
дугам СА, СВ, перпендикулярны. Выясним связь между линейными и
угловыми элементами данного прямоугольного треугольника.
(рис. 2).
Последнее означает, что касательные в точке С, проведенные к большим
дугам СА, СВ, перпендикулярны. Выясним связь между линейными и
угловыми элементами данного прямоугольного треугольника.
Опустим из точки В перпендикуляры ВС1, и ВА1 на прямые ОС и ОА евклидова пространства. Из треугольника ОВС1, имеем
![]() (*)
(*)
Аналогично из треугольников OBA1 и BA1C1 следует, что
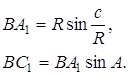 (**)
(**)
Исключая из этих трех соотношений BC1 и BA1, получим
![]() (1.1)
(1.1)
Формула (1.1) показывает, что синус приведенного катета равняется синусу приведенной гипотенузы, умноженному на синус противолежащего угла треугольника.
В предыдущем рассуждении основание С1, перпендикуляра ВС1, может совпадать с центром сферы или быть левее его на диаметре ОС. Но можно убедиться, что получаемые ниже формулы, как и формула (1.1), будут всегда справедливы. Кстати отмечу еще раз, что рассматриваются только такие сферические треугольники, которые определяются его вершинами и наименьшими дугами больших окружностей, попарно их соединяющими.
Выясним связь гипотенузы c с катетами а и b. Из треугольника ОВС1, имеем
![]() (1.2)
(1.2)
Далее из треугольника ОВА1 и ОС1А1 следует, что
![]()
Исключая из полученных трех равенств ОС1 и ОА1 будем иметь
![]() . (1.3)
. (1.3)
Эта формула выражает теорему Пифагора: косинус приведенной гипотенузы прямоугольного треугольника равняется произведению косинусов приведенных катетов. Аналогичным образом выводятся другие формулы. Например, из прямоугольного треугольника А1ВС1 следует, что
![]() (1.4)
(1.4)
Далее, так как
![]()
то из (1.2) имеем
![]() (1.5)
(1.5)
С другой стороны,
![]() (1.6)
(1.6)
Из (*, 1.4- 1.6) вытекает, что
![]() (1.7)
(1.7)
Наряду с этой формулой справедлива также парная формула
![]() (1.7')
(1.7')
Перемножая почленно последние два соотношения, получим
![]()
Отбрасывая ненулевые сомножители и применяя теорему Пифагора, окончательно будем иметь
![]() (1.8)
(1.8)
Возьмем теперь другое выражение А1С1 через соs A. Так как
![]()
то из (**) и (1.5-1.6), имеем
![]()
Отсюда следует, что
![]() (1.9)
(1.9)
Из (1.1) вытекает также, что
![]()
Последние два равенства дают
![]()
Или
![]() (1.10)
(1.10)
Доказанные формулы прямоугольного треугольника можно выписать, пользуясь так называемым правилом Непера. Чтобы сформулировать это правило, условимся располагать элементы прямоугольного треугольника а, В, с, А, b в указанном на циклическом порядке.
Для каждого из этих элементов предшествующий и последующий элементы называются прилежащими, а остальные два элемента — противолежащими. Для катета b, например, элементы a, А будут прилежащими, а элементы с, В — противолежащими. Прилежащими элементами для гипотенузы являются углы A и В, а противолежащими — катеты а и b.
Сформулируем теперь правило Непера. Косинус любого элемента сферического прямоугольного треугольника равняется произведению синусов противолежащих элементов или произведению котангенсов прилежащих элементов. Если под знаком функции стоит катет, то тригонометрическая функция меняется на смежную - синус а косинус, тангенс на котангенс и наоборот. Заметим также, что во всех формулах длины катетов и гипотенузы делятся на радиус сферы R.
Формулы косоугольного треугольника в сферической геометрии
Получим сначала теорему косинусов. Пусть АВС произвольный сферический треугольник. Опустим из вершины В высоту ВD. Применяя к треугольнику ВDС теорему Пифагора, получим
![]() ,
,
где d=AD, a=BC, b=BC, AB=c.
Перепишем предыдущее равенство, преобразуя второй множитель о формуле косинуса разности:
![]() .(1.11)
.(1.11)
Первый и
третий множители в первом члене правой части по теореме Пифагора дают ![]() . Упростим второй член в правой
части. Так как
. Упростим второй член в правой
части. Так как
![]() ,
,
то
заменяя ![]() по формуле (1.9) на
по формуле (1.9) на
![]() , получим
, получим
![]()
Таким образом, из (1.11) следует, что
![]() (1.12)
(1.12)
Эта зависимость, выражающая сторону сферического треугольника через две другие стороны в косинус противолежащего угла, называется теоремой косинусов.
Докажем теперь теорему синусов. Из прямоугольного треугольника АВD и ВDС (рис. 6) получаем
![]()
Отсюда следует, что
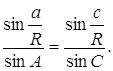
Если опустить теперь высоту из вершины А, то будем иметь
![]()
Следовательно
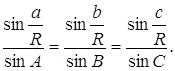 (1.13)
(1.13)
Эти зависимости сторон и синусов противолежащих углов составляют теорему синусов сферического треугольника АВС.
Вторая теорема косинусов
Предположим, что сферический треугольник А1В1С1, является полярным к данному треугольнику АВС. Применяя к нему теорему косинусов, получим
![]()
Но в силу формул (см. Полярные треугольники), имеем
![]()
Заменяя в предыдущем равенстве стороны и углы только что выписанными выражениями, получим
![]()
Или
![]() (*)
(*)
Формула и составляет содержание 2-й теоремы косинусов: Косинус угла сферического треугольника равен произведению косинусов двух других углов, взятому с обратным знаком, и сложенному с произведением синусов тех же углов на косинус приведенной противоположной стороны. Аналогичные две формулы можно получить круговой заменой линейных и угловых элементов данного треугольника АВС.
Из второй теоремы косинусов следует, что в сферической геометрии не существует неравных треугольников с соответственно равными углами. Другими словами, если углы, одного сферического треугольника равны соответствующим углам другого сферического треугольника, то такие треугольники равны.
В заключение установим лишь совпадение формул сферической геометрии для фигур с малыми линейными размерами с соответствующими формулами евклидовой геометрии.
О сферической геометрии в малом
Пусть линейные размеры а, b, с сферического треугольника малы по сравнению с радиусом сферы R. Очевидно, эти условия можно осуществить за счет малости указанных линейных размеров или за счет выбора достаточно большого значения R. Из формулы, выражающей теорему косинусов, следует
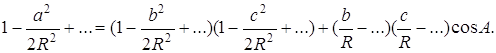
Учитывая в этом равенстве члены до второго порядка малости включительно, получим теорему косинусов евклидовой геометрии:
![]() (1.14)
(1.14)
В случае прямоугольного сферического треугольника с углом имеем cos A=0 и формула (1.12) в пределе приводит к соотношению
![]() ,
,
составляющему
теорему Пифагора в геометрии Евклида. Это равенство следует также из (1.14) при
![]() .
.
Так как при малых размерах приведенных сторон их синусы в первом приближении пропорциональны аргументам, то из (1.13) следуют две связи
![]() ,
,
выражающие теорему синусов в евклидовой геометрии.
Следовательно, формулы сферической геометрии для фигур с малыми линейными размерами по сравнению с радиусом сферы совпадают с соответствующими формулами евклидовой геометрии. Аналогичный результат получим ниже при рассмотрении формул геометрии Лобачевского.
2.2 Эллиптическая геометрия на плоскости
Были показаны простейшие факты сферической геометрии, в которой всякие две прямые пересекаются в двух диаметрально противоположных точках. Для того, чтобы освободиться от указанного недостатка и прийти к новой геометрии, в которой прямые имели бы не более одной общей точки, условимся считать всякую пару диаметрально противоположных точек сферы за одну точку. Полученную новую поверхность после такого отождествления пар точек сферы будем называть эллиптической плоскостью и обозначать символом S2.
Ясно,
что получим ту же плоскость, если будем строить фактормножество множества векторов
евклидова пространства отношению эквивалентности в которой ![]()
![]()
![]() тогда
и только тогда, когда векторы
тогда
и только тогда, когда векторы ![]() и
и
![]() непропорциональны.
непропорциональны.
Прямые эллиптической плоскости получаются из больших кругов в результате указанного отождествления пар точек и будут по-прежнему замкнутыми линиями. Но построенная плоскость S2 стала принципиально новым объектом математического исследования.
Оставаясь замкнутой поверхностью, она утратила свойство двухсторонности. Эллиптическая плоскость является односторонней поверхностью, то есть, раскрашивая какую-нибудь одну сторону этой поверхности, раскрасим ее с обеих сторон. В эллиптической геометрии отсутствует понятие точки, лежащей между двумя другими, если они инцидентны прямой, так как две точки на прямой определяют два взаимно дополнительных отрезка. В этой геометрии можно установить понятие разделения двух пар точек А, В и М, N, инцидентных прямой. Пара A, B разделяет пару М, N, если точки М, N лежат в разных отрезках, определенных на данной прямой точками А и В. Можно убедиться, что пара точек A, В разделяет пару М, N тогда и только тогда, когда двойное отношение
(АВМN) = АМ/ВМ:АN/ВN
четырех точек А, В, М, N отрицательно.
Разумеется, эллиптическую плоскость можно представить себе также в виде полусферы, у которой диаметрально противоположные точки экватора считаются за одну точку. Объекты новой модели находятся в определенных сопоставлениях с объектами известной модели на сфере. Благодаря этому без обращения к аксиомам выводим, что эти две модели реализуют одну и ту же геометрию.
Проектирование
из центра О евклидова пространства на плоскость, касательную к сфере в
точке С, где ОС![]() , переводит
прямые эллиптической плоскости в прямые евклидовой плоскости
, переводит
прямые эллиптической плоскости в прямые евклидовой плоскости ![]() . Если к точкам касательной
плоскости присоединить несобственные точки, то построенное центральное
проектирование будет взаимно однозначным отображением всех точек эллиптической
плоскости на все точки расширенной евклидовой (проективной) плоскости. Не будем
выписывать систему аксиом эллиптической геометрии и заметим лишь, что ее можно
получить из аксиом проективной геометрии и аксиом конгруентности.
. Если к точкам касательной
плоскости присоединить несобственные точки, то построенное центральное
проектирование будет взаимно однозначным отображением всех точек эллиптической
плоскости на все точки расширенной евклидовой (проективной) плоскости. Не будем
выписывать систему аксиом эллиптической геометрии и заметим лишь, что ее можно
получить из аксиом проективной геометрии и аксиом конгруентности.
Все понятия плоскости S2 переводятся по отображению в некоторые понятия двухмерной проективной геометрии. Сопоставление соответствующих геометрических образов полученной проективной модели характеризуется следующей таблицей:
| «точка» | точка проективной плоскости |
| «прямая» | прямая проективной плоскости |
| «равенство отрезков» | равенство прообразов отрезков |
Большое достоинство проективной модели состоит в том, что точки и прямые в ней изображаются привычными для нас образами. Однако, при изучении свойств конгруентных фигур сферическая модель становится более удобной.
Заметим также, что прямые и плоскости связки О евклидова пространства определяют новую модель плоскости S2, соответствующие геометрические образы которой представляются следующей таблицей:
|
S2 |
Связка прямых и плоскостей в Е3 |
| «точка» | Плоскость связки |
| «разделение двух пар точек» | Разделение двух пар прямых одного и того же пучка прямых |
| «расстояние между двумя точками» | Величина, пропорциональная углу, между двумя прямыми связки |
Реализация эллиптической плоскости в виде сферы, у которой диаметрально противоположные точки отождествлены, позволяет на этой плоскости ввести координаты (х, у, z), связанные соотношением
x2+y2+z2=R2;
где R называется радиусом кривизны, а обратная величина квадрата радиуса — кривизной. В этих координатах расстояние а между двумя точками А (х1, у1, z1) и В(х2, у2, z2 ) определяется по формуле
![]() . (2.1)
. (2.1)
Отношение
расстояния между точками к радиусу кривизны называется приведенным расстоянием.
Две точки плоскости S2
называются полярными, если соответствующие этим точкам прямые трехмерного
евклидова пространства ортогональны. Другими словами, полярные точки
характеризуются тем, что приведенное расстояние между ними равняется ![]() . Отрезок
прямой, ограниченный полярно сопряженными точками, называется полупрямой. Прямая
состоит из двух полупрямых и имеет длину, равную
. Отрезок
прямой, ограниченный полярно сопряженными точками, называется полупрямой. Прямая
состоит из двух полупрямых и имеет длину, равную ![]() . Очевидно, геометрическое место
точек, полярных данной точке А (х1, у1, z1), образует прямую
. Очевидно, геометрическое место
точек, полярных данной точке А (х1, у1, z1), образует прямую
![]() (2.1')
(2.1')
Эта прямая называется полярой точки A, а точка А - полюсом прямой (2.1').
Прямые, перпендикулярные прямой, пересекаются в ее полюсе. Обратно, всякая прямая, проходящая через полюс данной прямой, будет перпендикулярной к этой прямой. Отсюда следует, что через каждую точку плоскости, отличную от полюса данной прямой, можно провести единственный перпендикуляр к этой прямой. Эти свойства непосредственно вытекают из определения полюсов и поляр.
В геометрии S2 можно построить взаимно однозначное отображение между точками и прямыми, при котором каждой точке соответствует ее полярная прямая, а каждой прямой - ее полюс. Такое отображение называется полярным отображением. В эллиптической плоскости единичной кривизны полярное отображение переводит две прямые а, b в такие точки А, В, что расстояние между этими точками равняется углу между данными прямыми. Отсюда вытекает так называемый принцип двойственности в эллиптической планиметрии: если в какой-нибудь теореме эллиптической геометрии заменить слова «точка», «прямая», «расстояние» и «угол» соответственно на слова «прямая», «точка», «угол» и «расстояние», то в результате получим также справедливое предложение в этой геометрии. Примером двойственных предложений, т. е. предложений, получающихся одно из другого, указанного правила является следующее: любые две точки определяют прямую, им инцидентную; любые две прямые определяют точку, им инцидентную.
Найдем теперь расстояния между двумя бесконечно близкими точками М (х, у, z) и M’ (х + dх, у + dу, z + dz). Из формулы (2.1) следует, что
![]() . (2.2)
. (2.2)
Откуда с точностью до бесконечно малых второго порядка включительно имеем
ds=-2(xdx+ydy+zdz).
Учитывая, что координаты точки (х + dх, у + dу, z + dz) удовлетворяют равенству
(х + dх)2 +(у + dу)2+ (z + dz)2 =R2,
будем иметь
2(хdх + уdу + zdz) + dx2 + dу2 + dz2 = 0.
ds2 = dx2 + dу2 + dz2. (2.2')
Полученная формула приводит к очевидному выводу о том, что в малом геометрия эллиптической плоскости совпадает со сферической геометрией. В частности, формулы (1.12) и (1.13) выражающие соответственно теорему косинусов и синусов, справедливы и в эллиптической геометрии. Формула 2.2' показывает также, что движения эллиптической плоскости S2 представляются вращениями и отражениями евклидова пространства E3 вокруг начала координат. Указанные движения определяются ортогональными матрицами. Так называются матрицы, у которых сумма квадратов элементов каждого столбца равняется единице, а сумма произведений соответствующих элементов разных столбцов равняется нулю. Так как матрицы, отличающиеся знаками, индуцируют одно и то же движение в эллиптической плоскости, то группа движений последней связана.
Площадь треугольников в эллиптической геометрии
Пусть в
эллиптической плоскости дан треугольник AВС, обозначенной на рис. 8 номером I. Как известно, на данной плоскости
порождаются еще три треугольника с теми же вершинами. Эти треугольники
обозначены на рисунке номерами II, III, IV. Так как вcя
эллиптическая плоскость конечна и имеет площадь, равную 2![]() R2 , то площадь части плоскости,
ограниченной вертикальными углами А треугольника I, равняется
R2 , то площадь части плоскости,
ограниченной вертикальными углами А треугольника I, равняется
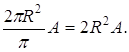
Аналогично, площадь частей эллиптической плоскости, ограниченных вертикальными углами В и С треугольника AВС, равны 2R2B, 2R2С. С другой стороны, сумма всех трех найденных площадей составляет площадь всей эллиптической плоскости с добавленной удвоенной площадью SАВС данного треугольника АВС. В результате получаем
![]() .
.
Отсюда вытекает, что
SАВС = R2(A + B + C -![]() ). (2.3)
). (2.3)
Эта формула показывает, что площадь треугольника пропорциональна его дефекту. Можно доказать, что в геометрии Лобачевского площадь треугольника АВС определяется по формуле, аналогичной (2.3),
SАВС = k2(![]() - A - B - C ),
- A - B - C ),
где k — радиус кривизны.
Окружность
Окружностью называется геометрическое место точек М(х, у, z), отстоящих от данной точки А(х1,у1,z1) на данное расстояние r. Точка A называется центром окружности, r - ее радиусом.
К
понятию окружности можно прийти другим путем, отправляясь от пучков прямых и
соответствующих точек на прямых данного пучка. Эти вспомогательные понятия
здесь вводятся так же, как в геометрии Лобачевского. Совокупность прямых,
пересекающихся в данной точке A,
называется пучком прямых первого рода. Точка А называется центром
пучка. Пучком прямых второго рода называются прямые плоскости,
перпендикулярные данной прямой а. Нетрудно убедиться, что эти пучки
двойственны друг другу. В самом деле, поляра центра пучка прямых первого рода
ортогонально пересекает все прямые пучка и рассматриваемая совокупность прямых
является пучком прямых второго рода. Обратно, прямые пучка второго рода
проходят через полюс оси пучка и составляют пучок прямых первого рода. Таким
образом, всякий пучок прямых одновременно является пучком первого и второго
рода. Предположим, что точки М и N лежат соответственно на прямых тиn данного пучка прямых. Эти точки М,
N называются соответствующими, если отрезок МN образует
равные односторонние углы с прямыми т и n. Простейшая кривая здесь определяется так же, как в
планиметрии Лобачевского. Эта кривая по определению является множеством точек,
соответствующих точке М на прямой т данного пучка. Полученная
таким образом простейшая кривая одновременно является окружностью радиуса r с центром в точке А и
эквидистантой с высотой r' = ![]() R/2 — r. Можно установить, что окружность ортогонально
рассекает прямые своего пучка.
R/2 — r. Можно установить, что окружность ортогонально
рассекает прямые своего пучка.
Из (2.1)
следует, что уравнение окружности (рис.9) с центром в точке А(х1,у1,z1) и радиусом r < ![]() R/2 приводится к виду:
R/2 приводится к виду:
![]() . (2.4)
. (2.4)
Наличие двойного знака объясняется тем, что правая часть положительна, а выражение в скобках может иметь значение разных знаков.
Заметим, что множество точек, равноудаленных от двух точек A, В, состоит из двух взаимно перпендикулярных прямых, проходящих через полюс прямой, определенной данными точками. Одна из этих прямых делит пополам один отрезок АВ, а другая - дополнительный. Отсюда вытекает существование одной и только одной окружности, описанной около заданного треугольника АВС. В частности, три точки, не принадлежащие прямой, определяют на эллиптической плоскости четыре треугольника. Таким образом, через три точки А, В, С, не лежащие на одной прямой, можно провести четыре окружности, которые на сферической модели определяются следующими тройками точек: АВС, АВС', АВ'С, А'ВС, где А', В', С' обозначают точки, диаметрально противоположные соответственно к точкам А, В, С.
Рассмотрим вкратце свойства пар окружностей в эллиптической плоскости. В сферической геометрии две окружности, как и в евклидовой плоскости, могут не пересекаться друг с другом, касаться или пересекаться в двух точках. В эллиптической геометрии свойства пар окружностей более многообразны. Чтобы убедиться в этом, предположим, что эллиптическая плоскость интерпретирована в виде сферы, у которой диаметрально противоположные точки отождествлены. В этом случае, окружность эллиптической плоскости представляется на такой сфере в виде двух окружностей, лежащих в параллельных и равноудаленных от центра сферы плоскостях. Обратно, две окружности, полученные от пересечения сферы симметрическими относительно ее центра плоскостями, изображают в эллиптической геометрии одну окружность. Сделанные замечания позволяют составить представление о новых случаях взаимных положений двух окружностей по сравнению с сферической или евклидовой планиметрией.
2.3 Геометрия Лобачевского в системе Вейля
О псевдоевклидовой планиметрии
а) В евклидовой плоскости, как известно, формула квадрата расстояния между двумя точками М(х1, х2) и N(у1, у2) в декартовой, прямоугольной системе координат представляется в виде
d(M,N)2=(y1 - x1)2+(y2 - x2)2. (3.1)
Угол ![]() между
векторами ОМ и ОN вычисляется из соотношения
между
векторами ОМ и ОN вычисляется из соотношения
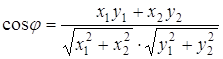 . (3.2)
. (3.2)
Первая
формула по существу выражает теорему Пифагора для прямоугольного треугольника с
катетами, равными абсолютным величинам ![]() и
гипотенузой МN.
Вторая же формула представляет собою формулу косинуса разности углов,
образованных соответственно ОМ и ON c координатным вектором
и
гипотенузой МN.
Вторая же формула представляет собою формулу косинуса разности углов,
образованных соответственно ОМ и ON c координатным вектором ![]() .
.
Теперь изменим формулы (3.1) и (3.2) и будем определять расстояние между указанными двумя точками и величины данных углов по формулам соответственно
d(M,N)=(y1 - x1)2 - (y2 - x2)2 (3.3)
 (3.4)
(3.4)
Прежние пары точек теперь будут иметь другие расстояния» а прежние углы – другие величины. Это по существу новая своеобразная двухмерная геометрия.
Чтобы подчеркнуть наличие другой метрики и не путать новые расстояния и величины углов со старыми, условимся называть координатную плоскость (x1, x2) формулами (3.3), (3.4) псевдоевклидовой плоскостью.
б) Для большей аналогии с евклидовой геометрией целесообразно ввести новое скалярное произведение векторов как произведение их длин на косинус угла между ними. Ясно, что это произведение векторов отличается от обычного скалярного произведения тех же векторов, так как длины векторов (расстояние между начальной его и конечной точками) и косинус угла понимается в смысле псевдоевклидовой геометрии.
Не будем далее перечислять следствий из формул (3.3), (3.4) и дадим аксиоматическое определение псевдоевклидовой геометрии. Делается это следующим образом.
Вместо аксиомы IV, 3 вейлевской аксиоматики, в которой говорится о том, что скалярный квадрат вектора неотрицательный, вводится другая аксиома IV, 3' о существовании ненулевых векторов первого, второго, и третьего типов, скалярные квадраты которых соответственно положительны, отрицательны и равны нулю.
Все другие аксиомы Вейля сохраняются без изменения в псевдоевклидовой геометрии. Конечно, предполагаем, что аксиомы размерности III соответствующим образом согласованы. Если речь идет о плоскости, то в аксиоме III, 1 утверждается существование двух линейно независимых векторов, а в аксиоме III, 2 утверждается, что всякие три вектора линейно зависимы.
Совокупность точек называется псевдоевклидовой плоскостью, если эти точки и их упорядоченные пары (свободные векторы) удовлетворяют аксиомам групп /--///, IV, 1, 2, 3', V. Очевидно, векторы псевдоевклидовой плоскости удовлетворяют аксиомам /--///- IV - 1, 2, 3' и образуют двухмерное псевдоевклидово векторное пространство.
В
псевдоевклидовой геометрии аффинная часть полностью
совпадает с аффинной частью евклидовой геометрии. Но в метрических вопросах
геометрии эти значительно отличаются друг
от друга, метрика пространства по существу определяется аксиомами скалярного
произведения векторов и среди них важную роль играет именно аксиома IV, 3'.
в)
Скалярное произведение двух векторов ![]() ,
,
![]() в смысле псевдоевклидовой
геометрии будем обозначать символом
в смысле псевдоевклидовой
геометрии будем обозначать символом ![]() П
П![]() . Векторы
. Векторы ![]() ,
, ![]() называются
перпендикулярными, если их скалярное произведение равно нулю.
называются
перпендикулярными, если их скалярное произведение равно нулю.
По-прежнему
число ![]() П
П![]() называется скалярным
квадратом вектора
называется скалярным
квадратом вектора ![]() ; корень
квадратный из
; корень
квадратный из ![]() П
П![]() которого называется длиной
вектора и обозначается через |
которого называется длиной
вектора и обозначается через |![]() |.Таким
образом,
|.Таким
образом,
![]() ,
,
Ясно,
что длина вектора будет положительной, чисто мнимой или нулевой, если
соответственно скалярный квадрат ![]() П
П![]() >0,
>0, ![]() П
П![]() <0 или
<0 или ![]() П
П![]() =0. Векторы
положительной и чисто мнимой длины называют также соответственно пространственными
и временными.
=0. Векторы
положительной и чисто мнимой длины называют также соответственно пространственными
и временными.
Ненулевые векторы, длины которых равны нулю, называются изотропными.
Введем
понятие прямоугольной декартовой системы координат. Прямоугольной декартовой
системой координат или просто прямоугольной системой координат псевдоевклидовой
плоскости называется такая аффинная система координат, векторы ![]() которой единичны или
мнимоединичны и взаимно перпендикулярны.
которой единичны или
мнимоединичны и взаимно перпендикулярны.
Следовательно,
один из координатных векторов псевдоевклидовой плоскости, например, ![]() будет единичным, а другой
- мнимоединичным. Таким образом, скалярное произведение координатных векторов
прямоугольной системы координат определяются равенствами
будет единичным, а другой
- мнимоединичным. Таким образом, скалярное произведение координатных векторов
прямоугольной системы координат определяются равенствами
![]() . (3.5)
. (3.5)
Очевидно, скалярное произведение двух векторов
![]()
и
квадрат длины вектора ![]() в прямоугольной системе
координат вычисляются по формулам вида
в прямоугольной системе
координат вычисляются по формулам вида
![]() (3.6)
(3.6)
![]() (3.7)
(3.7)
За
расстояние между двумя точками M(х1, х2) и N(y1, y2) определению принимается длина вектора ![]() :
:
d(M,N)2=(y1 - x1) - (y2 - x2)2.
Величиной
угла между векторами ![]() и
и
![]() называется число,
определенное по формуле
называется число,
определенное по формуле
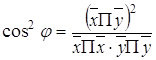 (3.8)
(3.8)
В правой
части (3.8) числитель положительный, а знаменатель при неизотропных векторах ![]() ,
, ![]() может быть
положительным и отрицательным.
может быть
положительным и отрицательным.
Если
векторы ![]() ,
, ![]() одной природы, т.
е. оба множителя в знаменателе одновременно пространственные или временные, то
одной природы, т.
е. оба множителя в знаменателе одновременно пространственные или временные, то ![]() , если же один из векторов
пространственный, а другой временный, то
, если же один из векторов
пространственный, а другой временный, то ![]() .
.
Нетрудно
далее доказать, что числитель в (3.8) не меньше знаменателя. Действительно,
если координаты векторов ![]() и
и
![]() будут
соответственно (х1, х2) и (у1, у2)
в некоторой прямоугольной системе координат, то
будут
соответственно (х1, х2) и (у1, у2)
в некоторой прямоугольной системе координат, то
![]() .
.
Следовательно,
если векторы ![]() ,
, ![]() одновременно будут
пространственными или временными, то
одновременно будут
пространственными или временными, то
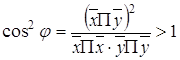 . (3.9)
. (3.9)
Полагая
в этом случае ![]() , получим
, получим
![]() . (3.10)
. (3.10)
В псевдоевклидовой плоскости существует три типа прямых в зависимости от природы ее направляющего вектора, если направляющий вектор будет пространственным, временным или изотропным, то прямая называется соответственно пространственной, временной или изотропной.
г) Перейдем теперь к определению понятия окружности.
Окружностью в псевдоевклидовой плоскости называется множество ее точек, отстоящих от данной точки, называемой центром на одно и то же расстояние r; величина r называется радиусом окружности. Выбирая прямоугольную систему координат с началом в центре окружности, убедимся, что координаты текущей точки (х1, х2) данной окружности удовлетворяют уравнению
![]() .
.
В этой геометрии существует три типа окружностей - окружности вещественного, чисто мнимого и нулевого радиусов. На рис. 13 окружности нулевого радиуса изображаются с точки зрения евклидовой геометрии биссектрисами координатных углов, окружности вещественного радиуса - гиперболами, пересекающими ось Ох1 и окружность чисто мнимого радиуса - гиперболами, пересекающими ось Ох2.
д) В заключение рассмотрим вкратце движения в псевдоевклидовой плоскости. Движение определяется как преобразование, соответствующие точки которого имеют одни и те же координаты относительно исходной и произвольно заданной прямоугольных систем координат. Как и в евклидовой геометрии доказывается, что движение является изометрией и, обратно, всякая изометрия является движением. Изометрия определяется как преобразование, сохраняющее расстояние между двумя произвольными точками. Как и в геометрии евклидовой плоскости, движения можно разделить
на
собственные движения - движения с определителем ![]() =
1 и несобственные - движения с определителем
=
1 и несобственные - движения с определителем ![]() =
- 1. Но теперь каждую из этих совокупностей в свою очередь можно разделить на
две совокупности. Чтобы убедиться в этом, отметим предварительно следующие два
замечания.
=
- 1. Но теперь каждую из этих совокупностей в свою очередь можно разделить на
две совокупности. Чтобы убедиться в этом, отметим предварительно следующие два
замечания.
Во-первых, ясно, что пространственные, временные и изотропные векторы при движениях остаются соответственно пространственными, временными и изотропными.
Во-вторых, при непрерывных вращениях вокруг данной точки векторы изотропного конуса отделяют в этой точке временные векторы от пространственных.
Перейдем теперь к дальнейшему разделению на части движений псевдоевклидовой плоскости. Нетрудно видеть, что в формулах
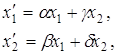 (3.11)
(3.11)
определяющих
вращение, величина ![]() не обращается в
нуль. В самом деле, предположим, что в (3.11) коэффициент
не обращается в
нуль. В самом деле, предположим, что в (3.11) коэффициент ![]() равняется нулю. В таком
случае пространственный вектор {1, 0} при вращении (3.11), перешел бы в вектор
{0,
равняется нулю. В таком
случае пространственный вектор {1, 0} при вращении (3.11), перешел бы в вектор
{0, ![]() }, который является
временным, что невозможно. Таким образом, при изменениях координатных
векторов
}, который является
временным, что невозможно. Таким образом, при изменениях координатных
векторов ![]() , вызываемых
непрерывными вращениями, коэффициент
, вызываемых
непрерывными вращениями, коэффициент ![]() будет знакопостоянным.
будет знакопостоянным.
Следовательно,
все движения делятся на четыре типа в зависимости от значения определителя
преобразования ![]() = 1 или
= 1 или ![]() = - 1 и
знака
= - 1 и
знака ![]() > 0 или
> 0 или ![]() < 0.
< 0.
Представителями этих четырех типов будут, например, движения с матрицами:
![]()
Псевдоевклидово трехмерное пространство
а) обобщим построения псевдоевклидовой плоскости на трехмерные пространства. Аксиомы псевдоевклидова трехмерного пространства совпадают с аксиомами Вейля псевдоевклидовой плоскости, за исключением аксиом размерности III. Теперь в аксиоме III-I речь идет о существовании трех линейно независимых векторов, а в аксиоме III, 2 - всякие четыре вектора линейно зависимы.
Скалярное
произведение двух векторов ![]() ,
, ![]() в псевдоевклидовом
пространстве будем обозначать, как и в случае псевдоевклидовой плоскости,
символом
в псевдоевклидовом
пространстве будем обозначать, как и в случае псевдоевклидовой плоскости,
символом ![]() . Векторы
. Векторы ![]() ,
, ![]() - перпендикулярны, если
их скалярное произведение равно нулю.
- перпендикулярны, если
их скалярное произведение равно нулю.
Число
![]() называется скалярным квадратом
вектора. Длиной вектора
называется скалярным квадратом
вектора. Длиной вектора ![]() называется
корень квадратный из скалярного квадрата этого вектора и обозначается через
называется
корень квадратный из скалярного квадрата этого вектора и обозначается через ![]() :
:
![]() .
.
Подкоренное
выражение может быть ![]() >0,
>0, ![]() <0, и
<0, и ![]() =
0. Длины векторов соответственно этим случаям будут вещественные, чисто
мнимые и нулевые. Векторы вещественной длины называются также
пространственными, векторы чисто мнимой длины — временными и векторы нулевой
длины — изотропными.
=
0. Длины векторов соответственно этим случаям будут вещественные, чисто
мнимые и нулевые. Векторы вещественной длины называются также
пространственными, векторы чисто мнимой длины — временными и векторы нулевой
длины — изотропными.
В
псевдоевклидовом пространстве вводится прямоугольная система координат. По
определению так называется аффинная система координат, векторы которой ![]() единичны или
мнимоединичны и взаимно перпендикулярны. Будем рассматривать так называемое
пространство Минковского, в котором из трех координатных векторов
прямоугольной системы координат два единичные, а третий — мнимоединичный. Будем
считать, что
единичны или
мнимоединичны и взаимно перпендикулярны. Будем рассматривать так называемое
пространство Минковского, в котором из трех координатных векторов
прямоугольной системы координат два единичные, а третий — мнимоединичный. Будем
считать, что
![]() (3.12)
(3.12)
В этой
системе координат скалярное произведение двух векторов и квадрат длины вектора ![]() , очевидно, вычисляются
по формулам вида
, очевидно, вычисляются
по формулам вида
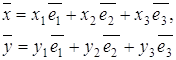
И
квадрат длины вектора ![]() , очевидно,
вычисляются по формулам вида
, очевидно,
вычисляются по формулам вида
![]() , (3.13)
, (3.13)
![]() . (3.14)
. (3.14)
За
расстояние между двумя точками М(x1, x2, x3) и N(y1, y2, y3) по определению принимается длина вектора ![]() , т. е.
, т. е.
![]() . (3.15)
. (3.15)
Величиной
угла между векторами ![]() и
и ![]() называется число, определенное по
формуле
называется число, определенное по
формуле
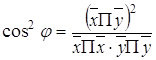 .
.
Если
векторы ![]() ,
, ![]() одной природы, т. е. оба
пространственные или временные, то
одной природы, т. е. оба
пространственные или временные, то ![]() . Более
того,
. Более
того, ![]() , если для х, у выполняется
неравенство Коши и
, если для х, у выполняется
неравенство Коши и ![]() , если
неравенство это не выполняется. Полагая в последнем случае
, если
неравенство это не выполняется. Полагая в последнем случае ![]() , получим
, получим ![]() .
.
б) В псевдоевклидовом пространстве существует три типа прямых в зависимости от природы ее направляющего вектора. Здесь существуют также три вида плоскостей в зависимости от природы ее нормального вектора.
в) Подробнее рассмотрим вопрос о сферах. Сферой псевдоевклидова пространства П3 называется множество точек этого пространства, отстоящих от данной точки А, называемой центром сферы, на одно и то же расстояние r. Величина r называется радиусом сферы.
Выбирая прямоугольную систему координат с началом в центре сферы, убедимся в том, что координаты х1, х2, х3 текущей точки сферы радиуса r удовлетворяют уравнению
![]() . (3.17')
. (3.17')
Ясно, что первые два координатных вектора прямоугольной системы здесь предполагаются единичными, а третий вектор — мнимоединичным.
В псевдоевклидовом пространстве существуют три типа сферы вещественного, чисто мнимого и нулевого радиуса.
Уравнение сферы вещественного радиуса r совпадает (3.17'), в котором величина r вещественная. Если сфера чисто мнимого радиуса r = ki, где k вещественное, то уравнение (3.17') приводится к виду
![]() (3.17)
(3.17)
Если же сфера будет нулевого радиуса, то из (3.15) следует, что
![]() . (3.18)
. (3.18)
Уравнение (3.18) в евклидовом пространстве является уравнением конуса, а предыдущие два - уравнениями гиперболоидов.
Ясно, что конус (3,18) состоит из асимптот сфер (3.17, 17'), имеющих центр в начале координат. Очевидно, асимптотический конус сферы совпадает с изотропным конусом ее центра. Из уравнения (3.15) следует также, что на сферах псевдоевклидова пространства имеются прямолинейные образующие - прямые целиком лежащие на сфере.
Очевидно,
линией пересечения сферы с плоскостью является
окружность. Если секущая плоскость проходит через начало
Координат, то радиус окружности принимает значение, равное
радиусу сферы. Получаемые таким образом окружности сферы называются большими
окружностями.
За
сферическое расстояние ![]() между двумя
точками М (
между двумя
точками М (![]() ), N (
), N (![]() ) сферы принимаем расстояние по
большой окружности, соединяющей данные точки. Очевидно, это расстояние равняется произведению радиуса сферы на значение
угла, образованного радиусами векторами
) сферы принимаем расстояние по
большой окружности, соединяющей данные точки. Очевидно, это расстояние равняется произведению радиуса сферы на значение
угла, образованного радиусами векторами ![]() ,
,![]() . Следовательно,
сферическое расстояние
. Следовательно,
сферическое расстояние ![]() определяется по
формуле
определяется по
формуле
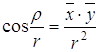 . (3.19)
. (3.19)
Если сфера чисто мнимого радиуса r = ki, то формула (3.19) приводится к виду
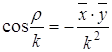 .
.
Геометрия Лобачевского
Убедимся теперь, что геометрия сферы чисто мнимого радиуса в псевдоевклидовом пространстве является Двухмерной геометрией Лобачевского. Ограничиваясь лишь одной, например, верхней полой сферы, покажем, что во множестве ее точек и больших окружностей осуществляется планиметрия Лобачевского. Для простоты эти точки можно спроектировать из центра сферы на касательную к ней плоскость в точке N. Кривую пересечения касательной плоскости с изотропным конусом будем называть абсолютом.
При проектировании точки полусферы перейдут во внутренние точки круга, ограниченного абсолютом, а большие окружности - в хорды абсолюта. Очевидно, последние являются линиями пересечения плоскостей больших окружностей с внутренностью абсолюта. Инцидентность точек и прямых понимается в обычном смысле. Ясно, что в системе точек внутренности абсолюта и его хорд аксиомы 1,1 - 3 выполняются. Аналогично аксиомы II порядка и IV непрерывности переходят в истинные предложения геометрии касательной плоскости. Что касается аксиом III группы - аксиом конгруентности, то они также переходят в истинные предложения трехмерной псевдоевклидовой геометрии. При этом считаем конгруентными те отрезки (углы), которым на сфере чисто мнимого радиуса отвечают совмещающиеся при некоторых вращениях сферы дуги больших окружностей (углы между большими окружностями).
Выясним теперь, какая выполняется аксиома параллельности: V или V’.
Предположим,
что нам дана на верхней полусфере большая окружность и не лежащая на ней точка.
В связке прямых и плоскостей, центр которой совпадает с центром сферы, этой
большой окружности и точке отвечают соответственно плоскость ![]() и прямая a связки.
и прямая a связки.
Очевидно, что через прямую а можно провести бесчисленное множество плоскостей связки, рассекающих полусферу по большим окружностям, не пересекающимися с данной большой окружностью. Таким образом в рассматриваемой модели выполняется аксиома параллельности Лобачевского. Другими словами, плоскостная геометрия Лобачевского совпадает с геометрией сферы чисто мнимого радиуса.
Эти рассуждения позволяют принять следующее общее определение n-мерных неевклидовых геометрий.
Неевклидовыми геометриями n-измерений называются геометрии, которые порождаются на n-мерных сферах, Sn вещественного или чисто мнимого радиуса в (n+1)-мерном евклидовом соответственно псевдоевклидовом пространстве. Предполагается также» что диаметрально противоположные точки этих сфер отождествлены, т. е. такие пары точек считаются за одну точку.
Из этого определения следует, что при возрастании n число типов неевклидовых пространств также растет. Неевклидовы геометрии являются геометриями простейших римановых пространств определенной и неопределенной метрики, составляющих так называемый класс пространств постоянной ненулевой кривизны. Каждое из таких n-мерных пространств допускает совокупность движений, зависящую от n(n+1)/2 параметров.
Очевидно, при n=2 получим эллиптическую плоскость и плоскость Лобачевского. Геометрия, этих плоскостей будет соответственно геометрией сферы евклидова пространства и геометрией сферы чисто мнимого радиуса в псевдоебклидовом пространстве.
Наша ближайшая задача — вывести основные формулы сферического треугольника (так называется треугольник на сфере, образованный тремя дугами больших окружностей). Эти формулы выражают основные математические соотношений в треугольниках геометрии Лобачевского.
а)
Сначала докажем так называемую теорему косинусов. Предположим, что нам дан
сферический треугольник с вершинами А(![]() ), В (
), В (![]() ), С (
), С (![]() ), углами A, В, С и противолежащими сторонами
соответственно а, b, с.
), углами A, В, С и противолежащими сторонами
соответственно а, b, с.
Очевидно, эти стороны связаны с радиус-векторами вершин сферического треугольника следующими равенствами
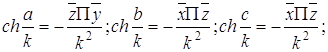 (3.21)
(3.21)
Предположим
далее, что касательная плоскость к сфере в точке С пересекает радиусы ОА и ОВ в точках ![]() и
и ![]() . Эти числовые множители
. Эти числовые множители![]() ,
,![]() радиусов векторов точек A1 и B1 определяются совсем просто, если
учесть ортогональность векторов
радиусов векторов точек A1 и B1 определяются совсем просто, если
учесть ортогональность векторов ![]() ,
, ![]() и
и ![]() ,
,
![]() Действительно,
Действительно,
![]()
т. е.
![]() .
.
Отсюда на основании (3.21) следует, что
![]() . (3.22)
. (3.22)
Повторяя
приведенные рассуждения для другой пары ![]() и
и ![]() ортогональных векторов, получим
ортогональных векторов, получим
![]() . (3.23)
. (3.23)
Найдем
теперь скалярное произведение векторов ![]() и
и ![]() .
С одной стороны, имеем
.
С одной стороны, имеем
![]() ,
,
Где
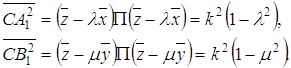
Следовательно, на основании (3.22, 3.23) имеем
![]()
Поэтому
![]() .
.
С другой стороны,
![]() .
.
Применяя затем (3.21), (3.22), (3.23), получим
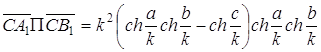 (3.25)
(3.25)
Сравнивая (3.24) и (3.25), заключаем
![]()
Или
![]() . (3.26)
. (3.26)
Формула (3.26) не зависит от нашего предположения о точках пересечения А1 и В1. Эта формула выражает теорему косинусов сферического треугольника сферы чисто мнимого радиуса: косинус гиперболической стороны сферического треугольника равен произведению косинусов гиперболических двух других сторон без произведения синусов гиперболических этих же сторон на косинус угла между ними.
б)
Переходим теперь к выводу теоремы синусов. Вычислим для этого квадрат отношения
![]() . На основании (3.26),
имеем
. На основании (3.26),
имеем
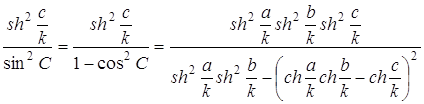 . (*)
. (*)
Видим, что числитель правой части является симметричным выражением относительно переменных а, b, с. Нетрудно убедиться, что такой же симметричностью относительно этих переменных обладает и знаменатель. В самом деле
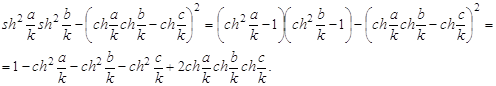 (3.27)
(3.27)
Таким
образом, квадрат искомого отношения симметричен относительно сторон а, b, с. Это означает, что заменяя обозначения
сторон а, b, с и углов А, В, С в круговом
порядке в (*) получим отношения ![]() ,
, ![]() , равные
, равные ![]() . Извлекая из этих
отношений квадратные корни, получим формулы
. Извлекая из этих
отношений квадратные корни, получим формулы
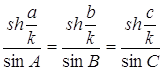 , (3.28)
, (3.28)
выражающую теорему синусов сферического треугольника в геометрии сферы чисто мнимого радиуса: синусы гиперболических сторон сферического треугольника относятся как синусы противолежащих углов.
в)
Заметим, что формулы (3.26) и (3.28) геометрии сферы чисто мнимого радиуса r = ki в псевдоевклидовом пространстве можно получить из
соответствующих формул сферического треугольника в евклидовом пространстве,
заменяя ![]() на
на ![]() ,
, ![]() на
на ![]() ,
,
![]() на
на ![]() .
.
Применяя это правило, получим вторую теорему косинусов для сферического треугольника в случае сферы мнимого радиуса:
![]() (3.29)
(3.29)
Иначе, косинус угла сферического треугольника равен произведению синусов двух других углов на косинус гиперболической стороны между этими углами без произведения косинусов двух других углов.
Отсюда следует, что если углы одного сферического треугольника равны соответствующим углам другого сферического треугольника, то такие треугольники равны.
Формулы прямоугольного треугольника
Предположим, угол С треугольника AВС является прямым. Применяя теорему косинусов (3.26), получим
![]() . (3.30)
. (3.30)
Это равенство выражает теорему Пифагора в геометрии Лобачевского: косинус гиперболической гипотенузы прямоугольного треугольника равняется произведению косинусов гиперболических катетов. Применяя формулу (3.28) будем иметь:
![]() , (3.31)
, (3.31)
![]() . (3.32)
. (3.32)
Полученные формулы можно выписать по мнемоническому правилу, аналогичному правилу Непера в сферической геометрии.
В этих
формулах связываются пять элементов прямоугольного треугольника, которые можно
рассматривать в циклическом порядке ![]() . Для
каждого элемента предшествующий и последующий элементы называются прилежащими,
а остальные два элемента - противолежащими элементами. Мнемоническое правило
формулируется следующим образом.
. Для
каждого элемента предшествующий и последующий элементы называются прилежащими,
а остальные два элемента - противолежащими элементами. Мнемоническое правило
формулируется следующим образом.
Косинус элемента прямоугольного треугольника в геометрии Лобачевского равняется произведению синусов противолежащих элементов или произведению котангенсов прилежащих элементов.
Если под знаком функции входит угол, то функция понимается в тригонометрическом смысле. Если же входит длина, то она делится на радиус кривизны и их функция понимается в гиперболическом смысле. Наконец, в случае, когда под знаком функции стоит катет, функция меняется на смежную: синус — на косинус, тангенс — на котангенс и наоборот.
Пользуясь приведенным правилом, получим для каждого элемента соответствующие выражения через прилежащие и противолежащие элементы прямоугольного треугольника:
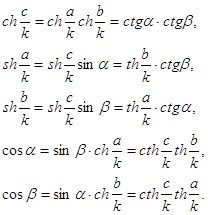 (3.33)
(3.33)
Основная формула Лобачевского
Пусть
дана на плоскости Лобачевского прямая a и точка A,
не инцидентная ей. Опустим из точки А перпендикуляр
АВ на прямую а (рис. 19). Проведем также через точку А прямую
АО, параллельную прямой а в каком-нибудь направлении. Угол ![]() , как указывали
выше, называется углом параллельности, а ответствующим отрезку АВ. Для получения
основной формул Лобачевского, связывающей угол параллельности ВАО = П(p) с отрезком p=АВ, возьмем на луче ВО какую-нибудь точку С.
Для прямоугольного треугольника AВС,
имеем
, как указывали
выше, называется углом параллельности, а ответствующим отрезку АВ. Для получения
основной формул Лобачевского, связывающей угол параллельности ВАО = П(p) с отрезком p=АВ, возьмем на луче ВО какую-нибудь точку С.
Для прямоугольного треугольника AВС,
имеем
![]()
Будем удалять теперь точку С по лучу до бесконечности, стремится при этом к 1 и в пределе, получим
![]()
Отсюда следует, что
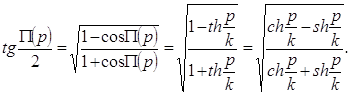
Вставляя в последнее равенство
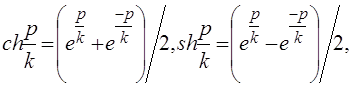
окончательно получим
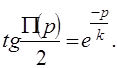
Эта формула, связывающая угол параллельности П(р) с соответствующим отрезком р, называется основной формулой Лобачевского. Из нее следует, что угол параллельности является монотонно убывающей функцией. Если отрезок параллельности р стремится к нулю, то угол параллельности стремится к прямому углу, если же р стремится к бесконечности, то угол П(р) стремиться к нулю.
Геометрия сферы пространства Лобачевского
Возьмем в трехмерном пространстве Лобачевского сферу радиуса R с центром в некоторой точке О. На этой сфере индуцируется некоторая сферическая геометрия. Получающаяся совокупность предложений называется геометрией сферы в пространстве Лобачевского. Рассмотрим в этой геометрии прямоугольный треугольник AВС, образованный из дуг АВ = с, АС = b, ВС = a больших кругов. Дуги больших кругов здесь, как и в сферической геометрии обычного пространства являются кратчайшими для достаточно близких точек на сфере. Углы между большими кругами понимаются как линейные углы двугранных углов, образованных плоскостями больших кругов. Предположим, что угол С данного треугольника прямой. Опустим далее из точки В перпендикуляры ВА1 и ВС1 на радиусы ОА и ОС соответственно. Применяя известные формулы к прямоугольному треугольнику ОВС1 (рис. 20), получим
![]()
Аналогично из треугольников ОВА1 и А1ВС1 следует, что
![]()
![]()
Исключая из этих трех соотношений ВС1 и ВA1, получим формулу
![]()
совпадающую с соответствующей формулой для прямоугольного сферического треугольника в евклидовом пространстве. Выведем теперь теорему Пифагора для прямоугольного треугольника ABС в геометрии сферы в пространстве Лобачевского. Из треугольника ОВС1 имеем
![]()
Аналогично из треугольников ОВА1 и OA1C1 соответственно следует, что
![]()
Исключая из полученных трех равенств отрезки ОС1 и OA1 выводим
![]()
Эта формула совпадает с соответствующей формулой для прямоугольного треугольника обычной сферической геометрии. Указанным способом можно убедиться, что в целом геометрия сферы пространства Лобачевского совпадает с геометрией сферы евклидова пространства.
О геометрии Лобачевского в малом
Предположим теперь, что в треугольнике линейные размеры a, b, c малы по сравнению с радиусом кривизны k пространства. Это предположение заведомо выполняется для треугольников с малыми линейными размерами или в пространстве достаточно малой кривизны 1/k2. Разлагая в степенные ряды гиперболические функции в формуле (3.26), выражающей теорему косинусов в геометрии Лобачевского, получим
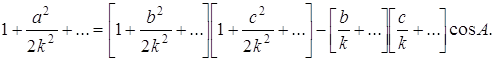
Учитывая здесь члены до второго порядка малости включительно, будем иметь
a2 = b2 + c2 – 2 bc cosA.
Эта зависимость между элементами треугольника выражает теорему косинусов в евклидовой геометрии. В случае прямоугольного треугольника cosA=0; следовательно,
a2 = b2 + c2
т. е. справедлива теорема Пифагора. Далее при наших предположениях синусы гиперболические в формуле (3.28) в первом приближении пропорциональны аргументам, поэтому
![]()
т. е. стороны треугольника пропорциональны синусам противолежащих углов. Последние три равенства позволяют утверждать, что формулы геометрии Лобачевского для фигур с малыми линейными размерами совпадают с соответствующими формулами евклидовой геометрии.
2.4 Различные модели плоскости Лобачевского. Независимость 5-го постулата Евклида от остальных аксиом Гильберта
В предыдущем параграфе познакомились с основными формулами двухмерной геометрии Лобачевского, которые в то же время были формулами геометрии сферы чисто мнимого радиуса в псевдоевклидовом пространстве.
Эта сфера, по существу, есть одна из возможных моделей плоскости Лобачевского. Другая модель - модель Бельтрами-Клейна. Она получилась из первой модели путем центрального проектирования точек сферы на какую-нибудь ее касательную плоскость. Последняя, очевидно, будет евклидовой плоскостью.
Плоскость Лобачевского в модели Бельтрами-Клейна изображается в виде внутренности круга, причем прямые изображаются хордами. Пересекающиеся прямые изображаются пересекающимися хордами. Если общая точка будет стремиться по одной из прямых к бесконечности, то параллельные прямые будут изображаться хордами, общая точка которых принадлежит абсолюту (ограничивающей внутренность круга окружности). Наконец, сверхпараллельные прямые в рассматриваемой модели изображаются хордами, которые, будучи продолжены, пересекутся в точке, принадлежащей внешней области абсолюта.
Нетрудно убедиться, что пучок прямых первого рода при Данном отображении переходит в совокупность хорд, пересекающихся в общей точке, принадлежащей внутренности абсолюта. Пучок прямых второго рода, т. е. прямых, параллельных друг другу в данном направлении, переходит в совокупность хорд, пересекающихся в некоторой точке абсолюта. Наконец, пучок прямых третьего рода отображается в совокупность хорд, пересекающихся в некоторой точке вне абсолюта. Точки абсолюта называются бесконечно удаленными точками и точки вне абсолюта - идеальными точками плоскости Лобачевского. Поэтому пучки прямых второго и третьего родов называются иногда пучками с бесконечно удаленными или соответственно идеальными центрами.
Нетрудно убедиться также, что ось пучка прямых третьего рода является полярой полюса - своего идеального центра. В самом деле, допустим, что ось пучка не является полярой идеального центра. Предположим, например, что она не проходит через точку пересечения поляры точки Р с абсолютом. Тогда на плоскости Лобачевского будет существовать прямая СС1 одновременно перпендикулярная и параллельная к прямой СВ, что невозможно.
Перенося по отображению во внутренность абсолюта основные понятия отображаемой плоскости Лобачевского, в итоге получим так называемую модель Бельтрами-Клейна.
Ясно, что к модели Бельтрами-Клейна можно прийти непосредственной проверкой аксиом Гильберта I-IV и аксиомы параллельности Лобачевского во множестве точек внутренности круга и его хорд, вводя между ними соответствующим образом основные отношения. Точками и прямыми в этой модели являются внутренние точки абсолюта и его хорды без концов. „Инцидентность" точек и прямых, а также „между" для трех точек, принадлежащих одной прямой, понимаются в обычном смысле. Два отрезка (угла) считаются конгруентными, если они будут соответствующими при некотором взаимно однозначном точечном отображении расширенной (за счет добавления несобственной прямой) евклидовой плоскости, при котором абсолют остается неизменными „прямые" переходят в „прямые".
В модели Бельтрами-Клейна длины и углы искажаются, если рисунки 23, 24 понимать в евклидовом смысле.
В рассматриваемой модели через точку А, данную вне прямой а, можно провести прямые, которые пересекают прямую а; прямые АU, АV, параллельные а и, наконец, прямые b - сверхпараллельные, располагающиеся во внутренности заштрихованных вертикальных углов. В этой модели выполняются все аксиомы Гильберта, в том числе и аксиома Лобачевского. Расстояние d(А, В) между двумя точками A, В в модели Бельтрами-Клейна выражаются при помощи проективных понятий. Если хорда АВ пересекает абсолют в точках М, N, то
![]()
где (ABMN) обозначает двойное отношение указанных четырех точек (АМ: ВМ): (АN: BN). В самом деде, предположим, что
![]() (4.1)
(4.1)
является уравнением абсолюта в однородных координатах. Кроме того, по условию нам даны точки А(аi) и В(bi). Составляя уравнение прямой АВ, получим
![]() (4.2)
(4.2)
Чтобы
найти точки пересечения М, N, прямой АВ с абсолютом, решим совместно систему уравнений (4.1) и
(4.2) относительно неизвестных ![]() . Вставляя
. Вставляя
![]() из равенства (4.2)
в уравнение (4.1), получим
из равенства (4.2)
в уравнение (4.1), получим
![]() . (4.3)
. (4.3)
Развертывая более подробно левую часть (4.3), будем иметь
![]() .
.
Так как
точка А (аi)
не принадлежит абсолюту, т. е. ![]() , то
решая квадратное уравнение
, то
решая квадратное уравнение
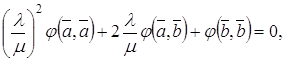
найдем
следующие значений отношения ![]() , для
искомых точек:
, для
искомых точек:
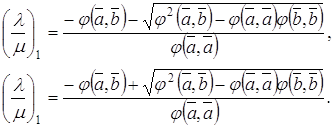
С другой
стороны, как известно, двойное отношение четырех точек А, B, М, N равно двойному отношению, составленному
из соответствующих значений параметра ![]() ,
поэтому
,
поэтому
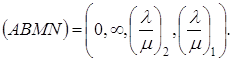
Но это равенство можно переписать в виде
![]() (4.4)
(4.4)
Вставляя
в правую часть (4.4) найденные выражения ![]() ,
,
![]() и учитывая (3.21), получим
и учитывая (3.21), получим
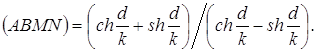
Так как по определению
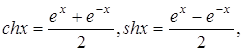
то предыдущее равенство можно переписать так:
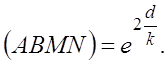
Логарифмируя это равенство, имеем окончательно
![]() (4.5)
(4.5)
Эта формула показывает, что расстояние между двумя точками А и В равняется с точностью до множителя двойному отношению данных точек А, В и точек М, N пересечения прямой АВ с абсолютом.
Угол ![]() между двумя лучами а,
b, выходящими из точки С, также выражается через
проективные понятия комплексной геометрии, Пусть т, n обозначают касательные к абсолюту,
проходящие через точку С. Заметим, что прямые m, n необходимо комплексно сопряжены. Аналогично предыдущей
формуле имеем
между двумя лучами а,
b, выходящими из точки С, также выражается через
проективные понятия комплексной геометрии, Пусть т, n обозначают касательные к абсолюту,
проходящие через точку С. Заметим, что прямые m, n необходимо комплексно сопряжены. Аналогично предыдущей
формуле имеем
![]()
Модель Бельтрами-Клейна примечательна тем, что прямые плоскости Лобачевского в ней изображаются в виде открытых отрезков прямых евклидовой плоскости. Она осуществляет геодезическое отображение плоскости Лобачевского на внутренность круга евклидовой плоскости.
Прежде чем перейти к другим моделям плоскости Лобачевского нужно сделать следующие два важных замечания. Во-первых, к модели Бельтрами-Клейна можно прийти на основе отображения плоскости Лобачевского на предельную поверхность, на которой осуществляется евклидова геометрия. Поэтому аксиомы геометрии Лобачевского здесь выполняются автоматически по отображению. Но приведенное здесь описание по отображению основных понятий позволяет в свою очередь прийти к этой модели самостоятельным образом, на основе доказательства выполнимости последовательно каждой аксиомы I — IV, V.
Во-вторых, к этой же модели Бельтрами-Клейна можно прийти, очевидно, проектированием в пространстве Минковского сферы чисто мнимого радиуса из ее центра на касательную к ней плоскость, например, в северном полюсе.
Предположим теперь, что абсолют с центром О модели Бельтрами-Клейна является большим кругом сферы. Ортогональное проектирование внутренности абсолюта на одну из полученных полусфер позволяет получить новую модель плоскости Лобачевского на полусфере. Затем стереографическое проектирование этой полусферы на исходную плоскость из полюса S, расположенного в другой полусфере, где отрезок OS перпендикулярен плоскости абсолюта, приводит к модели Пуанкаре внутри круга. Следовательно, в прежнем абсолюте прямыми теперь являются дуги окружностей, ортогонально пересекающие абсолют и диаметры абсолюта. Отношения инцидентности, лежать между и конгруентности углов имеют обычный смысл. Понятие конгруентности отрезков также соответствующим образом переносится из модели Бельтрами-Клейна.
Применяя затем дробно-линейное отображение комплексного переменного к внутренней области абсолюта, получим известную модель Пуанкаре на полуплоскости. В этой модели «точками» являются точки верхней полуплоскости, «прямыми» - полуокружности с центром на граничной прямой - абсолюте. К «прямым» причисляются также, полупрямые верхней полуплоскости, перпендикулярные к абсолютной прямой. Отношения инцидентности и лежать между понимаем в обычном смысле. Конгруентность углов в этой модели совпадает с евклидовой конгруентностью. Модель Пуанкаре представляет собою конформное отображение плоскости Лобачевского на евклидову полуплоскость.
Что касается понятия конгруентности отрезков, то оно определяется через движения или расстояние между двумя точками А и В, причем понятие расстояния между точками в последнем случае не предполагает измерения отрезков. По определению оно означает число.
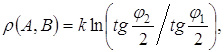 (*)
(*)
если точки A, В лежат на полуокружности или число
![]() (**)
(**)
если
точки лежат на полупрямой, перпендикулярной граничной прямой XX. В этих формулах углы ![]() ,
,
![]() и ординаты у1
, у2 имеют обычный смысл, ясный из рисунка 29,д.
и ординаты у1
, у2 имеют обычный смысл, ясный из рисунка 29,д.
Очевидно,
всегда можем предполагать, что обозначение углов символами ![]() ,
, ![]() и ординат у1,
у2 для данных точек A, В осуществлено так, что правые части в (*), (**) положительны.
Теперь нетрудно определяется конгруентность отрезков. Отрезки АВ и СD конгруентны, если расстояние между концами A, В одного отрезка равно
расстоянию между концами С, D другого
отрезка.
и ординат у1,
у2 для данных точек A, В осуществлено так, что правые части в (*), (**) положительны.
Теперь нетрудно определяется конгруентность отрезков. Отрезки АВ и СD конгруентны, если расстояние между концами A, В одного отрезка равно
расстоянию между концами С, D другого
отрезка.
Подчеркнем еще раз, что к модели Пуанкаре на полуплоскости мы пришли в результате отображения первой модели Пуанкаре во внутренности круга. Поэтому аксиомы Гильберта геометрии Лобачевского выполняются автоматически по отображению.
Приводимые здесь описания основных образов и отношений инцидентности, лежать между, конгруентности отрезков и углов позволяют прийти к этой модели Пуанкаре на полуплоскости самостоятельным образом, путем доказательства выполнимости каждой аксиомы гильбертовской аксиоматики.
В заключение остановимся на вопросе независимости 5-го постулата Евклида от остальных аксиом Гильберта. Согласно общей установке, изложенной в главе 1, достаточно построить какую-нибудь модель, на которой бы выполнялись все аксиомы Гильберта I - V за исключением аксиомы параллельности V. Аксиома эта, эквивалентная относительно аксиом I - IV утверждению 5-го постулата, состоит в следующем. Через точку А, не принадлежащую прямой а, можно провести в плоскости, определяемой этой точкой А и прямой а, не более одной прямой, не пересекающейся с данной прямой a.
Очевидно, любая модель геометрии Лобачевского, например, Бельтрами-Клейна позволяет доказать независимость аксиомы параллельности от предыдущих аксиом I - IV. Действительно, на этой модели выполняются все 19 аксиом I - IV, а аксиома V не выполняется. Отсюда заключаем, что при помощи аксиом I - IV, Гильберта невозможно доказать аксиому параллельности V. Другими словами, 5-й постулат Евклида нельзя вывести как теорему из предыдущих аксиом I - IV.
Заключение
Открытие неевклидовой геометрии, начало которому положил Лобачевский, не только сыграло огромную роль в развитии новых идей и методов в математике естествознании, но имеет и философское значение. Господствовавшее до Лобачевского мнение о незыблемости геометрии Евклида в значительной мере основывалось на учении известного немецкого философа И. Канта (1724-1804), родоначальника немецкого классического идеализма. Кант утверждал, что человек упорядочивает явления реального мира согласно априорным представлениям, а геометрические представления и идеи якобы априорны (латинское слово aprior означает – изначально, заранее), то есть, не отражают явлений действительного мира, не зависят от практики, от опыта, а являются врожденными человеческому миру, раз и навсегда зафиксированными, свойственными человеческому разуму, его духу. Поэтому, Кант считал, что Евклидова геометрия непоколебима, неизменна, и является вечной истиной. Еще до Канта геометрия Евклида считалась незыблемой, как единственно возможное учение о реальном пространстве.
Открытие неевклидовой геометрии доказало, что нельзя абсолютировать представления о пространстве, что «употребительная» (как назвал Лобачевский геометрию Евклида) геометрия не является единственно возможной, однако это не подорвало незыблемость геометрии Евклида. Итак, в основе геометрии Евклида лежат не априорные, врожденные уму понятия и аксиомы, а такие понятия, которые связаны с деятельностью человека, с человеческой практикой. Только практика может решить вопрос о том, какая геометрия вернее излагает свойства физического пространства. Открытие неевклидовой геометрии дало решающий толчок грандиозному развитию науки, способствовало и поныне способствует более глубокому пониманию окружающего нас материального мира.
Список литературы
1. Большая Советская Энциклопедия, Гл. Ред.: А. М. Прохоров, издание 3-е, Москва, Советская Энциклопедия, 1969.
2. Глейзер Г.И. История математики в школе IX – X классы. Пособие для учителей. Москва, Просвещение 1983.
3. Даан Дальмедино А., Пейффер И. Пути и лабиринты. Очерки по истории математики. Перевод с французского. М: Мир.1986г.
4. Егоров И.П. Лекции по аксиоматике Вейля и неевклидовым геометриям, Рязань, 1973Ефимов Н.В., Высшая геометрия, Наука, М.,1971.
5. Егоров И. П. «Основания геометрии», М., «Просвещение», 1984.
6. Квант №11,№12 Академик АН СССР А.Д. Александров, Интернет-издания.
7. Клайн М., Математика. Утрата определенности, Мир, М., 1984
8. Лаптев Б.Л. Н.И. Лобачевский и его геометрия. Пособие для учащихся. М. Просвещение, 1970.
9. Математика XIX века, Наука, М., 1981.
10. Неевклидовы пространства и новые проблемы физики, Белка, М., 1993.
11. Розенфельд Б.А. Неевклидовы пространства, М., Наука,1969.
12. Широков П.А. Краткий очерк основ геометрии Лобачевского, М., 1955.
13. Юшкевич А.П., История математики в России, Наука, М., 1968.
14. Яглам И.М. Принцип относительности Галилея и неевклидова геометрия. Серия Библиотека математического кружка М: 1963.
[1] Под термином «прямая пересекает отрезок» мы подразумеваем, что указанная прямая содержит некоторую внутреннюю точку этого отрезка.
1 Из этой аксиомы вытекает возможность перемещения отрезка АВ вдоль прямой, на которой он лежит (с сохранением его длины и направления). Будем говорить, что направленный отрезок получен в результате перемещения направленного отрезка , если отрезок CD конгруэнтен отрезку АВ и если либо отрезок AD лежит внутри отрезка ВС, либо отрезок ВС лежит внутри отрезка AD.