Контрольная работа: Распределение случайной величины. Эмпирические линии регрессии
Контрольная работа № 1
Задача 1
Рабочие обслуживают три станка, на которых обрабатывается однотипные детали. Вероятность изготовления бракованной детали на первом станке равна 0,2, на втором – 0,3, на третьем – 0,4. Обработанные детали складываются в один ящик. Производительность первого станка в три раза больше чем второго, а третьего – в два раза меньше чем второго. Взятая на удачу деталь оказалась бракованной. Найти вероятность того, что она изготовлена на третьем станке.
Решение:
Событие А – взятая деталь
оказалась бракованной. Деталь может быть изготовлена на первом, втором или
третьем станке, обозначим через В1, В2 и В3.
Соответственно Р(В1) = ![]() , Р(В2)
=
, Р(В2)
= ![]() , Р(В3) =
, Р(В3) = ![]() .
.
Условная вероятность того, что бракованная деталь изготовлена первым станком РВ1(А) = 0,02, аналогично РВ2(А) = 0,03 и РВ3(А) = 0,04.
По формуле полной вероятности
Р(А) = ![]()
По формуле Бейеса
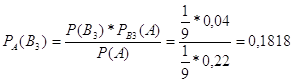
Ответ: РА(В3) = 0,1818
Задача 2
Каждая из пяти упаковок тетрадей содержит две тетради в линейку и три в клетку. Из каждой упаковки случайным образом отбираются по две тетради. Найти вероятность того, что не менее чем в трех из отобранных пяти пар тетрадей обе тетради будут в клетку.
Решение:
Вероятность взять 2 тетради в клетку из пачки
Р = ![]() .
.
Не менее трех пар из пяти отобранных должны быть – 3 пары, 4 пары, 5 пар.
Вычислим
Р5(3) + Р5(4) + Р5(5).
Pn(k) = ![]() ,
,
где р = 0,3 и q = 0,7.
Р5(3) = 0,1323
Р5(4) = 0,0284
Р5(5) = 0,0024
Искомая вероятность равна 0,1323 + 0,0284 + 0,0024 = 0,1631
Ответ: 0,1631
Задача 3
Вероятность того, что договор страховой кампании завершится выплатой по страховому случаю, равна 0,1. Страховая кампания заключила 2000 договоров. Найти вероятность того, что страховой случай наступит: а) 210 раз; б) от 190 до 250 раз включительно.
Решение:
а) Используем локальную теорему Лапласа, где k = 210, р = 0,1 и q = 0,9.
Pn(k)
= ![]() , где
, где ![]() =
=
![]()
Р2000(210) = ![]()
б) Используем интегральную теорему Лапласа, где n = 2000, k2 = 250, k1 = 190.
Pn(k1;k2) = F(x’’) - F(x’),
х’’ = ![]() .
.
х’ = ![]() .
.
F(x’’) = F(3,73) = 0,4999.
F(x’) = F(-0,75) = - 0,2764.
P2000(190;250) = 0,4999 + 0,2764 = 0,7763/
Ответ: а) Р2000(210) = 0,0224, б) Р2000(190;250) = 0,7763
Задача 4
Законное распределение независимых случайных величин Х и У имеют вид:
Х:
|
xi |
0 | 1 | 2 |
|
pi |
0,3 | ? | 0,2 |
Y:
|
yi |
1 | 2 |
|
pi |
0,4 | ? |
Найти вероятность P(X = 1), P(Y = 2).
Составить закон распределения случайной величины
Z = X*Y.
Проверить выполнение свойства математического ожидания:
M(Z) = M(X)*M(Y)
Решение:
Р(Х = 1) = 1 – (0,3 + 0,2) = 0,5
Р(Y = 2) = 1 – 0,4 = 0,6
Составим закон распределения случайной величины Z = X*Y
|
xj |
0 | 1 | 2 | |
|
yi |
pj pi |
0,3 | 0,5 | 0,2 |
| 1 | 0,4 |
0 0,12 |
1 0,2 |
2 0,08 |
| 2 | 0,6 |
0 0,18 |
20,3 |
4 0,12 |
|
zi |
0 | 1 | 2 | 4 |
|
pi |
0,3 | 0,2 | 0,38 | 0,12 |
Spi = 0,3 + 0,2 + 0,38 + 0,12 = 1
M(Z) = 0*0,3 + 1*0,2 + 2*0,38 + 4*0,12 = 1,44
M(X) = 0*0,3 + 1*0,5 + 2*0,2 = 0,9
M(Y) = 1*0,4 + 2*0,6 = 1,6
M(Z) = M(X)*M(Y) = 0,9*1,6 = 1,44.
Ответ:
|
Zi |
0 | 1 | 2 | 4 |
|
Pi |
0,3 | 0,2 | 0,38 | 0,12 |
Задача 5
Функции распределения непрерывной случайной величины Х имеет вид:
![]()
0 при х < -1,
F(x) = (х + 1)2 при -1 £ х £ 0,
1 при х > 0.
Найти математическое
ожидание этой случайной величины и вероятность того, что при каждом из трех
независимых наблюдений этой случайной величины будет выполнено условие ![]() .
.
Решение:
Найдем плотность распределения
![]()
0 при х < -1,
f(x) = F’(x) = 2(x + 1) при -1 £ х £ 0,
1 при х > 0.
М(х) = ![]()
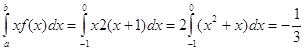
- математическое ожидание.
Р(х £ ![]() )
= Р( -1 £ х <
)
= Р( -1 £ х < ![]() )
= F(
)
= F(![]() )
– F( -1) =
)
– F( -1) = ![]()
Ответ: М(х) = ![]() и
Р(х <
и
Р(х < ![]() ) =
) = ![]()
Контрольная работа № 4
Задача 1
При выборочном опросе ста телезрителей, пользующихся услугами спутникового телевидения, получены следующие результаты распределения их по возрасту
| Возраст (лет) | Менее 20 | 20 – 30 | 30 – 40 | 40 – 50 | 50 – 60 | 60 – 70 | Более 70 | Итого |
| Количество пользователей (чел.) | 8 | 17 | 31 | 40 | 32 | 15 | 7 | 150 |
Найти:
а) Вероятность того, что средний возраст телезрителей отличается от среднего возраста, полученного по выборке, не более чем на два года (по абсолютной величине);
б) Границы, в которых с вероятностью 0,97 заключена доля телезрителей, возраст которых составляет от 30 до 50 лет;
в) Объем бесповторной выборки, при котором те же границы для доли можно гарантировать с вероятностью 0,9876; дать ответ на тот же вопрос, если никаких предварительных сведений о доле нет.
Решение:
Вычислим среднюю арифметическую и дисперсию распределения. Величина интервала k = 10 и с = 45, середина пятого интервала. Вычислим новые варианты в рабочей таблице:
| i |
[xi;xi+1] |
xi |
ui |
ni |
ui;ni |
u2i;ni |
ui +1 |
(ui + 1)ni |
| 1 | 10 – 20 | 15 | -3 | 8 | -24 | 72 | -2 | 32 |
| 2 | 20 – 30 | 25 | -2 | 17 | -34 | 68 | -1 | 17 |
| 3 | 30 – 40 | 35 | -1 | 31 | -31 | 31 | 0 | 0 |
| 4 | 40 – 50 | 45 | 0 | 40 | 0 | 0 | 1 | 40 |
| 5 | 50 – 60 | 55 | 1 | 32 | 32 | 32 | 2 | 128 |
| 6 | 60 – 70 | 65 | 2 | 15 | 30 | 60 | 3 | 135 |
| 7 | 70 – 80 | 75 | 3 | 7 | 21 | 63 | 4 | 112 |
| S | 315 | 0 | 150 | -6 | 326 | 7 | 464 |
![]()
![]()
a) Найдем среднюю квадратическую ошибку бесповторной выборки
![]()
Искомая доверительная вероятность
![]()
б) Выборочная доля зрителей от 30 до 50 лет
![]()
Средняя квадратическая ошибка бесповторной выборки для доли
![]()
Из соотношения g = Ф(t) = 0,97; t = 2,17
Предельная ошибка выборки для доли D = 2,17*0,0376 = 0,08156
Искомый доверительный интервал
0,4733 – 0,08156 £ р £ 0,4733 + 0,08156
0,3918 £ р £ 0,5549
в) Учитывая g = Ф(t) = 0,3876; t = 2,5
![]() человек.
человек.
Если о доле p = w ничего не известно, полагаем (pq)max = 0,25
![]() человек.
человек.
Ответ: а) ![]() ;
б) 0,3918 £ р £ 0,5549 ; в) 190 человек
;
б) 0,3918 £ р £ 0,5549 ; в) 190 человек
Задача 2
По данным задачи 1, используя критерий c2 – Пирсона, при уровне значимости, а = 0,5 проверить гипотезу о том, что случайная величина Х – количество телезрителей – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
Решение:
Выдвигается гипотеза Н0: случайная величина Х – количество телезрителей – распределена нормально. с параметрами а = 44,6 и d2 = 217,17.
Для расчета рi используем функцию Лапласа
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Дальнейшие расчеты покажем в таблице
| i |
[xi;xi+1] |
ni |
pi |
npi |
(ni – npi) |
|
| 1 | 10 – 20 | 8 | 0,0582 | 8,7225 | 0,522 | 0,0598 |
| 2 | 20 – 30 | 17 | 0,1183 | 17,738 | 0,5439 | 0,0307 |
| 3 | 30 – 40 | 31 | 0,2071 | 31,065 | 0,0042 | 0,0001 |
| 4 | 40 – 50 | 40 | 0,2472 | 37,073 | 8,5703 | 0,2312 |
| 5 | 50 – 60 | 32 | 0,2034 | 30,51 | 2,2201 | 0,0728 |
| 6 | 60 – 70 | 15 | 0,1099 | 16,478 | 2,183 | 0,1325 |
| 7 | 70 – 80 | 7 | 0,0517 | 7,755 | 0,57 | 0,0735 |
| S | 150 | 0,9956 | 149,34 | 0,6006 |
Фактическое значение c2 = 0,6006 Соотносим критическое значение c20,05;4 = 9,49 k = m – r – 1 = 7 – 2 – 1 = 4.
Так как c2 < c20,05;4, гипотеза Н0 согласуется с опытными данными. Выполним построение:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ: Гипотеза о выбранном теоретическом нормальном законе N (44,6; 217,17) согласуется с опытными данными.
Задача 3
Распределение 50 однотипных малых предприятий по основным фондам Х (млн., руб.) и себестоимости выпуска единицы продукции. У (тыс., руб.) представлено в таблице:
|
у х |
1,25 | 1,5 | 1,75 | 2,0 | 2,25 | Итого |
| 80 – 130 | 1 | 2 | 3 | 6 | ||
| 130 – 180 | 1 | 4 | 3 | 8 | ||
| 180 – 230 | 4 | 8 | 3 | 1 | 16 | |
| 230 – 280 | 2 | 5 | 4 | 11 | ||
| 280 – 330 | 3 | 4 | 2 | 9 | ||
| Итого: | 5 | 3 | 16 | 9 | 7 | 50 |
Необходимо:
1. Вычислить групповые средние xj и yi и построить эмпирические линии регрессии.
2. Предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:
а) найти уравнение прямых регрессий и построить их графики на одном чертеже с эмпирическими линиями регрессии;
б) вычислить коэффициент корреляции на уровне значимости, а=0,05, оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;
в) используя соответствующие уравнения регрессии, определить количество выпускаемой продукции при стоимости одной единицы продукции, равной 2,5 тыс., руб.
Решение:
1) Составим корреляционную таблицу
| х |
у xi |
1,25 | 1,5 | 1,75 | 2 | 2,25 |
ni |
уi |
| 80 – 130 | 105 | 1 | 2 | 3 | 6 | 2,0833 | ||
| 130 – 180 | 155 | 1 | 4 | 3 | 8 | 2,0625 | ||
| 180 – 230 | 205 | 4 | 8 | 3 | 1 | 16 | 1,7656 | |
| 230 – 280 | 255 | 2 | 5 | 4 | 11 | 1,5456 | ||
| 280 – 330 | 305 | 3 | 4 | 2 | 9 | 1,4722 | ||
|
nj |
5 | 13 | 16 | 9 | 7 | 50 | ||
|
xj |
285 | 255 | 220,63 | 160,56 | 140,71 |
Построим эмпирические линии регрессии

2) Предположим, что между переменными Х и Y существует линейная корреляционная зависимость;
а) Вычислим среднее значение
![]()
![]()
![]()
![]()
![]()
![]() Найдем уравнение
Найдем уравнение
ух = byx(x – x) + y,
где byx = 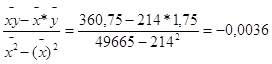
ух = - 0,0036(х – 214) + 1,75
ух = - 0,0036х + 2,5105
![]()
![]() ху - х = byx(у – у),
ху - х = byx(у – у),
где bху = 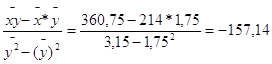
ху = - 157,14(х – 1,75) + 214
ху = - 157,14х + 489
б) Коэффициент корреляции
![]()
связь обратная и тесная;
Статистика критерия
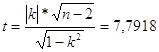
При а = 0,05 и k = 48; t0,05;48 = 2,01, так как t > t0,05;48 коэффициент значительно отличается от 0.
в) Используя ху = - 157,14у + 489
х = - 157,14*2,5 + 489 = 96,14
Ответ: а) ух = - 0,0036х + 2,5105; ху = - 157,14х + 489.
б) k = - 0,7473.
в) х = 96,14 при у = 2,5
| Шпаргалки по геометрии, алгебре, педагогике, методике математики (ИГПИ ... | |
|
Кольцом называется числ. множ. На котором выполняются три опер-ии: слож, умнож, вычит. Полем наз. Числ множ. На котором выполняются 4 операции: слож ... Кольцо полиномов от 1 неизв-го A[x]=(A[x],у, 1,+, -,*) - обл-ть целостности. => Если степень f(x)=n и степень g(x)=m => степень f(x)g(x)=n+m. Пусть А - обл-ть целостности. ni(x), fi(x), gi(x)ЄP[x], i=1,2,.k. 7. Если n(x), f(x), g(x)ЄP[x] и n(x)|f(x) и g(x)|n(x), то g(x)|f(x). 8. Мн-ны нулевой степени из Р[х] явл-ся делителями Ґf(x)ЄP[x]. 9. Мн-ны cf ... |
Раздел: Рефераты по математике Тип: реферат |
| Система математических расчетов MATLAB | |
|
ГОСУДАРСТВЕННЫЙ ИНЖЕНЕРНЫЙ УНИВЕРСИТЕТ АРМЕНИИ MATLAB УЧЕБНОЕ ПОСОБИЕ Гаспарян Олег Николаевич Д.т.н, с.н.с 2005 СОДЕРЖАНИЕ Система математических ... yi = interp1(x, y, xi, method) Find Y = f(X) - Данная панель дает возможность произвести интерполяцию или экстраполя-цию текущей подгонки. |
Раздел: Рефераты по информатике, программированию Тип: учебное пособие |
| Теория вероятностей и математическая статистика | |
|
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования "Южный ... Линейная регрессия случайных величин. будет плотностью вероятности случайной величины x. Найти функцию распределения F(x), математическое ожидание Мx. |
Раздел: Рефераты по математике Тип: учебное пособие |
| Основы программирования на языке Паскаль | |
|
Как работать с книгой Внимательно прочитайте соответствующий раздел теории (одну главу), разберите все примеры, чтобы вам все было понятно, при этом ... 1,2,4,8,11..20,24,28,30: writeln('y=',(x+1)/(sqr(x)+2)-ln(m)+2*a/b); repeat i:=u/sqrt(sqr(r)+sqr(2*pi*f*l-1/(2*pi*f*c)) |
Раздел: Рефераты по информатике, программированию Тип: учебное пособие |
| Контрольные задания для заочников по математике | |
|
Министерство образования Российской Федерации государственный технический университет МАТЕМАТИКА Методические указания и контрольные задания для ... Для случайной величины X с заданной функцией распределения F(x) требуется найти: а) плотность вероятности; б) математическое ожидание и дисперсию; в) построить графики функции ... Результаты наблюдений над двумерной случайной величиной (X,Y) приведены в табл.3. Требуется построить корреляционное поле и подобрать регрессионную зависимость Y от X ... |
Раздел: Рефераты по математике Тип: дипломная работа |