Контрольная работа: Корреляционно-регрессионный анализ
Министерство образования Российской Федерации
ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Финансово-экономический факультет
Кафедра МММЭ
КОНТРОЛЬНАЯ РАБОТА
по дисциплине "Эконометрика"
Корреляционно-регрессионный анализ
ОГУ 061700.5001.03 00
Руководитель работы
__________________ Аралбаева Г.Г.
“____”_____________ 2002г.
Исполнитель
студент гр.99 з/о ст
______________ .Чаплыгина О.Г.
“_____”____________ 2002г.
Оренбург 2002 г.
Задание
Дана выборка из генеральной совокупности по производственно-хозяйственной деятельности предприятия машиностроения (Приложение 1). Исследуется N=53 объекта по пяти признакам:
X5 –Удельный вес рабочих в составе ППП;
X7 – Коэффициент сменности оборудования;
X10 - Фондоотдача;
X14– Фондовооруженность труда;
X17 – Непроизводственные расходы;
Y1- производительность труда;
На основе полученных данных необходимо:
На основе данных необходимо:
1. По исходным данным построить классическую линейную модель множественной регрессии, оценить значимость полученного уравнения регрессии и его коэффициентов, для значимых параметров построить доверительный интервал.
2. Проанализировать матрицу парных коэффициентов корреляции на наличие мультиколинеарности, если мультиколлинеарность присутствует устранить методом пошагового отбора переменных, отобрать наиболее информативные переменные и с помощью них построить модель регрессии, оценить ее значимость.
3. Проверить построенную модель на гетероскедастичность. Построить обобщенную модель множественной регрессии (случай гетероскедастичности остатков)
4. Проверить модель на наличие автокорреляции (с помощью критерия Дарбина-Уотсона) устранить с использованием обобщенного метода наименьших квадратов на случай автокоррелированности регрессионных остатков
Введение
Пусть имеется p объясняющих переменных ![]() и
зависимая переменная У. Переменная У является случайной величиной, имеющей при
заданных значениях факторов некоторое распределение. Если случайная величина Y непрерывна, то можно считать, что ее
распределение при каждом допустимом наборе значений факторов (
и
зависимая переменная У. Переменная У является случайной величиной, имеющей при
заданных значениях факторов некоторое распределение. Если случайная величина Y непрерывна, то можно считать, что ее
распределение при каждом допустимом наборе значений факторов (![]() ) имеет условную плотность
) имеет условную плотность ![]() .
.
Обычно делается некоторое предположение относительно распределения У. Чаще всего предполагается, что условные распределения У при каждом допустимом значении факторов – нормальные. Подобное предположение позволяет получить значительно более «продвинутые» результаты.
Объясняющие переменные ![]() могут
считаться как случайными, так и детерминированными, т.е. принимающими
определенные значения.
могут
считаться как случайными, так и детерминированными, т.е. принимающими
определенные значения.
Классическая эконометрическая модель рассматривает
объясняющие переменные ![]() как
детерминированные, однако, основные результаты статистического исследования
модели остаются в значительной степени теми же, что и в случае, если считать
как
детерминированные, однако, основные результаты статистического исследования
модели остаются в значительной степени теми же, что и в случае, если считать ![]() случайными переменными.
случайными переменными.
Объясняющая часть – обозначим ее Уе – в любом случае представляет собой функцию от значений факторов – объясняющих переменных:
![]()
Таким образом, эконометрическая модель имеет вид
![]()
Наиболее естественным выбором объясненной части
случайной величины У является ее среднее значение – условное математическое
ожидание ![]() , полученное при данном
наборе значений объясняющих переменных (х1,x2,..,xp)
, полученное при данном
наборе значений объясняющих переменных (х1,x2,..,xp)
Цель работы: Исследовать корреляционно – регрессионную
зависимость между признаком у и группой аргументов ![]() .
.
Объект исследования : Производственные предприятия, занимающиеся производственной деятельностью.
Предмет исследования : корреляционная связь между признаками.
1. По исходным данным построить классическую линейную модель множественной регрессии, оценить значимость полученного уравнения регрессии и его коэффициентов, для значимых параметров построить доверительный интервал.
Построим
собственно-линейную функцию регрессии вида: ![]() ,
оценка
,
оценка ![]()
Параметры модели будем искать МНК: ![]()
Матрица Х имеет размерность 6х53, в первой строке стоят единицы.
Используя пакет STADIA оцениваем уравнение регрессии.
Получаем следующие результаты:
Таблица 1
Коэфф. a0 a1 a2 a3 a4 a5
Значение -14,9 14,4 4 0,906 0,174 0,237
Ст.ошиб. 18,4 19,8 2,91 0,992 0,188 0,216
Значим. 0,575 0,523 0,172 0,631 0,637 0,278
Источник Сум.квадр. Степ.св Средн.квадр.
Регресс. 37,2 5 7,44
Остаточн 292 47 6,22
Вся 330 52
Множеств R R^2 R^2прив Ст.ошиб. F Значим
0,33602 0,11291 0,01854 2,4942 1,2 0,325
Гипотеза 0: <Регрессионная модель неадекватна экспериментальным данным>
Оценка уравнения регрессии:
![]() =-14,9+14,4х1+4,0х2+0,906х3
+0,174х4+0,237х5
=-14,9+14,4х1+4,0х2+0,906х3
+0,174х4+0,237х5
(18,4) (19,8) (2,91) (0,992) (0.188) (0.216)
(внизу указаны стандартные ошибки каждого коэффициента регресии.)
Проверка значимости модели.
Проверим значимость построенной модели, выдвигаем гипотезу
H0: ![]() (модель
незначима)
(модель
незначима)
H1: ![]() (модель значима)
(модель значима)
Строим статистику ![]() распределена по
закону Фишера-Снедокора с числом ст. свободы n в числители и N-n-1 в знаменатели. (воспользуемся
данными таблицы 1)
распределена по
закону Фишера-Снедокора с числом ст. свободы n в числители и N-n-1 в знаменатели. (воспользуемся
данными таблицы 1)
В нашем случае F=1,2, Fкр (0,05;5;47)=2,44 т.к Fн>Fкр,то гипотеза Н0 не отвергается и модель не является значимой.
Проверка значимости коэффициентов регрессии.
Проверим на значимость коэффициенты уравнения, выдвигаем гипотезу
Н0:![]()
Н1: ![]()
Строим статистику t=![]() распределена по закону
Стьюдента с N-n-1 ст.свободы. (воспользуемся данными таблицы 1) (будем
принимать коэффициенты регрессии по абсолютному значению)
распределена по закону
Стьюдента с N-n-1 ст.свободы. (воспользуемся данными таблицы 1) (будем
принимать коэффициенты регрессии по абсолютному значению)
tb0 =- 0,810 tb3 =0,913
tb1 =0,727 tb=0,926
tb2 =1,375 tb5 =1,097
tкр(0,05;47)=2,013
tb0 ->-tкр tb3 <tкр
tb1 < tкр tb4 < tкр
tb2 < tкр tb5 < tкр
Среди всех коэффициентов значимыми являются b0, по такой модели прогноз сделать не представляется возможным, поскольку все коэффициенты регрессии при переменных не значимы.
На этом регрессионный анализ можно завершить, так как значимых переменных не обнаружено.
2. Проанализировать матрицу парных коэффициентов корреляции на наличие мультиколинеарности, если мультиколлинеарность присутствует устранить методом пошагового отбора переменных, отобрать наиболее информативные переменные и с помощью них построить модель регрессии, оценить ее значимость.
Коэффициент ковариации нормированных случайных величин называется коэффициентом корреляции, или коэффициентом парной корреляции.
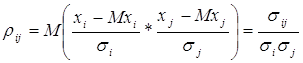 , (1)
, (1)
где ![]() - средние
квадратические отклонения случайных величин
- средние
квадратические отклонения случайных величин ![]() и
и
![]()
Для удобства расчета корреляционной матрицы, предварительно рассчитывают ковариационную матрицу .
Ковариационная матрица определяется как математическое ожидание произведения центрированного случайного вектора на этот транспонированный вектор
![]()
Матрица
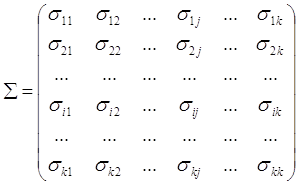 (2)
(2)
где ![]() - центральный
смешанный момент второго порядка, коэффициент ковариации i- й и j-й компонент вектора
- центральный
смешанный момент второго порядка, коэффициент ковариации i- й и j-й компонент вектора ![]() при
при
![]()
Рассмотрим матрицу исходных данных (см. Приложение 1)
1. Найдем центрированную матрицу
![]() , где Х матрица исходных данных размерности 53*6
, где Х матрица исходных данных размерности 53*6
Найдем оценку вектора ![]() ,
т.е.
,
т.е.
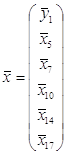
где 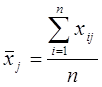 , где n = 53 – объем выборки.
, где n = 53 – объем выборки.
Используя пакет STADIA (Раздел описательная статистика), получаем вектор ![]() :
:
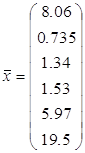
Согласно приведенной формуле ![]() рассчитываем
центрированную матрицу (Приложение 2)
рассчитываем
центрированную матрицу (Приложение 2)
2. Рассчитываем матрицу
![]()
Используя пакет STADIA (меню преобразований), получаем:
![]() =
=
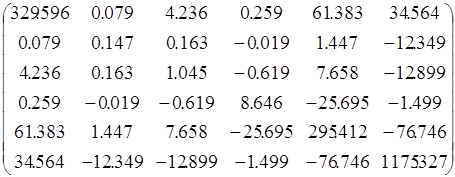
Оценку ковариационной матрицы
получим путем умножения матрицы ![]() на
множитель
на
множитель ![]()
Обозначим оценку ковариационной матрицы S, используя пакет MathCad находим:
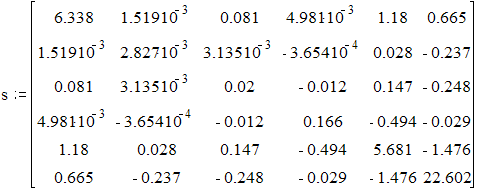
оценка ковариационной матрицы.
Для расчета ковариационной матрицы воспользуемся формулой (1) и определением ковариационной матрицы (2), получаем следующую оценку корреляционной матрицы:
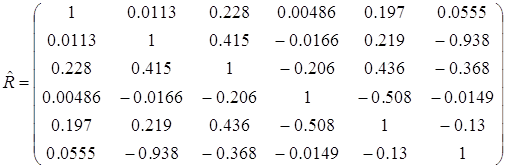
Данный расчет можно провести на прямую, используя пакет STADIA, но наша цель бала показать весь процесс расчета корреляционной матрицы. Проанализируем корреляционную матрицу.
1 – я строка и 1 – столбец это признак у , как видим наибольшая связь наблюдается между признаками х7 и х14 очень тесная (-0,938) , если анализировать парную связь между факторными признаками, то можно заметить наибольшую связь между признаком х5 и х17 (-0,938).
Устранение мультиколлинеарности с помощью метода пошаговой регрессии
Устраним мультиколлинеарность методом пошаговой регрессии,
который предполагает, что на каждом шаге мы будем включать в уравнение регрессии тот признак, который будет вызывать наибольшее приращение коэффициента детерминации.
Шаг 1
Строим
уравнения регрессии ![]()
Находим
максимальный коэффициент детерминации ![]() (где k=1)
(где k=1)
Вычисляем
нижнюю границу коэффициента детерминации 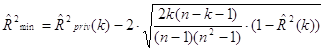 достигнет своего
максимума.
достигнет своего
максимума.
Используя пакет STADIA определяем:
| Переменная |
|
|
k |
| X17 | 0.191 | 0.7117 | 1 |
Шаг 2
Строим уравнения регрессии ![]()
Находим
максимальный коэффициент детерминации ![]() (где k=1)
(где k=1)
Вычисляем
нижнюю границу коэффициента детерминации 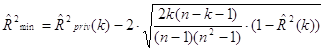 достигнет своего
максимума.
достигнет своего
максимума.
Используя пакет STADIA определяем:
| Переменная |
|
|
k |
| X7 | 0.7618 | 0.7117 | 1 |
| Х7,Х9 | 0.8118 | 0.750 | 2 |
Шаг 3
Строим уравнения регрессии ![]()
Находим
максимальный коэффициент детерминации ![]() (где k=1)
(где k=1)
Вычисляем
нижнюю границу коэффициента детерминации 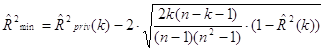 достигнет своего
максимума.
достигнет своего
максимума.
Используя пакет STADIA определяем:
| Переменная |
|
|
k |
| X7 | 0.7618 | 0.7117 | 1 |
| Х7,Х9 | 0.8118 | 0.750 | 2 |
| Х7,Х9,X3 | 0.80953 | 0.735 | 3 |
Процесс прекращаем поскольку,![]() меньше таких
коэффициентов для уравнений регрессии с двумя переменными.
меньше таких
коэффициентов для уравнений регрессии с двумя переменными.
Подробный анализ, выполненный с помощью программы “Stadia”, приведен в Приложении 1.
Граф.1
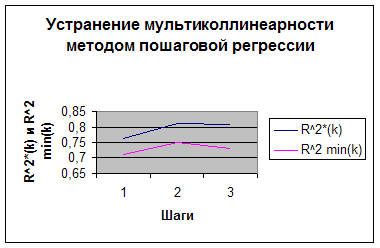
Подробные расчеты см. Приложение 1
Таким образом , из анализа исключаются все факторные признаки,
кроме Х7,X9
2. Проверить построенную модель на гетероскедастичность. Построить обобщенную модель множественной регрессии (случай гетероскедастичности остатков)
1.4 Построение и исследование новой модели регрессии.
1.4.1 Вычисление оценок коэффициентов регрессии
Регрессионная модель примет вид:
![]()
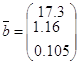
![]()
Вывод
т.к. ![]() около 1, то можно считать
, что связь тесная.
около 1, то можно считать
, что связь тесная.
Проверка значимости и построение доверительных интервалов для коэффициентов регрессии
Проверим значимость уравнения регрессии:
H0:<регрессионная модель незначима>
H1:<регрессионная модель значима>
Fвычисленное=57.1
Fкритическое (0,05;2;24)=3,40 так как Fвычисленное > Fкритическое ,
то принимается гипотеза Н1 , следовательно в уравнении коэффициенты регрессии должны быть значимыми.
Проверим значимость коэффициентов регрессии
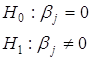 tкритическое
=2.064
tкритическое
=2.064
tвычисленное = .
![]() коэффициент значим.
коэффициент значим.
![]() коэффициент значим
коэффициент значим
.
коэффициенты
значимы, поскольку![]() > tкритическое =2.064,
> tкритическое =2.064,
![]() < tкритическое
,
< tкритическое
,
Построим доверительный интервал для коэффициентов по формуле:
![]()
где
![]() остаточная дисперсия
остаточная дисперсия
Используя пакет STADIA находим доверительный интервал для коэффициента при переменной Х7,Х9.
![]()
![]()
1.4.2 Построение доверительного интервала для результативного признака
![]() Доверительный интервал для результативного признака
будем строить , исходя из формулы:
Доверительный интервал для результативного признака
будем строить , исходя из формулы:
![]()
![]() ,
,
где
t-значение статистики Стьюдента при ![]() и
и ![]()
степенях свободы.
![]()
Построим
доверительный интервал прогноза в точке ![]() ,
используя пакет STADIA ,находим:
,
используя пакет STADIA ,находим:
![]()
2. Исследование модели на наличие гетероскедастичности
Критерий
ранговой корреляции Спирмена. По
выборочным данным строим регрессионную модель, которую оцениваем с помощью МНК.
Вычисляем регрессионные остатки: еi=уi-ýi.
Данные объясняющих переменных и остатки ранжируют, после чего исследуют
зависимость между хi и εi. Для этого выдвигаем гипотезу Нo:
нет зависимости между объясняющей переменной и регрессионными остатками ( она
равносильна гипотезе о том, что нет явления гетероскедастичности), Нı:
есть зависимость, т.е. явление гетероскедастичности наблюдается. Для проверки
гипотезы строится статистика, распределенная нормально с математическим
ожиданием равным нулю и дисперсией равной 1: t=![]() Rх.е ,
Rх.е ,
где
Rx,e=1-6*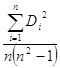 -коэффициент ранговой корреляции Спирмена, где Di2= rang xi- rang ei .
-коэффициент ранговой корреляции Спирмена, где Di2= rang xi- rang ei .
На заданном уровне значимости α=0.05 по таблице нормального распределения находим tкр
Если tн>t, то нулевую гипотезу отвергаем, значит есть явления гетероскеластичности, в противном случае явление гетероскедастичности наблюдаем. В случае наличия гетероскедастичности, используя ОМНК оценим
регрессию,
взяв в качестве матрицы Ω=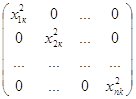
Проверим наличие гетероскедастичности по переменной Х7
|
|
|
|
rang xi |
rang ei |
Di |
Di2 |
|
21.3 69.2 77.9 17.1 18.4 37.9 72.2 27.5 58.2 46.2 74 43.5 18.8 59.5 52.2 65.1 60.2 2.63 84 19.8 78.7 62 104 69.3 78.9 15.1 51.5 |
84.98 30.58 38.42 60.34 60.22 60.79 29.82 70.57 34.51 64.73 36.63 32.84 62.64 34.07 39.27 28.46 30.27 69.04 25.42 53.13 28.00 38.79 32.04 38.58 18.51 57.62 20.80 |
-0.917 2.18 0.808 -5 -7.52 -17.5 7.55 -10.2 11.5 -21.7 2.23 0.909 -7.49 19.7 4.75 -10.3 11.9 10.8 -4.14 -8.63 -6.32 -13.4 -3.89 -5.4 -1.42 19.6 32 |
2,5 19,5 24 4,5 2,5 8,5 18 8,5 14 11 21 10 7 12,5 12,5 16 19,5 4,5 26 6 22 16 27 23 25 1 16 |
15 18 16 11 7 2 21 5 23 1 19 17 8 26 20 4 24 22 12 6 9 3 13 10 14 25 27 |
-15 -18 8 -11 -7 -2 -3 -5 -9 10 2 -7 -1 -26 -20 12 -24 -22 14 0 13 13 14 13 11 -24 -11 |
225 324 64 121 49 4 9 25 81 100 4 49 1 676 400 144 576 484 196 0 169 169 196 169 121 576 121 |
Приведем график зависимости
регрессионных остатков 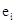 от
изменения признака Х7.
от
изменения признака Х7.
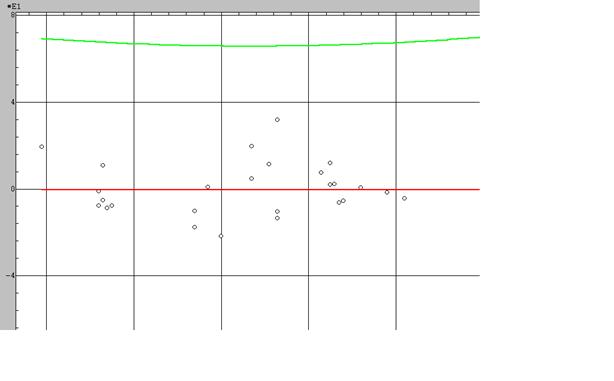
По оси ординат (У) отражено значение остатков , по оси абсцисс (х) значение признака. Как видно визуально гетероскедастичность отсутствует.
![]()
![]()
![]()
![]()
rang xi
rang ei
Di
Di2
21.3
69.2
77.9
17.1
18.4
37.9
72.2
27.5
58.2
46.2
74
43.5
18.8
59.5
52.2
65.1
60.2
2.63
84
19.8
78.7
62
104
69.3
78.9
15.1
51.5
84.98
30.58
38.42
60.34
60.22
60.79
29.82
70.57
34.51
64.73
36.63
32.84
62.64
34.07
39.27
28.46
30.27
69.04
25.42
53.13
28.00
38.79
32.04
38.58
18.51
57.62
20.80
-0.917
2.18
0.808
-5
-7.52
-17.5
7.55
-10.2
11.5
-21.7
2.23
0.909
-7.49
19.7
4.75
-10.3
11.9
10.8
-4.14
-8.63
-6.32
-13.4
-3.89
-5.4
-1.42
19.6
32
21
10
5
25
22,5
20
2,5
26
11
15
4
16
24
6,5
13
2,5
18
27
6,5
22,5
1
8
14
12
9
17
19
15
18
16
11
7
2
21
5
23
1
19
17
8
26
20
4
24
22
12
6
9
3
13
10
14
25
27
6
-8
-11
14
-7
18
-21
21
-12
14
-15
-1
16
-26
-7
-4
-6
5
-12
-6
-8
5
1
2
-5
-8
-8
36
64
121
196
49
324
441
441
144
196
225
1
256
676
49
16
36
25
144
36
64
25
1
4
25
64
64
Приведем график зависимости
регрессионных остатков 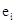 от
изменения признака Х9.
от
изменения признака Х9.
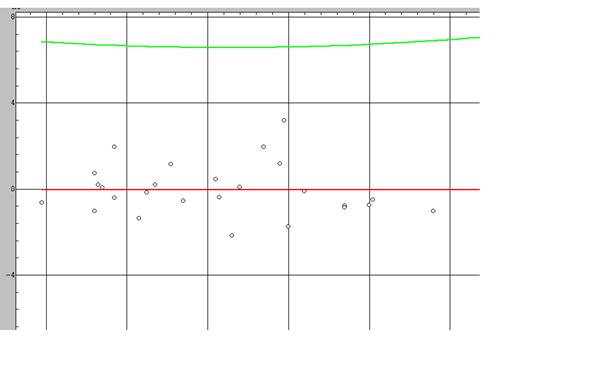
По оси ординат (У) отражено значение остатков , по оси абсцисс (х) значение признака. Как видно визуально гетероскедастичность отсутствует.
Если явление гетероскедастичности наблюдается, то оценки, полученные с помощью МНК, являются смещенными и состоятельными. В этом случае следует использовать ОМНК для построения коэффициентов регрессии: bомнк=(ΧТΩˉ¹X)ˉ¹X ТΩˉ¹Y, где Ω - диагональная матрица, которую необходимо оценить. Тогда оценка регрессии будет иметь вид:Ŷ=Xbомнк. Проверка на значимость уравнения регрессии осуществляется с помощью статистики , распределенной по закону Фишера -Снедокера.
FН= 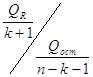 , где QR=(Xb)ТΩ-1(Хb)
, Qост=(У-Хb)ТΩ-1(У-Хb)
, где QR=(Xb)ТΩ-1(Хb)
, Qост=(У-Хb)ТΩ-1(У-Хb)
Проверка на значимость коэффициентов регрессии осуществляется с помощью статистики, распределенной по закону Стьюдента.
tн=![]() , где Sbj=Ŝ [ ( XТΩ-1Х)-1] jj
, где Sbj=Ŝ [ ( XТΩ-1Х)-1] jj![]() , Ŝ=
, Ŝ=![]()
Поскольку гетероскедастичности нет ,то нет необходимости применения ОМНК.
4. Исследование модели на наличие автокорреляции.
На практике можно провести примеры, когда построенная регрессионная модель оказывается значимой, дисперсии оценок этой модели малы, но модель оказывается неадекватной описываемому процессу. Причина этого может быть в наличии явления автокорреляции - это явление, заключающееся в том, что значения случайной составляющей в любом наблюдении зависит от его значений во всех других наблюдениях. Если в этом случае проанализировать поведение остатков, то зачастую можно выявить следующие тенденции:
● значения регрессионных остатков в соседних точках оказываются одного знака. В данном случае имеет место положительная автокорреляция.
● значения регрессионных остатков в соседних точках оказываются разного знака (по закономерности ). В этом случае имеет место отрицательная автокорреляция остатков.
Явление автокорреляции по поведению остатков можно выявить, если достаточна частота наблюдений. Автокорреляция выявляется с помощью статистики Дарбина- Уотсона:
d=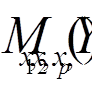
Если наличие автокорреляции отсутствует, то значение статистики должно быть
близкой к двум. При наличии положительной автокорреляции величина d
близка к нулю (меньше двух); при отрицательной автокорреляции она близка к
значению 4. Вычисляют верхнюю ![]() и нижнюю
и нижнюю![]() границы для критического
значения статистики. Возможны три ситуации:
границы для критического
значения статистики. Возможны три ситуации:
1)
Если d<d![]() , то делаем вывод о наличии автокорреляции;
, то делаем вывод о наличии автокорреляции;
2)
Если d>d![]() , то нет автокорреляции;
, то нет автокорреляции;
3)
Если d![]()
![]() <d<d
<d<d![]() , то в этом случае мы не можем ни принять ни отклонить
нулевую гипотезу и анализ осуществляется с помощью нового критерия: d’=4-d.
, то в этом случае мы не можем ни принять ни отклонить
нулевую гипотезу и анализ осуществляется с помощью нового критерия: d’=4-d.
В
случае наличия автокорреляции ее необходимо устранить, т.к построенные оценки
коэффициентов регрессии будут смещенными и состоятельными. В литературе большое
внимание уделяется зависимости первого порядка между регрессионными остатками: ![]() =
=![]() +
+![]() , где
, где ![]() <1;
<1; ![]() -случайные величины,
обладающие свойствоми: М
-случайные величины,
обладающие свойствоми: М![]() =0; D
=0; D![]() =
=![]() , cov[
, cov[![]() ,
,![]() ] =0 при i
] =0 при i![]() j т.е. относительно
j т.е. относительно ![]() мы
имеем линейную регрессионную гомоскедастичную модель. Наша цель- построить
ковариационную матрицу вектора регрессионных остатков, найти ее оценку и
построить модель ОМНК. Исследуем случайные величины
мы
имеем линейную регрессионную гомоскедастичную модель. Наша цель- построить
ковариационную матрицу вектора регрессионных остатков, найти ее оценку и
построить модель ОМНК. Исследуем случайные величины ![]() :
:
![]() М
М![]() =
= ![]()
![]() М
М![]() =0
=0
![]() D
D![]() =
=![]()
![]() , т.е. дисперсия регрессионных остатков постоянная величина.
, т.е. дисперсия регрессионных остатков постоянная величина.
![]()
![]() =
=![]()
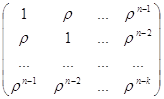
Таким образом, указали вид ковариационной матрицы вектора регрессионных
остатков. Для оценки коэффициентов регрессии ОМНК необходимо построить матрицу.
Используя вид ![]() можно указать
можно указать ![]() .
.
![]()
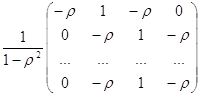
На практике величина ![]() неизвестна.
Рассмотрим способом оценивания с помощью метода Кокрейна-Оркатта, который
представляет собой итерационный подход, включающий следующие этапы:
неизвестна.
Рассмотрим способом оценивания с помощью метода Кокрейна-Оркатта, который
представляет собой итерационный подход, включающий следующие этапы:
1.
Оценивается регрессия МНК: У=Х![]()
![]() ;
;
2.
Вычисляются остатки e![]() ;
;
3.
Оценивается регрессионная
зависимость е![]() от е
от е![]() : е
: е![]() =
=![]() , коэффициент при е
, коэффициент при е![]() представляет оценку
представляет оценку ![]()
![]() ,
,
4.
Строится ![]() . Используя эту матрицу оцениваем регрессионную зависимость У от Х
ОМНК.
. Используя эту матрицу оцениваем регрессионную зависимость У от Х
ОМНК.
5.
Повторно вычисляют е![]() процесс возвращается к
пункту 3.
процесс возвращается к
пункту 3.
Процесс
заканчивается, когда значения ![]() на
последнем и предпоследнем этапах будут примерно одинаковыми.
на
последнем и предпоследнем этапах будут примерно одинаковыми.
Таким образом указан один из способов построения матрицы ![]() , в случае зависимости
регрессионных остатков первого порядка. Используя матрицу
, в случае зависимости
регрессионных остатков первого порядка. Используя матрицу ![]() можно построить вектор
оценок коэффициентов регрессии ОМНК, проверить на значимость уравнение
регрессии, построить доверительные интервалы по вышеописанным формулам
можно построить вектор
оценок коэффициентов регрессии ОМНК, проверить на значимость уравнение
регрессии, построить доверительные интервалы по вышеописанным формулам
Проверим наличие автокорреляции в модели. Составим расчетную таблицу:
|
|
|
X5 |
X7 |
X10 |
X14 |
X17 |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
9.26 9.38 12.11 10.81 9.35 9.87 8.17 9.12 5.88 6.30 6.22 5.49 6.50 6.61 4.32 7.37 7.02 8.25 8.15 8.72 6.64 8.10 5.52 9.37 13.17 6.67 6.68 6.22 10.02 8.16 6.78 6.48 10.44 7.65 8.77 7.00 11.06 9.02 13.28 9.27 6.70 6.69 9.42 7.24 5.39 5.61 5.59 6.57 6.54 4.23 5.22 18.00 11.03 |
0.78 0.75 0.68 0.70 0.62 0.76 0.73 0.71 0.69 0.73 0.68 0.74 0.66 0.72 0.68 0.77 0.78 0.78 0.81 0.79 0.77 0.78 0.72 0.79 0.77 0.80 0.71 0.79 0.76 0.78 0.62 0.75 0.71 0.74 0.65 0.66 0.84 0.74 0.75 0.75 0.79 0.72 0.70 0.66 0.69 0.71 0.73 0.65 0.82 0.80 0.83 0.70 0.74 |
1.37 1.49 1.44 1.42 1.35 1.39 1.16 1.27 1.16 1.25 1.13 1.10 1.15 1.23 1.39 1.38 1.35 1.42 1.37 1.41 1.35 1.48 1.24 1.40 1.45 1.40 1.28 1.33 1.22 1.28 1.47 1.27 1.51 1.46 1.27 1.43 1.50 1.35 1.41 1.47 1.35 1.40 1.20 1.15 1.09 1.26 1.36 1.15 1.87 1.17 1.61 1.34 1.22 |
1.45 1.30 1.37 1.65 1.91 1.68 1.94 1.89 1.94 2.06 1.96 1.02 1.85 0.88 0.62 1.09 1.60 1.53 1.40 2.22 1.32 1.48 0.68 2.30 1.37 1.51 1.43 1.82 2.62 1.75 1.54 2.25 1.07 1.44 1.40 1.31 1.12 1.16 0.88 1.07 1.24 1.49 2.03 1.84 1.22 1.72 1.75 1.46 1.60 1.47 1.38 1.41 1.39 |
6.40 7.80 9.76 7.90 5.35 9.90 4.50 4.88 3.46 3.60 3.56 5.65 4.28 8.85 8.52 7.19 4.82 5.46 6.20 4.25 5.38 5.88 9.27 4.36 10.31 4.69 4.16 3.13 4.02 5.23 2.74 3.10 10.44 5.65 6.67 5.91 11.99 8.30 1.63 8.94 5.82 4.80 5.01 4.12 5.10 3.49 4.19 5.01 11.44 7.67 4.66 4.30 6.62 |
47750 50391 43149 41089 14257 22661 52509 14903 25587 16821 19459 12973 50907 6920 5736 26705 20068 11487 32029 18946 28025 20968 11049 45893 99400 20719 36813 33956 17016 34873 11237 17306 39250 19074 18452 17500 7888 58947 94697 29626 11688 21955 12243 20193 20122 7612 27404 39648 43799 6235 11524 17309 22225 |
![]()
- - А.М. Дубров и др. , Многомерные статистические методы М.: Финансы и статистика, 1998 г. – с.320 – 323.
Приложение 2.
Центрированная матрица
Y1 цен
X5 цен
X7 цен
X10 цен
X14 цен
X17 цен
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
424344454647484950515253
1,2
1,32
4,05
2,75
1,29
1,81
0,11
1,06
-2,18
-1,76
-1,84
-2,57
-1,56
-1,45
-3,74
-0,69
-1,04
0,19
0,09
0,66
-1,42
0,04
-2,54
1,31
5,11
-1,39
-1,38
-1,84
1,96
0,1
-1,28
-1,58
2,38
-0,41
0,71
-1,06
3
0,96
5,22
1,21
-1,36
-1,37
1,36
-0,82
-2,67
-2,45
-2,47
-1,49
-1,52
-3,83
-2,84
9,94
2,97
0,045
0,015
-0,055
-0,035
-0,115
0,025
-0,005
-0,025
-0,045
-0,005
-0,055
0,005
-0,075
-0,015
-0,055
0,035
0,045
0,045
0,075
0,055
0,035
0,045
-0,015
0,055
0,035
0,065
-0,025
0,055
0,025
0,045
-0,115
0,015
-0,025
0,005
-0,085
-0,075
0,105
0,005
0,015
0,015
0,055
-0,015
-0,035
-0,075
-0,045
-0,025
-0,005
-0,085
0,085
0,065
0,095
-0,035
0,005
0,03
0,15
0,1
0,08
0,01
0,05
-0,18
-0,07
-0,18
-0,09
-0,21
-0,24
-0,19
-0,11
0,05
0,04
0,01
0,08
0,03
0,07
0,01
0,14
-0,1
0,06
0,11
0,06
-0,06
-0,01
-0,12
-0,06
0,13
-0,07
0,17
0,12
-0,07
0,09
0,16
0,01
0,07
0,13
0,01
0,06
-0,14
-0,19
-0,25
-0,08
0,02
-0,19
0,53
-0,17
0,27
0
-0,12
-0,08
-0,23
-0,16
0,12
0,38
0,15
0,41
0,36
0,41
0,53
0,43
-0,51
0,32
-0,65
-0,91
-0,44
0,07
0
-0,13
0,69
-0,21
-0,05
-0,85
0,77
-0,16
-0,02
-0,1
0,29
1,09
0,22
0,01
0,72
-0,46
-0,09
-0,13
-0,22
-0,41
-0,37
-0,65
-0,46
-0,29
-0,04
0,5
0,31
-0,31
0,19
0,22
-0,07
0,07
-0,06
-0,15
-0,12
-0,14
0,43
1,83
3,79
1,93
-0,62
3,93
-1,47
-1,09
-2,51
-2,37
-2,41
-0,32
-1,69
2,88
2,55
1,22
-1,15
-0,51
0,23
-1,72
-0,59
-0,09
3,3
-1,61
4,34
-1,28
-1,81
-2,84
-1,95
-0,74
-3,23
-2,87
4,47
-0,32
0,7
-0,06
6,02
2,33
-4,34
2,97
-0,15
-1,17
-0,96
-1,85
-0,87
-2,48
-1,78
-0,96
5,47
1,7
-1,31
-1,67
0,65
-1,78
-1,11
6,96
2,87
8,63
-1,95
2,42
0,02
4,49
2,26
6,18
-1,37
6,24
1,71
3,29
-3,12
-6,29
-5,02
-6,12
-5,81
-2,84
-4,44
0,5
-3,52
-1,23
-5,08
3,26
-4,09
-5,15
-2,67
11,03
-1,52
2,59
-1,21
6,55
6,7
-2,24
-0,67
0,2
-2,63
-4,87
2,67
3,12
6,94
2,76
-0,37
-1,22
8,73
-7,11
-7,86
-10,88
0,6
-0,09
Приложение 1
Исходные данные *
Y3
X8
X10
X15
X16
X17
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
13.26
10.16
13.72
12.85
10.63
9.12
25.83
23.39
14.68
10.05
13.99
9.68
10.03
9.13
5.37
9.86
12.62
5.02
21.18
25.17
19.40
21.0
6.57
14.19
15.81
5.23
7.99
17.50
17.16
14.54
6.24
12.08
9.49
9.28
11.42
10.031
8.65
10.94
9.87
6.14
12.93
9.78
13.22
17.29
7.11
22.49
12.14
15.25
31.34
11.56
30.14
19.71
23.56
1.23
1.04
1.80
0.43
0.88
0.57
1.72
1.70
0.84
0.60
0.82
0.84
0.67
1.04
0.66
0.86
0.79
0.34
1.60
1.46
1.27
1.58
0.68
0.86
1.98
0.33
0.45
0.74
0.03
0.99
0.24
0.57
1.22
0.68
1.00
0.81
1.27
1.14
1.89
0.67
0.96
0.67
0.98
1.16
0.54
1.23
0.78
1.16
4.44
1.06
2.13
1.21
2.20
1.45
1.30
1.37
1.65
1.91
1.68
1.94
1.89
1.94
2.06
1.96
1.02
1.85
0.88
0.62
1.09
1.60
1.53
1.40
2.22
1.32
1.48
0.68
2.30
1.37
1.51
1.43
1.82
2.62
1.75
1.54
2.25
1.07
1.44
1.40
1.31
1.12
1.16
0.88
1.07
1.24
1.49
2.03
1.84
1.22
1.72
1.75
1.46
1.60
1.47
1.38
1.41
1.39
166.32
92.88
158.04
93.96
173.88
162.30
88.56
101.16
166.32
140.76
128.52
177.84
114.48
93.24
126.72
91.80
69.12
66.24
67.68
50.40
70.56
72.00
97.20
80.28
51.48
105.12
128.52
94.68
85.32
76.32
153.00
107.64
90.72
82.44
79.92
120.96
84.60
85.32
101.52
107.64
85.32
131.76
116.64
138.24
156.96
137.52
135.72
155.52
48.60
42.84
142.20
145.80
120.52
10.08
14.76
6.48
21.96
11.88
12.60
11.52
8.28
11.52
32.40
11.52
17.28
16.20
13.32
17.28
9.72
16.20
24.84
14.76
7.56
8.64
8.64
9.00
14.76
10.08
14.76
10.44
14.76
20.52
14.40
24.84
11.16
6.48
9.72
3.24
6.48
5.4
6.12
8.64
11.88
7.92
10.08
18.72
13.68
16.56
14.76
7.92
18.36
8.28
14.04
16.92
11.16
14.76
47750
50391
43149
41089
14257
22661
52509
14903
25587
16821
19459
12973
50907
6920
5736
26705
20068
11487
32029
18946
28025
20968
11049
45893
99400
20719
36813
33956
17016
34873
11237
17306
39250
19074
18452
17500
7888
58947
94697
29626
11688
21955
12243
20193
20122
7612
27404
39648
43799
6235
11524
17309
22225
![]()
- - А.М. Дубров и др. , Многомерные статистические методы М.: Финансы и статистика, 1998 г. – с.320 – 323.
Приложение 2.
Центрированная матрица
Y3 цен
X8 цен
X10 цен
X15 цен
X16 цен
X17 цен
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
-0,44
-3,54
0,02
-0,85
-3,07
-4,58
12,13
9,69
0,98
-3,65
0,29
-4,02
-3,67
-4,57
-8,33
-3,84
-1,08
-8,68
7,48
11,47
5,7
7,3
-7,13
0,49
2,11
-8,47
-5,71
3,8
3,46
0,84
-7,46
-1,62
-4,21
-4,42
-2,28
-3,669
-5,05
-2,76
-3,83
-7,56
-0,77
-3,92
-0,48
3,59
-6,59
8,79
-1,56
1,55
17,64
-2,14
16,44
6,01
9,86
0,16
-0,03
0,73
-0,64
-0,19
-0,5
0,65
0,63
-0,23
-0,47
-0,25
-0,23
-0,4
-0,03
-0,41
-0,21
-0,28
-0,73
0,53
0,39
0,2
0,51
-0,39
-0,21
0,91
-0,74
-0,62
-0,33
-1,04
-0,08
-0,83
-0,5
0,15
-0,39
-0,07
-0,26
0,2
0,07
0,82
-0,4
-0,11
-0,4
-0,09
0,09
-0,53
0,16
-0,29
0,09
3,37
-0,01
1,06
0,14
1,13
-0,08
-0,23
-0,16
0,12
0,38
0,15
0,41
0,36
0,41
0,53
0,43
-0,51
0,32
-0,65
-0,91
-0,44
0,07
0
-0,13
0,69
-0,21
-0,05
-0,85
0,77
-0,16
-0,02
-0,1
0,29
1,09
0,22
0,01
0,72
-0,46
-0,09
-0,13
-0,22
-0,41
-0,37
-0,65
-0,46
-0,29
-0,04
0,5
0,31
-0,31
0,19
0,22
-0,07
0,07
-0,06
-0,15
-0,12
-0,14
57,32
-16,12
49,04
-15,04
64,88
53,3
-20,44
-7,84
57,32
31,76
19,52
68,84
5,48
-15,76
17,72
-17,2
-39,88
-42,76
-41,32
-58,6
-38,44
-37
-11,8
-28,72
-57,52
-3,88
19,52
-14,32
-23,68
-32,68
44
-1,36
-18,28
-26,56
-29,08
11,96
-24,4
-23,68
-7,48
-1,36
-23,68
22,76
7,64
29,24
47,96
28,52
26,72
46,52
-60,4
-66,16
33,2
36,8
11,52
-2,82
1,86
-6,42
9,06
-1,02
-0,3
-1,38
-4,62
-1,38
19,5
-1,38
4,38
3,3
0,42
4,38
-3,18
3,3
11,94
1,86
-5,34
-4,26
-4,26
-3,9
1,86
-2,82
1,86
-2,46
1,86
7,62
1,5
11,94
-1,74
-6,42
-3,18
-9,66
-6,42
-7,5
-6,78
-4,26
-1,02
-4,98
-2,82
5,82
0,78
3,66
1,86
-4,98
5,46
-4,62
1,14
4,02
-1,74
1,86
-1,78
-1,11
6,96
2,87
8,63
-1,95
2,42
0,02
4,49
2,26
6,18
-1,37
6,24
1,71
3,29
-3,12
-6,29
-5,02
-6,12
-5,81
-2,84
-4,44
0,5
-3,52
-1,23
-5,08
3,26
-4,09
-5,15
-2,67
11,03
-1,52
2,59
-1,21
6,55
6,7
-2,24
-0,67
0,2
-2,63
-4,87
2,67
3,12
6,94
2,76
-0,37
-1,22
8,73
-7,11
-7,86
-10,88
0,6
-0,09
| Управление процентным риском портфеля ГКО-ОФЗ в посткризисный период | |
|
Московский государственный университет экономики, статистики и информатики На правах рукописи Мельников Роман Михайлович Управление процентным риском ... Все параметры оказались статистически значимыми, автокорреляция остатков не была обнаружена. Для того, чтобы отобрать наиболее значимые опережающие индикаторы для модели прогнозирования темпа прироста спот-ставки рынка ГКО-ОФЗ для срока один год, диссертант воспользовался ... |
Раздел: Рефераты по финансовым наукам Тип: дипломная работа |
| Эконометрические методы в сельском хозяйстве | |
|
... эконометрического изучения и анализа производственных затрат и себестоимости зерна 2. Многофакторный корреляционно-регрессионный анализ 3. Вычисление ... Задачи курсового проекта: на основе корреляционно - регрессионного анализа провести исследование влияния факторов на фактическую посевную площадь сельскохозяйственных предприятий ... В этом случае следует изменить форму связи факторных и результативного признаков, а не использовать специальные методы расчета параметров уравнения регрессии при наличии ... |
Раздел: Рефераты по экономике Тип: курсовая работа |
| Кадры в сфере услуг и их роль в системе менеджмента | |
|
СОДЕРЖАНИЕ ВВЕДЕНИЕ ГЛАВА 1 Теоретические аспекты разработки и совершенствования системы управления персоналом на предприятии 1.1 Тенденции рынка ... Для регрессионной модели, построенной для коэффициента текучести значимым (существенным) факторным показателем оказался средний стаж работников (его увеличение на 1% вызвало бы ... Мезозавр 1.1 Модель множественной линейной регрессии для переменной ВЫРАБОТКА Зависимая переменная: |
Раздел: Рефераты по менеджменту Тип: дипломная работа |
| Факторы, влияющие на уровень разводов в Российской Федерации | |
|
ФАКТОРЫ, ВЛИЯЮЩИЕ НА УРОВЕНЬ РАЗВОДОВ В РОССИЙСКОЙ ФЕДЕРАЦИИ Оглавление Введение 1. Сбор данных и отбор факторов 2. Исследование влияние каждого ... Построим модель множественной линейной регрессии: Также проверим коэффициенты линейной регрессии на значимость: , а , |
Раздел: Рефераты по государству и праву Тип: курсовая работа |
| Система математических расчетов MATLAB | |
|
ГОСУДАРСТВЕННЫЙ ИНЖЕНЕРНЫЙ УНИВЕРСИТЕТ АРМЕНИИ MATLAB УЧЕБНОЕ ПОСОБИЕ Гаспарян Олег Николаевич Д.т.н, с.н.с 2005 СОДЕРЖАНИЕ Система математических ... Матрица V*D*inv(V), которая в более сжатой форме может быть записана как V*D/V, равна, в пределах погрешностей округления, матрице А. Аналогично, inv(V)*A*V, или V\A*V, рав-на, в ... Составим сов-местную систему уравнений, сформировав матрицу регрессии X и решив уравнения отно-сительно неизвестных коэффициентов, применяя оператор \ |
Раздел: Рефераты по информатике, программированию Тип: учебное пособие |
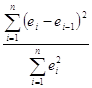 =5998.124/2736.788= 2.191
=5998.124/2736.788= 2.191