Учебное пособие: Общая теория статистики
Федеральное агентство по образованию
Министерства образования и науки Российской Федерации
Государственное образовательное учреждения высшего профессионального образования
Березниковский филиал
Пермского государственного университета
Кафедра экономики
СТАТИСТИКА
Учебно-методическое пособие
Березники, 2009 г.
Содержание
Предисловие
1. Методические рекомендации для решения задач по общей теории статистики
2. Задания к контрольной работе
Список рекомендуемой литературы
Предисловие
Изучение дисциплины «Статистика» предполагает формирование у слушателей теоретических основ и практических навыков в области познания социально-экономических явлений и процессов.
В результате изучения данной дисциплины студент должен усвоить систему обобщающих статистических показателей, овладеть методами обработки экономической информации, методологией комплексного анализа социально-экономических явлений на микро и макро уровнях.
При освоении дисциплины "Статистика" необходимо руководствоваться программами по:
1. Общей теории статистики;
2. Социально-экономической статистике.
Для более глубокого изучения студентам важнейших научно-методологических принципов статистики, приобретения практических навыков работы со статистическим материалом и методами его обработки и анализа, выработки умения правильно интерпретировать и грамотно формулировать аналитические выводы по рассчитанным статистическим показателям, необходимо выполнить контрольную работу.
Задания к контрольной работе составлены в восьми вариантах (1–4 задачи по разделу общей теории статистики, 5–8 - по социально-экономической статистике).
Выбор варианта производится в зависимости от начальной буквы фамилии слушателя.
| Начальная буква фамилии студента | Номер выполняемого варианта |
| А, И, Х, Э | первый |
| Б, Р, Ч | второй |
| В, П, Ц | третий |
| Г, О, Ф | четвертый |
| Д, Н, У | пятый |
| Е, М, С, Ш | шестой |
| Ж, Л, Т, Ю | седьмой |
| З, К, Щ, Я | восьмой |
Если в процессе выполнения контрольной работы возникнут трудности, то можно обратиться на кафедру экономики за консультацией (устной или письменной). В письменном запросе необходимо четко сформулировать непонятный вопрос и какой литературой студент при этом пользовался. При обращении на кафедру за устной консультацией необходимо показать преподавателю, что сделано по той или иной задаче и какие вопросы вызвали затруднение (непонятно изложено в литературе или в условии задачи).
При выполнении контрольной работы и ее оформлении необходимо руководствоваться следующими требованиями:
1. Контрольная работа должна быть выполнена в срок, установленный учебным планом.
2. В начале работы указывается номер выполняемого варианта.
3. Перед решением задачи должно быть полностью приведено ее условие.
4. Решение задач сопровождается описанием методологии расчета показателя или необходимыми формулами с пояснением условных обозначений в этих формулах.
Задачи, по которым будет приведена только арифметика, без пояснений и кратких выводов, или использованы не общепринятые сокращения (без пояснений), будут считаться нерешенными.
При решении задач необходимо проверять производимые расчеты, учитывая взаимосвязь вычисляемых показателей.
Расчеты относительных показателей нужно производить с точностью до 0,001, а проценты - до 0,1 (с учетом округлений).
5. Контрольная работа должна быть аккуратно оформлена, написана разборчиво (при плохом подчерке лучше отпечатать), страницы пронумерованы и иметь широкие поля для замечаний рецензента
Там, где решение задачи оформляется в табличной форме, таблицы должны быть построены и оформлены в соответствии с правилами, принятыми в статистике.
6. В конце работы приводится список использованной литературы (автор, название, место издания, издательство, год издания, глава, параграф, страница).
Студенты не получившие зачет по контрольной работе, не допускаются к экзамену.
1. Методические рекомендации для решения задач по общей тории статистики
Задача 1. Для решения этой задачи необходимо изучить темы общей теории статистики: ”Средние величины”, “Показатели вариации” и “Выборочное наблюдение”.
В условии задачи дается интервальный вариационный ряд распределения с открытыми интервалами. Чтобы определить среднее значение признака (пункт 1), нужно от интервального ряда перейти к дискретному, т.е. найти середину каждого интервала как полусумму нижней и верхней границ. При этом величина открытого интервала первой группы приравнивается к величине интервала второй группы, а величина открытого интервала последней группы - к величине интервала предпоследней группы.
Разновидностью средней являются мода и медиана (пункт 2). Эти величины также используются в качестве характеристик вариационного ряда.
Мода (Мо) – варианта, встречающаяся в ряду распределения чаще всего, т.е. варианта, которой соответствует наибольшая частота.
Для дискретного ряда распределения мода определяется наиболее просто: варианта, против которой расположена наибольшая частота, и будет модой.
В интервальном ряду наибольшая частота указывает не на модальную варианту, а на содержащий моду интервал. Вычисление моды производится по следующей формуле:
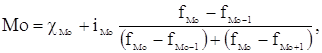
где ![]() - начало (нижняя граница)
модального интервала;
- начало (нижняя граница)
модального интервала; ![]() - величина
интервала;
- величина
интервала; ![]() - частота модального
интервала;
- частота модального
интервала; ![]() - частота интервала,
предшествующего модальному;
- частота интервала,
предшествующего модальному; ![]() -
частота интервала, следующего за модальным.
-
частота интервала, следующего за модальным.
Медиана ![]() – варианта, находящаяся
в середине ранжированного ряда распределения. Для ее определения достаточно
расположить в порядке возрастания или убывания все варианты. Серединная
варианта и будет являться медианой. Расчет медианы для интервального ряда
производится по формуле:
– варианта, находящаяся
в середине ранжированного ряда распределения. Для ее определения достаточно
расположить в порядке возрастания или убывания все варианты. Серединная
варианта и будет являться медианой. Расчет медианы для интервального ряда
производится по формуле:
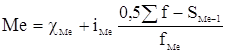
![]() –
начало (нижняя граница) медианного интервала; iMe – величина
интервала;
–
начало (нижняя граница) медианного интервала; iMe – величина
интервала; ![]() – сумма всех частот ряда;
– сумма всех частот ряда; ![]() – сумма накопленных частот
вариантов до медианного;
– сумма накопленных частот
вариантов до медианного; ![]() –частота
медианного интервала.
–частота
медианного интервала.
Для характеристики
размеров колеблемости признаков в статистике используют ряд показателей (см.
тему “ Показатели вариации”). В задаче 1 нужно исчислить дисперсию ![]() , среднее квадратическое
отклонение
, среднее квадратическое
отклонение ![]() и коэффициент вариации
и коэффициент вариации ![]() (пункт 3):
(пункт 3):
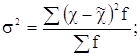
![]() ;
; 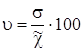
Чтобы рассчитать ошибки
выборки (![]() ) и возможные границы
генеральной средней (
) и возможные границы
генеральной средней (![]() ) и генеральной
доли признака (
) и генеральной
доли признака (![]() ) нужно изучить
тему “Выборочное наблюдение”.
) нужно изучить
тему “Выборочное наблюдение”.
Рассчитанная в пункте 1
данной задачи средняя является по условию задачи выборочной средней (![]() ). Возможная граница
генеральной средней (пункт 4) определяется по формуле:
). Возможная граница
генеральной средней (пункт 4) определяется по формуле:
![]() ,
,
где
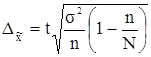
предельная ошибка выборочной средней (для бесповторного отбора).
Возможная граница генеральной доли определяется по формуле:
![]()
![]()
где w – выборочная доля (удельный вес единиц в выборке, обладающих исследуемым признаком; w = m/n)
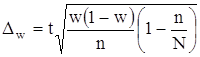
предельная ошибка выборочной доли (для бесповторного отбора).
Задача 2. Эта задача составлена на расчет и усвоение аналитических показателей динамических рядов. В условии задачи дан интервальный динамический ряд, поэтому средний уровень ряда может быть исчислен только по формуле средней арифметической простой:
![]()
т.е. средний уровень ряда равен сумме уровней ряда, деленной на их число.
В зависимости от задачи
исследования абсолютные приросты (снижения,![]() ),
темпы роста (снижения, Т) и темпы прироста (снижения,
),
темпы роста (снижения, Т) и темпы прироста (снижения, ![]() ) могут быть рассчитаны с
переменной базой сравнения (цепные) и постоянной базой сравнения (базисные).
) могут быть рассчитаны с
переменной базой сравнения (цепные) и постоянной базой сравнения (базисные).
Абсолютные приросты:
цепные
........................................![]()
базисные......................................![]()
Средний абсолютный прирост исчисляется двумя способами:
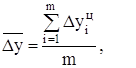
![]()
где ![]() – цепные абсолютные
приросты; m – число цепных
абсолютных приростов.
– цепные абсолютные
приросты; m – число цепных
абсолютных приростов.
Темпы роста:
цепные...........................................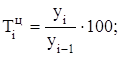
базисные..........................................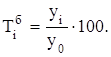
Среднегодовой темп роста исчисляется по формуле средней геометрической двумя способами:
![]()
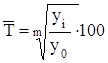
где ![]() - цепные коэффициенты
роста; m
-
число этих коэффициентов.
- цепные коэффициенты
роста; m
-
число этих коэффициентов.
Темпы прироста:
цепные...................................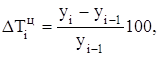
базисные..................................![]()
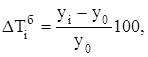
или ![]()
Среднегодовой темп прироста равен:
![]()
Абсолютное значение одного процента прироста (снижения) – это отношение абсолютного цепного прироста к соответствующему цепному темпу прироста, выраженному в процентах. Оно определяется по формуле:

Задачи 3 и 4. Составлены по теме «Индексы».
Индексом в статистике называется относительный показатель, характеризующий соотношение по времени, по сравнению с планом или в пространстве уровней социально-экономических явлений.
При построении индексов рекомендуется придерживаться следующей символики: количество единиц данного вида произведенной или реализованной продукции обозначается – q; цена единицы изделия – p; себестоимость единицы изделия – z; трудоемкость единицы изделия – t; выработка продукции на одного работающего – w; удельный расход материалов (топлива) – m и т. д. Подстрочный значок 0 означает базисный, а 1 – отчетный периоды. Индивидуальный индекс обозначается латинской буквой i, а общий – I .
В первой части задачи 3 нужно рассчитать агрегатные индексы и сделать анализ влияния факторов по системе взаимосвязанных индексов.
Например, общие индексы необходимо исчислить по формулам:
1) общий индекс затрат на производство продукции:
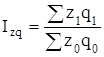 ,
,
2) общий агрегатный индекс себестоимости продукции:
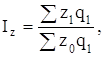
3) общий агрегатный
индекс физического объема производства продукции:![]()
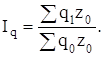
Эти индексы взаимосвязаны между собой:
![]()
Чтобы найти абсолютное изменение показателей, нужно от числителя соответствующего индекса вычесть его знаменатель. Так, абсолютный прирост (снижение) затрат на производство продукции равен:
![]() ,
,
в том числе: за счет изменения себестоимости продукции:
![]()
физического объема продукции:
![]()
Вторая часть задачи 3 составлена на расчет индекса переменного состава, индекса постоянного состава и индекса, измеряющего влияние изменения структуры на динамику среднего показателя (индекс структурных сдвигов).
Индекс переменного состава равен соотношению средних уровней изучаемого признака. Если, например, изучается динамика средней себестоимости одноименной продукции на двух и более заводах, то индекс себестоимости переменного состава исчисляется по формуле:
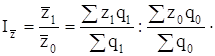
Изменение средней себестоимости единицы продукции может быть обусловлено изменением себестоимости единицы продукции на каждом заводе и изменением удельного веса производства продукции на каждом из анализируемых заводов.
Выявление влияния каждого из этих факторов на динамику средней себестоимости продукции можно осуществить при помощи расчета индекса себестоимости постоянного состава и индекса структурных сдвигов.
Индекс себестоимости постоянного (фиксированного) состава или индекс себестоимости в постоянной структуре, исчисляется по формуле:
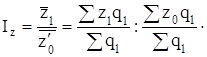
Этот индекс характеризует изменение средней себестоимости единицы продукции за счет изменения только уровней себестоимости на каждом из заводов.
Индекс структурных сдвигов рассчитывается по формуле:
![]() стр.сдв.=
стр.сдв.=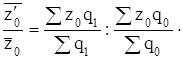
Этот индекс характеризует изменение средней себестоимости единицы продукции за счет изменения только удельного веса количества произведенной продукции на отдельных заводах.
Индекс структурных сдвигов можно исчислить, используя взаимосвязи индексов, то есть:
![]() стр..сдв
стр..сдв![]() .
.
Используя индексы
средних величин, можно найти не только относительное влияние факторов, но и
определить абсолютное изменение уровня среднего показателя в целом (![]() ) и за счет каждого из
факторов: за счет непосредственного изменения уровней осредняемого признака (
) и за счет каждого из
факторов: за счет непосредственного изменения уровней осредняемого признака (![]() ) и за счет изменения
структуры (
) и за счет изменения
структуры (![]() (стр. сдв.).).
Для этого необходимо из числителя соответствующего индекса приведенной системы
индексов вычесть его знаменатель.
(стр. сдв.).).
Для этого необходимо из числителя соответствующего индекса приведенной системы
индексов вычесть его знаменатель.
![]()
![]()
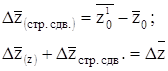
Задача 4. Составлена на расчет среднеарифметического или среднегармонического индексов. Практическое их применение зависит от исходной статистической информации. Агрегатный индекс может быть преобразован в среднеарифметический или среднегармонический индекс, при этом должно быть соблюдено тождество между индексами.
Если у исходного агрегатного индекса реальная величина в числителе, то преобразуем его в среднегармоническую форму, если же реальная величина его у исходного агрегатного индекса в знаменателе, то преобразуем его в среднеарифметическую форму. Например, индекс цен:
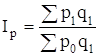
В числителе индекса реальная величина - фактический товарооборот отчетного периода. Заменив po значением из индивидуального индекса:
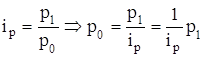 ,
, 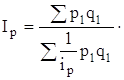
Это и есть среднегармонический индекс цен.
Агрегатный индекс физического объема товарооборота
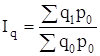 ,
,
исходя из правила, может быть будет преобразован в среднеарифметический индекс, т.е.
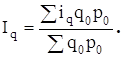
2. Задания к контрольной работе
Вариант первый (выполняют студенты, фамилии которых начинаются с букв А, И, Х, Э)
Задача 1. При выборочном обследовании 19% изделий партии готовой продукции по методу бесповторного отбора получены следующие данные о содержании влаги в образцах:
| Влажность, % | Число образцов |
| до 13 | 4 |
| 13–15 | 16 |
| 15–17 | 50 |
| 17–19 | 24 |
| 19 и выше | 6 |
| Итого: | 100 |
На основании данных выборочного обследования вычислите:
1) средний процент влажности готовой продукции;
2) моду и медиану влажности продукции;
3) дисперсию, среднее квадратическое отклонение и коэффициент вариации;
4) с вероятностью 0,954 возможные пределы ,в которых ожидается средний процент влажности всей готовой продукции;
5) с вероятностью 0,997 возможные пределы удельного веса стандартной продукции во всей готовой продукции при условии, что к нестандартной продукции относятся изделия с влажностью до 13 и свыше 19%.
Задача 2. Урожайность пшеницы в районе характеризуется следующими данными:
| Год | Средняя урожайность пшеницы, ц/га |
| 2004 | 32.0 |
| 2005 | 34.8 |
| 2006 | 36.5 |
| 2007 | 35.4 |
| 2008 | 41.8 |
Для анализа динамики средней урожайности пшеницы вычислите:
1) абсолютные приросты, темпы роста и темпы прироста по годам и к 2004 году, абсолютное содержание одного процента прироста (снижения) по годам. Полученные показатели представьте в таблице;
2) среднегодовую урожайность пшеницы за 2004–2008 гг.;
3) среднегодовые: абсолютный прирост, темп роста и темп прироста урожайности пшеницы за весь анализируемый период.
Постройте график динамики урожайности пшеницы за 2004–2008 гг. Сформулируйте выводы.
Задача 3. Динамика себестоимости и объема производства продукции характеризуется следующими данными:
| Продукция | Выработано продукции, ед. | Себестоимость единицы продукции, тыс. руб. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| Завод №1 | ||||
| КВ-45 | 1100 | 1250 | 20 | 21 |
| ПФ-50 | 2500 | 2000 | 32 | 36 |
| Завод №2 | ||||
| ПФ-50 | 4000 | 5000 | 42 | 40 |
На основании имеющихся данных вычислите:
1. Для завода №1 (по двум видам продукции вместе):
а) общий индекс затрат на производство продукции;
б) общий индекс себестоимости продукции;
в) общий индекс физического объема производства продукции.
Определите в отчетном периоде по сравнению с базисным абсолютное изменение суммы затрат на производство продукции и разложите его по факторам (за счет изменения себестоимости и объема выработанной продукции).
Покажите взаимосвязь между исчисленными индексами.
2. Для двух заводов вместе (по продукции ПФ-50):
а) индекс себестоимости переменного состава;
б) индекс себестоимости постоянного состава;
в) индекс влияния изменения структуры производства продукции на динамику средней себестоимости.
Объясните различие между полученными величинами индексов постоянного и переменного состава.
Определите общее абсолютное изменение средней себестоимости единицы продукции в отчетном периоде по сравнению с базисным и разложите его по факторам за счет непосредственного изменения уровней себестоимости и изменения структуры производства продукции.
Сделайте выводы.
Задача 4. Имеются данные о продаже фруктов на рынке:
| Фрукты | Продано на сумму, млн. руб. | Изменение количества проданных фруктов в сентябре по сравнению с августом, % | |
| август | сентябрь | ||
| Сливы | 15 | 15 | -12 |
| Груши | 30 | 32 | +10 |
| Яблоки | 55 | 50 | Без изменения |
Вычислите общие индексы:
1) выручки от продажи фруктов;
2) физического объема (количества) проданных фруктов;
3) цен, используя взаимосвязь индексов.
Сформулируйте выводы.
Вариант второй (выполняют студенты, фамилии которых начинаются с букв Б, Р, Ч)
Задача 1. В целях изучения стажа рабочих завода проведена 36%-ная механическая выборка, в результате которой получено следующее распределение рабочих по стажу работы:
| Стаж, число лет | Число рабочих, чел. |
| до 5 | 12 |
| 5-10 | 18 |
| 10-15 | 24 |
| 15-20 | 32 |
| 20-25 | 6 |
| 25 и выше | 8 |
| Итого: | 100 |
На основе этих данных вычислите:
1) средний стаж рабочих завода;
2) моду и медиану стажа рабочих;
3) средний квадрат отклонений (дисперсию), среднее квадратическое отклонение и коэффициент вариации;
4) с вероятностью 0,997 предельную ошибку выборочной средней и возможные границы, в которых ожидается средний стаж рабочих всего завода;
5) с вероятностью 0,954 предельную ошибку выборочной доли и границы удельного веса рабочих со стажем работы от 10 лет и выше в общей численности рабочих.
Задача 2. Имеются следующие данные о производстве станков на станкостроительном заводе:
| Год | Производство станков, шт. |
| 2004 | 1250 |
| 2005 | 1263 |
| 2006 | 1252 |
| 2007 | 1270 |
| 2008 | 1284 |
Для анализа динамики производства станков вычислите:
1) абсолютные приросты, темпы роста и прироста по годам и к 2004 г., абсолютное содержание одного процента прироста (снижения) по годам. Полученные показатели представьте в таблице;
2) среднегодовое производство станков за 2004–2008 гг.,
3) среднегодовые: абсолютный прирост, темп роста и темп прироста производства станков за анализируемый период.
Постройте график динамики производства станков за 2004–2008 гг. Сформулируйте выводы.
Задача 3. Динамика средних цен и объема продажи на двух рынках города характеризуется следующими данными:
| Продукция | Продано продукции, тыс. кг. | Средняя цена за кг, руб. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| Рынок №1 | ||||
| Картофель | 4,0 | 4,2 | 640 | 760 |
| Капуста | 2,5 | 2,4 | 720 | 840 |
| Рынок №2 | ||||
| Картофель | 10,0 | 12,0 | 760 | 700 |
На основании имеющихся данных вычислите:
1. Для рынка №1 (по двум видам продукции вместе):
а) общий индекс товарооборота;
б) общий индекс цен;
в) общий индекс физического объема товарооборота;
Определите в отчетном периоде по сравнению с базисным абсолютный прирост товарооборота и разложите его по факторам (за счет изменения цен и объема продаж товаров).
Покажите взаимосвязь между исчисленными индексами.
2. Для двух рынков вместе (по картофелю):
а) индекс цен переменного состава;
б) индекс цен постоянного состава;
в) индекс влияния изменения структуры объема продаж картофеля на динамику средней цены.
Объясните различие между полученными величинами индексов постоянного и переменного состава.
Определите общее абсолютное изменение средней цены картофеля в отчетном периоде по сравнению с базисным и разложите его по факторам: за счет непосредственного изменения уровней цен и изменения структуры продажи картофеля.
Сформулируйте выводы.
Задача 4. Имеются данные о производстве продукции на сахарном заводе:
| Продукция | Стоимость продукции в базисном периоде, млн. р. | Изменение количества произведенной продукции в отчетном периоде по сравнению с базисным, % |
| Сахар-песок | 37380 | +10 |
| Меласса | 3100 | -3 |
| Жом свежий | 580 | +5 |
Вычислите:
1) общий индекс физического объема продукции;
2) используя взаимосвязь индексов, определите, на сколько процентов изменились цены на произведенную продукцию, если известно, что стоимость продукции в фактических ценах возросла на 30%.
Вариант третий (выполняют студенты, фамилии которых начинаются с букв В, П, Ц)
Задача 1. В целях изучения норм расходования сырья при изготовлении продукции на заводе проведена 19%-ная механическая выборка, в результате которой получено следующее распределение изделий по массе:
| Масса изделия, г | Число изделий, шт. |
| до 40 | 8 |
| 40–42 | 18 |
| 42–44 | 45 |
| 44–46 | 17 |
| 46 и выше | 12 |
| Итого: | 100 |
На основе этих данных вычислите:
1) среднюю массу изделия;
2) моду и медиану массы изделия;
3) средний квадрат отклонений (дисперсию), среднее квадратическое отклонение и коэффициент вариации;
4) с вероятностью 0,997 предельную ошибку выборочной средней и возможные границы, в которых ожидается средняя масса изделия во всей партии изготовленных изделий;
5) с вероятностью 0,954 предельную ошибку выборочной доли и границы удельного веса стандартных изделий с массой изделия от 40 до 46 граммов в общем объеме готовой продукции.
Задача 2. Реализация фотоаппаратов в магазинах города характеризуется следующими данными:
| Год | Продано фотоаппаратов, тыс. шт. |
| 2004 | 250 |
| 2005 | 265 |
| 2006 | 255 |
| 2007 | 268 |
| 2008 | 272 |
Для анализа динамики реализации фотоаппаратов вычислите:
1) абсолютные приросты, темпы роста и темпы прироста по годам и к 2004 г., абсолютное содержание одного процента прироста (снижения) по годам. Полученные показатели представьте в таблице;
2) среднегодовую реализацию фотоаппаратов за 2004–2008 гг.;
3) среднегодовые: абсолютный прирост, темп роста и темп прироста реализации фотоаппаратов за анализируемый период.
Постройте график динамики реализации фотоаппаратов за 1998–2002 годы. Сформулируйте выводы.
Задача 3. Динамика себестоимости и объема производства продукции характеризуется следующими данными:
| Продукция | Выработано продукции, тыс. ед. | Себестоимость единицы продукции, тыс. руб. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| Завод №1 | ||||
| КД-5 | 25 | 25 | 50 | 58 |
| КО-3 | 10 | 12 | 90 | 88 |
| Завод №2 | ||||
| КД-5 | 40 | 45 | 70 | 75 |
На основании имеющихся данных вычислите:
1. Для завода №1 (по двум видам продукции вместе):
а) общий индекс затрат на производство продукции;
б) общий индекс себестоимости продукции;
в) общий индекс физического объема производства продукции.
Определите в отчетном периоде по сравнению с базисным абсолютное изменение суммы затрат на производство продукции и разложите его по факторам (за счет изменения себестоимости и объема выработанной продукции).
Покажите взаимосвязь между исчисленными индексами.
2. Для двух заводов вместе (по продукции КД-5):
а) индекс себестоимости переменного состава;
б) индекс себестоимости постоянного состава;
в) индекс влияния изменения структуры производства продукции на динамику средней себестоимости.
Объясните различие между полученными величинами индексов постоянного и переменного состава.
Определите общее абсолютное изменение средней себестоимости единицы продукции в отчетном периоде по сравнению с базисным и разложите его по факторам: за счет непосредственного изменения уровней себестоимости и изменения структуры производства продукции. Сформулируйте выводы.
Задача 4. Имеются следующие данные о продаже картофеля и фруктов:
| Товарная группа |
Продано в фактических ценах, млн. р. |
|
| базисный период | отчетный период | |
| Картофель | 65 | 72,8 |
| Фрукты | 35 | 43,2 |
В отчетном периоде по сравнению с базисным цены на картофель повысились на 12%, а на фрукты – на 8%.
Вычислите:
1) общий индекс товарооборота в фактических ценах;
2) общий индекс цен и сумму дополнительных расходов населения в отчетном периоде при покупке картофеля и фруктов;
3) общий индекс физического объема товарооборота, используя взаимосвязь индексов.
Вариант четвертый (выполняют студенты, фамилии которых начинаются с букв Г, О, Ф )
Задача 1. В целях изучения дневной выработки рабочими завода проведена 20%-ная случайная бесповторная выборка, в результате которой получено следующее распределение рабочих:
| Группы рабочих с дневной выработкой изделий, шт. | Число рабочих, чел. |
| до 30 | 4 |
| 30–34 | 15 |
| 34–38 | 30 |
| 38–42 | 26 |
| 42–46 | 15 |
| 46 и выше | 10 |
| Итого: | 100 |
На основе этих данных вычислите:
1) среднедневную выработку изделий;
2) моду и медиану дневной выработки;
3) средний квадрат отклонений (дисперсию), среднее квадратическое отклонение и коэффициент вариации;
4) с вероятностью 0,954 предельную ошибку выборочной средней и возможные границы, в которых ожидается среднедневная выработка изделий всеми рабочими завода;
5) с вероятностью 0,683 предельную ошибку выборочной доли и границы удельного веса рабочих с дневной выработкой свыше 42 изделий среди всех рабочих завода.
Задача 2. Производство радиоприемников на заводе характеризуется следующими данными:
| Год | Произведено радиоприемников, тыс. шт. |
| 2004 | 50 |
| 2005 | 54 |
| 2006 | 55 |
| 2007 | 52 |
| 2007 | 56 |
Для анализа динамики производства радиоприемников вычислите:
1) абсолютные приросты, темпы роста и темпы прироста по годам и к 1998 г., абсолютное содержание одного процента прироста (снижения) по годам. Полученные показатели представьте в виде таблицы;
2) среднегодовое производство радиоприемников за 2004–2008 гг.
3) среднегодовые: абсолютный прирост, темп роста и темп прироста производства радиоприемников за анализируемый период.
Постройте график динамики производства радиоприемников за 1998–2002 г. Сформулируйте выводы.
Задача 3. Динамика средних цен и объема продажи на двух рынках города характеризуется следующими данными:
| Наименование продукта | Продано продуктов, ед. | Средняя цена за единицу, тыс. р. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| Рынок №1 | ||||
| Молоко, л. | 500 | 1000 | 0,85 | 1,10 |
| Творог, кг. | 200 | 220 | 3,0 | 3,8 |
| Рынок №2 | ||||
| Молоко, л. | 600 | 700 | 0,8 | 0,96 |
На основании имеющихся данных вычислите:
1. Для рынка №1 (по двум видам продукции вместе):
а) общий индекс выручки от реализации продуктов;
б) общий индекс цен;
в) общий индекс физического объема проданных продуктов.
Определите в отчетном периоде по сравнению с базисным абсолютный прирост выручки от реализации продуктов и разложите его по факторам (за счет изменения цен и объема продажи продуктов).
Покажите взаимосвязь между исчисленными индексами.
2. Для двух рынков вместе (по молоку);
а) индекс цен переменного состава;
б) индекс цен постоянного состава;
в) индекс влияния изменения структуры объема продаж молока на динамику средней цены.
Объясните различие между полученными величинами индексов постоянного и переменного состава.
Определите общее абсолютное изменение средней цены молока в отчетном периоде по сравнению с базисным и разложите его по факторам: за счет непосредственного изменения уровней цен и изменения структуры продажи молока. Сформулируйте выводы.
Задача 4. Имеются следующие данные о затратах на производство продукции и об изменении ее количества на обувной фабрике:
| Продукция | Общие затраты на производство обуви, млн. р. | Изменение количества произведенной обуви в III кв. по сравнению со II кв., % | |
| II квартал | III квартал | ||
| Обувь мужская | 2605 | 2708 | -5 |
| Обувь женская | 3088 | 3124 | +2 |
| Обувь детская | 1594 | 1606 | Без изменений |
Вычислите:
1) общий индекс затрат на производство обуви;
2) общий индекс физического объема производства обуви;
3) общий индекс себестоимости производства обуви, используя взаимосвязь индексов.
Вариант пятый (выполняют студенты, фамилии которых начинаются с букв Д, Н, У)
Задача 1. В целях изучения затрат времени на изготовление одной детали рабочими завода проведена 19%- ная случайная бесповторная выборка, в результате которой получено следующее распределение деталей по затратам времени:
| Затраты времени на одну деталь, мин. | Число деталей, шт. |
| до 20 | 7 |
| 20–22 | 14 |
| 22–24 | 48 |
| 24–26 | 18 |
| 26 и более | 13 |
| Итого: | 100 |
На основе этих данных вычислите:
1) средние затраты времени на изготовление одной детали;
2) моду и медиану затрат времени;
3) средний квадрат отклонений (дисперсию), среднее квадратическое отклонение и коэффициент вариации;
4) с вероятностью 0,997 предельную ошибку выборочной средней и возможные границы, в которых ожидаются средние затраты времени на изготовление одной детали на заводе;
5) с вероятностью 0,954 предельную ошибку выборочной доли и границы удельного веса числа деталей с затратами времени на их изготовление от 20 до 26 мин в общем количестве деталей, изготовленных на заводе.
Задача 2. Производство настенных часов на часовом заводе характеризуется следующими данными:
| Год | Производство часов, тыс. шт. |
| 2004 | 180 |
| 2005 | 186 |
| 2006 | 180 |
| 2007 | 188 |
| 2008 | 192 |
Для анализа динамики производства часов вычислите:
1) абсолютные приросты, темпы роста и темпы прироста по годам и к 2004 г., абсолютное содержание одного процента прироста (снижения) по годам. Полученные показатели представьте в таблице;
2) среднегодовое производство настенных часов за 2004–2008 гг.
3) среднегодовые: абсолютный прирост, темп роста и темп прироста производства настенных часов за анализируемый период.
Постройте график динамики производства настенных часов за 1998–2002гг. Сформулируйте выводы.
Задача 3. Динамика себестоимости и объема производства продукции заводов характеризуется следующими данными:
| Продукция | Выработано продукции, тыс. ед. | Себестоимость единицы продукции, млн. р. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| Завод №1 | ||||
| ОМ-95 | 16 | 16 | 3.0 | 3.3 |
| КС-73 | 6 | 7 | 4.3 | 4.5 |
| Завод №2 | ||||
| ОМ-95 | 20 | 24 | 4.0 | 4.2 |
На основании имеющихся данных вычислите:
1. Для завода №1 (по двум видам продукции вместе):
а) общий индекс затрат на производство продукции;
б) общий индекс себестоимости продукции;
в) общий индекс физического объема производства продукции.
Определите в отчетном периоде по сравнению с базисным абсолютное изменение суммы затрат на производство продукции и разложите его по факторам (за счет изменения себестоимости и объема выработанной продукции).
Покажите взаимосвязь между исчисленными индексами.
2. Для двух заводов вместе (по продукции ОМ-95):
а) индекс себестоимости переменного состава;
б) индекс себестоимости постоянного состава;
в) индекс влияния изменения структуры производства продукции на динамику средней себестоимости.
Объясните различие между полученными величинами индексов постоянного и переменного состава.
Определите общее абсолютное изменение средней себестоимости единицы продукции в отчетном периоде по сравнению с базисным и разложите его по факторам: за счет непосредственного изменения себестоимости единицы продукции и изменения структуры производства. Сформулируйте выводы.
Задача 4. Имеются следующие данные о товарообороте магазина потребительской кооперации:
| Товарная группа | Продано товаров в фактических ценах, млн. р. | Индекс цен во II квартале по сравнению с I кварталом | |
| I квартал | II квартал | ||
| Хлеб и хлебобулочные | |||
| изделия | 820 | 896 | 1.2 |
| Кондитерские изделия | 980 | 1199 | 1.09 |
| Цельномолочная | |||
| продукция | 700 | 900 | 1.2 |
Вычислите:
1) общий индекс товарооборота в фактических ценах;
2) общий индекс цен;
3) общий индекс физического объема продажи товаров, используя взаимосвязь индексов.
Как повлияло изменение цен на величину товарооборота во втором квартале по сравнению с первым кварталом в абсолютном и относительным выражении.
Вариант шестой (выполняют студенты, фамилии которых начинаются с букв Е, М, С, Ш)
Задача 1. В целях изучения урожайности озимой пшеницы в колхозах области проведено 19%-ное выборочное обследование 100 га посевов, отобранных в случайном порядке, в результате которого получены следующие данные (выборка бесповторная):
| Урожайность, ц с одного га. | Посевная площадь, га. |
| до 20 | 5 |
| 20–24 | 20 |
| 24–28 | 35 |
| 28–32 | 30 |
| 32 и выше | 10 |
| Итого: | 100 |
На основе этих данных вычислите:
1) среднюю урожайность озимой пшеницы с 1 га;
2) моду и медиану урожайности озимой пшеницы
3) средний квадрат отклонений (дисперсию), среднее квадратическое отклонение и коэффициент вариации;
4) с вероятностью 0,954 предельную ошибку выборочной средней и возможные границы, в которых ожидается средняя урожайность озимой пшеницы во всей области;
5) с вероятностью 0,997 предельную ошибку выборочной доли и границы удельного веса посевных площадей во всей области с урожайностью от 28 ц с 1га и выше.
Задача 2. Реализация электропылесосов в магазинах района характеризуется следующими данными:
| Год | Продано электропылесосов, тыс. шт. |
| 2004 | 42 |
| 2005 | 44 |
| 2006 | 40 |
| 2007 | 43 |
| 2008 | 47 |
Для анализа динамики реализации электропылесосов вычислите:
1) абсолютные приросты, темпы роста и темпы прироста по годам и к 2004 г., абсолютное содержание одного процента прироста (снижения) по годам. Полученные показатели представьте в таблице;
2) среднегодовую реализацию электропылесосов за 2004–2008гг.;
3) среднегодовые абсолютный прирост, темп роста и темп прироста реализации электропылесосов, за анализируемый период.
Постройте график динамики реализации электропылесосов за 2004-2008 гг. Сформулируйте выводы:
Задача 3. Динамика средних цен и объема продажи на двух рынках города характеризуется следующими данными:
| Овощи | Продано овощей, кг. | Средняя цена за кг, тыс. р. | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| Рынок №1 | ||||
| Огурцы | 2500 | 2800 | 0,8 | 0,95 |
| Помидоры | 1700 | 2100 | 3,02 | 2,8 |
| Рынок №2 | ||||
| Огурцы | 4200 | 4000 | 1,28 | 1,45 |
На основании имеющихся данных вычислите:
1. Для рынка №1 (по двум видам овощей вместе):
а) общий индекс выручки от реализации овощей;
б) общий индекс цен;
в) общий индекс физического объема проданных овощей.
Определите в отчетном периоде по сравнению с базисным абсолютный прирост выручки от реализации овощей и разложите его по факторам (за счет изменения цен и объема продажи овощей).
Покажите взаимосвязь между исчисленными индексами.
2. Для двух рынков вместе (по огурцам):
а) индекс цен переменного состава;
б) индекс цен постоянного состава;
в) индекс влияния изменения структуры объема продаж огурцов на динамику средней цены.
Объясните различие между полученными величинами индексов постоянного и переменного состава.
Определите общее абсолютное изменение средней цены огурцов в отчетном периоде по сравнению с базисным и разложите его по факторам: за счет непосредственного изменения уровней цен огурцов и за счет изменения структуры продажи огурцов. Сформулируйте выводы.
Задача 4. Имеются следующие данные о затратах на производство трех видов продукции и об изменении ее себестоимости:
| Изделия |
Общие затраты на производство продукции, млн. р. |
Изменение себестоимости единицы продукции в III квартале по сравнению с II кварталом, % | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| II квартал | III квартал | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
АВычислите: 1) общий индекс затрат на производство продукции; 2) общий индекс себестоимости продукции; 3) общий индекс физического объема производства продукции, используя взаимосвязь индексов. Как повлияло изменение себестоимости на величину затрат на производство продукции в III кв. по сравнению со II кв. в абсолютном выражении и относительном выражении Вариант седьмой (выполняют студенты, фамилии которых начинаются с букв Ж, Л, Т, Ю) Задача 1. В целях изучения степени выполнения норм выработки на машиностроительном заводе было проведено 10%-ное выборочное обследование рабочих-сдельщиков, в результате которого получены следующие данные (отбор механический):
На основе этих данных вычислите: 1) средний процент выполнения норм выработки одним рабочим- сдельщиком; 2) моду и медиану выполнения норм выработки; 3) средний квадрат отклонений (дисперсию), среднее квадратическое отклонение и коэффициент вариации; 4) с вероятностью 0,954 предельную ошибку выборочной средней и возможные границы, в которых ожидается средний процент выполнения норм выработки среди всех рабочих-сдельщиков завода; 5) с вероятностью 0,997 предельную ошибку выборочной доли и границы удельного веса рабочих – сдельщиков всего завода, выполняющих нормы выработки на 130% и выше. Задача 2. Издание учебной литературы для вузов в издательстве характеризуется следующими данными:
Для анализа динамики издания учебной литературы для вузов вычислите: 1) абсолютные приросты, темпы роста и темпы прироста по годам и к 2004 г., абсолютное содержание одного процента прироста (снижения) по годам. Полученные показатели представьте в таблице; 2) среднегодовое издание учебной литературы для вузов за 2004–2008гг. 3) среднегодовые: абсолютный прирост, темп роста и темп прироста издания учебной литературы для вузов за анализируемый период; Постройте график динамики издания учебной литературы для вузов за 2004–2008 годы. Сформулируйте выводы. Задача 3. Продажа яблок и груш на двух рынках города характеризуется следующими данными:
|