Дипломная работа: Разработка инвестиционного проекта ОАО "Завод по производству труб большого диаметра"

Аннотация

В данной дипломной работе представлена модель, предназначенная для оценки риска инвестиционного проекта.

Модель разрабатывалась с применением теории нечетких множеств. Для оценки риска инвестиционного проекта предложено использовать три критерия, имеющие четкие значения. Модель выдает выходную переменную «уровень риска проекта» также в четком виде. Внутренняя же структура модели является нечеткой.

Представленная модель реализована программно, а предложенный метод принятия решения может быть успешно использован при оценке риска.

Для анализа эффективности работы модели были также программно реализованы модель оценки риска проекта на основе вероятностного подхода и имитационная модель возможных сценариев значений денежных потоков.

Сравнение работы моделей приведено с помощью таблиц, на основе которых сравнивается оцененный риск проекта, а также значения ежегодного чистого приведенного эффекта.

Дипломная работа изложена на 113 страницах, содержит 3 рисунка, 15 таблиц. Список использованных источников состоит из 25 наименований, 3 приложений.

Содержание

Введение 7

1 Аналитический обзор литературы 8

1.1 Основные понятия инвестиционного проектирования 8

1.1.1 Понятие проекта и проектного цикла 8

1.1.2 Оценка текущей стоимости денег 9

1.1.3 Общая характеристика методов оценки эффективности инвестиционного проекта 11

1.2 Общие понятия неопределенности и риска 12

1.3 Виды рисков 13

1.4 Мера риска 18

1.5 Методы анализа рисков 18

1.5.1 Метод корректировки нормы дисконта 18

1.5.2 Анализ чувствительности 19

1.5.3 Анализ сценариев 20

1.5.4 Анализ вероятностных распределений потоков платежей 20

1.5.5 Деревья решений 20

1.5.6 Имитационное моделирование (метод Монте-Карло) 21

1.5.7 Модель оценки риска стратегического инвестиционного проекта 22

1.5.8 Метод нечетко-множественной оценки инвестиционного проекта 25

2 Специальная часть 29

2.1 Описание модели оценки риска инвестиционного проекта для ОАО «Завод по производству труб большого диаметра» на основе модели риска стратегического инвестиционного проекта 29

2.2 Проблемы, возникающие при использовании метода оценки риска инвестиционного проекта, основанном на вероятностном подходе. 31

2.3 Имитационная модель получения возможных сценариев величин денежных потоков 32

2.4 Построение модели оценки риска инвестиционного проекта при нечетких входных данных 33

2.5 Описание нечетко-моножественной модели принятия решения для сложных систем 35

2.6 Описание нечетких данных для модели принятия решения о риске инвестиционного проекта 38

3 Анализ результатов 46

3.1 Обоснование выбора среды программирования 46

3.2. Описание программы 46

3.3 Оценка риска инвестиционного проекта ОАО «Завод по производству труб большого диаметра» с применением теории вероятностей 49

3.4 Применение математического аппарата нечетких множеств для оценки риска проекта 52

4 Безопасность жизнедеятельности 59

4.1 Идентификация опасных и вредных производственных факторов 59

4.2 Санитарно-технические требования 61

4.2.1 Требования к планировке помещения 61

4.2.2 Требования к микроклимату помещения 62

4.2.3 Требования к освещению помещения 62

4.2.4 Требования безопасности при эксплуатации электрокоммуникаций 64

4.3 Разработка мер защиты от опасных и вредных факторов 64

4.4 Безопасность жизнедеятельности в чрезвычайных ситуациях 65

4.5 Инженерная разработка. Расчет защитного зануления персонального компьютера 66

5 Охрана природной окружающей среды 69

5.1 Стандарты безопасности 69

5.2 Эргономические требования 71

5.3 Стандарты уровней излучения 72

5.3.1 Требования к электромагнитным излучениям и энергопотреблению 72

5.3.2 Рентгеновское излучение 72

5.3.3 Электростатический потенциал 72

5.3.4 Переменное электрическое поле 72

5.3.5 Переменное магнитное поле 72

5.3.6 Энергосбережение 73

5.4 Требования к электрической безопасности 73

5.5 Дополнительные требования 73

5.5.1 Наклон в вертикальной плоскости 73

5.5.2 Регулировка высоты 73

5.5.3 Поворот в горизонтальной плоскости 73

5.5.4 Регулировка яркости и контраста 74

5.5.5 Индикация частоты вертикальной развертки 74

5.5.6 Акустический шум (для ВДТ с вентилятором) 74

5.6 Экологические стандарты 74

5.7 Стандарты пониженного энергопотребления 75

5.8 Экологическая оценка компьютера как объекта загрязнения окружающей среды. 76

Выводы 78

Список использованных источников 79

Приложение А. Основные элементы пользовательского интерфейса 81

Приложение Б. Текст программы 86

Приложение В. Данные о значениях ковариаций и дисперсий чистых денежных потоков, полученные в результате работы программы 113

Введение

Инвестиционный проект предполагает планирование во времени трех основных денежных потоков: потока инвестиций, потока текущих (операционных) платежей и потока поступлений. Поток текущих платежей и поток поступлений не могут быть спланированы вполне точно, поскольку нет и не может быть полной определенности относительно будущего состояния рынка. Цена и объемы реализуемой продукции, цены на сырье и материалы и прочие денежно-стоимостные параметры среды по факту их осуществления в будущем могут также сильно отличаться от предполагаемых плановых значений, которые оцениваются с позиций сегодняшнего дня.

Неустранимая информационная неопределенность влечет столь же неустранимый риск принятия инвестиционных решений. Всегда остается возможность того, что проект, признанный состоятельным, позже окажется убыточным, поскольку достигнутые в ходе инвестиционного процесса значения параметров отклонились от плановых, или же какие-либо факторы вообще не были учтены. Инвестор не располагает всеобъемлющей оценкой риска, так как число разнообразий внешней среды всегда превышает управленческие возможности лица принимающего решения, что предполагает наличие слабоожидаемого сценария развития событий, который, будучи неучтен в проекте, тем не менее, может состояться и сорвать инвестиционный процесс. В то же время инвестору необходимо измерять рискованность своих инвестиционных решений как на стадии разработки проекта, так и в ходе инвестиционного процесса, чтобы повышать уровень своей осведомленности. Если степень риска будет расти до недопустимых значений, а инвестор не будет об этом знать, то он обречен действовать вслепую.

. В общем случае анализ рисков представляет собой достаточно трудоемкую процедуру, требующую рассмотрения большого количества альтернативных вариантов реализации проекта и построения для каждого варианта детальной модели финансовых потоков. В связи с этим несомненный практический интерес (с точки зрения экономии времени и ресурсов) представляют методы экспресс-анализа уровня риска инвестиционных проектов и оценка его устойчивости во времени. Разработка модели решения этой проблемы является целью настоящей работы.

1 Аналитический обзор литературы

1.1 Основные понятия инвестиционного проектирования

1.1.1 Понятие проекта и проектного цикла

В международной практике план развития предприятия представляется в виде специальным образом оформленного бизнес-плана, который, по существу, представляет собой структурированное описание проекта развития предприятия. Если проект связан с привлечением инвестиций, то он носит название “инвестиционного проекта”. Обычно любой новый проект предприятия в той или иной мере связан с привлечением новых инвестиций. В наиболее общем понимании проект - это специальным образом оформленное предложение об изменении деятельности предприятия, преследующее определенную цель.

В /1/ автор подразделяет проекты на тактические и стратегические. К числу последних он относит проекты, предусматривающие изменение формы собственности (создание арендного предприятия, акционерного общества, частного предприятия, совместного предприятия и т.д.), или кардинальное изменение характера производства (выпуск новой продукции, переход к полностью автоматизированному производству и тому подобное). Тактические проекты автор связывает с изменением объемов выпускаемой продукции, повышением качества продукции, модернизацией оборудования.

Поскольку дипломная работа связана с оценкой рисков стратегических инвестиционных проектов, то рассмотрим последние более подробно.

В /2/ дано определение стратегического инвестиционного проекта как спланированной на длительный срок системы мер и мероприятий, направленных на привлечение материальных и финансовых ресурсов, и их поэтапное вложение с целью получения заданного эффекта. Автор выделяет основные качественные критерии стратегических инвестиционные проектов:

- большой объем связываемых финансовых средств в сопоставлении с собственными средствами субъекта инвестиций;

- высокая степень неопределенности (риска) промежуточных и окончательных результатов внедрения проекта;

- низкая ликвидность инвестиционного проекта (невозможности продажи-переуступки с ограниченными финансовыми потерями третьей стороне)

- высокая экономическая значимость инвестиционного проекта.

Промежуток времени между моментом появления проекта и моментом его ликвидации называется проектным или жизненным циклом проекта. Весь проектный цикл разбивается на несколько этапов. Жизненные циклы инвестиционных проектов разделяются авторами в /1,2,3/ на этапы, которые, в общем, можно охарактеризовать так:

- Обоснование – на этом этапе происходит разработка идеи проекта, его содержательной части;

- Оценка – проводится полномасштабная оценка будущей эффективности проекта по критерию абсолютной и относительной выгодности как с использованием стандартных статистических и динамических моделей в условиях риска, так и с применением оригинальных моделей, созданных с учетом специфики проекта;

- Выбор – на этом этапе производится отбор одного или нескольких проектов по результатам этапа оценки в соответствии с критериями оптимальности (эффективности);

- Реализация – осуществляется управление мерами и мероприятиями в рамках проекта, оценка риск-факторов проекта, их минимизация и контроль в динамике;

- Оценка результатов – данный этап подразумевает экономическую оценку и обобщение результатов после завершения проекта.

Началом реализации проекта является принятие решения о начале инвестирования, а концом - либо достижение всех поставленных целей, либо вынужденное прекращение осуществления проекта. Реализация проекта – это растянутое во времени и непрерывное действие. Но в целях моделирования всю реализацию разбивают на несколько временных этапов, интервалов планирования. Для каждого интервала составляется свой бюджет, то есть смета всех поступлений и платежей, связанных с данным инвестированием. Рассчитанная для отдельных моментов времени разница поступлений и выплат называется чистым платежом. Поступления – это выручка от реализации произведенной за счет инвестирования продукции, а платежи – это расходы на производство этой продукции (производственные затраты) и инвестиционные затраты. На начальном этапе проекта сальдо обычно отрицательное, так как инвестиционные затраты значительно больше поступлений, а на завершающих этапах, когда инвестиции уже приносят значительный доход, - положительное.

1.1.2 Оценка текущей стоимости денег

В /1/ автор отмечает, что международная практика оценки эффективности инвестиций базируется на концепции временной стоимости денег. Инвестируемый капитал, равно как и денежный поток, приводится к настоящему времени или к определенному расчетному году (который, как правило, предшествует началу реализации проекта). Отсюда возникает еще одно важнейшее понятие, непосредственно связанное с инвестиционным проектированием - это дисконтирование (discounting). В /4/ автор определяет дисконтирование как приведение разновременных экономических показателей к какому-либо одному времени – точке приведения. С помощью этой операции производится приведение всех денежных потоков к общей единице измерения. Общая единица измерения необходима потому, что капитал в различные интервалы времени имеет различную стоимость. Предполагается, что каждый период капитал Vt₀ способен приносить доход в размере Vt_0*r, где r – процентная ставка (ставка дисконтирования). Вполне понятно, что будущая стоимость (future value) капитала должна включать в себя доход, который принесет капитал, то есть

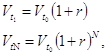(1)

где V_t₁ – величина капитала через один год, денежные единицы;

V_tN – величина капитала через N периодов, денежные единицы.

Исходя из этих равенств, производится расчет текущей стоимости PV (present value). Теоретически можно привести все величины к любому временному этапу t

(2)

но, в последующем, удобнее работать именно с начальным, или нулевым, периодом

(3)

Приводя денежные потоки к одному интервалу времени, а, следовательно, и к одной единице измерения, получаем возможность производить над ними математические вычисления. Важно понять, что денежные потоки в разные периоды времени имеют разные единицы измерения, и использование ставки дисконтирования позволяет перейти к одной единице измерения. Именно эта операция дает нам возможность складывать денежные потоки разных периодов.

За ставку дисконтирования можно принимать различные процентные ставки. Эти ставки отражают разные способы оценки разницы стоимости капитала в определенные интервалы времени. За ставку дисконтирования могут приниматься:

- минимальная доходность альтернативного безрискового способа использования капитала (например, ставка процента по надежным ценным бумагам или ставка процента по депозиту в надежном банке);

- существующий уровень доходности капитала в компании;

- стоимость капитала, который может быть использован для данного инвестиционного проекта (например, ставка по инвестиционному кредиту).

Выбранная ставка дисконтирования во многом влияет на оценку эффективности проекта.

1.1.3 Общая характеристика методов оценки эффективности инвестиционного проекта

В /1/ автор отмечает, что суть всех методов оценки эффективности инвестиционного проекта базируется на следующей простой схеме: исходные инвестиции при реализации какого-либо проекта генерируют денежный поток CF₁, CF₂, ... , CF_n. Инвестиции признаются эффективными, если этот поток достаточен для возврата исходной суммы капитальных вложений и обеспечения требуемой отдачи на вложенный капитал.

Наиболее распространены следующие показатели эффективности капитальных вложений:

- дисконтированный срок окупаемости (DPB).

- чистый современный эффект (чистая приведенная стоимость) инвестиционного проекта (NPV),

- внутренняя норма прибыльности (доходности, рентабельности) (IRR),

определения которых можно найти, например, в /1,2,5/. Поскольку в данной дипломной работе используется значение чистого современного эффекта, то приведем его определение.

Чистый современный эффект – сумма всех дисконтируемых и ревальвируемых на какой-либо момент времени поступлений и выплат, возникших в результате реализации инвестиционного проекта /2/. Тогда соотношение для NPV имеет следующий вид

(4)

где I - стартовый объем инвестиций, денежные единицы;

N - число плановых интервалов (периодов) инвестиционного процесса, соответствующих сроку жизни проекта;

DV_i - оборотное сальдо поступлений и платежей в i-ом периоде, денежные единицы;

r_i - ставка дисконтирования, выбранная для i-го периода с учетом оценок ожидаемой стоимости используемого в проекте капитала (например, ожидаемая ставка по долгосрочным кредитам).

Инвестиционный проект признается эффективным, когда NPV, оцененная по (4), больше определенного проектного уровня G.

В /6/ автор отмечает, что в самом распространенном случае G = 0, так как проект обычно считается эффективным, если дисконтированная стоимость поступлений не меньше дисконтированной стоимости расходов. Однако в реальной жизни все не совсем так. Предприятие, реализуя какой-либо проект, может руководствоваться не только соображениями относительно среднесрочной коммерческой эффективности, но и учитывать долгосрочные возможности или преследовать социальные и другие интересы, например, увеличение числа рабочих мест, улучшение условий труда работников. Таким образом, предприятие может позволить величине G быть равной величине меньше нуля. Или же, наоборот, учитывая неблагоприятные последствия проекта социального или экологического характера, предприятие устанавливает величину G на уровне G>0. То есть, фактически, предприятие устанавливает величину G в зависимости от внешних эффектов, связанных с проектом.

Данные показатели, равно как и соответствующие им методы, используются в двух вариантах:

- для определения эффективности независимых инвестиционных проектов (так называемая абсолютная эффективность), когда делается вывод о том принять проект или отклонить,

- для определения эффективности взаимоисключающих друг друга проектов (сравнительная эффективность), когда делается вывод о том, какой проект принять из нескольких альтернативных.

1.2 Общие понятия неопределенности и риска

В /4/ автор определяет неопределенность как неполноту или неточность информации об условиях, связанных с исполнением отдельных плановых решений, за которыми могут быть определенные потери.

Автор указывает, что чаще всего в практике можно наблюдать три разновидности неопределенностей:

- незнание всего того, что может повлиять на деятельность организации. Изучить все не только сложно, но экономически невыгодно;

- случайность – в любом прогнозируемом событии могут быть отклонения в результате каких-то случайных внешних воздействий. Это и отказ работы какого-то технического аппарата, срыв в материально-техническом обеспечении процесса производства, и провал в инвестировании в отдельной сфере, и многое другое;

- неопределенность противодействия – для организации это непредсказуемое поведение конкурентов и заказчиков продукции. Могут также быть: срыв в исполнении договорных обязательств по поставкам, неисполнение финансовых обязательств банками, забастовки и некоторые другие разногласия и конфликты в трудовых коллективах.

Неопределенность порождает неблагоприятные ситуации и последствия, которые характеризуются понятием «риск». В /1,2,4,7/ авторы дают различные определения понятия риска, которые, в основном, сводятся к следующему: риск - это вероятность (угроза) потери лицом или организацией части своих ресурсов, недополучения доходов или появления дополнительных расходов в результате осуществления определенной производственной и финансовой политики.

Под управлением хозяйственным риском автор в /2/ понимает процесс выявления уровня неопределенности, отклонений в прогнозируемом результате, принятия нестандартного решения и осуществления системы ведения хозяйства, позволяющего предотвращать, уменьшать отрицательное воздействие стохастических факторов на результаты хозяйственной деятельности и получать доход.

Качественная оценка риска – определение видов риска, факторов, влияющих на его уровень при осуществлении определенной хозяйственной деятельности, а также установление методологии количественной оценки.

Количественная оценка риска проекта осуществляется путем нахождения его уровня риска с помощью методов теории вероятностей, математической статистики и построения системы математических моделей для конкретного проекта.

Комбинированная оценка риска проекта включает в себя качественную и количественную оценку.

1.3 Виды рисков

В различных источниках /1,2,4,5,7,8/ даются различные классификации видов риска, которые все объединяют одни и те же виды, но с некоторыми особенностями их распределения по группам. Приведем наиболее полную системную классификацию видов хозяйственных рисков, представленную в /2/. Она сведена в таблице 1.

Таблица 1 – Системная классификация хозяйственных рисков

Классификационные признаки	Виды рисков	Характеристика риска
1	2	3
Природа возникновения	Субъективные (связанные с субъектом хозяйствования)	Неразвитые способности к риску; недостаток опыта, образования, профессионализма, необоснованные амбиции и так далее. Или наоборот высокий уровень способностей, образования, профессионализма и тому прочее
	Объективные	Недостаток информации, стихийные бедствия, неожиданные изменения конъюнктуры рынка, уровня инфляции, в законодательстве, кредитовании, налогообложении и так далее
Этапы решения проблемы	На этапе принятия решений	Незнание применения методов определения уровня риска из-за недостатка информации, ее низкого качества, использования дезинформации. Или, наоборот, отличное владение методами решения, использования качественной информации
	На этапе реализации решения	Ошибки в реализации правильного решения, неожиданные изменения субъективных условий
По уровню	Локальный	Риск на уровне отдельной фирмы, компании, объединения, их структурных звеньев
Отраслевой	Риск, связанный со спецификой отрасли
Региональный	Охватывающий экономику на уровне территории субъектов экономических районов
Национальный	Охватывающий предпринимательство на уровне макроэкономики страны ввиду неожиданных изменений в политике, законодательстве, кредитовании, налогообложении
Международный (страновой)	Связанный с изменениями в конъюнктуре мирового рынка, взаимоотношениями между странами, масштабными стихийными бедствиями
Продолжение таблицы 1
1	2	3
По сфере возникновения	Внешний	Неожиданные изменения на макроуровне в экономической политике, условиях воспроизводства, стихийных бедствий, охватывающий большие территории, валютный риск изменения конъюнктуры на мировом рынке и тому прочее
Внутренний	Риски, связанные с видами предприятия, объединения: производственные риски, криминальный риск
По возможности страхования	Страхуемый	Риск, поддающийся возможности определения его уровня и страхованию страховыми организациями, принимающими на себя риск страхователей.
Не страхуемый	Форс-мажорные риски, не поддающиеся возможности определения их уровня, а также масштабные риски, когда страхование не может принять на себя риск страхователя
По сфере активности	Финансовый	Риск на фондовом рынке: ликвидности, инфляционный и другие; банковские риски: портфельный риск, риск падения общерыночных цен, инфляции, лизинговый, факториноговый, риски, связанные со спецификой банка
Валютный	Риск колебания курсов валют
Юридический	Связанный с низким качеством законодательных актов и неожиданными изменениями в законодательстве
Производственный	Возникающий в связи с вынужденными перерывами в производстве, выходом из строя производственных факторов, несвоевременные поставки оборудования, сырья и так далее.
Конъюнктурный	Возникающий в связи с неожиданными изменениями в конъюнктуре рынка и других условий коммерческой деятельности
Продолжение таблицы 1
1	2	3
	Инвестиционный	Связанный с неопределенностями, непредвиденными обстоятельствами в инвестиционной сфере
Страховой	Риск формирования страхового фонда, управления страховым фондом, управления собственным имуществом, денежными средствами и персоналом
Криминальный	Риск социальной нестабильности
Платежа	Риск, связанный с задержками денежных расчетов
	Инновационный	Связанный с неопределенностями в инновационной сфере, начиная от выработки инновационной идеи, воплощения ее в продукте или технологии и реализации последних на рынке
По диверсифици-руемости	Систематический	В каждой сфере хозяйственной деятельности можно агрегировать определенные риски. Так, на фондовом рынке систематическим считается риск падения ценности бумаг в целом
Несистематический (специфический)	В каждой сфере деятельности можно выделить риски, связанные с опасностью нанесения ущерба или с неполучением дохода от одной операции
По степени допустимости	Минимальный	Характеризуется уровнем возможных потерь расчетной прибыли в пределах 0 – 25 %
Повышенный	Не превышающий возможных потерь прибыли в пределах 25 – 50 %
	Критический	Характеризуется уровнем возможных потерь расчетной прибыли в пределах 50 – 75 %
Недопустимый	Возможные потери близки к размеру собственных средств, вызывающих банкротство фирмы. Риск равен 75-100 %

Учитывая, что инвестиционный проект – частный случай реальных инвестиций, то в /2/ автор дает определение риска инвестиционного проекта, как вида ситуации, связанной с выбором альтернативного исхода в ходе осуществления мер и мероприятий, присущих инвестиционному проекту.

Там же автор выделяет две группы рисков, присущих инвестиционному проекту: систематический риск, который включает в себя политический, форс-мажорный, производственный и криминальный риск, и несистематический риск, включающий в себя валютный, конъюнктурный, финансовый, кредитный и риск платежа. Таким образом, общий риск инвестиционного проекта является суммой двух приведенных групп рисков.

Форс-мажорный риск связан с резким непредсказуемым и бесконтрольным изменением среды и возникновением бесконтрольных влияний, оказываемых на объект риска.

Политические риски, как правило, разделяют на четыре группы: риск национализации и экспроприации без адекватной компенсации, риск трансферта, связанный с возможными ограничениями на конвертирование местной валюты, риск разрыва контракта из-за действия властей страны, в которой находится компания, риск войны и гражданских беспорядков.

К политическим рискам относят и риски изменения налогового режима, запреты на использование кредитных карт.

Риск трансферта связан с переводами местной валюты в иностранную.

Риск разрыва контракта предусматривает ситуации, когда не помогают ни предусмотренные в договоре штрафные санкции, ни арбитраж: контракт разрывается по не зависящем от партнера причинам, в связи с изменением национального законодательства.

Риски изменения макроэкономической ситуации в основном связаны с неконтролируемой инфляцией, что приводит к непредсказуемому изменению стоимости денег и рентабельности инвестиций.

Производственный риск связан с изменением внутренней среды (факторов производства). Основные источники производственного риска – неустойчивость спроса и цен на сырье и готовую продукцию, производственный брак, уплата повышенных налогов, отчислений и штрафов.

Валютный риск связан с колебаниями курсов валют как внутри страны относительно валюты платежа, так и на международных рынках.

Финансовые риски связаны с абсолютным преобладанием кредитных договоров на короткие сроки и плавающей процентной ставкой, которую финансовые институты могут менять без согласования с заемщиком, а также низкой платежеспособной дисциплиной и длительным прохождением расчетов.

Конъюнктурные риски связаны, в частности, с непредсказуемостью изменения закупочной цены товаров, ростом издержек обращения, потерями товара при хранении и транспортировки.

Кредитные риски обусловлены возможностью невыполнения фирмой своих финансовых обязательств перед инвестором.

Риск платежа связан с задержками получения финансовых средств.

1.4 Мера риска

Как пишет автор в /7/, наиболее распространенной мерой риска коммерческого или финансового решения или операции следует считать среднеквадратическое отклонение (положительный квадратный корень из дисперсии) значения показателя эффективности этого решения или операции. Чем меньше разброс результата решения, тем более он предсказуем, то есть тем значение риска меньше.

Для оценивания риска применяются также и различные меры рассеяния: диапазон, полумежквартильный диапазон, дисперсия или вариация, полувариация, абсолютное среднее отклонение, которые подробно рассмотрены в /7/.

1.5 Методы анализа рисков

В мировой практике финансового менеджмента используются различные методы анализа рисков инвестиционных проектов. К наиболее распространенным из них следует отнести: метод корректировки нормы дисконта, анализ чувствительности критерия эффективности (чистый дисконтированный доход, внутренняя норма доходности и другие), метод сценариев, анализ вероятностных распределений потоков платежей, деревья решений, метод Монте-Карло (имитационное моделирование), метод нечетко-множественной оценки.

1.5.1 Метод корректировки нормы дисконта

Данная методика заключается в определении поправки к коэффициенту дисконтирования, учитывающей риск. Данная поправка выбирается в зависимости от характера инвестиционной деятельности. Автор в /4/ приводит пример поправок к коэффициенту дисконтирования, который показан в таблице 2.

Таблица 2 – Поправки на риск к коэффициентам дисконтирования показателей инвестиционного проекта

Уровни риска	Пример цели проекта	Премия за риск, %
Очень низкий	Вложения в государственные облигации	0
Низкий	Вложение в надежную технику	3 – 5
Средний	Увеличение объема продаж существующей продукции	8 – 10
Высокий	Производство и продвижение на рынок нового продукта	13 – 15
Очень высокий	Вложения в исследования и инновации	18 – 20

Чем выше степень рискованности проекта, тем больше значение поправки и, соответственно, меньше значение приведенной стоимости проекта и тем менее охотно инвесторы склонны вкладывать капиталы в такие проекты

В /9/ автор указывает достоинства этого метода - простота расчетов, а также в понятности и доступности. Вместе с тем, как отмечает автор, метод имеет существенные недостатки.

Метод не дает никакой информации о степени риска (возможных отклонениях результатов). При этом полученные результаты существенно зависят только от величины надбавки за риск.

Он также предполагает увеличение риска во времени с постоянным коэффициентом, что вряд ли может считаться корректным, так как для многих проектов характерно наличие рисков в начальные периоды с постепенным снижением их к концу реализации. Таким образом, прибыльные проекты, не предполагающие со временем существенного увеличения риска, могут быть оценены неверно и отклонены.

1.5.2 Анализ чувствительности

В /1/ автор описывает цель метода как сравнительный анализ влияния различных факторов инвестиционного проекта на ключевой показатель эффективности проекта, например, внутреннюю норму прибыльности.

Сначала производится выбор ключевого показателя эффективности инвестиций, в качестве которого может служить внутренняя норма прибыльности (IRR) или чистое современное значение (NPV). Далее происходит выбор факторов, относительно которых разработчик инвестиционного проекта не имеет однозначного суждения и установление их номинальных и предельных значений. Далее производится расчет ключевого показателя для всех выбранных предельных значений неопределенных факторов. В конце анализа происходит построение графика чувствительности для всех неопределенных факторов. В западном инвестиционном менеджменте этот график носит название “Spider Graph”. Данный график позволяет сделать вывод о наиболее критических факторах инвестиционного проекта, с тем чтобы в ходе его реализации обратить на эти факторы особое внимание с целью сократить риск реализации инвестиционного проекта.

В /9/ автор отмечает, что данный метод является хорошей иллюстрацией влияния отдельных исходных факторов на конечный результат проекта.

Главным недостатком данного метода, по мнению автора, является предпосылка о том, что изменение одного фактора рассматривается изолированно, тогда как на практике все экономические факторы в той или иной степени коррелированны.

1.5.3 Анализ сценариев

Это прием анализа риска, который, как отмечает автор в /1/, на ряду с базовым набором исходных данных проекта рассматривает ряд других наборов данных, которые, по мнению разработчиков проекта, могут иметь место в процессе реализации. В анализе сценария, финансовый аналитик просит технического менеджера подобрать показатели при “плохом” стечении обстоятельств (малый объем продаж, низкая цена продажи, высокая себестоимость единицы товара, и т. д.) и при “хорошем”. После этого, NPV при хороших и плохих условиях вычисляются и сравниваются с ожидаемым NPV.

В /9/ автор говорит о том, что метод позволяет получать достаточно наглядную картину для различных вариантов реализации проектов, а также предоставляет информацию о чувствительности и возможных отклонениях, а применение программных средств типа Excel позволяет значительно повысить эффективность подобного анализа путем практически неограниченного увеличения числа сценариев и введения дополнительных переменных.

1.5.4 Анализ вероятностных распределений потоков платежей

В целом применение этого метода анализа рисков, как отмечено в /9/, позволяет получить полезную информацию об ожидаемых значениях NPV и чистых поступлений, а также провести анализ их вероятностных распределений.

Вместе с тем использование этого метода предполагает, что вероятности для всех вариантов денежных поступлений известны либо могут быть точно определены. В действительности распределение вероятностей может быть задано с высокой степенью достоверности на основе анализа прошлого опыта при наличии больших объемов фактических данных. Однако чаще всего такие данные недоступны, поэтому распределения задаются, исходя из предположений экспертов, и несут в себе большую долю субъективизма.

1.5.5 Деревья решений

В /7/ дается определение дерева решений, как графического изображения последовательности решений и состояний среды с указанием соответствующих вероятностей и выигрышей для любых комбинаций альтернатив и состояний среды.

Процесс принятия решений с помощью дерева решений автор разделяет на пять этапов: формулирование задачи (то есть определение возможностей сбора информации, составление перечня событий, которые с определенной вероятностью могут произойти, установление временного порядка расположения событий и тех действий, которые можно предпринять), построение дерева решений; оценка вероятностей состояний среды (то есть сопоставление шансов возникновения конкретного события), установление выигрышей (или проигрышей), решение задачи.

Процедура принятия решения заключается в вычислении для каждой вершины дерева (при движении справа налево) ожидаемых денежных оценок, отбрасывании неперспективных ветвей и выборе ветвей, которым соответствует максимальное значение ожидаемой денежной оценки.

В /9/ автор указывает, что ограничением практического использования данного метода является исходная предпосылка о том, что проект должен иметь обозримое или разумное число вариантов развития. Метод особенно полезен в ситуациях, когда решения, принимаемые в каждый момент времени, сильно зависят от решений, принятых ранее, и в свою очередь определяют сценарии дальнейшего развития событий.

1.5.6 Имитационное моделирование (метод Монте-Карло)

Данный метод описан во многих источниках, например в /1,2,10/. Здесь в центре внимания оказываются распределения вероятностей какого-либо финансового показателя (например, NPV). В общем случае имитационное моделирование Монте-Карло - это процедура, с помощью которой математическая модель определения данного показателя подвергается ряду имитационных прогонов с помощью компьютера. В ходе процесса имитации строятся последовательные сценарии с использованием исходных данных, которые по смыслу проекта являются неопределенными, и потому в процессе анализа полагаются случайными величинами. Процесс имитации осуществляется таким образом, чтобы случайный выбор значений из определенных вероятностных распределений не нарушал существования известных или предполагаемых отношений корреляции среди переменных. Результаты имитации собираются и анализируются статистически, с тем, чтобы оценить меру риска.

Как отмечает автор в /9/, практическое применение данного метода продемонстрировало широкие возможности его использования в инвестиционном проектировании, особенно в условиях неопределённости и риска. Данный метод особенно удобен для практического применения тем, что удачно сочетается с другими экономико-статистическими методами и другими методами исследования операций. Практическое применение данного метода, как замечает автор, показало, что зачастую он даёт более оптимистичные оценки, чем другие методы, например анализ сценариев, что обусловлено перебором промежуточных вариантов.

1.5.7 Модель оценки риска стратегического инвестиционного проекта

В предыдущих разделах были проанализированы основные модели оценки эффективности инвестиционного проекта в условиях неопределенности (риска). Однако ни одна из приведенных моделей не позволяет объективно оценить риск инвестиционного проекта количественно. Эти модели оценивают риск либо путем корректировки вариационных показателей на величину риска (косвенные методы учета), либо учитывая вероятность исходов и достижений той или иной альтернативы (метод дерева решений), либо через изменение значения целевой функции при упорядочении изменения случайных величин.

В /2/ автор представляет модель оценки рисков стратегического инвестиционного проекта. Он выделяет систему критериев стратегического инвестиционного проекта, состоящую из степени неопределенности (рискованности) результата, доли покрытия заемного капитала собственным, ликвидности проекта, стратегической значимости для субъекта.

Для учета частных рисков проекта автор использует метод корректировки нормы дисконта.

В качестве целевой функции для построения модели оценки риска берется определение чистого приведенного эффекта и его классическая функция, приведенная в формуле (4).

Ненадежными случайными величинами являются чистые денежные потоки в момент времени t. На основе метода Монте-Карло определяется математическое ожидание чистого приведенного эффекта и его дисперсия.

Для оценки уровня риска проекта в качестве меры риска автор выбирает среднеквадратическое отклонение чистого приведенного эффекта от его математического ожидания. Поскольку чистый приведенный эффект – функция случайных величин денежных потоков, то его дисперсия будет зависеть от силы корреляционной связи между величинами денежных потоков для каждого периода проекта.

Среднеквадратическое отклонение чистого приведенного эффекта составит

s²(NPV) = E[NPV-E(NPV)²]

s²(NPV) = E[((α*S₁ + α²*S₂ + … +αⁿ*S_n)-( α*E(S₁) + α²*E(S₂) + … +αⁿ*E(S_n)))²], (5)

где S_i - случайная величина денежного потока, денежные единицы;

α - коэффициент дисконтирования, доли единицы

E[..] – операция вычисления математического ожидания.

Приведем формулу (5) к следующему виду

s²(NPV) = E[(α *(S₁ - E(S₁)) + α²*(S₂ - E(S₂)) +… +αⁿ*(S_n- E(S_n)))²], (6)

После преобразований, автор получает следующее выражение:

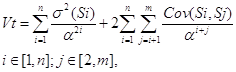(7)

где Vt - вариация (риск) проекта в момент времени t, (денежные единицы)²

n - число планово-учетных периодов проекта,

m - размер матрицы ковариаций, денежные единицы,

i,j - номер планово-учетного периода

Sij - чистые денежные потоки, денежные единицы,

s²(Si) - дисперсия случайной величины денежных потоков, (денежные единицы)²,

Cov(Si,Sj) - ковариация между величинами Si и Sj, (денежные единицы)²,

a - коэффициент дисконтирования, доли единицы.

Критерием покрытия автор называет соотношение стоимости собственного капитала субъекта в момент времени t к заемному

(8)

где Сt - критерий покрытия в момент времени t, доли единицы,

Аt - собственный капитал субъекта в момент времени t, денежные единицы,

Zt - заемный капитал в момент времени t, денежные единицы.

В случае, когда критерий покрытия меньше единицы, риск проекта резко возрастает, превышая допустимые значения. Формализация данного критерия возможно через лимитирование данного отношения. Норма лимита должна определяться экспертным путем.

Критерием, наиболее точно оценивающим стоимость инвестиционного проекта в любой учетный период, является чистый приведенный эффект. Автор предполагает, что критерий ликвидность стратегического инвестиционного проекта необходимо оценивать как отношение чистого приведенного эффекта стратегического инвестиционного проекта на один из планово-учетных периодов (кроме начального) к чистому приведенному эффекту стратегического инвестиционного проекта на начальном этапе. Этим мы получаем сверку фактических данных с прогнозируемыми. Формула для оценки ликвидности стратегического инвестиционного проекта приведена ниже

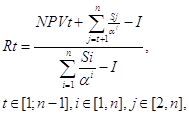
(9)

где Rt - коэффициент ликвидности в момент времени t, доли единицы,

Sij - чистые денежные потоки в i,j-й планово-учетный период, денежные единицы,

a - безрисковая ставка дисконтирования, доли единицы,

n - число планово-учетных периодов проекта,

i - номер планово-учетных периодов,

j - номер планово-учетного периода на момент реализации стратегического инвестиционного проекта,

NPVt - фактически полученная стоимость стратегического инвестиционного проекта (денежные потоки, полученные на момент времени t), денежные единицы,

I - первоначальные капиталовложения, денежные единицы.

Ясно, что Ri - случайная величина, ее реализации составляют значения коэффициента ликвидности стратегического инвестиционного проекта за плановый период.

Четвертым основным критерием стратегического инвестиционного проекта в условиях риска является стратегическая значимость. Формализация этого критерия возможна лишь при учете целей конкретного проекта.

Для рассматриваемого в работе проекта автор формирует критерий стратегической значимости для субъекта и дополняет им приведенную выше модель

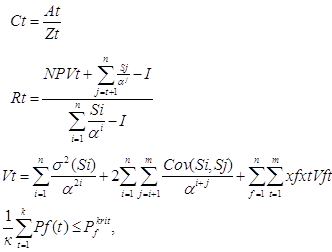
(10)

к - размерность вектора Pf(t), единицы,

f - число ресурсов в "портфеле ресурсов", единицы,

t - номер планово-учетных периода,

Pf - цена на f-й ресурс, денежные единицы,

P_t^krit - критический лимит цены на f-й ресурс, денежные единицы,

Vn - коэффициент ковариации Pf и Pt, (денежные единицы)²,

xf - доля f-го ресурса в "портфеле ресурсов", доли единицы.

1.5.8 Метод нечетко-множественной оценки инвестиционного проекта

Зададим набор нечетких чисел = (a_min, , a_max) для анализа эффективности проекта (эти числа моделируют высказывание следующего вида: "параметр А приблизительно равен и однозначно находится в диапазоне [a_min, a_max]".):

- = (I_min, , I_max) - инвестор не может точно оценить, каким объемом инвестиционных ресурсов он будет располагать на момент принятия решения;

- = (r_i _min, , r_i _max) - инвестор не может точно оценить стоимость капитала, используемого в проекте (например, соотношение собственных и заемных средств, а также процент по долгосрочным кредитам);

- = (V_min, , V_max) - инвестор прогнозирует диапазон изменения денежных результатов реализации проекта с учетом возможных колебаний цен на реализуемую продукцию, стоимости потребляемых ресурсов, условий налогообложения, влияния других факторов;

- = (G_min, , G_max) - инвестор нечетко представляет себе критерий, по которому проект может быть признан эффективным, или не до конца отдает себе отчет в том, что можно будет понимать под "эффективностью" на момент завершения инвестиционного процесса.

В том случае, если какой-либо из параметров однозначно задан, то нечеткое число вырождается в действительное число А с выполнением условия a_min = = a_max. При этом существо метода остается неизменным.

Чтобы преобразовать формулу (4) к виду, пригодному для использования нечетких исходных данных, воспользуемся способом, предложенным автором в /6/.

Зададимся фиксированным уровнем принадлежности a и определим соответствующие ему интервалы достоверности по двум нечетким числам и : [a₁, a₂] и [b₁, b₂], соответственно. Тогда основные операции с нечеткими числами сводятся к операциям с их интервалами достоверности. А операции с интервалами, в свою очередь, выражаются через операции с действительными числами - границами интервалов:

- операция "сложения"

[a₁, a₂] (+) [b₁, b₂] = [a₁ + b₁, a₂ + b₂], (11)

- операция "вычитания"

[a₁, a₂] (-) [b₁, b₂] = [a₁ - b₂, a₂ - b₁], (12)

- операция "умножения"

[a₁, a₂] (´) [b₁, b₂] = [min(a₁b₁, a₁b₂, a₂b₁, a₂b₂), max(a₁b₁, a₁b₂, a₂b₁, a₂b₂)], (13)

- операция "деления"

[a₁, a₂] (/) [b₁, b₂] = [a₁, a₂] (´) [1/b₂, 1/b₁] (14)

- операция "возведения в степень"

[a₁, a₂] (^) i = [a₁ⁱ , a₂ⁱ]. (15)

По каждому нечеткому числу в структуре исходных данных получаем интервалы достоверности [I₁, I₂], [r_i1, r_i2], [DV_i1, DV_i2]. И тогда, для заданного уровня a, путем подстановки соответствующих границ интервалов в (4) по правилам (11) - (15), получаем

(16)

Далее, задавшись приемлемым уровнем дискретизации по a на интервале принадлежности [0, 1], автор в /6/ приводит функцию принадлежности результирующего нечеткого числа к треугольному виду, ограничиваясь расчетами по значимым точкам нечетких чисел исходных данных.

Далее, исходя из функций принадлежности и конкретизируя определенный уровень принадлежности a, автор строит зону неэффективных инвестиций и вычисляет площади () этой плоской фигуры в зависимости от интервальных значений чистой приведенной стоимости (NPV₁, NPV₂ ) и критерия эффекта (G₁, G₂).

После чего, предположив, что все реализации (NPV, G) при заданном уровне принадлежности a равновозможны, автор выводит степень риска неэффективности проекта j(a) через геометрическую вероятность события попадания точки (NPV, G) в зону неэффективных инвестиций

(17)

Тогда итоговое значение степени риска неэффективности проекта он получает из уравнения (18)

(18)

В /6/ он рассматривает частный случай, когда ограничение определено четко уровнем G. С учетом формулы (18) и длинной цепи преобразований, автор получает меру оценки степени риска инвестиционных проектов, которая выглядит так

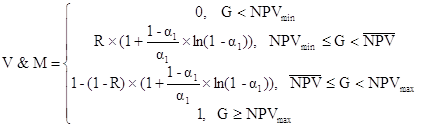, (19)

где

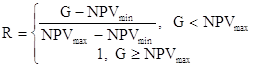, (20)

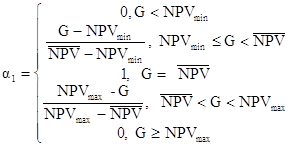(21)

Таким образом, степень риска V&M принимает значения от нуля до единицы. Каждый инвестор, исходя из своих инвестиционных предпочтений, может классифицировать значения V&M, выделив для себя отрезок неприемлемых значений риска.

В /15/ автор рассматривает полученную оценку степени риска для различных способов представлений чистого приведенного эффекта.

Результат для случая, когда критерий G представлен нечетким числом произвольного вида, представлен автором в /16/.

В работе В.В.Каблукова /2/ рассмотрена оценка риска, на основе вероятностного подхода. Риск оценивается при помощи системы критериев: критерия неопределенности, ликвидности и покрытия. Критерий неопределенности представляет собой дисперсию значений чистого приведенного эффекта. Для его расчета необходим довольно большой объем информации о входных данных, включающий в себя и распределение вероятностей, и информацию о корреляционной зависимости. Распределение задается, исходя из предположений экспертов, и несет в себе большую долю субъективизма, а для получения информации о корреляционной зависимости требует трудоемких дополнительных исследований. Выходными данными этой модели являются три критерия, значения которых необходимо сравнить между собой для получения ответа на вопрос об общем уровне риска проекта.

Метод оценки риска, разработанный Недосекиным А.О. /6/, опирается на теорию нечетких множеств. Все данные представлены нечеткими числами, а риск рассматривается как вероятность попадания значения чистого приведенного эффекта в зону неэффективных инвестиций. Чем больше эта вероятность тем, соответственно, больше риск. Это действительно так, но оценка риска может получиться односторонней, если в процессе инвестирования не учитывать во сколько раз значение заемных средств превышает собственные, а также проводить сопоставления полученных в ходе реализации проекта результаты с прогнозными.

Разработка модели, учитывающей все недостатки данных методов, является целью этой работы. Необходимо создать модель оценки уровня риска проекта, которая не опиралась бы на характер распределений входных данных, их зависимость друг от друга и учитывала бы неопределенность с различных сторон. Помимо этого модель должна давать однозначный ответ о уровне риска проекта вне зависимости от того сколько в нее входит критериев оценки.

2 Специальная часть

2.1 Описание модели оценки риска инвестиционного проекта для ОАО «Завод по производству труб большого диаметра» на основе модели риска стратегического инвестиционного проекта

Данный проект является стратегическим, поэтому для оценки его риска воспользуемся разработанной Каблуковым В.В.в /2/ моделью.

Система критериев стратегического инвестиционного проекта в данной модели состоит из: степени неопределенности (рискованности) результата, доли покрытия заемного капитала собственным, ликвидности проекта и стратегической значимости для субъекта.

Формализация четвертого критерия, по мнению Каблукова В.В., возможна лишь при учете целей конкретного проекта. В данном случае они заключаются в том, что, при осуществлении проекта исчезает необходимость закупки миллиона тонн труб за рубежом, то есть сотни миллионов долларов будут оставаться в стране и инвестироваться в промышленность и при этом будет обеспечиватся определенная независимость страны от влияний иностранных государств. Помимо этого предполагается осуществлять выпуск труб, удовлетворяющих определенным параметрам: трубы должны выдерживать температуру ниже 60 градусов, давление в 250 атмосфер и обладать крайне высокими антикоррозийными свойствами, кроме этого, они должны быть одношовными и иметь длину 18 метров.

Данные критерии довольно сложно оценить количественно. В первую очередь выполнение всех параметров влияет на себестоимость продукции. Однако по оценкам экспертов из Института по проектированию металлургических заводов (ГИПРОМЕЗ), себестоимость таких труб, выпущенных на заводе в Нижнем Тагиле, будет намного меньше цены покупки зарубежных аналогов. Без выполнения данного условия постройка завода была бы экономически невыгодна. Поэтому при разработке модели оценки рисков проекта данный критерий не учитывался.

Приведем модель оценки риска инвестиционного проекта без учета критерия стратегической значимости для субъекта:

1) Критерий для учета неопределенности (риска) стратегических инвестиционных проектов при зависимых денежных потоках

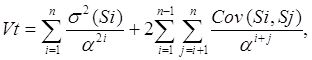
(22)

где Vt - вариация (риск) проекта в момент времени t, (денежные единицы)²

n - число планово-учетных периодов проекта,

i,j - номер планово-учетного периода

Sij - чистые денежные потоки, денежные единицы,

s²(Si) - дисперсия случайной величины денежных потоков, (денежные единицы)²,

Cov(Si,Sj) - ковариация между величинами Si и Sj, (денежные единицы)²,

a - коэффициент дисконтирования, доли единицы.

2) Критерий покрытия

(23)

где Сt - критерий покрытия в момент времени t, доли единицы,

Аt - собственный капитал субъекта в момент времени t, денежные единицы,

Zt - заемный капитал в момент времени t, денежные единицы.

3) Критерий ликвидности стратегического инвестиционного проекта

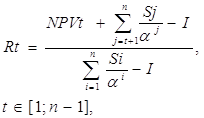(24)

где Rt - коэффициент ликвидности в момент времени t, доли единицы,

I - первоначальные капиталовложения, денежные единицы.

Ясно, что Rt - случайная величина, ее реализации составляют значения коэффициента ликвидности стратегического инвестиционного проекта за плановый период.

Проект А будет считаться выгоднее проекта В, если имеют место следующие неравенcтва:

E(NPV(A)) ≥ E(NPV(B))

Vt(A) ≤ Vt(B)

Rt(A) ≥ Rt(B), (25)

где E(NPV(A)), E(NPV(B)) - математические ожидания чистого приведенного эффекта проектов.

2.2 Проблемы, возникающие при использовании метода оценки риска инвестиционного проекта, основанном на вероятностном подходе.

Ненадежными случайными величинами являются чистые денежные потоки в момент времени t. Для каждого денежного потока необходимо задать закон распределения, формализация которого составляет основную проблему анализа, поскольку большинство проектов имеет уникальный характер, и требуют ориентировки на субъективные оценки.

При генерировании случайных чисел годовой денежный поток выступает как некое случайное число. В действительности же это совокупный показатель, включающий множество компонентов, таких как, например, эксплутационные затраты, доход от реализации продукции, инвестиции, налоги. Этот совокупный показатель изменяется не сам по себе, а с учетом изменения приведенных величин, а сами величины зависят друг от друга.

Так, например значения возмещения НДС по инвестициям и амортизация напрямую зависит от объема инвестиций, а прирост оборотных средств от эксплутационных затрат.

Наличие в модели коррелированных переменных может привести к серьезным искажениям результатов анализа риска, если эта корреляция не учитывается. Фактически наличие корреляции ограничивает случайный выбор отдельных значений для коррелированных переменных. Две коррелированные переменные моделируются так, что при случайном выборе одной из них другая выбирается не свободно, а в диапазоне , который определяется смоделированным значением первой переменной.

Довольно редко можно объективно определить точные характеристики корреляции случайных переменных в модели анализа. На практике применяют методы регрессионного анализа, который существенно затрудняет расчеты.

Еще одна сложность возникает при определении процентной ставки, учитывающей риск инвестиционного проекта. Как уже было сказано, она включает в себя безрисковую процентную ставку и так называемую надбавку за риск. Сложность заключается в том, чтобы правильно выбрать уровень риска, в определении которого приходится полагаться на субъективные оценки лица принимающего решения.

2.3 Имитационная модель получения возможных сценариев величин денежных потоков

Данная модель рассчитывает наиболее вероятные значения чистых денежных потоков для получения величин дисперсий и ковариаций последних, а также математическое ожидание чистого приведенного эффекта в момент времени t.

На первом этапе требуется определить ключевые факторы инвестиционного проекта. Например, для данной разработки это будут: доходы от реализации продукции, возмещения НДС по инвестициям, амортизация, величина инвестиций, включая НДС, прирост оборотных средств, эксплутационные затраты и налоги.

Далее необходимо определить максимальное и минимальное значение ключевых факторов и задать характер распределения вероятностей. Значение данных интервалов по всем годам проекта было выдано экспертами. За характер распределения было взято нормальное, поскольку, практика риск-анализа показывает, что в подавляющем большинстве случаев при оценки риска пользуется нормальное распределение /9/.

На основе выбранного распределения проводится имитация ключевых факторов, причем количество имитаций должно быть таким, чтобы совокупность случайных пробных значений могла считаться репрезентативной. В данном случае это количество составило 500 имитаций.

Для генерации двух случайных чисел, распределенных по нормальному закону, использовался метод Морсальи-Брея. При этом математическое ожидание высчитывалось как середина интервала разброса числа, которое было получено, как уже говорилось, от экспертов. Дисперсия рассчитывалась как середина длины отрезка данного интервала.

Из результата имитационных попыток определялись необходимые значения величин математических ожиданий и дисперсий денежных потоков для каждого периода проекта, а также их ковариации.

Математическое ожидание чистого приведенного эффекта рассчитывалось по формуле (26)

(26)

где I - первоначальные капиталовложения, денежные единицы,

N - число планово-учетных периодов проекта,

I - номер планово-учетного периода

E(Si) -математическое ожидание чистого денежного потоки в i-й учетный период проекта, денежные единицы,

к - коэффициент дисконтирования, доли единицы.

2.4 Построение модели оценки риска инвестиционного проекта при нечетких входных данных

В предложенной модели в качестве критерия для учета неопределенности (риска) стратегического инвестиционного проекта было выбрано среднеквадратическое отклонение чистого приведенного эффекта (NPV) от его математического ожидания. Если по результатам расчетов будет выявлено, что дисперсия достаточно большая, то риск того, что ожидаемое значение NPV примет запланированное значение, будет также достаточно большим.

Понятие дисперсии, так же как и математического ожидания, функции распределения и ковариации не определено для нечетких чисел, поэтому использование формулы (22) вызывает определенные трудности. В результате для учета риска была рассмотрена разработанная Недосекиным А.О. оценка возможности того, что по результатам инвестиционного процесса значение NPV окажется ниже предустановленного граничного уровня /6/. Таким образом, первый критерий оценки риска проекта будет вычисляться по следующей формуле

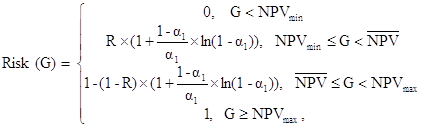(27)

где

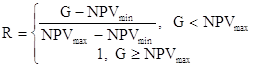, (28)

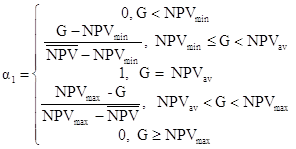. (29)

где Risk(G) – вероятность того, что значение чистого приведенного эффекта окажется ниже предустановленного граничного уровня, доли единицы,

G – уровень эффективности проекта, денежные единицы,

NPV_min – минимальное значение чистого приведенного эффекта из заданного диапазона, денежные единицы,

NPV_m_ах – максимальное значение чистого приведенного эффекта из заданного диапазона, денежные единицы,

NPV_av – среднее значение чистого приведенного эффекта из заданного диапазона, денежные единицы,

α₁ – функция принадлежности нечеткого числа NPV, доли единицы.

Степень риска Risk(G) принимает значение от 0 до 1. Каждый инвестор, исходя из своих инвестиционных предпочтений, может классифицировать значение Risk(G), выделив для себя отрезок неприемлемых значений риска. Возможна также более подробная градация степени риска, которая будет рассмотрена позже.

Формула для оценки ликвидности стратегического инвестиционного проекта, в силу введения нечетких чисел в модель и описанных в литературном обзоре операций, примет следующий вид

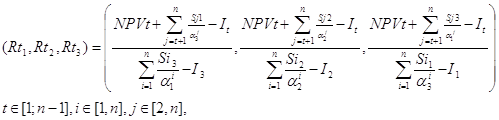
(30)

где Rt₁– минимальное значение коэффициента ликвидности в момент времени t, доли единицы,

Rt₂– среднее (наиболее ожидаемое) значение коэффициента ликвидности в момент времени t, доли единицы,

Rt₃– максимальное значение коэффициента ликвидности в момент времени t, доли единицы,

Si₁– минимальное значение чистого денежного потока в i-й планово-учетный период, денежные единицы,

Si₂– среднее значение чистого денежного потока в i-й планово-учетный период, денежные единицы,

Si₃– максимальное значение чистого денежного потока в i-й планово-учетный период, денежные единицы,

a₁ – минимальное значение безрисковой ставки дисконтирования, доли единицы,

a₂ – среднее значение безрисковой ставки дисконтирования, доли единицы,

a₃ – максимальное значение безрисковой ставки дисконтирования, доли единицы,

n – число планово-учетных периодов проекта,

I – номер планово-учетных периодов,

j – номер планово-учетного периода на момент реализации стратегического инвестиционного проекта,

I₁ –минимальное значение первоначальных капиталовложений, денежные единицы,

I₂ – максимальное значение первоначальных капиталовложений, денежные единицы,

I₃ – среднее значение первоначальных капиталовложений, денежные единицы.

Критерий покрытия в рамках данной модели оценивается по следующей формуле:

(31)

где Сt₁ – минимальное значение критерия покрытия в момент времени t, доли единицы,

Сt₂ – максимальное значение критерия покрытия в момент времени t, доли единицы,

Аt₁ - минимальное значение собственного капитала субъекта в момент времени t, денежные единицы,

Аt₂ - максимальное значение собственного капитала субъекта в момент времени t, денежные единицы,

Zt₁ - минимальное значение заемного капитала в момент времени t, денежные единицы,

Zt₂ - максимальное значение заемного капитала в момент времени t, денежные единицы.

2.5 Описание нечетко-моножественной модели принятия решения для сложных систем

Для получения однозначного ответа об уровне риска инвестиционного проекта на основе полученных данных необходимо ввести процедуру принятия решения. Такая процедура описана Смирновым А.П. в /17/.

Оператор оценивает входные данные с помощью субъективных качественных понятий типа “много”, ”мало” и т.п. Эти качественные оценки значений переменных u формализуются с помощью так называемых лингвистических переменных /11/.

Модель управления в рассматриваемом случае есть модель связи между входными переменными u и выходной переменной v. Механизм этой связи включает суждения оператора о значениях переменных. В результате на основе численного значения каждой из входных переменных оператор присваивает им качественные (нечеткие) значения. Свое решение он также принимает на основе нечеткого значения выходной переменной. Это означает, что оператор интуитивно пользуется нечеткой логикой, а конкретно – правилами нечеткого вывода.

Правила вначале формулируются с помощью термов (словесных описаний значений входных переменных). Каждое правило представляет собой текст, определяющий некоторое нечеткое отношение R между входными переменными u и выходной переменной v. Обозначим порядковый номер правила через L.

Для превращения текста правила в формальную процедуру нужно установить вид правила композиционного вывода и форму нечеткой импликации.

В качестве правила композиционного вывода для рассматриваемого класса систем может быть принята максиминная композиция, а в качестве нечеткой импликации – правило минимума (пересечение нечетких множеств предпосылки и заключения).

Нечеткое отношение R для L-го правила между j-й входной переменной u_jи выходной переменной v в соответствии с принятым правилом минимума выражено следующей функцией принадлежности

(32)

Здесь индекс i(L) означает индекс i-го терма в L-м правиле вывода. Функция принадлежности (31) отображает отношение связи между числовыми значениями в паре (u_j,v). Чем больше ее значение, тем теснее эта связь.

Результаты измерения (наблюдения) входных переменных могут быть выражены как обычными числовыми (четкими) значениями, так и качественными или размытыми значениями (нечеткими числами).

Пусть входные переменные u_j представлены нечеткими числами f_j с функциями принадлежности m_fj(u_j). Заметим, что эти функции есть результат работы системы наблюдения (измерения) в отличие от ранее введенных функций m_ji(u_j), которые выражают мнение эксперта-оператора по поводу конкретных значений u_j. Тогда в соответствии с принятым правилом композиционного вывода можно записать связь между выходной переменной v и входной переменной u_j следующим образом

(33)

Здесь M_j(v) есть функция принадлежности, устанавливающая локальную связь между нечеткой входной переменной u_j и нечеткой выходной переменной v.

Если система наблюдения дает конкретные числовые значения u_j=E_j, то формула (33) преобразуется к следующему виду

(34)

Поскольку в L-м правиле логического вывода исходные посылки связаны логическим «и» (то есть наличием данных обо всех четырех входных переменных для вывода значения выходной переменной), то соответствующая операция над нечеткими множествами реализуется в виде их пересечения. Последнее же реализуется /18/ с помощью операции минимума над соответствующими функциями принадлежности. Обозначим нечеткое множество, соответствующее выходной переменной v и полученное на основании L-го правила вывода через Q_L, а его функцию принадлежности через m_QL(v). Тогда можно записать

(35)

Данные о выходной переменной, полученные из всех правил вывода, должны быть логически объединены. Это соответствует операции максимума над функциями принадлежности /18/. Обозначив через Q результирующее нечеткое множество, соответствующее выходной переменной v, а через m_Q(v)- его функцию принадлежности, окончательно запишем

(36)

Теперь нужно оценить конкретное значение v^* для принятия решения о движении данной плавки. Эта процедура называется дефазификацией. Предложено использовать наиболее распространенный метод дефазификации /18/ – нахождение центра тяжести функции принадлежности

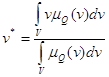(37)

Здесь V- область определения (универсальное множество) функции μ_Q(v).

Таким образом, полученная модель использует входные переменныe u_j, имеющие четкие значения, и выдает выходную переменную v также в четком виде., в то время как внутренняя структура модели является нечеткой.

2.6 Описание нечетких данных для модели принятия решения о риске инвестиционного проекта

В качестве входной информации (входных переменных модели) выступают следующие параметры: оценка риска проекта по первому критерию (вероятность попадания в зону неэффективности), оценка риска проекта по второму критерию (критерий ликвидности), оценка риска по третьему критерию (критерий покрытия).

Качественные оценки этих критериев формализуются с помощью лингвистических переменных А₁, А₂, А₃ соответственно.

Лингвистическая переменная A_j(j=1,3) характеризуется следующим набором

<A_j,T(A_j),U_j>, (38)

где A_j – название переменной,

T(A_j) – множество значений переменной (множество термов),

U_j – универсальное множество соответствующей базовой переменной u_j.

Ниже приведены значения компонент указанного набора:

- A₁=”Уровень риска для первого критерия”, T(A₁)=”минимальный, повышенный, критический, недопустимый”.

- A₂=”Уровень риска для второго критерия”, T(A₂)=”минимальный, повышенный, критический, недопустимый”.

- A₃=” Уровень риска для третьего критерия ”, T(A₃)=” минимальный, повышенный, критический, недопустимый ”.

Такая градация степени риска взята из классификации рисков Каблукова В.В., где он описывает данные категории следующим образом: минимальная степень допустимости риска характеризуется уровнем возможных потерь расчетной прибыли в пределах 0 – 25 %, повышенная степень – 25 – 50 %, критическая - 50 – 70 %, недопустимая – 75 – 100 %.

Каждому множеству T(A_j) соответствуют четыре терма T_ji(A_j).

Каждый терм T_ji(A_j) (i=1,4) характеризуется функцией принадлежности m_ji(u_j), которая определена на соответствующем универсальном множестве U_j и выражает смысл данного терма.

Опишем сформированные функции принадлежности для первого критерия оценки риска. Здесь К₁, К₂, К₃ – границы интервалов для соответствующих уровней риска. Границей для недопустимого уровня является единица. Значения данных интервалов можно получить из экспертного опроса.

Минимальный уровень риска для первого критерия

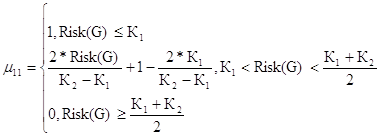(39)

Повышенный уровень риска для первого критерия

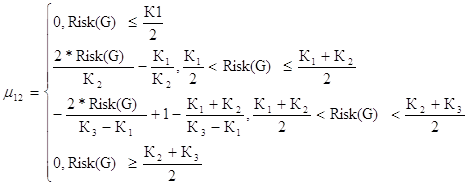(40)

Критический уровень риска для первого критерия

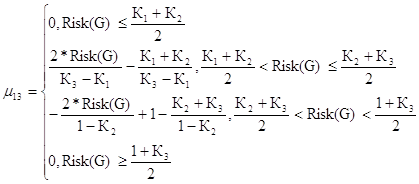(41)

Недопустимый уровень риска для первого критерия

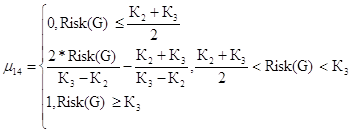(42)

Опишем функции принадлежности к риску для критерия ликвидности. Тут тоже используются границы интервалов для соответствующих уровней риска К₁, К₂, К_3. Где К₁ – это граница недопустимого уровня риска, К₂ – критического, К₃ – повышенного, границей минимального уровня является единица. Значения данных интервалов можно получить из экспертного опроса.

Поскольку в результате расчетов мы получаем три значения коэффициента, которые характеризуют минимальное (Rt₁), среднее (наиболее ожидаемое) (Rt₂) и максимальное значение (Rt₃) критерия, то для свертки этих значений воспользуемся следующей формулой

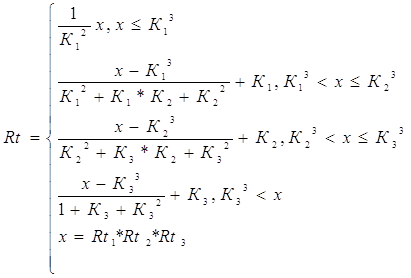(43)

Сформируем функции принадлежности коэффициента ликвидности к введенной лингвистической переменной:

Минимальный уровень риска для второго критерия

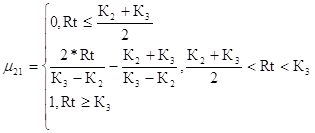(44)

Повышенный уровень риска для второго критерия

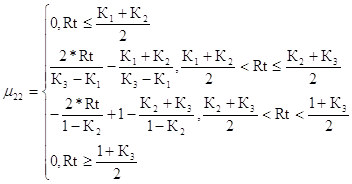(45)

Критический уровень риска для второго критерия

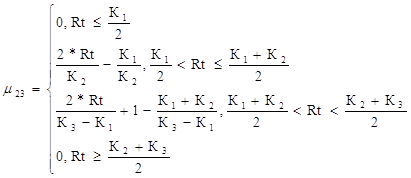(46)

Недопустимый уровень риска для второго критерия

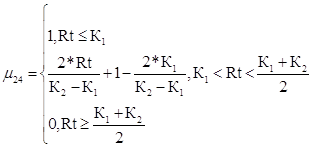(47)

Опишем функции принадлежности для критерия покрытия. Тут также используются границы интервалов для соответствующих уровней риска К₁, К₂, К_3, где К₁ – это граница недопустимого уровня риска, К₂ – критического, К₃ – повышенного. Границей минимального уровня является единица. Значения данных интервалов можно получить из экспертного опроса.

Поскольку в результате расчетов мы получаем два значения, которые характеризуют минимальное (Сt₁) и максимальное значение (Ct₂) критерия, то для свертки этих значений воспользуемся следующей формулой

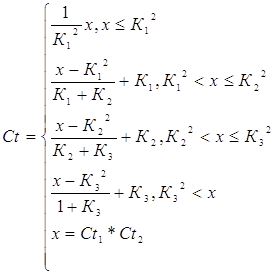(48)

Сформируем функции принадлежности коэффициента покрытия к введенной лингвистической переменной. Минимальный уровень риска для третьего критерия

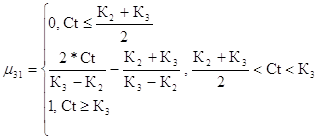(49)

Повышенный уровень риска для третьего критерия

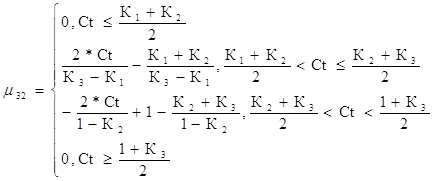(50)

Критический уровень риска для третьего критерия

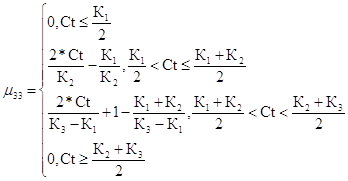(51)

Недопустимый уровень риска для третьего критерия

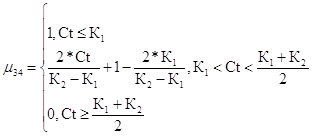(52)

Определим теперь описание выходной переменной – уровня риска инвестиционного проекта. Это лингвистическая переменная B, которая характеризуется также набором, подобным предыдущему

<B,T(B),V>, (53)

где B – название переменной (B = «Уровень риска проекта»);

T(B) – множество термов (T(B) = «минимальный», «повышенный», «критический», «недопустимый»);

V – универсальное множество базовой переменной v (в долях единицы).

Значения функции принадлежности m_k (v) термов T_k(B) (k=1,4) также могут быть получены из экспертной информации.

Сформируем функции принадлежности риска проекта к введенной лингвистической переменной. Здесь К₁, К₂, К₃ – границы интервалов для соответствующих уровней риска. Границей для недопустимого уровня является единица. Значения данных интервалов можно получить из экспертного опроса. Минимальный уровень риска проекта

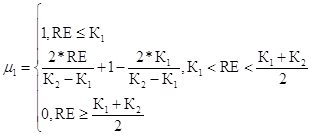, (54)

где RE – уровень риска инвестиционного проекта, (доли единицы).

Повышенный уровень риска для первого критерия

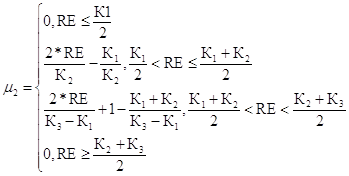(55)

Критический уровень риска для первого критерия

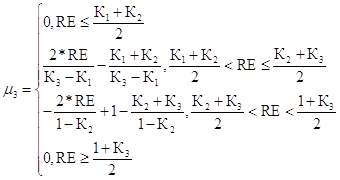(56)

Недопустимый уровень риска для первого критерия

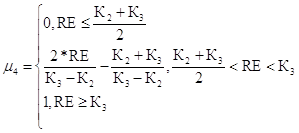(57)

Смысл нечеткого вывода состоит в следующем. Если А - причина (предпосылка), а В- результат (заключение), то можно определить нечеткое отношение R соответствия между А и В, смысл которого отражается в знании: из А скорее всего следует В. Это знание выражено формулой R=А®В( где ® это символ нечеткой импликации). Тогда связь между нечеткой предпосылкой А’ и нечетким заключением В’ можно записать в виде

B’ = A’ · R = A’· (A®B), (58)

где значок · - это правило композиционного вывода (правило свертки).

В рассматриваемой логической системе предпосылки определяются лингвистическими переменными А₁,А₂,А₃, а заключение – лингвистической переменной В. В каждом конкретном правиле имеются три предпосылки (по числу входных переменных) и одно заключение. Каждое такое логическое правило определяет одно из возможных состояний объекта управления, а полный набор правил характеризует все возможные состояния /17/. Поскольку каждая из трех предпосылок имеет четыре значения соответствующей лингвистической переменной, а в правилах вывода должны присутствовать все комбинации значений, то общее число правил равно 4³ =64.

В виде термов одно из этих правил может быть написано следующим образом: если уровень риска для первого критерия - минимальный, уровень риска для второго критерия - минимальный, уровень риска для третьего критерия - минимальный, то уровень риска проекта – минимальный.

3 Анализ результатов

3.1 Обоснование выбора среды программирования

Программа была написана в Delphi 7.0. Эта среда является средой разработки, которая использует многие идеи и концепции, заложенные в графическом интерфейсе пользователя Windows. Delphi предоставляет широкие возможности управления приложениями.

Delphi обладает широким набором возможностей, начиная от проектировщика форм и кончая поддержкой всех форматов популярных баз данных.

Характерные черты Delphi:

- многократно используемые и расширяемые компоненты, отсутствие необходимости программировать такие компоненты Windows общего назначения, как метки, пиктограммы, диалоговые панели управления.

- встроенные шаблоны форм и приложений, которые можно использовать для быстрой разработки собственных прикладных программ.

- настройка среды разработки в виде палитры компонентов, редактора кода, шаблонов приложений и форм, настраиваемых по желанию программиста.

- широкие возможности доступа к данным.

3.2. Описание программы

Программа «Оценка риска инвестиционного проекта» анализирует степень риска проекта и выдает результат о его уровне в долевом отношении.

Риск инвестиционного проекта оценивается на основе трех показателей: вероятности попадания в зону неэффективности инвестиций, критерия покрытия и критерия ликвидности, которые были описан выше.

Программа реализует следующие основные функции: ввод и коррекцию исходных данных в интерактивном режиме, формирование денежных потоков, оценку риска инвестиционного проекта на основе вероятностного или нечетко-множественного подхода, предоставление окончательных результатов в виде отчета.

Рассмотрим основные элементы пользовательского интерфейса. Структура начального окна программы изображена на рисунке А1 приложения А.

Таким образом, программа включает в себя два основных этапа: оценка риска, основанная на вероятностном подходе и оценка риска при нечетких входных данных.

Первый этап предполагает ввод исходной информации в следующие таблицы: значение коэффициента дисконтирования, значение величин собственного и заемного капитала субъекта, прогнозируемые чистые денежные потоки, чистые денежные потоки, полученные в ходе реализации инвестиционного проекта, матрица ковариаций случайных величин денежных потоков, а также значение первоначальных денежных капиталовложений. Диалоговое окно ввода информации во все перечисленные выше таблицы представлено на рисунке А2 приложения А.

Главное меню данного окна содержит опции: файл, рассчитать. Опция «файл» содержит в себе процедуры сохранения введенных данных и открытия файла данных, а опция «рассчитать» - пункты формирование денежных потоков и анализ результатов.

При выборе пункта формирование денежных потоков появляется окно, изображенное на рисунке А3 приложения А.

Данная форма предполагает ввод информации о случайных составляющих проекта для формирования их возможных значений. Все введенные данные можно сохранить, выбрав соответствующую опцию в меню файл. Также предполагается и автоматический ввод информации при активизации опции «открыть» меню файл.

При загрузке формы «Формирование денежных потоков» в таблицы «Поступление денежных средств» и «Расход денежных средств» включены названия некоторых предполагаемых составляющих, которые можно по желанию изменить, удалить или добавить новые, выбрав в меню «Правка» соответствующие опции.

Опция меню «Сформировать» на основе исходных данных об интервалах значений случайных составляющих денежного потока проводит имитации возможных сценариев и рассчитывает такие величины как математическое ожидание, дисперсия и ковариация чистых денежных потоков при нормальном распределении случайных величин. Все результаты имитации помещаются в соответствующие таблицы предыдущего окна, а описываемое окно автоматически закрывается.

При выборе опции «Анализ результатов», находящейся в пункте меню «Рассчитать» основного окна «Оценка риска проекта на основе вероятностного подхода» происходит анализ введенной информации и рассчитываются значения трех показателей для каждого периода проекта. Эти данные помещаются в таблицу результатов, находящуюся на форме «Анализ результатов». Данная форма показана на рисунке А4 приложения А.

При начальном выборе метода оценки риска инвестиционного проекта на основе нечетко-множественного подхода загружается окно, показанное на рисунке А5 приложения А.

Данная форма предполагает ввод исходной информации в следующие таблицы: интервалы значений коэффициентов дисконтирования, интервалы значений величин собственного и заемного капитала субъекта для каждого планово-учетного периода, интервалы чистых денежных потоков, а также интервал значения первоначальных денежных капиталовложений.

Главное меню показанного окна содержит опции: файл и данные. Опция «файл» содержит в себе процедуры сохранения введенных данных и открытия файла данных, а опция «данные» - пункты: формирование денежных потоков, коэффициент ликвидности, анализ риска проекта, формирование уровней риска, формирование правил вывода.

При выборе пункта меню «Формирование денежных потоков» появляется окно, аналогичное изображенному на рисунке А3 приложения А.

Данный пункт помогает рассчитать значения конечных интервалов чистых денежных потоков при входных нечетких данных. Он предполагает ввод информации об интервалах составляющих денежного потока.

Опция меню «Сформировать» данного окна на основе исходных данных о интервалах значений составляющих денежного потока делает расчет конечных интервалов денежного потока для каждого периода проекта и помещает результаты в соответствующие таблицы предыдущего окна, а описываемое окно автоматически закрывается.

При выборе опции «Коэффициент ликвидности», находящейся в пункте меню «Данные» основного окна «Оценка риска проекта» появляется окно, показанное на рисунке А6 приложения А.

Если данная опция не была выбрана, то учет риска проекта происходит только по двум критериям. При вводе же соответствующей информации в таблицы: коэффициенты дисконтирования, полученные значения чистых денежных потоков, а также величины первоначальных капиталовложений, учет риска производится на основе трех критериев.

При выборе опции «Формирование уровней риска» появляется окно, показанное на рисунке А7 приложения А.

Данная форма предполагает ввод значений границ интервалов, которые соответствуют различным уровням риска для каждого критерия.

При выборе опции «Формирование правил вывода» появляется окно, показанное на рисунке А8 приложения А.

Данная форма предполагает ввод таблицы правил вывода. Первоначально предлагается уже составленная таблица. По желанию ее можно изменить. Данные внутри таблицы означают: м – уровень конечного риска проекта минимальный, п – повышенный, к – критический, н – недопустимый.

При выборе опции «Расчет риска проекта» происходит анализ введенной информации, рассчитываются значения показателей для каждого периода проекта, и делается вывод об уровне риска. Конечный результат появляется на нижней панели окна. Если необходима более подробная информация, то нужно нажать кнопку «Отчет».

При нажатии этой кнопки загружается форма отчета, показанная на рисунке А9 приложения А. Текст программы приведен в приложение Б.

3.3 Оценка риска инвестиционного проекта ОАО «Завод по производству труб большого диаметра» с применением теории вероятностей

Исходные данные для проведения оценки риска инвестиционного проекта были предоставлены институтом по проектированию металлургических заводов (ГИПРОМЕЗ).

Для расчета значения критерия покрытия были взяты данные из таблицы 3.

Таблица 3 – Схема финансирования строительства завода по производству труб большого диаметра, %

Источники финансирования	Периоды проекта, года
4	5	6	7	8	9	10	11	12
Собственные средства – акционерный капитал	31,3	41,0	36,6	35,0	48,0	61,0	74,0	87,0	100
Заемные средства	68,7	59,0	63,4	65,0	52,0	39,0	26,0	13,0	0

Поскольку оказалось достаточно трудно оценить интервалы разбросов чистых денежных потоков, то для его формирования были использованы составляющие, представленные в таблице 4.

Сначала производилась оценка риска проекта на основе вероятностного подхода. Для этого при помощи программы были рассчитаны математическое ожидание, дисперсия и ковариация денежного потока для каждого периода проекта. Значения первого представлены в таблице 4, а последних двух величин - в таблице В1 приложения В. В данной таблице дисперсии находятся на главной диагонали.

Расчет риска проекта начали с четвертого года, а за первоначальные капиталовложения приняли среднюю сумму вложений на строительство завода, требуемую за три первых года с начала строительства, то есть I равнялось 17020 миллионов рублей. Норма дисконта была равна 10 %.

Значения критериев неопределенности (Vt), ликвидности (Rt) и покрытия (Ct), а также чистого приведенного эффекта (NPVt) для каждого планово-учетного периода проекта, рассчитанные программой, показаны в таблице 5.

Таблица 4 – Потоки финансовых средств для оценки риска проекта, млн.руб.

Название составляющих	Планово-учетные периоды проекта, года
1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Поступление денежных средств
Доходы от реализации продукции	0	0	0	9333	15484	15824	15824	15824	15824	15824	15824	15824	15824	15824	15824
0	0	0	11541	19146	19567	19567	19567	19567	19567	19567	19567	19567	19567	19567
Возмещение НДС по инвестициям	0	0	0	2116	2039	0	0	0	0	0	0	0	0	0	0
0	0	0	2539	2447	0	0	0	0	0	0	0	0	0	0
Амортизация	0	0	0	1012	1778	1778	1778	1778	1778	1778	1778	1778	1778	1778	1778
0	0	0	1214	2134	2134	2134	2134	2134	2134	2134	2134	2134	2134	2134
Расход денежных средств
Инвестиции, включая НДС	3353	4320	9347	7907	0	0	0	0	0	0	0	0	0	0	0
4024	5184	11216	9488	0	0	0	0	0	0	0	0	0	0	0
Прирост оборотных средств	0	0	0	630	235	12	0	0	0	0	0	0	0	0	0
0	0	0	696	260	14	0	0	0	0	0	0	0	0	0
Эксплутационные затраты	0	0	0	6302	8656	8775	8775	8775	8775	8775	8775	8775	8775	8775	8775
0	0	0	6966	9568	9699	9699	9699	9699	9699	9699	9699	9699	9699	9699
Налоги	0	0	0	916	1906	1934	1910	1886	1861	1837	1813	1788	1764	1740	1715
0	0	0	1120	2330	2364	2334	2305	2275	2245	2215	2186	2156	2126	2097
Математическое ожидание	-3353	-4320	-9347	-1319	1053	8156	8107	8235	8115	8151	8255	8374	8502	8256	8426

Таблица 5 – Результат оценки риска инвестиционного проекта на основе вероятностного подхода,

Период проекта	Ct, доли единицы	NPVt, млрд. руб.	Vt, (млрд. руб.)²	σ², млрд. руб.
1	2	3	4	5
4	0,58	-14,54	660,89	0,81
5	0,92	-8,24	1878,80	1,37
6	1,56	-3,63	2952,54	1,72
7	2,85	0,53	3784,71	1,94
8	6,69	4,37	4832,95	2,20
9	100,00	7,81	5846,83	2,42
10	100,00	10,95	6698,38	2,59
11	100,00	13,84	7286,51	2,70
12	100,00	16,51	7583,38	2,76
13	100,00	18,98	7693,57	2,77
14	100,00	21,15	8045,46	2,84
15	100,00	23,17	8373,56	2,89

Так как критерий неопределенности представляет собой дисперсию чистого приведенного эффекта, то для простоты восприятия в таблицу курсовые - 700 р.
Работы, похожие на Дипломная работа: Разработка инвестиционного проекта ОАО "Завод по производству труб большого диаметра"

Расчет стоимости пластиковых оконных конструкций и дверей

Министерство образования и науки Российской Федерации Федеральное агентство по образованию Государственное образование учреждения "Оренбургский ...
if msg1.Sender.Hint='1' then begin p:=pos('#Глухой',nam);delete(nam,p,7);msg1.Sender.Destroy;end;
begin datetimepicker1.Date:=Date;end;end.

Раздел: Рефераты по информатике, программированию
Тип: курсовая работа

Основы дискретной математики
Федеральное агентство по образованию Новомосковский институт (филиал) Государственного образовательного учреждения высшего профессионального ... if a[j]<x then begin k:=j; x:=a[k] end;a[k]:=a[i]; a[i]: =xend; stringgrid1.cells [i, 0]:=inttostr(i); end;	Раздел: Рефераты по информатике, программированию Тип: учебное пособие

Файловая оболочка (Delphi 30 )
Постановка задачи. Задача заключается в разработке файловой оболочки для операционной системы Windows"95/98. В программе реализовать механизмы ... if not(((FileDateTime(CurDir+F.Name) FindForm.DateIsAfter.Date))) then Continue; if (MaskR[j]=FR[i]) and (MaskR[j]<>'') then*	Раздел: Рефераты по информатике, программированию Тип: реферат

Object Pascal

1. Основы языка Object Pascal 1.1. Алфавит языка Основными символами языка Object Pascal являются: - символы _ - 26 больших и 26 малых латинских букв ...
if ( z[i, j] > 0) then s:= s + z [i, j];
... R с целью сокращения времени вычислений) и оператор внутреннего цикла со счетчиком j. Поскольку наружный цикл в своем теле содержит несколько операторов, то они заключены в ...

Раздел: Рефераты по информатике, программированию
Тип: реферат

Разработка баз данных в Delphi
Создание баз данных в Delphi Урок 1: Настройка BDE Содержание урока 1: Обзор 2 Сущность BDE 2 Алиасы 2 Системная информация утилиты настройки BDE 4 ... procedure TForm1.NextClick(Sender: if DataSource1.DataSet.State = dsBrowse then begin	Раздел: Рефераты по информатике, программированию Тип: реферат

5rik.ru

Материалы для учебы и работы

Дипломная работа: Разработка инвестиционного проекта ОАО "Завод по производству труб большого диаметра"

1.1 Основные понятия инвестиционного проектирования

1.1.1 Понятие проекта и проектного цикла

1.1.2 Оценка текущей стоимости денег

1.1.3 Общая характеристика методов оценки эффективности инвестиционного проекта

1.2 Общие понятия неопределенности и риска

1.3 Виды рисков

1.4 Мера риска

1.5 Методы анализа рисков

1.5.1 Метод корректировки нормы дисконта

1.5.2 Анализ чувствительности

1.5.3 Анализ сценариев

1.5.4 Анализ вероятностных распределений потоков платежей

1.5.5 Деревья решений

1.5.6 Имитационное моделирование (метод Монте-Карло)

1.5.7 Модель оценки риска стратегического инвестиционного проекта

1.5.8 Метод нечетко-множественной оценки инвестиционного проекта

2.2 Проблемы, возникающие при использовании метода оценки риска инвестиционного проекта, основанном на вероятностном подходе.

2.3 Имитационная модель получения возможных сценариев величин денежных потоков

2.4 Построение модели оценки риска инвестиционного проекта при нечетких входных данных

2.5 Описание нечетко-моножественной модели принятия решения для сложных систем

2.6 Описание нечетких данных для модели принятия решения о риске инвестиционного проекта

3.1 Обоснование выбора среды программирования

3.2. Описание программы

3.3 Оценка риска инвестиционного проекта ОАО «Завод по производству труб большого диаметра» с применением теории вероятностей