Контрольная работа: Расчет статистических показателей
Министерство образования и науки Украины
Донбасская государственная машиностроительная академия
Контрольная работа по дисциплине "Статистика"
Студента гр. ПВ09-1з Измайлова А.О.
Зачетная книжка №095011
Вариант №11
Краматорск 2010
Задача 1.12
Имеются данные о стаже работы и средней месячной заработной плате рабочих (таблица 1). Для выявления зависимости между стажем работы и месячной заработной платой сгруппируйте рабочих по числу лет стажа, образовав пять групп с равными интервалами. По каждой группе и в целом по совокупности рабочих подсчитайте:
1) число рабочих;
2) среднюю заработную плату;
3) средний возраст.
Решение
Таблица 1
| Рабочий | Возраст лет | Месячная зарплата, грн. |
| 1 | 25 | 280 |
| 2 | 24 | 310 |
| 3 | 46 | 490 |
| 4 | 45 | 420 |
| 5 | 42 | 360 |
| 6 | 50 | 410 |
| 7 | 29 | 340 |
| 8 | 36 | 390 |
| 9 | 54 | 490 |
| 10 | 29 | 350 |
| 11 | 18 | 200 |
| 12 | 37 | 380 |
| 13 | 25 | 290 |
| 14 | 30 | 320 |
| 15 | 26 | 310 |
| 16 | 36 | 400 |
| 17 | 40 | 430 |
| 18 | 28 | 340 |
| 19 | 35 | 380 |
| 20 | 25 | 380 |
Вычислим величину интервала группировочного признака (возраста) по формуле:
![]()
где xmax – наибольшее значение признака,
xmin – наименьшее значение признака,
n – число образованных групп (по условию 5).
Имеем:
i=(54-18)/5= 7.2 года
Следовательно, первая группа рабочих имеет возраст 18-25,2 года, вторая – 25,2-32,4 лет, третья – 32,4-39,6 лет, четвертая – 39,6-46,8 лет, пятая – 46,8-54 лет возраста. По каждой группе подсчитаем численность рабочих и оформим результаты в виде рабочей таблицы 2.
Таблица 2
| № группы | Группа рабочих по возрасту, лет | возраст, лет | Месячная зарплата, грн. |
| I | 18-25,2 | 18,0 | 200,0 |
| 24,0 | 310,0 | ||
| 25,0 | 280,0 | ||
| 25 | 380 | ||
| 25 | 290 | ||
| Итого по I группе: | 23,4 | 292,0 | |
| II | 25,2-32,4 | 26 | 310 |
| 28 | 340 | ||
| 29 | 350 | ||
| 29 | 340 | ||
| 30 | 320 | ||
| Итого по II группе: | 28,4 | 332,0 | |
| III | 32,4-39,6 | 35 | 380 |
| 36 | 400 | ||
| 36 | 390 | ||
| 37 | 380 | ||
| Итого по III группе: | 36,0 | 387,5 | |
| IV | 39,6-46,8 | 40 | 430 |
| 42 | 360 | ||
| 45 | 420 | ||
| 46 | 490 | ||
| Итого по IV группе: | 43,3 | 425,0 | |
| V | 46,8-54 | 50 | 410 |
| 54 | 490 | ||
| Итого по V группе: | 52,0 | 450,0 |
Построим аналитическую таблицу по группировочному признаку (см. таблицу 3)
Таблица 3
| № группы | Группа рабочих по стажу, лет | Число рабочих, чел. | Возраст, лет | Месячная зарплата, грн. | ||
| всего | Средний по группе | Всего | Средняя по группе | |||
| I | 18-25,2 | 5 | 117,0 | 23,4 | 1460,0 | 292,00 |
| II | 25,2-32,4 | 5 | 142,0 | 28,4 | 1660,0 | 332,00 |
| III | 32,4-39,6 | 4 | 144,0 | 36,0 | 1550,0 | 387,50 |
| IV | 39,6-46,8 | 4 | 173,0 | 43,3 | 1700,0 | 425,00 |
| V | 46,8-54 | 2 | 104,0 | 52,0 | 900,0 | 450,00 |
| Всего: | 20 | 576,0 | 36,6 | 7270,0 | 377,3 |
Общий возраст рабочих равен 576 лет (сумма возрастов всех 20-ти рабочих), общая месячная зарплата – 7270 грн. (сумма месячных зарплат всех 20-ти рабочих), средний возраст в целом по совокупности рабочих равен 183,1/20=36,6 лет, соответственно, средняя зарплата в целом по совокупности равна 1886,5/20=377,3 грн.
Построим гистограмму распределения (см. рисунок 1).
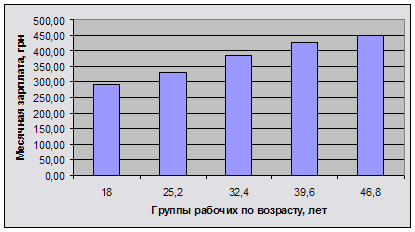
Рисунок 1 – Гистограмма распределения
Вывод: результаты группировки представлены в таблице 3, они свидетельствуют о том, что с увеличением возраста работы средняя месячная заработная плата увеличивается, то есть между возрастом рабочего и месячной заработной платой существует прямая зависимость. Общее число рабочих – 20 человек, средний возраст в целом по совокупности рабочих равен 36,6 года, средняя месячная зарплата по совокупности рабочих – 377,3 грн. Данные по каждое группе представлены в таблице 3.
Задача 2.13
Имеются данные о распределении заводов области по уровню коэффициента сменности (таблица 4).
Таблица 4
| № п/п | Группа предприятий по уровню коэффициента сменности работы оборудования | Число единиц оборудования, % |
| 1 | До 1,7 | 2,2 |
| 2 | 1,7-1,8 | 12,8 |
| 3 | 1,8-1,9 | 32,6 |
| 4 | 1,9-2,0 | 24,9 |
| 5 | 2,0-2,1 | 23,4 |
| 6 | 2,1-2,2 | 4,1 |
| Итого | 100,0 |
Определить средний уровень коэффициента сменности по области:
Решение
Согласно условию, имеем:
1) Определим моду:
![]() =
=![]() =1,813
=1,813
2) Определим медиану:
![]() =
=![]() =1,853
=1,853
Вывод: Средний уровень сменности по области составил 1,853.
Задача 3.16
Для изучения качества электроламп проведено выборочное обследование. В случайном порядке из 10000 ламп отобрано 100 штук. Распределение ламп по времени горения представлено в таблице 5. На основании данных вычислите:
1) Среднее время горения электрических ламп;
2) Моду и медиану;
3) Дисперсию и среднее квадратическое отклонение;
4) коэффициент вариации;
5) с вероятностью 0,954 предельную ошибку выборки и границы, в которых можно ожидать среднее время горения всех ламп.
6) С вероятностью 0,954 границы удельного веса ламп с пределом горения свыше 5000 ч.
Решение
Таблица 5
| Время горения, ч. | до 3000 | 3000-3500 | 3500-4000 | 4000-4500 | 4500-5000 | 5000-5500 | 5500-6000 |
| Число ламп, шт. | 5 | 7 | 8 | 30 | 25 | 14 | 11 |
Решение
Способ моментов основан на применении математических свойств средней арифметической взвешенной и позволяет значительно упростить технику вычисления. Расчет производится по формуле
![]() ,
,
где ![]() - момент первого порядка,
- момент первого порядка,
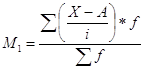
i – величина интервала (шаг),
A – постоянная величина, на которую уменьшаются все значения признака. В вариационных рядах с равными интервалами в качестве такой величины принимается вариант ряда, с наибольшей частотой.
Построим рабочую таблицу (см. таблицу 6).
Имеем
I24, A=4250 (при f max=30)
Таблица 6
| Время горения ч. | Число ламп шт. | Середина интервала, X |
|
|
|
|
| до 3000 | 5 | 2750 | -1500 | -3 | -15 | 45 |
| 3000-3500 | 7 | 3250 | -1000 | -2 | -14 | 28 |
| 3500-4000 | 8 | 3750 | -500 | -1 | -8 | 8 |
| 4000-4500 | 30 | 4250 | 0 | 0 | 0 | 0 |
| 4500-5000 | 25 | 4750 | 500 | 1 | 25 | 25 |
| 5000-5500 | 14 | 5250 | 1000 | 2 | 28 | 56 |
| 5500-6000 | 11 | 5750 | 1500 | 3 | 33 | 99 |
| Итого: | 100 | 0 | 49 | 261 |
Определим момент первого порядка
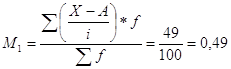
Определим момент второго порядка
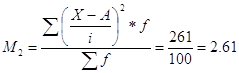
Тогда имеем средняя продолжительность горения электрических ламп:
![]()
Определим моду:
![]() =
=![]() =4907
ч.
=4907
ч.
Определим медиану:
![]() =
=![]() =4833
ч.
=4833
ч.
Дисперсия определим по формуле:
![]()
Среднее квадратическое отклонение определим по формуле:
![]()
Коэффициент вариации:
![]()
Так как коэффициент вариации меньше 33% , значит ряд устойчивый (совокупность однородная).
Рассчитаем предельную ошибку выборки:
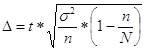
где t - коэффициент доверия,
n – количество единиц выборочной совокупности,
N – количество единиц генеральной совокупности
При вероятности Р=0,954 коэффициент доверия равен t =2,
n=100, определим N:
по условию выборка 5%я, тогда
![]()
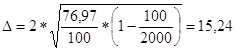 =
=
= 2*((76.97^2/100)*(1-100/2000))^0.5=15,24
Пределы :
![]()
![]()
4479,76£4495£4510,24
С вероятностью 0,954 границы удельного веса ламп с пределом горения свыше 5000 ч.
Рассчитаем предельную ошибку выборки:
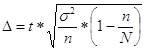
где t - коэффициент доверия,
n – количество единиц выборочной совокупности,
N – количество единиц генеральной совокупности
При вероятности Р=0,954 коэффициент доверия равен t =2,
n=25, определим N:
по условию выборка 5%я, тогда
![]() =25*100/5=500
=25*100/5=500
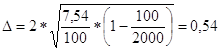 = 2*((76.97^2/25)*(1-25/500))^0.5=30
= 2*((76.97^2/25)*(1-25/500))^0.5=30
Пределы:
![]()
![]()
4465£4495£4525
Ответ: средняя длительность горения ламп 4495 ч.; дисперсия - 5924.75, среднее квадратическое отклонение - 76.97 ч.; коэффициент вариации -1.71%;
предельная ошибка выборки – 15,24 ч.; границы, в которых можно ожидать среднюю длительность горения ламп по всей выборке: 4479,76£4495£4510,24.
предельная ошибка выборки – 30 ч.; границы, в которых можно ожидать среднюю длительность горения ламп более 5000 ч.: 4465£4495£4525.
Задача 4.17
Урожайность пшеницы в области характеризуется данными см. таблицу 7
Таблица 7
| Год | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 |
| Средняя урожайность ц/га | 32 | 40 | 45 | 48 | 49 | 51 |
Для анализа ряда динамики исчислите:
1) абсолютный прирост, темпы роста и прироста (базисные и цепные), абсолютное содержание одного процента прироста (полученные показатели представьте в виде таблицы);
2) среднегодовую урожайность пшеницы;
3) среднегодовой абсолютный прирост урожайности пшеницы;
4) среднегодовой темп роста и прироста с 1994г. по 1999 г., с 1995г. по 1999г.
Изобразите исходные данные графически. Сделайте выводы.
Решение
1) Абсолютный прирост
базисный ![]() определяется по формуле:
определяется по формуле:
![]() ,
,
где ![]() - уровни i-го и базисного годов соответственно;
- уровни i-го и базисного годов соответственно;
Абсолютный прирост цепной
(по годам) ![]() определяется по формуле:
определяется по формуле:
![]() ,
,
где ![]() - уровень предыдущего года;
- уровень предыдущего года;
Темп роста базисный ![]() определяется по формуле:
определяется по формуле:
![]() ,
,
Темп роста цепной (по
годам) ![]() определяется по формуле:
определяется по формуле:
![]()
Темп прироста базисный ![]() определяется по формуле:
определяется по формуле:
![]()
Темп прироста цепной (по
годам) ![]() определяется по формуле:
определяется по формуле:
![]()
Абсолютное содержание
одного процента прироста ![]() определяется по формуле:
определяется по формуле:
![]()
Рассчитаем по перечисленные величины и составим рабочую таблицу (см. таблица 8).
Таблица 8
| Год | 1994 | 1995 | 1996 | 1997 | 1998 | 1999 |
| Средняя урожайность ц/га | 32 | 40 | 45 | 48 | 49 | 51 |
| Абсолютный прирост базисный | - | 8,0 | 13,0 | 16,0 | 17,0 | 19,0 |
| Абсолютный прирост цепной (по годам) | - | 8,0 | 5,0 | 3,0 | 1,0 | 2,0 |
| Темп роста базисный | - | 125,00% | 140,63% | 150,00% | 153,13% | 159,38% |
| Темп роста цепной (по годам) | - | 125,00% | 112,50% | 106,67% | 102,08% | 104,08% |
| Темп прироста базисный | - | 25,00% | 40,63% | 50,00% | 53,13% | 59,38% |
| Темп прироста цепной (по годам) | - | 25,00% | 12,50% | 6,67% | 2,08% | 4,08% |
| Абсолютное содержание 1-го %-та прироста | - | 0,32 | 0,400 | 0,450 | 0,480 | 0,490 |
2)Рассчитаем
среднегодовые темпы роста ![]() урожайности пшеницы по формуле:
урожайности пшеницы по формуле:
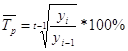 , где t –
количество лет
, где t –
количество лет
тогда, среднегодовой темп роста урожайности пшеницы с 1994 г. по 1999 г.:
![]()
среднегодовой темп роста урожайности пшеницы с 1995 г. по 1999 г.:
![]()
Рассчитаем среднегодовые
темпы прироста ![]() урожайности пшеницы по формуле:
урожайности пшеницы по формуле:
![]() ,
,
тогда, среднегодовой темп прироста урожайности пшеницы с 1994 г. по 1996 г.:
![]()
среднегодовой темп прироста урожайности пшеницы с 1995 г. по 1996 г.:
![]()
Изобразим исходные данные графически (см. рисунок 2)
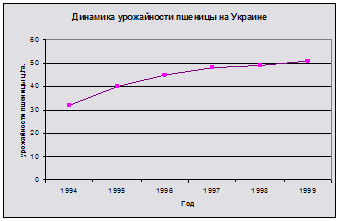
Рисунок 2 – Динамика урожайности зерна на Украине с 1994 по 1999 год
Вывод: график показывает, что на Украине с 1994 г. по 1999 г. наблюдалась тенденция увеличения урожайности пшеницы.
Задача 5.18
Имеются данные о затратах на производство продукции и изменении ее себестоимости по кожгалантерейной фабрике (см. таблица 9).
Таблица 9
| Наименование изделий | Общие затраты на производство продукции во 2-м кв., тыс. грн. | Изменение себестоимости изделия во 2-м кв. по сравнению с1-м кв., % |
| Сумки дамские | 74,6 | 10 |
| Портфели | 66,5 | 5 |
| Сумки хозяйственные | 75,5 | - |
Определите:
1) общий индекс себестоимости
2) общий индекс физического объема
3) общий индекс затрат при условии, что затраты на производство во 2-м квартале по сравнению с 1-м кварталом увеличились на 25%.
Решение
| Наименование изделий | Общие затраты на производство продукции во 2-м кв., тыс. грн. | Общие затраты на производство продукции в 1-м кв., тыс. грн. |
| Сумки дамские | 74,6 | 82,06 |
| Портфели | 66,5 | 69,825 |
| Сумки хозяйственные | 75,5 | 75,5 |
1) общий индекс себестоимости
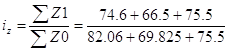 =0,953 (95,3%)
=0,953 (95,3%)
Вывод: общий индекс себестоимости показывает, что во 2-м периоде по сравнению с 1-м себестоимость за единицу продукции в среднем снизились на 4,7%.
2) Общий индекс
физического объема продукции ![]() определяется по формуле:
определяется по формуле:
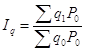 ,
,
тогда имеем:
![]() (104,97%)
(104,97%)
Вывод: общий индекс физического объема показал, что в 2-м периоде по сравнению с 1-м выработка продукции возросла на 4,97%.
3) Общий индекс затрат при условии, что затраты на производство во 2-м квартале по сравнению с 1-м кварталом увеличились на 25%.
Общий индекс затрат
![]() , где З2=74,6+66,5+75,5=216,6 при
условии увеличения на 25% получим З2=216,6+216,6*0,25= 270,75, а З1=82,06+69,825+75,5=227,385
, где З2=74,6+66,5+75,5=216,6 при
условии увеличения на 25% получим З2=216,6+216,6*0,25= 270,75, а З1=82,06+69,825+75,5=227,385
![]() (119,07 %)
(119,07 %)
Вывод: общий индекс затрат на продукции при условии увеличения на 25% показали, что во 2-м периоде по сравнению с 1-м затраты на продукции повысятся на 19,07 %.
Задача 6.21
Имеются данные о товарообороте магазина потребительской кооперации таблица 10
Таблица 10
| Товарная группа | Продано товаров в фактических ценах тыс.грн. |
|
|
| 2003 год | 2004 год | ||
| картофель | 63,00 | 71 |
|
| Фрукты и цитрусовые | 49,50 | 52,5 |
|
В 2004г по сравнению с 2003г. Цены на картофель повысились на 25%, а на цитрусовые и фрукты на 35%.
Определите:
1) Общий индекс товарооборота в фактических ценах.
2) Общий индекс цен и сумму дополнительных расходов населения в 2004г. При покупке картофеля и фруктов в данном магазине.
3) Общий индекс товарооборота физического объема, используя взаимосвязь индексов.
Решение
1) Общий индекс товарооборота в фактических ценах вычисляется по формуле:
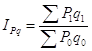 ,
,
![]() (109,7 %)
(109,7 %)
Вывод: индекс цен товарооборота в фактических ценах в отчетном периоде увеличилась по сравнению с базисным на 9,7%. Это увеличение обусловлено изменением средних цен на товарах в магазине.
2) Общий индекс цен и сумму дополнительных расходов населения в 2004г. При покупке картофеля и фруктов в данном магазине определяется по формуле:
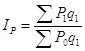
![]() ,
,![]() , тогда
, тогда
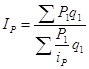 =
=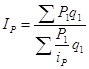 =
=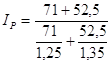 =1,291 (129,1%)
=1,291 (129,1%)
Сумма дополнительных расходов
I= ![]()
![]() 36,125 тыс.грн.
36,125 тыс.грн.
Вывод: общий индекс цен постоянного состава показывает, что средняя цена за 1 кг картофеля в отчетном периоде увеличилась по сравнению с базисным на 29,1%. При увеличении цен на товары сумма дополнительных расходов составила 36,125 тыс. грн.
3) Общий индекс товарооборота физического объема, используя взаимосвязь индексов
![]() ,
,
![]()
Вывод: общий индекс товарооборота физического объема составил 0,85%, т.е. товарооборот уменьшился на 15%
Задача 7.12
По данным задачи 1.12 для
выявления тесноты связи между возрастом рабочих (результативный признак Y) и оплатой труда (факторный признак X) вычислите коэффициент детерминации.
Решение. Коэффициент детерминации ![]() определяется по формуле:
определяется по формуле:
![]() ,
,
где ![]() - межгрупповая дисперсия,
- межгрупповая дисперсия,
![]() - общая дисперсия.
- общая дисперсия.
Межгрупповая дисперсия определяется по формуле:
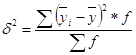 ,
,
где ![]() - среднее значение результативного
признака по каждой группе,
- среднее значение результативного
признака по каждой группе,
![]() - среднее по совокупности,
- среднее по совокупности,
f - частота результативного признака.
Общая дисперсия определяется по формуле:
![]()
Аналитическую таблицу берем из задачи 1.12 (см. таблицу 11)
Таблица 11
| № группы | Группа рабочих по стажу, лет | Число рабочих, чел. | Возраст, лет | Месячная зарплата, грн. | ||
| всего | Средний по группе | Всего | Средняя по группе | |||
| I | 18-25,2 | 5 | 117,0 | 23,4 | 1460,0 | 292,00 |
| II | 25,2-32,4 | 5 | 142,0 | 28,4 | 1660,0 | 332,00 |
| III | 32,4-39,6 | 4 | 144,0 | 36,0 | 1550,0 | 387,50 |
| IV | 39,6-46,8 | 4 | 173,0 | 43,3 | 1700,0 | 425,00 |
| V | 46,8-54 | 2 | 104,0 | 52,0 | 900,0 | 450,00 |
| Всего: | 20 | 576,0 | 36,6 | 7270,0 | 377,3 |
Рассчитаем межгрупповую дисперсию:
![]()
Для расчета общей
дисперсии необходимо найти ![]() для этого построим аналитическую таблицу (см. таблицу
12)
для этого построим аналитическую таблицу (см. таблицу
12)
Таблица 12
| Рабочий | Возраст, число лет, X | Месячная зарплата, грн., Y |
|
| 1 | 25 | 280 | 78400 |
| 2 | 24 | 310 | 96100 |
| 3 | 46 | 490 | 240100 |
| 4 | 45 | 420 | 176400 |
| 5 | 42 | 360 | 129600 |
| 6 | 50 | 410 | 168100 |
| 7 | 29 | 340 | 115600 |
| 8 | 36 | 390 | 152100 |
| 9 | 54 | 490 | 240100 |
| 10 | 29 | 350 | 122500 |
| 11 | 18 | 200 | 40000 |
| 12 | 37 | 380 | 144400 |
| 13 | 25 | 290 | 84100 |
| 14 | 30 | 320 | 102400 |
| 15 | 26 | 310 | 96100 |
| 16 | 36 | 400 | 160000 |
| 17 | 40 | 430 | 184900 |
| 18 | 28 | 340 | 115600 |
| 19 | 35 | 380 | 144400 |
| 20 | 25 | 380 | 144400 |
| Всего | 680 | 7270 | 2735300 |
Рассчитаем общую дисперсию:
![]()
Рассчитаем коэффициент детерминации:
![]() (59,7 %)
(59,7 %)
Вывод: коэффициент детерминации показывает, что возраст на среднемесячную заработную плату влияет на 59,7 %, остальные 40,3% - влияние других факторов.
Список использованной литературы:
1. Практикум по курсу "Статистика" для студентов всех специальностей. Часть 1 /Сост.:Акимова Е.В. , Маркевич О.В. – Краматорск, ДГМА, 2002 – 59 с.
2. Практикум по курсу "Статистика" для студентов всех специальностей. Часть 2 /Сост.:Акимова Е.В. , Маркевич О.В. – Краматорск, ДГМА, 2002 – 54 с.
3. Теория статистики:Учебник /Под ред. проф. Р.А.Шмойловой.- 3-е изд., перераб.- М.: Финансы и статистика, 2002.-560 с.:ил.
4. Практикум по теории статистики:Учеб. пособие /Под ред. Р.А.Шмойловой.- М.: Финансы и статистика, 2003.- 416 с.:ил.
| Статистика | |
|
Университет экономики и управления Горячих М.В. СТАТИСТИКА Учебно-методическое пособие для самостоятельного изучения дисциплины г. Симферополь 2003 ... Индекс сезонности - это процентное отношение одноимённых месячных (квартальных) фактических уровней рядов динамики к их среднегодовым или выровненным уровням. По данным таблицы вычислите цепные и базисные экономические показатели интервального ряда динамики: абсолютный прирост, темп роста, темп прироста. |
Раздел: Рефераты по экономике Тип: учебное пособие |
| Статистико-экономический анализ производства сахарной свеклы | |
|
Министерство сельского хозяйства Российской Федерации Воронежский государственный аграрный университет им. К.Д. Глинки Кафедра статистики и анализа ... Базисный абсолютный прирост - разность между каждым последующим и начальным уровнем ряда динамики, который принят за базу сравнения. Темп роста, рассчитанный базисным способом показывает, что рост урожайности сахарной свеклы также был максимальным в 2005 году и составил 201,68 %, а за период 1996-2000 был ... |
Раздел: Рефераты по экономико-математическому моделированию Тип: курсовая работа |
| Статистика цен и определение индексов | |
|
Содержание Введение Часть 1. Статистика цен 1.1 Задачи и система показателей статистики цен 1.2 Индекс потребительских цен (международный стандарт) 1 ... Важным вопросом теории и практики статистики цен является определение базисного периода, т.е. периода, по сравнению с которым индексы цен должны измерять динамику цен. При исчислении индексов цен на месячной основе возникает вопрос об отражении влияния фактора сезонности. |
Раздел: Рефераты по экономике Тип: курсовая работа |
| Статистические индексы и их применение в анализе динамики ... | |
|
... ВСЕРОССИЙСКИЙ ЗАОЧНЫЙ ФИНАНСОВО-ЭКОНОМИЧЕСКИЙ ИНСТИТУТ ФИЛИАЛ В Г.ТУЛЕ Курсовая работа по дисциплине "Статистика" на тему "Статистические индексы и их ... В зависимости от сроков исчисления (г) рассматриваются индексы базисные (с постоянной, неизменной во времени базой) и индексы цепные (если числовые значения индексируемой величины ... Индексы качественных показателей - индексы курса валюты, цен, себестоимости, производительности труда, заработной платы, урожайности и т.д. Индексируемые показатели этих индексов ... |
Раздел: Рефераты по экономике Тип: курсовая работа |
| Cтатистика конспект | |
|
Тема 1: Предмет и метод статистики Статистика как наука Метод статистики Методология статистики Основные категории статистики Основные задачи и ... Базисные темпы прироста: 8.5 Базисные и цепные индексы |
Раздел: Рефераты по статистике Тип: реферат |