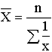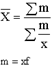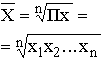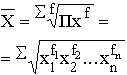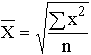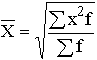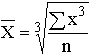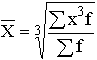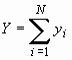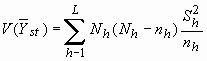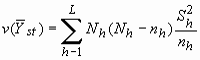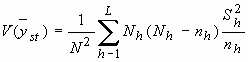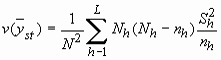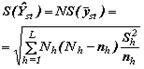Контрольная работа: Ряды динамики и распределения
Динамика выпуска продукции (млн. условных единиц) представлена в табл. 1.
Таблица 1
| Годы | Выпуск продукции, млн. усл. ед. |
| 926 | |
| 2 | 961 |
| 3 | 938 |
| 4 | 974 |
| 5 | 965 |
| 6 | 983 |
| 7 | 1015 |
| 8 | 1068 |
| 9 | 1122 |
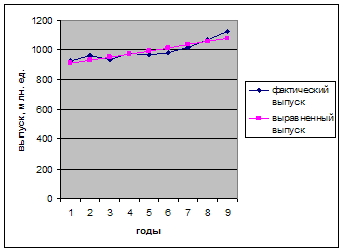
1. Построить ряд динамики. Изобразить ряд в виде линейного графика. Сделать вывод о наличии тенденции изменения уровня и о ее характере (увеличение уровня, снижение уровня, переломы тенденции, периоды одинакового типа тенденции).
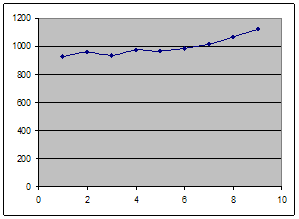
Из графика видно, что тенденция изменения уровня имеет характер увеличения выпуска продукции в зависимости от года. В третьем году наблюдался перелом кривой выпуска (снижение).
2. Рассчитать среднюю хронологическую (ряд динамики интервальный). При разном направлении изменения уровней выделить однородные по тенденции периоды и рассчитать частные хронологические.
3. Рассчитать систему производных показателей ряда динамики (абсолютные приросты, темпы роста и прироста, абсолютные значения одного процента прироста).
4. Показать взаимосвязь цепных и базисных темпов роста и прироста.
Средний уровень динамического ряда рассчитаем как среднюю хронологическую простую:
ycp=∑yi/n=8952/9 = 994,66
Рассчитать средний абсолютный прирост. При разном направлении изменения уровней выделить однородные по тенденции периоды и рассчитать частные средние абсолютные приросты.
Абсолютные приросты цепные и базисные:
∆цепной=yi – yi-1; ∆базисн=yi – y0
Темпы роста цепные и базисные:
Тцепной =100*yi / yi-1; Тбазисн=100*yi / y0
Темпы прироста цепные и базисные:
∆Тцепной =100*∆цепной / yi-1 = Тцепной – 100;
∆Тбазисн=100*∆базисн / y0= Тбазисн – 100
Абсолютное содержание 1% прироста:
А=∆цепной /∆Тцепной= yi-1/100
Средний абсолютный прирост:
∆yср=∑∆цепные/(n-1)=196/8 = 24,5
5. Рассчитать средний темп роста (три методики расчета). При разном направлении изменения уровней выделить однородные по тенденции периоды и рассчитать частные средние темпы роста.
Средний темп роста:
Трср=100 * (yконеч/ yнач)1/8=100 * (1122/926) 1/8= 1,21170,125 * 100 = 102,04
Средний темп прироста:
Т∆ср =Трср-100=102,04–100 = 2,04
6. Проанализировать тенденцию изменения уровня, самостоятельно избрав метод (скользящий средний уровень, аналитическое выравнивание по соответствующей модели). Выровненные значения показать на графике.
Y = a + bt
![]()
![]()
![]() где
n
– численность совокупности (в данном случае n =9).
где
n
– численность совокупности (в данном случае n =9).
![]() ,
,
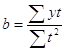 , в данном случае
, в данном случае
а = 8952/9 = 994,67 млн. ед.
b = 1223/60= 20,38 млн. ед.
Уравнение тренда: y = 994,67 + 20,38 t.
Выбираем модель изменения уровня – аналитическое выравнивание. Расчет приведен в таблице. Выровненные значения показаны на графике.
7. Проанализировать сезонные колебания объема выпуска продукции за три года. Рассчитать индекс сезонности. На графике изобразить сезонную волну.
Индексы сезонности показывают, во сколько раз фактический уровень ряда в момент или интервал времени t больше среднего уровня либо уровня, вычисляемого по уравнению тенденции f(t). При анализе сезонности уровни временного ряда показывают развитие явления по месяцам (кварталам) одного или нескольких лет. Для каждого месяца (квартала) получают обобщенный индекс сезонности как среднюю арифметическую из одноименных индексов каждого года. Индексы сезонности – это, по либо уровень существу, относительные величины координации, когда за базу сравнения принят либо средний уровень ряда, либо уровень тенденции.
Способы определения индексов сезонности зависят от наличия или отсутствия основной тенденции.
При наличии тренда индекс сезонности определяется на основе методов, исключающих влияние тенденции. Порядок расчета следующий:
· для каждого уровня определяют выровненные значения по тренду f(t);
·
рассчитывают отношения ![]() ;
;
при необходимости находят среднее из этих отношений для одноименных месяцев (кварталов) по формуле:
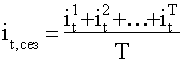 , (Т – число лет).
, (Т – число лет).
i1 = 926/912,48 =1,01
i2 = 961/932,86 = 1,03
i3 = 938 / 953,24 = 0,98
i4 = 974/973,62 = 1,00
i5 = 965/994 = 0,97
i6 = 983/1014,38 = 0,97
i7 = 1015/1034,76 = 0,98
i8 = 1068 / 1055,14 = 1,01
i9 = 1122 / 1075,52 = 1,04
График сезонной волны приведен на рисунке:
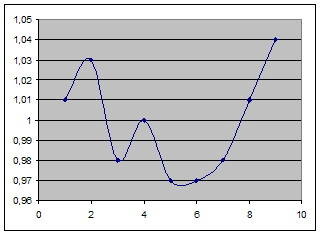
Расчет приведен в табл.
Задача 2
В табл. 2 представлено распределение покупателей по группам.
| Стоимость покупки, р | Количество покупателей |
| До 8 | 14 |
| 8–16 | 26 |
| 16–24 | 43 |
| 24–32 | 21 |
| 32 – 40 | 12 |
| 40–48 | 9 |
| 48 и более | 3 |
| Итого |
1. Построить ряд распределения. Изобразить ряд графически в виде гистограммы (полигона) и кумуляты распределения. Сделать вывод о характере распределения.
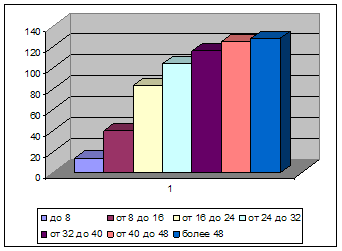
Рисунок – Кумулята распределения
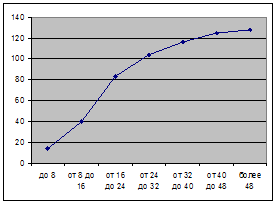
Рисунок – Кумулята распределения
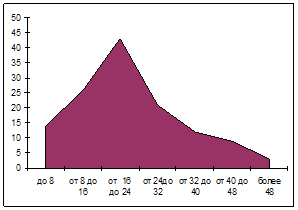
Рисунок – Полигон распределения
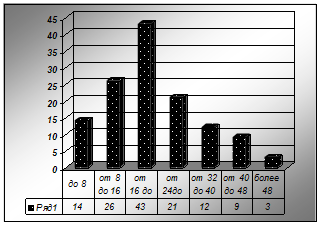
Рисунок – Полигон распределения
2. Рассчитать моду, медиану, первый и третий квартиль, средний уровень признака в совокупности; сравнить значение моды, медианы, средней и сделать вывод об асимметрии распределения. Рассчитать отклонение вариации: размах вариации, среднее линейное отклонение, дисперсию, среднее квадратичное отклонение, коэффициент вариации.
Первая квартиль (Q1) – значение признака у единицы, делящей ранжированный ряд в соотношении 1/4 и ¾, вторая квартиль равна медиане (Q2 = Ме), Третья квартиль (Q3) – значение признака у единицы, делящей ранжированный ряд в соотношении3/4 и 1/4. Порядковый номер Q1 определяется как ∑ f / 4, для Q3 – соответственно как 3/4∑ f
Таким образом, первый квартиль равен:
Q1 = 128/4 = 32
Q3 = ¾ *128 =96
Определяем показатель размаха вариации:
R = 48 – 8 = 40
Этот показатель улавливает только крайние отклонения и не отражает отклонений всех вариант в ряду.
xср= ∑хi* mi/ ∑mi=2800/128 = 21,875
Чтобы дать обобщающую характеристику распределению отклонений, исчисляют среднее линейное отклонение l, которое учитывает различие всех единиц изучаемой совокупности. Среднее линейное отклонение определяется как средняя арифметическая из отклонений индивидуальных значений от средней, без учета знака этих отклонений:
![]() .
.
l= 12,75/128 = 0,099
Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины.
![]() = 0,099/21,875=
0,455%
= 0,099/21,875=
0,455%
Дисперсия определяется следующим образом:
σ2=∑(xi – xcp)2* mi / ∑mi=17469,28/128=136,478
Среднее квадратичное отклонение равно:
σ= √σ2=√136,478=11,68
Коэффициент вариации:
V= 100%*σ/ xср=100*11,68/21,875 = 53,405%
Коэффициент осцилляции отражает относительную колеблемость
крайних значений признака вокруг средней ![]() = 40/21,875 *100 = 182,85%
= 40/21,875 *100 = 182,85%
Определим дисперсию другим методом:
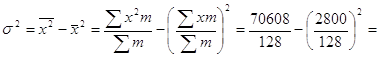 136,478
136,478
Дисперсия может быть определена методом условных моментов.
Момент распределения – это средняя m отклонений значений признака от
какой-либо величины А: если А = 0, то момент называется
начальным; если А = ![]() , то
моменты – центральными; если А = С, то моменты – условными.
, то
моменты – центральными; если А = С, то моменты – условными.
В зависимости от показателя степени К, в которую возведены отклонения (х – А)к, моменты называются моментами 1-го, 2-го и т.д. порядков.
Расчет дисперсии методом условных моментов состоит в следующем:
1. Выбор условного нуля С;
2.
Преобразование
фактических значений признака х в упрощенные х´ путем
отсчета от условного нуля С и уменьшения в d раз: 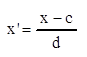
3.
Расчет 1-го условного
момента: 
4.
Расчет 2-го условного
момента: 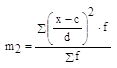
5.
Расчет 1-го порядка
начального момента: ![]()
6.
Дисперсии 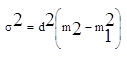
В качестве условного момента выбираем С=1, d = 2
|
Центральное значение интервала, хi |
|
|
( |
|
| 4 | 14 | 1,5 | 21 | 31,5 |
| 12 | 40 | 5,5 | 220 | 1210 |
| 20 | 83 | 9,5 | 788,5 | 7490,75 |
| 28 | 104 | 13,5 | 1404 | 18954 |
| 36 | 116 | 17,5 | 2030 | 35525 |
| 44 | 125 | 21,5 | 2687,5 | 57781,25 |
| 52 | 128 | 25,5 | 3264 | 83232 |
|
196 |
|
94,5 |
10415 |
204224,5 |
Расчет 1-го условного момента:

 = 10415/610 = 17,07
= 10415/610 = 17,07
Расчет 2-го условного момента:
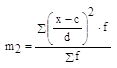
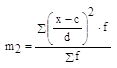 = 334,79
= 334,79
Расчет 1-го порядка начального момента: ![]() = 17,07*0,099+1 = 2,69
= 17,07*0,099+1 = 2,69
Расчет дисперсии:
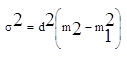 = 22 (334,79 – 17,072) = 136,48
= 22 (334,79 – 17,072) = 136,48
Модальный размер среднего размера покупки:
Мо=x0+h*(m2 – m1)/((m2 – m1)+(m2 – m3))
Модальный интервал (16–24), т. к. mmax=43
Мо =16+8*(43–26)/((43–26)+(43+21))=17,67
Медианный размер покупки:
Ме= x0+h*(1/2*∑mi-Sдо Ме)/mмед.инт
∑mi/2=128/2=64 – середина ряда.
Она попадает в медианный интервал (16–24).
Ме=16 +8*(1/2*128–40)/43= 20,46
Соотношение моды, медианы и средней арифметической указывает на
характер распределения признака в совокупности, позволяет оценить его
асимметрию. Если M0<Me<![]() имеет место правосторонняя
асимметрия. Если же
имеет место правосторонняя
асимметрия. Если же ![]() <Me<M0
– левосторонняя асимметрия ряда.
<Me<M0
– левосторонняя асимметрия ряда.
В данном случае M0<Me<![]() , т.е. 17,67 <20,46<
21,87, следовательно, имеет место правосторонняя асимметрия.
, т.е. 17,67 <20,46<
21,87, следовательно, имеет место правосторонняя асимметрия.
3. Указать другие методы расчета среднего уровня и дисперсии.
Виды степенных средних и методы их расчета приведены в табл.
|
Вид
степенной |
Показатель
|
Формула расчета | |
| Простая | Взвешенная | ||
| Гармоническая | -1 |
|
|
| Геометрическая | 0 |
|
|
| Арифметическая | 1 |
|
|
| Квадратическая | 2 |
|
|
| Кубическая | 3 |
|
|
Показать методику расчета дисперсии альтернативного признака.
Альтернативный признак принимает только 2 значения (1 и 0) с весами р и q соответственно.
Среднее значение альтернативного признака:
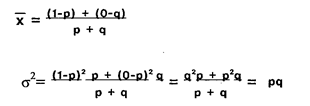
Назвать виды дисперсий в совокупности, разбитой на группы, сформулировать правило их сложения и методику расчета показателя тесноты связи между изучаемыми признаками.
Различают: общую дисперсию; межгрупповую дисперсию; внутригрупповую дисперсию; среднюю из внутригрупповых дисперсий.
Общая дисперсия (σ 2) измеряет вариацию признака во всей исследуемой совокупности, под влиянием всех факторов, обусловивших эту вариацию
Межгрупповая дисперсия (d 2) характеризует систематическую вариацию, то есть различия в величине изучаемого признака, возникающие под влиянием признака-фактора, который положен в основание группировки:
Внутригрупповая дисперсия (s I2) отражает случайную вариацию, то есть часть общей вариации, происходящей под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки:
Средняя из внутригрупповых дисперсий (s I2) рассчитывается по следующей формуле:
![]()
Существует закон, связывающий три вида дисперсий: общая дисперсия равна сумме из внутригрупповых и межгрупповых дисперсий, то есть:
s 2 = s I2+d 2
Логика этого закона проста: общая дисперсия, возникающая под воздействием всех факторов, должна быть равна сумме дисперсий, возникающих под влиянием всех прочих факторов, и дисперсии, возникающей за счет факторов группировки.
Три направления использования закона трех дисперсий:
o зная любые два вида дисперсий, всегда можно найти или проверить правильность расчета третьего вида;
o
![]() можно оценить удельное значение
фактора, лежащего в основе группировки, во всей совокупности факторов,
воздействующих на группировочный признак. Для этого исчисляется коэффициент
детерминации h 2 по формуле:
можно оценить удельное значение
фактора, лежащего в основе группировки, во всей совокупности факторов,
воздействующих на группировочный признак. Для этого исчисляется коэффициент
детерминации h 2 по формуле:
h 2 показывает долю общей вариации изучаемого признака, обусловленную вариацией группировочного признака;
o
![]() можно определить показатель тесноты
связи результативного и группировочного (факторного) признаков посредством
исчисления эмпирического корреляционного отношения: h Э:
можно определить показатель тесноты
связи результативного и группировочного (факторного) признаков посредством
исчисления эмпирического корреляционного отношения: h Э:
Оно имеет следующие пределы: 0 < h Э < 1
Если h Э = 0, то группировочный признак не влияет на результативный (связь между ними отсутствует). Если же h Э = 1, то результативный признак изменяется только в зависимости от группировочного признака (между ними существует функциональная связь).
Закон сложения трех видов дисперсий используется в дисперсионном анализе.
Задача 3
| Показатель | Товар-представитель | |||||||
| А | Б | В | Г | |||||
| Цена, р. | Физический объем, ед. | Цена, р. | Физический объем, ед. | Цена, р. | Физический объем, ед. | Цена, р. | Физический объем, ед. | |
| Базовый период | 8,4 | 1310 | 15,5 | 800 | 103 | 250 | 31,5 | 1845 |
| текущий | 10,5 | 1215 | 17,6 | 833 | 106 | 207 | 35,9 | 1810 |
| Товар-представитель | ||||||||
| А | Б | В | ||||||
| стоимость, тыс. руб. | индекс цен, % | стоимость, тыс. руб. |
индекс цен, % |
стоимость, тыс. руб. |
индекс цен, % |
|||
| база | отчет | база | отчет | база | отчет | |||
| 1685 | 1732 | 101,5 | 672 | 641 | 106,5 | 815 | 752 | 98,9 |
1. Рассчитать индивидуальные индексы цен и физического объема. Рассчитать общий индекс цен в агрегатной форме по методу Паше, Ласпейреса.
Модель расчета общих индексов методом агрегатного индекса
| Вид продукции | 2003 г | 2004 г | Стоимость продукции | |||||
| В текущих ценах | Текущего периода в сопоставимых ценах | Базового периода в текущих ценах | ||||||
| Цена, руб. | Физический объем, тыс. ед. | Цена, руб. | Физический объем, тыс. ед. | 2003 | 2004 | |||
| Символ |
p0 |
q0 |
p1 |
q1 |
p0q0 |
p1q1 |
p 0q1 |
p 1q0 |
| А | 8,4 | 1310 | 10,5 | 1215 | 11004 | 12757,5 | 13755 | 10206 |
| Б | 15,5 | 800 | 17,6 | 833 | 12400 | 14660,8 | 14080 | 12911,5 |
| В | 103 | 250 | 106,0 | 207 | 25750 | 21942 | 26500 | 57015 |
| Г | 31,5 | 1845 | 35,9 | 1810 | 58117,5 | 64979 | 66235,5 | 70875 |
| Итого | 158,4 | 2360 | 134,1 | 2250 | 107271,5 | 114339,3 | 120570,5 | 151007,5 |
2. Рассчитать общий индекс физического объема в агрегатной форме.
1.1. Агрегатный индекс физического объема
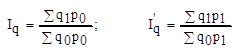
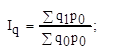 = 120570,5/107271,5 = 1.12
= 120570,5/107271,5 = 1.12
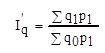 = 114339,3/151007,5 = 0.75
= 114339,3/151007,5 = 0.75
3. Рассчитать общий индекс стоимости. Показать взаимосвязь индексов цены, физического объема и стоимости.
Общий индекс 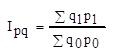 = 114339,3/107271,5 = 1.065
= 114339,3/107271,5 = 1.065
Система индексов имеет вид:
114339,3 2360 114339,3 120570,5 2250
107271,5 2360 120570,5 107271,5 2250
1,065 = 0,948*1,12
Если бы произошедшие изменения цен не сопровождались структурным перераспределением продаж, то средняя цена товара выросла бы в 0,948 раз, а только изменение структуры продаж вызвало бы рост средней цены на 12%. Одновременное воздействие двух факторов увеличило среднюю цену продаж на 6,5%.
| Вид продукции | 2003 г | 2004 г | ip | iq |
ip p0 |
iq*q0 |
||
| Цена, руб. | Физический объем, тыс. ед. | Цена, руб. | Физический объем, тыс. ед. | |||||
| Символ |
p0 |
q0 |
p1 |
q1 |
||||
| А | 8,4 | 1310 | 10,5 | 1215 | 1,25 | 0.93 | 9,45 | 1218.3 |
| Б | 15,5 | 800 | 17,6 | 833 | 1,135 | 1.041 | 17,59 | 832.8 |
| В | 103 | 250 | 106,0 | 207 | 1,03 | 0.828 | 106,09 | 207 |
| Г | 31,5 | 1845 | 35,9 | 1810 | 1,139 | 0.98 | 35,88 | 1808.1 |
| Итого | 158,4 | 2360 | 134,1 | 2250 | 4.55 | 3.78 | 169,01 | 4066.2 |
4. Рассчитать влияние факторов на изменение общей стоимости товаров.
Абсолютная сумма прироста оборота ![]() 114339,3 – 107271,5 = 7067,8 – оборот торговли
увеличился на 7067,8 тыс. руб.
114339,3 – 107271,5 = 7067,8 – оборот торговли
увеличился на 7067,8 тыс. руб.
Абсолютная сумма прироста оборота за счет изменения цен: ![]() 114339,3 – 120570,5 = -6231,2 – за счет изменения цен оборот торговли снизился на
6231,2 тыс. руб.
114339,3 – 120570,5 = -6231,2 – за счет изменения цен оборот торговли снизился на
6231,2 тыс. руб.
Абсолютная сумма прироста оборота за счет изменения количества
проданных товаров: ![]() 120570,5 – 107271,5 = 13299 – за счет изменения количества проданных товаров оборот
торговли увеличился на 13299 тыс. руб.
120570,5 – 107271,5 = 13299 – за счет изменения количества проданных товаров оборот
торговли увеличился на 13299 тыс. руб.
5. Показать методику преобразования общих индексов цен (Паше, Ласпейреса) и общего индекса физического объема в средние. Рассчитать общие индексы цен методом среднего индекса.
Индекс физического объема![]()
![]() = 158,4*4066.2 / 107271,5 = 6,00
= 158,4*4066.2 / 107271,5 = 6,00
Индекс цен Пааше
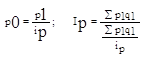
ip = 134,1/158,4 = 0.84
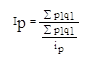 = 1/0,84 = 1,19
= 1/0,84 = 1,19
Индекс цен Ласпейреса: ![]()
![]() = 169,01
* 2360 / 107271,5 = 3,71
= 169,01
* 2360 / 107271,5 = 3,71
Модель расчета общего индекса как средней величины из индивидуальных
| Вид услуги | 2003 г | 2004 г | Изменение тарифов (+, -), % | Индивидуальный индекс | Условная выручка в постоянных ценах (пересчет выручки 2004 г. в цены 2003 г.) |
| А | 1685 | 1732 | +2,78 | 101,5 | 1780,49 |
| Б | 672 | 641 | -4,61 | 106,5 | 608,95 |
| В | 815 | 752 | -7,73 | 98,9 | 691,84 |
Расчет изменения тарифов:
А: (1732–1685) / 1732 * 100 = 2,78%
Б: (641–672) / 641 * 100 = -4,61%
С: (752–815) / 815* 100 = -7,73%
Индивидуальный индекс:
А: 1732/1685 = 1,028
Б: 641 / 672 = 0,95
С: 752/815= 0,92
Условная выручка в постоянных ценах (пересчет выручки 2004 г. в цены 2003 г.):
А: 1732*1,028 = 1780,49
Б: 641 * 0,95 = 608,95
С: 752 * 0,92 =691,84
Задача 4
Дать определение выборочного наблюдения и видов выборки. Назвать методы расчета предельной ошибки выборки для средней и для доли с вероятностью, и границы, в которые попадает генеральная или средняя доля.
Самостоятельно привести примеры расчета ошибок выборки.
Решение
Применение выборочного метода наблюдения включает следующие этапы:
· определение генеральной совокупности и единиц наблюдения, обладающих первичной информацией, необходимой для решения задач обследования;
· создание основы выборки;
· формирование выборочной совокупности путем отбора элементов основы;
· распространение собранных по выборке данных на генеральную совокупность.
Последний этап зависит от примененного способа отбора элементов в выборку и используемой формулы оценивания характеристик генеральной совокупности по данным выборки.
В статистической практике выборки извлекаются из конечных списочных основ. Однако единица основы, единица отбора и единица наблюдения могут отличаться. Например, это обычная ситуация при обследованиях населения и сельскохозяйственного сектора.
При рассмотрении любой схемы извлечения выборки должны быть учтены два фактора:
а) использовалась или нет вероятностная процедура;
б) наличие или отсутствие объективности в действиях специалиста, формирующего выборку.
Смысл объективности ясен и однозначен: любой специалист, производящий отбор, получил бы ту же самую выборку, т.е. выборку с теми же самыми свойствами. Субъективность означает, что специалисту, производящему отбор, позволено опираться на собственное суждение или интуицию относительно того, что является «хорошей» выборкой.
Рассматривая каждый из этих факторов на двух уровнях, можно выделить четыре типа выборок:
|
Роль,
которую |
Процедура отбора | |
| Вероятностная | Невероятностная | |
| Объективная | Выборки, сформированные вероятностным (случайным) образом | Выборки, сформированные на основе направленного отбора |
| Субъективная | Выборки, сформированные квазислучайным образом | Выборки, сформированные на основе суждения эксперта |
В статистической практике используются все четыре типа выборок. Однако обычно отдают предпочтение вероятностным (случайным) выборкам как наиболее объективным, поскольку имеется хорошо обоснованная теория, позволяющая понимать поведение таких выборок и оценивать их свойства (качество) отображения характеристик всей совокупности. Свойства и объективная ценность других выборок известны в меньшей мере.
Имеются два типа выборок, основывающихся на вероятностном способе отбора: выборки, отбираемые по объективным правилам вероятностного (случайного) отбора, и выборки, отбираемые, строго говоря, не по этим правилам (квазислучайные). Материалы сборника содержат значительное число примеров использования в статистической практике объективных вероятностных выборок. Одно из наиболее ценных качеств вероятностных выборок состоит в том, что можно оценить точность получаемых результатов по данным самой выборки.
Вероятностные выборки
В теории выборочных обследований рассматриваются выборки,
извлеченные из совокупностей (основ выборки), содержащих некоторое конечное
число единиц N. Эти единицы различимы между собой и число различных выборок
объема n, которые могут быть извлечены из списка N единиц, равно числу
сочетаний ![]() .
.
В выборочных статистических обследованиях в целях расчета параметров совокупности основное внимание направлено на изучение определенных свойств единиц, которые измеряются и фиксируются в процессе наблюдения для каждой единицы, включенной в выборку. Эти свойства называют признаками.
Хотя выборка используется для многих целей, обычно представляют интерес четыре характеристики совокупности:
среднее значение признака ![]() (например, среднее число занятых
на одном предприятии);
(например, среднее число занятых
на одном предприятии);
суммарное значение признака ![]() (например, выпуск продукции
предприятиями промышленности);
(например, выпуск продукции
предприятиями промышленности);
отношение двух суммарных или средних значений (например, отношение стоимости ликвидных активов к общей стоимости активов);
доля единиц в совокупности, относящихся к некоторой определенной группе (например, доля промышленных предприятий, оказывающих платные услуги населению) или обладающих определенным значением признака.
Главным вопросом методологии выборочного наблюдения является обеспечение приемлемого уровня ошибок получаемых значений характеристик совокупности, в том числе по требуемым разрезам, например, отраслям экономики, формам собственности и регионам России.
Полученные в результате выборочного наблюдения характеристики практически всегда несколько отличаются от характеристик генеральной совокупности. Эти отличия называются ошибками выборки (или репрезентативности), которые могут быть систематическими или случайными.
Систематические ошибки имеют место в том случае, когда нарушен принцип случайности отбора и в выборку попали единицы, обладающие какими-либо свойствами, не характерными для всех единиц генеральной совокупности. Случайные ошибки обусловлены тем обстоятельством, что даже при тщательной организации выборка не может в точности воспроизвести генеральную совокупность. В отличие от ошибок систематических, случайные ошибки являются вполне допустимыми, если они малы и могут быть оценены статистически.
Для измерения ошибки выборки, а также сравнения двух оценок, т.е. выявления более эффективной оценки, используют средний квадрат ошибки оценки (СКО), который измеряет ошибку относительно оцениваемого параметра совокупности:
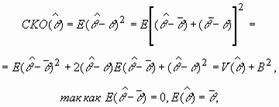
|
где E |
- | символ, заменяющий выражение «математическое ожидание величины»; |
|
|
оценка некоторой характеристики совокупности |
|
|
|
математическое ожидание |
|
|
|
- | смещение оценки; |
|
|
- | дисперсия оценки. |
Таким образом, СКО является критерием
достоверности оценки, который характеризует величину отклонений от истинного
значения характеристики совокупности ![]() .
.
В выборочных обследованиях способ
оценивания называется состоятельным, если оценка становится в точности равной
оцениваемому параметру для совокупности при n = N, т.е. когда
выборку составляет вся совокупность. Очевидно, что при простом случайном отборе
выборочное среднее ![]() и произведение
и произведение ![]() представляют собой
состоятельные оценки соответственно среднего и суммарного значений для
совокупности.
представляют собой
состоятельные оценки соответственно среднего и суммарного значений для
совокупности.
В данном контексте способ оценивания
называется несмещенным, если среднее значение оценки, взятое по всем
возможным выборкам данного объема n, в точности равно истинному
значению для совокупности, и это утверждение справедливо для любой конечной
совокупности значений ![]() и для любого n.
Например, при простом случайном отборе выборочное среднее
и для любого n.
Например, при простом случайном отборе выборочное среднее ![]() - несмещенная оценка
среднего значения признака,
- несмещенная оценка
среднего значения признака, ![]() - несмещенная оценка суммарного
значения Y для совокупности, где
- несмещенная оценка суммарного
значения Y для совокупности, где ![]() - среднее значение признака
- среднее значение признака ![]() по выборке.
по выборке.
В теории и практике выборочных обследований часто приходится рассматривать смещенные оценки. Это обусловлено следующими причинами. Во-первых, в некоторых случаях, особенно при оценивании отношений двух величин, смещенные оценки дают более достоверные результаты, чем несмещенные. Во-вторых, даже в случае использования теоретически несмещенных оценок ошибки наблюдения и неполучение ответов от респондентов могут привести к смещениям в распространенных результатах.
Кратко опишем некоторые, наиболее часто используемые в статистической практике способы формирования вероятностной выборки.
Простой случайный отбор. Простым случайным отбором называется способ, при котором извлечение единиц из совокупности для обследования осуществляется методом жеребьевки или с использованием таблиц или генератора случайных чисел без деления этой совокупности на какие-либо классы или группы.
Простую случайную выборку получают,
отбирая последовательно единицу за единицей. Единицы в совокупности нумеруются
числами от 1 до N, после чего выбирается
последовательность n случайных чисел, заключенных между 1
и N. Единицы совокупности, имеющие эти номера, составляют
выборку. На каждом этапе отбора такой процесс обеспечивает для всех еще не
выбранных номеров равную вероятность быть отобранными. Легко показать, что
равную вероятность быть отобранными имеют все ![]() возможных выборок.
возможных выборок.
Уже отобранные номера исключаются из списка, иначе одна и та же единица могла бы попасть в выборку более одного раза. Поэтому такой отбор называется отбором без возвращения. Отбор с возвращением легко осуществим, но им, за исключением особых случаев, пользуются редко, поскольку нет особых оснований допускать, чтобы одна и та же единица встречалась в выборке дважды.
При простом случайном отборе для получения выводов о параметрах совокупности используют выборочное среднее в качестве оценки среднего значения признака совокупности, а дисперсию признака по выборке – для оценки дисперсии признака совокупности. Для простой случайной выборки усредненные выборочные средние и дисперсии точно равны среднему и дисперсии признака совокупности.
Формулы оценивания при простом случайном отборе
| Статистические показатели | Истинное значение | Оценка |
| Суммарное значение признака |
|
|
| Среднее значение признака |
|
|
| Дисперсия признака |
|
|
| Дисперсия оценки суммарного значения признака |
|
|
| Дисперсия оценки среднего значения признака |
|
|
| Стандартная ошибка оценки суммарного значения признака |
|
|
| Стандартная ошибка оценки среднего значения признака |
|
|
| Коэффициент вариации оценки |
|
|
В таблице 2 использованы следующие обозначения:
|
i |
- | номер элемента; |
|
N |
- | объем (количество элементов) генеральной совокупности; |
|
yi |
- |
значение признака y i-го элемента, i = 1, 2,…, N или i = 1, 2,…, n; |
|
n |
- | объем (количество элементов) выборочной совокупности. |
Другие методы отбора часто оказываются предпочтительнее простого случайного отбора по соображениям удобства или повышения точности. Однако простая случайная выборка – наипростейший вид объективной вероятностной выборки, она служит основой для многих более сложных ее видов.
Расслоенный (типизированный) случайный отбор. Расслоенный случайный отбор – это отбор, предусматривающий предварительное разделение совокупности, содержащей N единиц, на слои и проведение простого случайного отбора в каждом слое.
Формулы оценивания при расслоенном отборе
| Статистические показатели | Истинное значение | Оценка |
| Суммарное значение признака |
|
|
| Среднее значение признака |
|
|
| Дисперсия оценки суммарного значения признака |
|
|
| Дисперсия оценки среднего значения признака |
|
|
| Стандартная ошибка оценки суммарного значения признака |
|
|
| Стандартная ошибка оценки среднего значения признака |
|
|
| Коэффициент вариации оценки |
|
|
| L | - | число слоев; |
| h | - | номер слоя; |
| Yh | - | суммарное значение признака y в h-м слое генеральной совокупности; |
| Nh | - | объем h-го слоя генеральной совокупности; |
|
|
- | среднее значение признака y в h-м слое выборки; |
| N | - | объем генеральной совокупности; |
|
|
- | среднее значение признака y в h-м слое генеральной совокупности; |
| nh | - | объем h-го слоя выборки; |
|
|
- |
истинное значение дисперсии для h-го слоя:
|
| i | - | номер элемента внутри слоя; |
| yhi | - | значение признака y i-го элемента слоя h; |
|
|
- |
несмещенная оценка дисперсии для h-го слоя:
|
Гнездовой (кластерный или серийный) отбор. Гнездовой отбор – способ формирования выборки, при котором единица отбора состоит из группы или гнезда более мелких единиц, называемых элементами. Таким образом, гнездовая выборочная единица – группа элементов, которая в процессе извлечения выборки рассматривается как одна единица. В простейшем случае элементы, составляющие гнездо, либо входят в выборку как группа, либо не входят в нее вообще.
Формулы оценивания при гнездовом отборе
| Статистические показатели | Истинное значение | Оценка |
| Суммарное значение признака |
|
|
| Среднее значение признака по гнездам |
|
|
| Среднее значение признака |
|
|
| Дисперсия оценки суммарного значения признака |
|
|
| Дисперсия оценки среднего значения признака |
|
|
| Стандартная ошибка оценки суммарного значения признака |
|
|
| Стандартная ошибка оценки среднего значения признака |
|
|
| Коэффициент вариации оценки |
|
|
|
i |
- | номер гнезда; |
|
M |
- | количество гнезд; |
|
Ti |
- |
суммарное значение признака в i-м гнезде; |
|
m |
- | количество выбранных гнезд; |
|
N |
- | объем генеральной совокупности; |
|
|
- | оценка объема генеральной совокупности. |
Систематический (механический) отбор. Для осуществления систематического отбора все единицы совокупности нумеруются в некотором порядке числами от 1 до N. Для получения выборки объемом n единиц сначала извлекается, например, случайным образом какая-либо единица из первых k = N/n единиц совокупности. После этого в выборку включается каждая k-я единица, начиная с уже извлеченной. Извлечение первой единицы определяет всю выборку. Такая выборка называется систематической выборкой каждой k-й единицы. Отношение N/n называется интервалом или шагом отбора.
Дисперсия среднего значения при систематическом отборе определяется по формуле:
![]() ,
,
| где |
N |
- | объем генеральной совокупности; |
|
S2 |
- | истинное значение дисперсии признака; | |
|
k |
- | шаг отбора; | |
|
n |
- | объем выборочной совокупности; | |
|
S2wsy |
- |
дисперсия единиц, принадлежащих одной и той же систематической выборке (wsy – от английского «within» – внутри и «systematic» – систематический): |
![]()
|
yij |
- |
значение признака j-го члена i-й систематической выборки, j =1, 2,…, n, i = 1, 2,…, k; |
|
|
|
- |
среднее значение признака i-й выборки. |
Многоступенчатый или многошаговый отбор (подвыборки). При организации статистических выборочных обследований широко применяется метод многоступенчатого отбора. Если исследуемая совокупность содержит некоторые группы и имеется информация о принадлежности элементов к той или иной группе, то в этом случае при выборочных обследованиях может быть удобным вначале осуществить случайную выборку из этих групп, а затем в целях экономии средств и времени не проводить обследование всех единиц отобранных групп, как при гнездовом отборе, а отобрать лишь часть элементов в каждой выбранной группе, т.е. осуществить двухступенчатый отбор. При многоступенчатом отборе извлечение единиц наблюдения осуществляется после нескольких последовательных случайных отборов групп.
Формулы оценивания при многоступенчатом (двухэтапном групповом отборе)
| Статистические показатели | Истинное значение | Истинное значение | |||
| Суммарное значение признака |
|
|
|||
| Количество элементов в генеральной совокупности |
|
|
|||
| Среднее значение признака |
|
|
|||
| Количество элементов в среднем на группу |
|
|
|||
| Дисперсия оценки суммарного значения признака |
|
|
|||
| Дисперсия оценки среднего значения признака |
|
|
|||
| Стандартная ошибка оценки суммарного значения признака |
|
|
|||
| Стандартная ошибка оценки среднего значения признака |
|
|
|||
| Коэффициент вариации оценки |
|
|
|||
|
N |
- | количество групп в генеральной совокупности; | |||
|
i |
- | номер группы; | |||
|
Yi |
- |
сумма признака i-й группы совокупности; |
|||
|
Mi |
- |
объем i-й группы, i=1,…, N; |
|||
|
j |
- | номер элемента в группе; | |||
|
yij |
- |
величина признака для j-го элемента в i-й группе совокупности; |
|||
|
n |
- | количество выбранных групп; | |||
|
mi |
- |
количество выбранных элементов в i-й выбранной группе, i =1,…., n; |
|||
|
|
|
- |
суммарное значение признака по выборке в i-й выбранной группе; |
||
|
|
- | среднее значение признака по совокупности; | |||
|
|
- |
среднее значение признака в i-й группе совокупности; |
|||
|
|
- |
несмещенная оценка для Y |
|||
|
|
- |
среднее значение признака в i-й выбранной группе; |
|||
|
|
- |
дисперсия совокупности между группами:
|
|||
|
|
- |
дисперсия внутри i-й выбранной группы:
|
|||
|
|
- |
несмещенная оценка дисперсии совокупности между группами:
|
|||
|
|
- |
несмещенная оценка дисперсии внутри i-й выбранной группы:
|
|||
В выборках квазислучайного типа предполагается наличие вероятностного отбора на том основании, что специалист, рассматривающий выборку, считает это допустимым (т.е. предполагается, обстоятельства таковы, что возможно рассматривать выборку как вероятностную). Обоснованность этого решения всецело зависит от обстоятельств, поэтому делать обобщения сложно.
Прямое использование суждения эксперта является наиболее общим методом намеренного включения единиц в выборку. Примером такого способа отбора является монографический метод, предполагающий получение информации только от одной единицы наблюдения, являющейся типичной по мнению организатора обследования – эксперта.
Выборки, сформированные на основе направленного отбора, извлекаются с помощью объективной процедуры, но без использования вероятностного механизма. Существует значительное число разнообразных способов направленного отбора.
Список литературы
1. Статистика: Курс лекций / Под ред. В.Г. Ионина. – изд. 2-е, перераб. и доп. – М.: ИНФРА-М, 2001. – 384 с.
2. Сборник задач по общей теории статистики: Учебн. пособие/ Под ред. Л.К. Серга. – М.: Филинъ, 1999. – 360 с.
3. Елисеева И.И., Юзбашев М.М. Общая теория статистики: Учебник. – М.: Финансы и статистика, 1998. – 368 с.
4. Курс социально-экономической статистики: Учебник / Под ред. М.Г. Назарова. – М.: ЮНИТИ, 2000.
5. Методологические положения по статистике / Госкомстат России. – М.: Логос, 1996. Вып. 1. – 674 с.
6. Статистический словарь /Под ред. Ю.А. Юркова. – М.: Финстатинформ, 1996. – 479 с.
7. Теория статистики: Учебник / Под ред. Р.А. Шмойловой. – М.: Финансы и статистика, 2000. – 576 с.
8. Экономическая статистика: Учебник / Под ред. Ю.Н. Иванова. – М.: ИНФРА-М, 1998. – 480 с.
9. Райзберг Б.А., Лозовский Л.Ш., Стародубцева Е.Б. Современный экономический словарь. - М., 2003
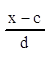 *f
*f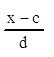 )2*f
)2*f