Учебное пособие: Фінансовий ринок та ризик

1 ФІНАНСОВИЙ РИНОК ТА РИЗИК. ОБЛІГАЦІЇ. ТЕПЕРІШНЯ ВАРТІСТЬ ОБЛІГАЦІЙ.

Для стислого описання теоретичних зведень по темі практичного заняття треба поділити теоретичний матеріал на кілька підтем:

-   нарощування простих відсотків;

-     нарощування складних відсотків;

-     потоки платежів, рента;

-     облігації;

При нарощуванні простих відсотків формула розрахунку майбутніх сум  по початковому внеску  по ставці  до кінця одиничного періоду має вид:

, (1.1)

тобто на , до кінця -го проміжку обчислення ця сума стане - кожна наступна сума більше попередньої на частку  від початкової суми .

Нарощена таким способом послідовність сум  є арифметична прогресія з початковим членом  і різницею .

Сума , нарощена по ставці  простих відсотків, через  проміжків нарахування стане .

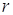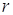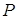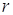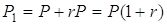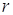 При нарощенні складних відсотків по ставці  кожна наступна сума зросте на частку  від попередньої. Таким чином, до кінця одиничного проміжку нарахування сума  зросте на частку  і стане , до кінця другого – ця сума зросте ще на частку  від 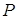, і стане 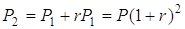. До кінця 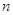-го проміжку - 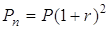. Таким чином, послідовність нарощених сум 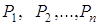 є геометрична прогресія з початковим членом 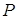 і знаменником прогресії 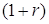. Сума 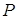, нарощувана по ставці  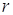складних відсотків через  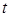проміжків нарахування стане

Перерахування майбутньої суми до дійсного моменту називається дисконтуванням чи розрахунком її сучасної величини.

Для простого нарощування відсотків коефіцієнт  - дисконтування дорівнює

,

а для формули складного –

.

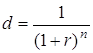Крім простого і складного нарощування відсотка на практиці використовують безупинні нарощування по ставці , тобто збільшення суми в  раз за одиничний проміжок часу, і в  раз за  проміжків нарахування.

Безперервним дисконтуванням називається операція, зворотна безперервному нарощенню, тобто зменшенню суми в  раз за  проміжків.

Потоки платежів, ренти

Потік платежів – це послідовність величин самих платежів і моментів часу, коли вони здійснені. Величиною потоку в момент Т називається сума платежів потоку, дисконтованих до цього моменту :

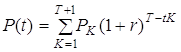 (1.2)

Якщо знайти величину потоку в момент Т, тоді в будь-який інший момент  величина потоку . Величина  називається сучасною (поточною) величиною потоку. Якщо є останній платіж, то величина потоку в момент цього платежу називається скінченою величиною потоку.

Потік платежів С с постійними проміжками між ними називається рентою.

Кінцева річна рента.

Це найпростіша рента: у неї тільки один платіж С в рік, тривалість її  років, річна процентна ставка . На рентні платежі нараховуються складні відсотки. Сучасна величина ренти  дорівнює:

, (1.3)

де З – розмір платежу.

«Вічна» річна рента. Під «вічною» річною рентою розуміється рента, послідовність платежів якої необмежена, передбачається, що рента буде виплачуватися необмежено довго. Нарощена величина цієї ренти нескінченна, але сучасна величина дорівнює

.

Облігації – це цінні папери, що характеризуються такими параметрами, як номінал ( - зазначений на лицьовій стороні облігації), проміжними платежами (купонами) і терміном погашення. Продаються і купуються облігації по поточній вартості . Під поточною вартістю облігації розуміють такий депозитний внесок , що при ставці відсотка  до моменту погашення дає номінал . Для  - периодной облігації - поточна вартість

.

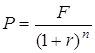Часто облігації мають купон, що характеризується купонною ставкою , що дає власнику купонний доход. Наприклад, якщо , а  у.о., то разовий купонний доход дорівнює 100 у.о. Поточна вартість ціна такої облігації складається з дисконтованих до сучасного моменту номіналу  і купонних виплат , тобто :

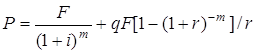 (1.4)

Приклади рішення типових задач

Задача 1.

У ході судового засідання з'ясувалося, що з вини пенсійного фонду гр.N протягом  років недоплачували  грн. пенсії щомісяця.

Суд поставив за обов'язок фонду виплачувати всі недоплачені гроші з відсотками ( річних). Яка сума виплати?

Рішення. Шукана сума є нарощена величина ренти з одиничним платежем 100 грн. та числом платежів 120. Ця сума дорівнює :

 (1.5)

По формулі складного нарахування відсотків ця сума  дорівнює

 грн.

Задача 2

Оцінити поточну прибутковість вкладень у безкупонну облігацію з номіналом  і курсовою вартістю , що здобувається на весь термін до строку погашення, який дорівнює  днів. Курс облігації вказується у відсотках до її номіналу. Для розрахунку поточної прибутковості до погашення по ставці простого відсотка слід скористатися формулою:

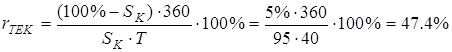 (1.6)

2 ВИДИ ЦІННИХ ПАПЕРІВ. АКЦІЇ

Ринок акцій надає зацікавленим особам можливості для вигідного чи вкладення залучення грошей. Акція – це ризикований цінний папір. Акція дає власнику акції певний дохід. Ризик акцій полягає в тому, що міняється їх курсова вартість під впливом ринкових механізмів, а також розмір дивідендів може коливатися. Так, для простих (звичайних) акцій він залежить від прибутку підприємства.

Зі збільшенням ризику, як відомо, вимоги інвестора до очікуваної прибутковості зростають.

Для розрахунку прибутковості цінного папера потрібно зіставити одержуваний по ній доход з ціною придбання. У випадку, коли в розрахунок приймається повний доход, отриманий інвестором як у вигляді дивидендів (), так і за рахунок різниці в цінах продажу  і покупки ( ), визначають повну прибутковість :

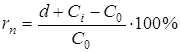 (2.1)

Показник поточної прибутковості , визначається з урахуванням поточного доходу , і поточного курсу , тобто :

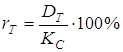 (2.2)

Акції характеризуються істотно більш високим, ніж облігації, ступенем невизначеності як по дивідендах, так і по зміні її ціни.

Курсові вартості виявляються на ринку цінних паперів у ході взаємодії попиту з пропозицією і являють собою ціни, по яких ці цінні папери продаються і купуються. Можна сказати, що формування курсових вартостей завжди відбувається під впливом цінових переваг його учасників.

Варто скасувати фундаментальну закономірність фондового ринку: вартість акцій зростає з ростом дивіденду ( ) і падає пропорційно розміру банківської ставки .

Формула для розрахунку курсу така:

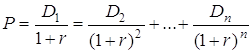, (2.3)

тобто курсова вартість оцінюється сумою всіх дисконтованих доходів. Так, ціна привілейованої чи простої акції з відомим розміром дивіденду визначається як поточна вартість «вічної» облігації, тобто . Ця формула отримана виходячи з того, що акція емітентом не погашається,

, а .

3 ДИВЕРСИФІКОВАНІСТЬ ПОРТФЕЛЮ ЦІННИХ ПАПЕРІВ. ОПТИМАЛЬНИЙ РИНКОВИЙ ПОРТФЕЛЬ. ЦІНА РИЗИКУ І b ЦІННОГО ПАПЕРУ

Під портфелем цінних паперів розуміють частковий розклад інвестицій , що входять у портфель. Створення портфеля цінних паперів забезпечує зниження ризику й дає можливість одержати портфель нульового ризику. Це можливо, якщо в портфель об'єднати різнорідні цінні папери (з коефіцієнтом кореляції ).

Однокритеріальна модель ефективності портфеля (модель Марковица).

Хай  частки ой цінного папера в портфелі,  - очікувана прибутковість ой цінного папера,  - коваріація доходностей тої і тої цінних паперів. Задача Марковица формулюється таким чином: знайти частки  розподілу вихідного капіталу, минимизуючі варіацію  ефективності портфеля:

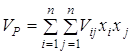,                               (3.1)

за умови, що забезпечується задане значення  очікуваної ефективності портфеля :

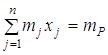,                                               (3.2)

і виконується бюджетний баланс:

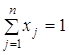.                                                      (3.3)

При комбінуванні в портфелі двох видів ризикових цінних паперів з характеристиками прибутковості  і ризику , тобто  й  і коефіцієнтом кореляції  модель Марковица має вид :

,                                  (3.4)

 .

Модель ефективного портфеля з без ризиковим компонентом (задача Тобина).

Ця задача відрізняється від моделі (3.1)-(3.3) тим, що інвестор крім ризикових цінних паперів враховує також можливість безризикових вкладень з ефективністю  в частках . Задача Тобина формулюється в такий спосіб: знайти частки , що минимизують  ризик портфеля :

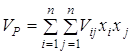,                              (3.5)

при обмеженнях:

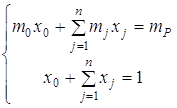                        (3.6)

З задачі Тобина випливає поняття  цінного папера. Величина  того цінного папера показує, яка частина ринкової прибутковості приходиться на прибутковість тої фірми:

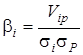 , (3.7)

де  - коваріація доходностей тої фірми і ринкового портфеля;

 - ризик того цінного папера і ринкового портфеля.

Тоді прибутковість того цінного папера, що входить у портфель, визначається по формулі :

                                 (3.8)

Якщо , то це значить, що прибутковість того цінного папера більше ринкової; при  - її прибутковість дорівнює ринкової; при  - прибутковість цінного папера менше ринкової, але більше, ніж безризиковий відсоток .

Ринкова ціна  ризику визначається у виді:

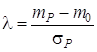 ,                                                (3.9)

де  - прибутковості портфеля цінних паперів і безризикова прибутковість;

 - ризик портфеля.

Задача.

Знайти оптимальний портфель  на траєкторії ефективних комбінацій із двох ризикових цінних паперів з характеристиками

, ; , , , .

Вказівки для рішення задачі

1. Записати рівняння ризику портфеля, скориставшись формулою (3.4).

2. Виключити , записати рівняння ефективної траєкторії.

3. Знайти абсцису крапки дотику на границі ефективності, записавши рівняння дотичної до функції в крапці дотику  :

 .

4. З огляду на те, що пряма проходить через крапку з координатами , , записати рівняння для невідомої прибутковості оптимального портфеля.

5. Вирішити рівняння й одержати структуру оптимального портфеля.

3          ОПЦІОННІ КОНТРАКТИ ТА ЇХ ВИДИ. ЦІНА ОПЦІОНУ.БІНОМІНАЛЬНА МОДЕЛЬ ВИЗНАЧЕННЯ ЦІНИ ОПЦІОНУ

Опціонні контракти – це термінові цінні папери, що представляють собою угода між двома сторонами про майбутнє постачання предмета контракту. Це умовна угода, при якій покупець контракту здобуває право чи виконати відмовитися від виконання контракту. За це право покупець опціону платить продавцю опціонну премію. Опціонна премія – це плата продавцю на той випадок, коли покупець відмовиться від виконання контракту. Існує опціон на покупку – це коллопціон і опціон на продаж – путо-опціон. Розрізняють європейський і американський типи опціонів колл і пута. У проблемі купівлі-продажу опціону центральним питанням є визначення його ціни.

Для розрахунку ціни опціону використовують біноміальну модель. Відповідно неї, увесь період дії опціонного контракту розбивається на рядок інтервалів часу, протягом кожного з яких курс акцій S може зростати з імовірністю Р або спадати з імовірністю (1 - Р). У кінці періоду акція відповідно стане Su i Sd, де u i d – це відсотки приросту і падіння курсової вартості акцій, . На малюнку 5.2 наведено дерево розподілу ціни акції для трьох часових періодів.

Рисунок 5.2 – Дерево розподілу ціни акції

Початкова ціна акції дорівнює S. За перший період  її курс може бути Su або Sd. За другий ,  або Sud і так далі.

До моменту закінчення контракту ціна С₀ опціону приймає два значення. Для опціону кол:

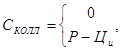 (4.1)

де  - ціна акції у момент виконання контракту;

 - ціна виконання контракту.

А для опціону пут опціонна ціна дорівнює:

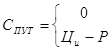 (4.2)

Для того, щоб розрахувати вартість опціону на початку періоду Т, необхідно визначити вартість опціону для початку кожного періоду , тобто в кожній крапці перехрещення гілок дерева. Дану задачу розв’язують послідовним дисконтуванням. Розрахунок ціни опціону починають з кінця дерева розподілу ціни.

Ціна опціону на початку періоду , тобто у крапках Su² i Sd² уявляє собою дисконтовану вартість ціни, що очікується, у кінці цього періоду і так далі для кожного попереднього відтінку часу. Ціна опціону  на початку періоду  визначається за формулою:

, (4.3)

де  - сума добутку значень ціни опціону, що очікується у кінці періоду , на їх імовірність.

Ціну опціону для кожної крапки на дереві розподілу зобразити другим рядком.

Для розрахунку відсотків росту, спаду акцій та їх імовірностей слід використовувати наступні формули:

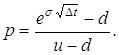    (4.4)

ПЕРЕЛІК ПОСИЛАНЬ

1. Капитоненко В. В. «Фінансова математика і її додатки». – М.: «Видавництво ПРІОР», 2009. – 144 с.

2. Малыхин В. И. «Фінансова математика». – М.: ЮНИТИ-ДАНА, 2000. – 247 с.

3. Шапкин А. С. «Економічні і фінансові ризики». – М.: Видавничо-торгова корпорація «Дашков і ДО⁰», 2008. – 544 с.

4. Буренин А. Н. «Ф'ючерсні, форвардні й опціонні ринки». – М.: Триола, 2008. – 240 с.