Дипломная работа: Формирование умственного приёма сравнения у младших школьников в процессе решения разноуровневых упражнений по математике
ЕВПАТОРИЙСКИЙ ПЕДАГОГИЧЕСКИЙ ФАКУЛЬТЕТ
КАФЕДРА ПЕДАГОГИКИ И МЕТОДИКИ НАЧАЛЬНОГО И ДОШКОЛЬНОГО ОБРАЗОВАНИЯ
КУРСОВАЯ РАБОТА
ФОРМИРОВАНИЕ УМСТВЕННОГО ПРИЁМА СРАВНЕНИЯ У МЛАДШИХ ШКОЛЬНИКОВ В ПРОЦЕССЕ РЕШЕНИЯ РАЗНОУРОВНЕВЫХ УПРАЖНЕНИЙ ПО МАТЕМАТИКЕ
Студентки 4 курса
Букановой Натальи Александровны
Евпаторийского педагогического факультета
(специальность: «Начальное обучение. Дошкольное
воспитание»)
Научный руководитель:
старший преподаватель
Глузман Неля Анатольевна.
Евпатория
2003
СОДЕРЖАНИЕ
ВВЕДЕНИЕ....................................................................................................... 3
РАЗДЕЛ 1.ПРОБЛЕМА РАЗВИТИЯ И ФОРМИРОВАНИЯ СРАВНЕНИЯ В ТЕОРИИ И ПРАКТИКЕ ОБУЧЕНИЯ
1.1. Роль сравнения в развивающем обучении................................................ 7
1.2. Содержание, структура и функции умственного приёма сравнения ......... 24
РАЗДЕЛ 2. ОПЫТНО-ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ПО ФОРМИРОВАНИЮ УМСТВЕННОГО ПРИЕМА СРАВНЕНИЯ У МЛАДШИХ ШКОЛЬНИКОВ В ПРОЦЕССЕ ИЗУЧЕНИЯ МАТЕМАТИКИ
2.1. Методика по развитию и формированию сравнения у младших школьников в процессе изучения математики......................................................................... 37
2.2. Дифференцированные упражнения по математике как средство формирования приёма сравнения.............................................................................................. 44
2.3. Планирование, организация и анализ результатов экспериментального исследования 48
ЗАКЛЮЧЕНИЕ И ВЫВОДЫ........................................................................... 53
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ........................................... 55
ПРИЛОЖЕНИЕ А............................................................................................. 60
ПРИЛОЖЕНИЕ Б.............................................................................................. 61
ПРИЛОЖЕНИЕ В............................................................................................. 62
ПРИЛОЖЕНИЕ Г.............................................................................................. 65
ВВЕДЕНИ Е
В новой концепции образования приоритетными целями являются развивающие. Рассматривая развивающие возможности математики, в большей степени говорят о развитии логического мышления. И это не случайно: математика имеет широкие возможности для умственного развития учеников благодаря своей системе исключительной ясности и точности понятий выводов и формулировок. Ошибочным с точки зрения современной психологии и дидактики является утверждение о том, что овладение самим содержанием курса математики автоматически формирует мышление школьников. Необходимо специально учить умению мыслить, давать учащимся знания о содержании и последовательности умственных действий, обеспечивающих усвоение курса математики. Однако конкретной программы логических приемов мышления, которые должны быть сформированы при изучении данного предмета, пока нет. В результате работа над развитием логического мышления школьников идет без знания системы необходимых приемов, без знания их содержания последовательности формирования. Это приводит к тому, что большинство учащихся не овладевают основными приемами мышления даже в старших классах школы, а эти приемы необходимы уже младшим школьникам: без них не происходит полноценного усвоения материала.
К числу фактов, определивших выбор темы нашего исследования, относится также недостаточная научная разработанность данной проблемы. Анализируя подходы и концепции, сложившиеся в теории и практике умственного развития, следует отметить исследования, посвященные формированию содержательных обобщений у детей (В.В. Давыдов, В.П. Иржавцева В.А. Крутецкий, В.Н. Осинская, В.Ф. Паламарчук, Л.Я. Федченко, С.А. Фокина, В.П. Хмель,), развитию компонентов мышления, методикам формирования приемов умственной деятельности у школьников (Л.В. Занкова, Н.Б. Истоминой, Е.Н. Кабанова-Меллер, Н.Н. Поспелова, В.И. Решетникова, З.И. Слепкань, Н.Ф. Талызиной, М.Н. Шардакова), формированию алгоритмов, способов формирования мышления учащихся средней школы (В.М. Косатая, Л.Н. Ланда, И.С. Якиманская), но развитие и формирование отдельных умственных приемов в условиях дифференцированного обучения младших школьников еще не нашла своего места в содержании математики начальных классов.
Анализ учебников и программ начальной школы показывает, что прием сравнения необходим учащимся уже в первом классе. Вместе с тем, пишет Талызина Н.Ф., если его не сделать предметом специального усвоения младшими школьниками, то он оказывается не усвоенным большинством учащихся до конца учебного года, что значительно отражается на дальнейшей успеваемости в средних классах.
Умение человека сравнивать, являясь одной из важнейших характеристик его ума, в то же время в большей степени способствует системности мышления. Поэтому чрезвычайно важна роль сравнения при формировании понятий, обобщений и систематизаций знаний. С другой стороны, использование сравнения в обучении открывает перед преподавателем возможность более доступно и наглядно излагать учебный материал.
Особенно важным является прием сравнения при изучении явлений, недоступных воображению, при усвоении знаний, которые выходят за пределы жизненного опыта человека. Прием сравнения позволяет углублять и уточнять изучаемый материал, помогает лучше сохранить его в памяти, вырабатывает умения систематизировать и классифицировать понятия, отношения и явления.
Изложенное выше обусловило выбор темы исследования: «Формирование и развитие умственного приема сравнения у учащихся начальных классов (на примере изучения курса математики)”.
Исследованием роли сравнения в учебном процессе и разработкой методики формирования этого приема занимались многие психологи, дидакты, методисты–математики (Г.И. Каганяк, Г.С. Костюк, В.Ф. Паламарчук, В.Н. Осинская, Н.Ф. Талызина, М.Н. Шардаков, П.М. Эрдниев и др.). В своих работах они выделяют сравнение как основу любой умственной деятельности. Так, Д.Н. Богоявленский, Н.А. Менчинская отмечают, что сравнение – обязательное условие всякой абстракции и всякого обобщения. Оно также необходимо при аналогии и классификации. К.Д. Ушинский неоднократно подчеркивал, что сравнение есть основа всякого понимания и всякого мышления.
Объектом исследования является процесс формирования умения сравнения у учащихся начальных классов.
Предмет исследования – организация учебной деятельности по формированию приема сравнения
Гипотеза исследования базируется на предположении о том, что при условии систематического и целенаправленного овладения приемами умственной деятельности будет не только способствовать оптимизации усвоения содержания предмета, но и повлияет на качественное изменение характера познавательной деятельности школьников.
Цель исследования заключается в обосновании и реализации методики формирования умственного приема сравнения у детей младшего школьного возраста в процессе изучения математики.
Цель работы и выдвинутая гипотеза позволили определить следующие основные задачи исследования:
– исследовать состояние проблемы в психолого-педагогической теории и практике школьного обучения, проанализировать психолого-педагогическую литературу по проблеме исследования;
– выявить содержание, структуру и функции умственного приема сравнения, установить его место и роль в процессе обучения математики;
– определить методические требования к проведению сравнения;
– обобщить опыт работы учителей, личный опыт сравнительной деятельности при обучении математике;
– проверить сформированность приема сравнения у учащихся в процессе опытно-экспериментальной работы.
Для решения поставленных задач были использованы такие методы научно-педагогических исследований:
– анализ отобранного программного материала, на котором можно реализовать проблему формирования умственного приема сравнения у младших школьников;
– анализ методов, средств, форм организации по формированию приема сравнения младших школьников;
– изучение психолого-педагогической, методической, философской литературы, анализ накопленного опыта работы учителей по проблеме формирования приема сравнения в начальной школе;
– изучение результатов деятельности младших школьников (проверка контрольных, самостоятельных работ и устного опроса) с целью определения уровня знаний и умений младших школьников при изучении отдельных тем.
Теоретическая и практическая значимость состоит в теоретическом обосновании идеи формирования приема умственной деятельности сравнения у учеников начальных классов. Разработана теоретическая модель системы работы над умственным приемом сравнения, включающая процессуальные и содержательные действия, которые обеспечивают высокий уровень осмысления хода решения математического задания, а также способствуют развитию элементов творческого мышления. Практическая значимость полученных результатов исследования состоит в апробации тестов и разработке комплекса тестовых заданий для определения сформированности умственного приема сравнения учеников в процессе изучения курса математики, в подготовке методических разработок, а также программ для статистической обработки результатов экспериментальной работы.
Курсовая работа состоит из введения, 2 разделов, заключения, выводов, списка использованной литературы, приложений (4). Общий объем работы – 54 страницы (до списка литературы).
Базой проведения экспериментального исследования была СОФМШ I – III ступени № 6 г. Евпатории, класс 1.
РАЗДЕЛ 1. ПРОБЛЕМА РАЗВИТИЯ И ФОРМИРОВАНИЯ ПРИЕМА СРАВНЕНИЯ В ТЕОРИИ И ПРАКТИКЕ ОБУЧЕНИ Я
Термин «развивающее обучение» активно используется в психологической, педагогической и методической литературе. Тем не менее, содержание этого понятия остается до сих пор весьма проблематичным, а ответы на вопрос: «какое обучение можно назвать развивающим?» довольно противоречивы. Это, с одной стороны, обусловлено многоаспектностью понятия «развивающее обучение», а с другой стороны, некоторой противоречивостью самого термина, т. к. вряд ли можно говорить о «неразвивающем обучении». Бесспорно то, что любое обучение развивает ребенка.
Однако нельзя не согласиться с тем, что в одном случае обучение как бы надстраивается над развитием, как образно отмечал Л. С. Выготский, «плетется в хвосте» у развития, оказывая на него стихийное влияние, в другом – целенаправленно обеспечивает его и активно использует для усвоения знаний, умений, навыков. В первом случае мы имеем приоритет информационной функции обучения, во втором – приоритет развивающей функции, что кардинально меняет построение процесса обучения.
Как отмечал Д.Б. Эльконин – ответ на вопрос, в каком соотношении находятся эти два процесса, осложнен тем, что сами категории обучения и развития разные. Эффективность обучения, как правило, изменяется количеством и качеством приобретенных знаний, а эффективность развития изменяется уровнем, которого достигают способности учащихся, т. е. тем, насколько развиты у учащихся основные формы их психической деятельности, позволяющей быстро, глубоко и правильно ориентироваться в явлениях окружающей действительности.
Давно замечено, что можно много знать, но при этом не проявлять никаких творческих способностей, т. е. не уметь самостоятельно разобраться в новом явлении, даже из относительно хорошо известной сферы науки [14, с. 64].
Приведем отрывок из монографии Н.Ф. Талызиной «Педагогическая психология» [41, с. 58] о выполнении учащимися второго класса следующего задания. Вначале были предъявлены два совершенно равных квадрата, а затем один из них был разрезан по диагонали на два треугольника, из которых, в свою очередь, был составлен один треугольник.

Приводим диалог с одним из учеников второго класса.
- Андрюша, ты хорошо учишься?
- Да.
- Молодец, скажи, вот эти фигуры как называются (показывают два квадрата)?
- Квадратики.
- Посмотри, они одинаковые или не одинаковые? Наложи один на другой и хорошо посмотри.
- Одинаковые.
- Одинаковые. Хорошо, значит, квадратики одинаковые, а теперь мы вот этот квадратик разделим на два треугольника (разрезаю) и из них построим один треугольник. А вот теперь скажи, одинаковые по величине эти фигуры: треугольник и квадрат?
- Они не одинаковые.
- А какая больше?
- Вот эта (показывает на треугольник).
- Ты уверен, что эта больше?
- Да.
Или другая аналогичная задача.
- Саша, скажи в бутылочках одинаковое количество жидкости или неодинаковое?
- Одинаковое.
- Посмотри внимательно, где тебе кажется меньше, где больше?
- Нигде.
- Значит, одинаково?
- Да.
- Хорошо. А теперь посмотри, что я сделаю: возьму вот эту бутылочку и переверну (экспериментатор ставит одну из бутылочек на горлышко). А теперь одинаковое количество жидкости в бутылочках или нет?
- Здесь больше. (Показывает на перевернутую бутылочку).
- Ты уверен в этом, Саша?
- Да.
- А если я опять поставлю бутылочку вот так (ставит бутылочку на донышко). А теперь как?
- Поровну.
- А если я теперь переверну первую бутылочку (первая бутылочка ставится на горлышко)?
- Здесь (показывает на первую бутылочку).
К сожалению, во втором классе такие ответы не такое редкое явление. Причина ошибки состоит в неумении ученика дифференцировать отдельные свойства предметов. В результате этого изменение одного свойства формы фигуры (в первом примере) и количества жидкости (во втором случае) он принимает за изменение другого (площади фигуры и уровня жидкости).
Аналогичные ошибки ученики делают и на материале русского языка. Например, на вопрос: «Слово изменяется по падежам, числам. Будет ли оно существительным?» – многие учащиеся отвечают утвердительно, что неверно, так как этими признаками обладает не только существительное, но и прилагательное.[41, с.59]
Причина всех этих ошибок – неумение применять логический прием сравнения. Поэтому, не случайно термин «развивающее обучение» методисты используют с большой осторожностью. Сложные динамические связи между процессами обучения и психического развития ребенка не являются предметом исследования методической науки, в которой реальные, практические результаты обучения принято описывать на языке знаний, умений, навыков.
Так как изучением психического развития ребенка занимается психология, то при построении развивающего обучения методика математики, несомненно, должна опираться на результаты исследований этой науки. А.Н. Леонтьев отмечает, что исследование формирования у детей понятий и логических (умственных) операций внесли важный вклад в науку: «Было показано, что понятия отнюдь не формируются в голове у ребенка по типу образования чувственных образования чувственных образов, а представляют собой результат процесса присвоения «готовых», исторически выработанных знаний и процесс этот происходит в деятельности ребенка. Обучаясь выполнению тех или иных действий, он овладевает соответствующими операциями». [22, с.142]
С.Л. Рубинштейн раскрывает механизм мыслительной деятельности следующим образом. Наличие проблемной ситуации, с которой начинается мыслительный процесс, всегда направленный на разрешение какой-либо задачи, свидетельствует о том, что исходная ситуация дана в представлении субъекта неадекватно, в случайном аспекте, в несущественных связях. Для того, чтобы в результате мыслительного процесса разрешить задачу, нужно прийти к более адекватному познанию. К такому все более адекватному познанию своего предмета и разрешению стоящей перед ним задачи мышление идет посредством многообразных операций, составляющих различные взаимосвязанные и друг в друга переходящие стороны мыслительного процесса. Таковыми являются сравнение, анализ и синтез, абстрагирование и обобщение. Все эти операции являются различными сторонами основной операции мышления – «опосредования», то есть раскрытия все более существенных объективных связей и отношений. Сравнение, сопоставляя вещи, явления, их свойства, вскрывает тождество и различие. Выявляя тождество одних и различия других вещей, сравнение приводит их к классификации. Сравнение является частью первичной формой познания: вещи познаются путем сравнения. Это вместе с тем и элементарная форма познания. [37,с. 324].
Как пишет В.В. Давыдов, «психическое развитие человека – это, прежде всего, становление его деятельности, сознания и, конечно, всех «обслуживающих» их психических процессов (познавательных процессов, эмоций и т.д.)» [ 7, с. 9 ]. Отсюда следует, что развитие учащихся во многом зависит от той деятельности, которую они выполняют в процессе обучения.
Из курса дидактики известно, что эта деятельность может быть репродуктивной и продуктивной. Они тесно связаны между собой, но в зависимости от того, какой вид деятельности преобладает, обучение оказывает различное влияние на детей. Репродуктивная деятельность характеризуется тем, что ученик получает готовую информацию, воспринимает ее, понимает, запоминает, затем воспроизводит[ 14, с. 65]. Это деятельность по образцу, по алгоритму. Учитель объясняет суть нового понятия, ученику нужно суметь объяснить ее самому. Прочитал в учебнике – нужно пересказать содержание, выделив в нем основное и главное. Учитель показал, как нужно действовать, – ученику нужно сделать так же, т.е. скопировать его действия. Получил задание – выполни его по алгоритму, т.е. предписанию, обобщенному правилу, заученному на уроке. Репродуктивное усвоение знаний – наиболее экономический путь формирования новых понятий и представлений. Основная цель такой деятельности – формирование у школьников знаний, умений, навыков, развитие внимания и памяти.
Продуктивная деятельность отличается от репродуктивной тем, что ученик самостоятельно применяет известные знания в новой ситуации или в известной ситуации находит новые для себя знания, новые правила действий. При этом не исключается и его действия по образцу. Махмутов М.И. отмечает, что в этом случае «деятельность ученика характеризуется рассуждением, размышлением, самостоятельным поиском способа умственного действия, т.е. логическим поиском в условиях проблемной ситуации, определенными этапами познавательного (мыслительного) процесса. Это ведет к воспитанию самостоятельности ума, формированию опыта деятельности, который невозможно получить по образцу, по алгоритму, поскольку на каждом этапе познавательного процесса требуется новое сочетание приемов умственной деятельности.[25, с. 27 – 28] Продуктивная деятельность связана с активной работой мышления и находит свое выражение в таких мыслительных операциях, как анализ, синтез, сравнение, классификация, аналогия, обобщение. Эти мыслительные операции в психолого-педагогической литературе принято называть логическими приемами мышления или приемами умственных действий.
Включение этих операций в процесс усвоения математического содержания – одно из важных условий построения развивающего обучения, так как продуктивная (творческая) деятельность оказывает положительное влияние на развитие всех психических функций. «… Организация развивающего обучения – справедливо отмечает И. С. Якиманская, – предполагает создание условий для овладения школьниками приемами умственной деятельности. Овладение ими не только обеспечивает новый уровень усвоения, но дает существенные сдвиги в умственном развитии ребенка. Овладев этими приемами, ученики становятся более самостоятельными в решении учебных задач, могут рационально строить свою деятельность по усвоению знаний» [14, с. 66]. Никто, несомненно, не будет с этим спорить. Каждый учитель должен развивать логическое мышление учащихся. Об этом говорится в объяснительных записках к учебным программам, об этом пишут в методической литературе для учителей. Однако конкретной программы логических приемов мышления, которые должны быть сформированы при изучении данного предмета, пока нет. В результате работа над развитием логического мышления школьников идет «вообще» – без знания системы необходимых приемов, без знания их содержания последовательности формирования. Это приводит к тому, что большинство учащихся не овладевают начальными приемами мышления даже в старших классах школы, а эти приемы необходимы уже младшим школьникам: без них не происходит полноценного усвоения материала.
Исследования Л.А. Аристовой, Ю.К. Бабанского, Л.В. Занкова, И.Я. Лернера, М.И. Махмутова, Н.А. Половниковой и др. показали, что среди факторов, активно влияющих на процесс обучения, ведущая роль принадлежит мышлению школьника, сформированным приёмам умственной деятельности. В условиях развивающего и воспитывающего обучения необходимо не только воспитывать потребность в знаниях, вооружать учащихся системой знаний, умений и навыков, но и современными способами познания. Центральным звеном развивающего обучения является формирование мышления учащихся как общей, интегративной способности личности, направленной на достижение целей обучения. В развивающем обучении диалектически взаимосвязаны все компоненты мыслительного процесса, и изменение одного из них приводит к изменению другого. [33, с. 12]
Под приемом умственной деятельности понимается логическая операция или совокупность логических операций, подчиненная разрешению задач определенного класса. В современной логике к логическим операциям относятся абстрагирование, сравнение, обобщение; к логическим действиям – доказательство, опровержение. Совокупность их дает новое цельное образование – прием умственной деятельности. [17, с. 131]
В психологии и дидактике различаются приёмы учебной работы и приёмы умственной деятельности. В приёмах учебной работы объединяются мыслительные и практические элементы действия: приёмы грамматического разбора, составление плана, «обратных» задач и т. д. Приёмы умственной деятельности относятся лишь к сфере мыслительной. Однако соотношение между этими приёмами подвижно: «Обычно в учебной деятельности ученика за пределами учебной работы спрятаны приёмы умственной деятельности». [16, с. 9] В 60–70 годы в психологии и педагогике (В.В. Давыдов, М.А. Данилов, Б.П. Есипов, И.Я. Лернер, Е.Н. Кабанова-Меллер, Н.А. Половникова, П.И. Пидкасистый и др.) проблема формирования умственной деятельности учащихся получила комплексное развитие. Психологами было дано системное определение понятий «деятельность», «действие», «операция». Критерий, по которому различаются действия и деятельность, определён А.Н. Леонтьевым.
По Леонтьеву, деятельность – это «всякий процесс взаимодействия субъекта с объектом, при условии, что направленность его в целом всегда совпадает с мотивом, в котором конкретизирована, определена потребность» [22, с. 102]. Деятельности без мотива не бывает. Действие же, по Леонтьеву, – это процесс, в котором цель и мотив не совпадают между собой. Действия, представляя собой относительно самостоятельные компоненты деятельности, характеризуются самостоятельной промежуточной целью, но их мотивы всегда совпадают с мотивами той деятельности, в которую эти действия входят. Действия по форме могут быть внешними (в том числе и практическими) и внутренними.
В содержание практической деятельности могут входить и умственные действия, а в состав теоретической деятельности и внешние действия. Действия учащегося, как компоненты его познавательной деятельности, могут выполняться тремя способами: вслед за действиями учителя, полностью самостоятельно или в процессе совместного творческого сотрудничества учителя и ученика.
Центральным с точки зрения организации и функционирования системы образования является понятие учебного процесса. Учебный процесс представляет собой совместную деятельность обучающего и обучаемого. Деятельность обучающего в учебном процессе называется обучением, а деятельность обучаемого – учением, или учебной деятельностью. Под учением понимают специально организованную деятельность людей, направленную на усвоение опыта предыдущих поколений.
Действия выполняются с помощью операций, представляющих собой способы реализации действий. Определённая последовательность операций характеризует «технический состав» действия. (М.И. Махмутов). Одно и тоже действие может быть выполнено с помощью различных операций, или различных способов. Главное свойство операций состоит в том, что они обладают относительной независимостью от сознания, в отличие от действия, которое предполагает и осознаваемую цель, и сознательный контроль его выполнения. Операции отвечают условиям, а не цели. Действия выполняются с помощью операций, представляющих собой способы реализации действий.
Понятие приём «умственной деятельности» широко используется в философской, психологической, педагогической и методической литературе в разных значениях. В философской литературе под приемом умственной деятельности понимается «логическая операция или совокупность логических операций, подчиненная разрешению задач определенного класса. В современной логике к логическим операциям относятся анализ, синтез, сравнение, абстрагирование, классификация, обобщение; к логическим действиям – доказательство, опровержение. Совокупность их дает новое цельное образование – прием умственной деятельности».[17, с. 130]
С различных точек зрения рассматривается приемы умственной деятельности в психологии. Так, С.Л. Рубинштейн разработал теорию научного обобщения, в основе которой лежит адекватное познание предмета изучения и разрешение стоящей перед учащимся задачи посредством многообразных операций. Таковыми, по мнению С.Л. Рубинштейна, являются анализ и синтез, сравнение, классификация, обобщение и абстракция, которые в реальном педагогическом процессе взаимосвязаны и переходят друг в друга.[37, с. 324 ]
Д.Н. Богоявленский, рассматривая формирование приемов умственной деятельности как один из путей развития мышления, определяет прием в качестве «совокупности, или вернее, системы умственных операций (действий), специально организованных для решения данного типа задач.
Создавая свою теорию всестороннего элементарного образования, И.Г. Песталоцци выделяет в нем первую часть – «Элементарное интеллектуальное образование, целью которого является правильное всестороннее и гармоническое развитие умственных задатков человека, обеспечивающих интеллектуальную самостоятельность, и привитие ему определенных развитых интеллектуальных навыков». В советской педагогике проблемами умственной деятельности занимались Л.С. Выгодский, Н.Ф. Талызина, Н.А. Менчинская Е.Н. Кабанова-Меллер и другие.
Л.С. Выгодский подчеркивал, что центральный вопрос умственной деятельности – это формирование осознанности и произвольности. Свое положение о том, что обучение должно идти впереди развития, он подкрепляет идеей, имеющей практическое значение, о «зоне ближайшего развития», на которую должен ориентироваться педагог.
Н.Ф. Талызина о сущности понятия приема умственной деятельности говорит: «В процессе решения задач, человек, как правило, использует не отдельные действия, а целые их системы. Обычно такую совокупность действий, приводящую к решению задач определенного класса, называют приемом, способом или методом решения.[43, с. 83]
Д.Б. Эльконин, исследуя значимость и роль содержания знаний в умственной деятельности учеников, создает обоснованную характеристику критериев отбора. В содержание обучения должны входить не только научные определения и факты, но и рассуждения доказательства, аргументы, позволяющие одновременно с овладением знаниями формировать способы познавательной деятельности по получению этих знаний. В обучении должны применяться проблемные беседы, дискуссии, отрабатываться различные приемы учебной работы и другие мыслительные операции.
Е.Н. Кабанова-Меллер различает понятия «прием учебной работы» и «прием умственной деятельности». К приемам учебной работы (решение задачи, исследование функций, составление графиков) она относит совокупность способов, которые могут быть объективно выражены в виде перечня действий, входящих в состав приема. Эти действия могут быть выражены в форме указаний выполнения задания, рекомендаций, правил. Приемы умственной работы (анализ, синтез, сравнение, классификация, обобщение, систематизация) – это способы, отражающие психологическую структуру познавательной деятельности и определяющие механизм решения конкретных учебных задач.[16,с. 56]
А.И. Раев, М.И. Махмутов, З.И. Слепкань, В.Н. Осинская указывают на то, что содержание приемов умственной деятельности объективно раскрывается в действиях, из которых они состоят. «Умственное действие – это психологический акт, представляющий собой содержательный структурный элемент умственной деятельности, имеющий определенную программу (в виде системы взаимосвязанных операций), направленную на идеальное, а в некоторых случаях материальное преобразование объекта из наличного состояния в намеченное, при котором совершается изменения и самого действующего субъекта). Действия описывается в виде алгоритма выполнения конкретного учебного задания. Осуществление действий приема дает общее направление познавательной деятельности, позволяя учащимся реализовать индивидуальный подход к решению учебной задачи, а педагогам – возможность гибко управлять процессом обучения. В зависимости от особенностей приема и степени усвоения учащимися его содержания состав действий может изменяться, количество варьироваться (увеличиваться или сокращаться).
Л.Б. Ительсон под приемами умственной деятельности понимает конкретные способы выполнения процедур анализа и синтеза, абстрагирования и обобщения, а пути овладения приемами умственной деятельности, по его мнению, могут быть различными в зависимости от характера самого приема и методики обучения. Автор представляет путь формирования приемов умственной деятельности схематически следующим образом: усвоение содержания приема → самостоятельное его применение → перенос на новые ситуации.
В психолого-педагогических исследованиях А.Е. Милеряна, И.Я. Лернера, В.Ф. Паламарчук одним из признаков приема умственной работы выделяется направленность системы действий на достижение конкретного результата деятельности. «Приемом работы, – пишет Лернер – можно назвать совокупность конкретных действий, составляющих способ достижения частной цели, входящей в систему деятельности по достижению общей цели… Совокупность приемов и составляет конкретную тактическую систему, ведущую к достижению стратегической цели обучения.
И.К. Журавлев, И.С. Якиманская отмечают процессуальный характер приемов умственной деятельности в ходе формирования знаний учащихся. Так, И.К. Журавлев указывает на то, что «учебный предмет представляет собой некую целостность, включающую два блока: основной – в нем представлено содержание, подлежащее усвоению, и блок, условно названный процессуальным, в нем содержатся для усвоения содержания, развития и воспитания школьников».[49, с. 138]
Основными признаками усвоения приемов умственной деятельности, по мнению Б.П. Есипова и Е.Н. Кабановой-Меллер, служит умение обучающихся осмыслить содержание действий приема и самостоятельно применить его в процессе решения новых разнообразных задач. Важным также является положение о том, что обобщение действий и приемов есть условием их широкого переноса.
В приемах учебной работы объединяются мыслительные и практические элементы действий, например, составление плана, решение «обратных задач. Приемы умственной деятельности относятся лишь к сфере мыслительной. Однако соотношение между этими приемами существует. На это указывает И.С. Якиманская, отмечая, что «приемы умственной деятельности представляет собой как бы интериоризацию приема учебной работы, заданного для усвоения в качестве норматива, образца» [49,с. 136].
Приемы умственной работы выступают как важное средство организации познавательной деятельности учащихся. Н.А. Менчинская обращает внимание на то, что в мыслительной деятельности происходит постоянная борьба между противоположными тенденциями – к сохранению, фиксированию приобретенного учебного опыта и к его модификации, изменению. «Уметь мыслить – это не только быть способным при требованиях определенной задачи воспроизвести (или актуализировать) имеющиеся, отвечающие данной задаче знания, но также быть способным к преодолению, отбрасыванию тех знаний (или систем), которые поставленной задаче не отвечают. Понимание учения как двойного процесса накопления знаний и овладения способами оперирования ими снимает противоречие» [16, с. 148].
Таким образом, обобщенный прием умственной деятельности – это система умственных действий обучающихся, направленная на организацию познавательной деятельности по самостоятельному усвоению системы знаний и решению задач определенного типа. Обобщенные приемы умственной деятельности являются основополагающими при проектировании учебного процесса учащихся, так как знания – являясь исходными в обучении – возникнув должны преобразовываться. Обучаемый, оперируя ими, формирует умения практически действовать и осваивает самостоятельно новые более рациональные способы решения специфических для учения задач. Функционирование системы обобщенных приемов умственной деятельности способствует активизации познавательной деятельности учеников, развитию у них системности, логичности, интегративности, вариативности в учебной работе школьников.
Существуют различные подходы к классификации приемов умственной деятельности.
Учитывая закономерности и особенности мыследеятельности школьников, принимая во внимание информацию, подлежащую изучению в школе, В.Ф. Паламарчук предлагает такую систему основных приемов мыслительной деятельности: 1) выделение главного; 2) сравнение; 3) обобщение и систематизация; 4) конкретизация; 5) определение и объяснение понятий; 6) доказательство и опровержение; 7) моделирование; 8) системный подход. Это – логико-дидактическая классификация основных способов умственной деятельности, которая применяется при решении любых задач. Эти приемы не являются равноценными с точки зрения решения разных задач: они могут быть целевыми, т.е. играть главную роль, и вспомогательными, обслуживающими основной прием. Например, одни задания требуют реализации как основного приема сравнения, другие в данном задании будут вспомогательными. В заданиях типа «докажите», «почему?» главным будут прием доказательства, остальные, в том числе выделение главного, сравнение, будут играть вспомогательную роль. Одни приемы могут включать в себя другие; например, прием обобщения включает в себя приемы выделения главного, группировки, систематизации и т.п. [33, 61–62]
Для методики и практики обучения математике особый интерес представляет характеристика умственных действий по усвоению математических понятий, предложенная З.И. Слепкань. Автор дает психологическую характеристику «общих умственных действий (операций)»: анализа, синтеза, сравнения, абстрагирования, конкретизации, обобщения, лежащих в основе любого вида познавательной деятельности школьника, а также специализации (математики): установление и использование аналогий, классификации и объединяющих их систематизации. К специфическим умственным действиям автор относит действие подведение под понятие и обратное ему действие выделение следствий. Однако, особую роль, подчеркивает З.И. Слепкань, при решении математических задач, формировании математических понятий, доказательству теорем отводится анализу и синтезу, как взаимосвязанным приемам умственной деятельности. [38, с. 36]
В своих исследованиях В.Н. Осинская обобщенные приемы умственной деятельности подразделяет на две группы – алгоритмического типа и эвристического типа. Первые – приемы мышления, соответствующие законам формальной логики. К ним относятся, например, алгоритмы решения типовых задач, конструирования, определения понятия через родо-видовые отличия. Такие приемы служат фундаментом знаний, на основе которых учащийся может выполнять новые задания, осваивать более сложные приемы умственной деятельности. Исследованиями психологов установлено: формирование приемов умственной деятельности алгоритмического типа – необходимое, но недостаточное условие развитие мышления. Оно необходимо потому, что, во-первых, содействует совершенствованию репродуктивного мышления, являющегося важным компонентом творческой деятельности, и, во-вторых, эти приемы служат тем фондом знаний, на основе которых ученик может решать новые для него задачи, осваивать более сложные приемы умственной деятельности. Вместе с тем, алгоритмы в обучении не исключают возможности творческого мышления, поскольку решение задач на основе предписании формируют у ученика установку на работу по готовому образцу. Формирование таких приемов должно сочетаться со специальным обучением приемам эвристического типа. Эвристические приемы стимулируют поиск вариантов решений новых учебных задач, развивают творческую деятельность и научно-образное мышление. К таким приемам относятся: выделение главного, существенного в учебном материале, обобщение, классификация, сравнение, конкретизация, абстрагирование, различные виды анализа, кодирования, аналогий. Использование приемов эвристического типа при решении новых учебных задач является главным показателем высокого уровня умственного развития учащихся [32, с. 12].
М.И. Махмутов отмечает, что в проблемном обучении необходимо развивать приемы умственной деятельности. Но проблемное обучение не сводится к тренировке учащихся в умственных действиях. Цель активизации в том, чтобы поднять уровень усвоения ими понятий и обучить не отдельным мыслительным операциям в случайном, стихийно складывающемся порядке, а в системе умственных действий для решения нестереотипных задач. Эта активность заключается в том, что ученик, анализируя, сравнивая, синтезируя, обобщая, конкретизируя фактический материал, сам получает из него новую информацию. Это расширение, углубление знаний при помощи ранее усвоенного и новое применение прежних знаний. Новому применению прежних знаний не может научить ни книга, ни учитель – это ищется и находится учеником, поставленным в соответствующую ситуацию. Постепенно овладевая системой творческих умений приводит к накоплению умений, навыков, опыта таких действий, изменению качества самой умственной деятельности. [25, с. 27 –28]
Один из способов создания проблемной ситуации – побуждение учащихся к сравнению, сопоставлению и противопоставлению фактов, явлений, правил, действий, в результате которых возникает проблемная ситуация. Например, урок математики в 3 классе на тему «Изменение частного». На доске вычерчены две таблицы:
a 6 12 48 96 a 90 45 30 15
b 2 2 2 2 b 3 3 3 3
a:b a:b
Учащиеся заполняют их и с помощью учителя устанавливают, что в данных примерах изменяется делимое, а делитель одинаков. Изменяется и частное. Педагог говорит: «Сопоставьте числа в таблицах и сделайте заключение об изменении частного». Возникает проблемная ситуация.[25, с. 100]
Сравнение связанно в учебном познании со всеми основными приемами умственной деятельности, особенно с выделением главного и обобщенного. Сравнение начинается с анализа и выделения главного; если учащиеся овладели умением выделять главное, прием сравнения формируется значительно быстрее и на более высоком уровне. Сформированный прием сравнения позволяет приступить к целенаправленному формированию умения обобщать; кроме того, любое сравнение должно заканчиваться обобщением, т. е. той добавкой к старым знаниям, ради которой совершается сравнение. Кто умеет сравнивать, тот легко овладеет приемами аналогии и доказательства. Применение приема сравнения способствует достижению положительных результатов в обучении и развитии, если оно вводится целенаправленно, осознанно, с учетом характера материала, сравниваемых объектов, возраста и уровня развития школьников.[33, с. 92 – 93]
Таким образом, сравнение является одним из приемов умственной деятельности. Сравнение, сопоставляя вещи, явления, их свойства, вскрывает тождество и различие. Выявляя тождество одних и различия других вещей, сравнение приводит их к классификации. Необходимо включение этой операции в процесс усвоения математического содержания, это одно из важных условий построения развивающего обучения.
1.2 Содержание, структура и функции умственного приёма
сравнения.
Особую роль в организации продуктивной деятельности младших школьников в процессе обучения математике играет прием сравнения. Как один из приемов умственной деятельности является наиболее применяемым в практике обучения математике.
Начинать работу по формированию приема сравнения нужно с выделения содержания этого приема, т. е. с выделения слагающих его действий.
Сравнение – это прием умственной деятельности учащихся, предполагающий установление сходства или различие между объектами изучения.
В логике сравнение – один из основных приёмов познания внешнего мира и духовных ценностей. Сравнение – важный способ перехода от созерцания к абстрактному мышлению. Познание любого предмета начинается с того, что мы отличаем его от других предметов и устанавливаем его сходство с родственными предметами. В этом проявляются две основные формы, в которых осуществляется сравнение: сопоставление и противопоставление.
Противопоставление – форма сравнения, направленная на уяснение отличительного в предметах и явлениях при выделении существенных признаков и свойств.
Однако только противопоставление, подчеркивающее особенность одного предмета в отличие от другого, по мнению Д.Н. Богоявленского и Н.А. Менчинской, не может обеспечить объединение в группу предметов, имеющих сходные черты. Поэтому при сравнении, проводимом с целью обобщения, противопоставление не может быть отделено от сопоставления.
Сопоставление – форма сравнения, направленная на выделение существенных свойств, общих для ряда объектов.
В мыслительной деятельности ученика противопоставление и сопоставление как формы сравнения выполняются в единстве и являются средством анализа и синтеза изучаемых понятий, фактов, предметов. Но в учебном процессе эти мыслительные операции чаще всего осуществляются последовательно.
По степени полноты различают частичные и полные сравнения.
Суть частичного сравнения в установлении только сходного или только отличительного. Если в объектах находят признаки сходства, то это – сопоставление, если ищут отличие – это противопоставление.
Полное сравнение требует установления сходства и отличия. Частичное сравнение эффективно на этапах восприятия и осмысления знаний, позволяет глубже осознать особенное в изучаемом материале, понять его связь с ранее усвоенными знаниями. Особенно важно различать свойства сходных понятий, чтобы предотвратить ошибки при их применении.
Познавательные задания на противопоставление могут быть такими:
1. Чем отличается объект А от объекта В?
2. Каких свойств нет в объекте А по сравнению с объектом В?
3. какими дополнительными свойствами обладает объект а по сравнению с объектом В?
4. Чем отличаются формулировки ? Чем отличаются задачи?
С целью обобщения материала школьникам предлагаются задания на сопоставление объектов (нахождение общего).[32, с. 18]
Полное сравнение эффективно на этапах обобщения и систематизации знаний (См. табл. 1.1).
Таблица 1.1
Уровни сравнения
| Уровни сравнения, их сущность | Действия, входящие в состав приема |
| Частичное сравнение – установление только общего, сходного свойства (сопоставление) или только общего, отличительного (противопоставление) в однородных объектах с определенной целью. |
- установление цели сравнения; - выделение основания для сравнения (одного из общих свойств); - отбор только общих (отличных, сходных) свойств в объектах по данному основанию; - вывод. |
| Полное сравнение – установление существенного общего (сопоставление) и несущественного отличительного (противопоставление) в однородных объектах с определенной целью. |
- определение цели сравнения; - выделение основания для сравнения; - отбор только общих существенных (отличных, сходных) свойств в объектах по данному основанию; - формулирование вывода. |
| Комплексное сравнение – сопоставление и противопоставление различных объектов или их элементарных частей по разнородным основаниям. |
- установить цель сравнения; - выделение оснований для сравнения; - сопоставление (противопоставление) объектов по выбранным основаниям; - формулировка вывода. |
По способам осуществления различают сравнения параллельные, последовательные и отсроченные. Параллельное сравнение – одновременное изучение взаимосвязанных понятий, теорем, задач, при изложении материала укрупненными блоками.
Последовательное сравнение – новый объект (понятие, отношение) сравнивается с раннее изученным.
Отсроченное сравнение – сравнение объектов (понятий, отношений), значительно удаленных по времени изучения.
С точки зрения операции сравнения все объекты делятся на сравнимые и несравнимые. Сравниваемыми называются объекты, имеющие какой – либо общий признак. Не сравниваемыми называются объекты, которые невозможно сравнить ни по объему, ни по содержанию. Следует подчеркнуть относительность этих определений: строго говоря, вообще не сравниваемых объектов нет, всегда можно найти какой-нибудь параметр или признак, по которому можно сравнить кажущиеся несравнимыми объекты. Понятно, что эти признаки или параметры в данном случае будут несущественными. И, если мы будем сравнивать объекты по каким-нибудь несущественным признакам, ничего позитивного от такого сравнения получить не удастся.
Всякий математический объект обладает определенными свойствами. Например, квадрат имеет четыре стороны, четыре прямых угла, равные диагонали. Можно указать и другие свойства квадрата.
Среди свойств объекта различают свойства существенные и несущественные для его выделения из других объектов. Свойство считают существенным для объекта, если оно присуще этому объекту и без него он не может существовать. Несущественные свойства – это такие свойства, отсутствие которых не влияет на существование объекта. Так, например, названые свойства квадрата являются существенными, а свойство «сторона АВ квадрата является вертикальной» несущественное. Если квадрат повернуть, то сторона АВ окажется расположенной по другому (Рис. 1.1).
В

 В С
В С
А С
А D D
Рис. 1.1.
Поэтому, чтобы понимать, что представляет собой данный математический объект достаточно знать его существенные свойства.
Как и любой приём умственной деятельности, сравнение имеет свой предмет, преследует определённую цель и предполагает свои пути реализации в процессе обучения. Дидактическую сущность приёма сравнения наиболее полно раскрыл в своих трудах В.Ф. Паламарчук.[33, с. 82]
При изучении математики предметом сравнения могут быть объекты окружающей действительности, понятия, признаки, результаты опытов, теоремы и их доказательства, структуры задач и методы их решения, операционный состав алгоритмов различных действий, способы учебной работы, а также факты, процессы, этапы работы. На уроках учащимся предлагают сравнить: выражения, структуры различных задач, алгоритмы сложения и умножения. При сравнении необходимо всегда соблюдать следующие логико-дидактические требования к объектам сравнения:
1. Сравнивать можно только однородные объекты, относящиеся к одному и тому же классу.
2. Общее в объектах сравнения можно устанавливать лишь в том случае, если их что-то отличает друг друга, а устанавливать разницу между ними можно только при наличии у них определённого сходства.
3. Несложные объекты, факты сравнивать легче, чем качества, признаки, процессы или категории. Поэтому объекты сравнения надо усложнять постепенно. Учить сравнению лучше начать с двух объектов, а затем постепенно увеличивать их число. При сравнении же сложных объектов необходимо вводить третий, более контрастный объект, активнее использовать сочетание словесных и наглядных методов.
Сравнивая, учащиеся должны четко понимать, с какой целью это делается. На уроке цели сравнения часто называет сам учитель; при этом необходимо стремиться вызвать интерес школьников к овладению данным приемом мышления.
Сравнение всегда целенаправленно, осуществляется под определённым углом зрения. Одни и те же объекты могут иметь сходство, если они рассматриваются с одних позиций, и могут отличаться, если сменить «точку отсчёта». В практике обучения учителя иногда ограничиваются выявлением лишь общих черт сравниваемых объектов, подчёркивая подобие одного другому, и редко стимулируют учащихся к параллельному поиску отличительных, противоположных признаков, черт и границ, что, снижает роль сравнения в процессе познавания и в развитии мышления школьников.
Цели сравнения в учебном процессе многообразны: обобщение и систематизация знаний, выделение в них главного, существенного, поиск общих признаков при формировании понятий; поиск аналогий в учебном материале; поиск закономерностей индуктивным путём; выдвижение гипотез; установление межпредметных связей в учебном материале и в способах его изучения; предотвращение ошибок по аналогии и выдвижение правдоподобных гипотез по аналогии; построение системы аналогов данного объекта; избежание подмены существенных свойств понятия несущественными свойствами; выделение существенного и несущественного в условии задачи, обобщение её структуры и осознание границ вариации её условия внутри данного типа задач. Сравнение является одним из рациональных приёмов заучивания и воспроизведения материала, но, сожалению, недостаточно применяется при изучении математики. Без сравнения невозможен перенос способа решения одной задачи на аналогичную. [32, с. 26-27]
Интерес к сравнению возникает у школьников по мере того, как они осознают его роль в успешном овладении знаниями, начинают понимать, что этот приём имеет общепознавательный характер, что, научившись сравнивать на уроках математики, они смогут использовать сравнение при изучении других школьных предметов, в жизненных ситуациях. В учебном процессе сравнение служит одним из средств объединения материала в крупные блоки. На уроке сравнение редко выступает как самоцель. Оно чаще всего является основой более сложных приёмов умственной деятельности или способом рационального заучивания материала.
Сравнение как приём применяется очень широко. Его можно использовать практически на всех этапах познания в процессе обучения: при восприятии нового материала, его осмыслении, уточнении и обогащении, систематизации и обобщении, применении в разных условиях. Правда, его место и функции будут не всегда одинаковы. Так, на этапе восприятия новых знаний сравнение, сформулированное в виде логического задания, помогает привлечь внимание учащихся главному, основному в рассказе учителя (или учебнике), тем самым способствуя формированию умения выделять главное. Задачи, поставленные на этапе подготовки к восприятию нового материала, активно помогают учащимся глубже осознать и более чётко представлять ведущие идеи, закономерности освящаемых явлений, тенденций, а стало быть, глубже постигать суть сообщаемой информации.
Сравнение как логический приём учебного познания особенно значительную роль играет на этапе осмысления информации, когда после восприятия учащимися нового материала, а также в процессе наблюдения или практических действий учитель даёт задачу (задание) на сравнение познанного на данном уроке с уже известным материалом. Сравнивание на этапе понимания, осмысления знаний помогает установлению связей теории с практикой.
На основе сравнения зачастую осуществляются обобщение и систематизация, без которых невозможен процесс обучения.
Дидактический приём сравнения (в тесной связи с другими) эффективен и при формировании таких качеств, как действенность, творческая направленность в применении знаний, для чего особенно целесообразны проблемные задания сравнительно-обобщающего типа.
По степени полноты различается полное и частичное сравнение. Первое требует установления как сходства, так и различия, а второе – только сходства или признаки сходства в объектах, мы имеем дело с их сопоставлением; если же устанавливаются только отличия, это будет противопоставлением.
Использование определённого вида сравнения зависит от цели урока, особенности материала, уровня сформированности у учащихся данного приёма. На этапах восприятия и осмысления материала целесообразно частичное сравнение, при общении и систематизации – полное.
Но какой должна быть последовательность сравнения, т.е. что нужно устанавливать сначала: сходство или различие между сравниваемыми объектами? Ответ на этот вопрос мы находим в психологии сравнения. При сравнении, как указывал ещё И. М. Сеченов, человек сначала сопоставляет объекты, как бы накладывает их один на другой «подобно тому, как в геометрии ученик накладывает фигуры треугольников, чтобы доказать их равенство». (Сеченов И.М. Кому и как разрабатывать психологию. – Избр. философ. и психолог. произв. М., 1947, с. 271.)
С целью дифференциации объектов учитель ставит вопросы или задачи на установление отличия. С целью обобщения материала предлагаются задания на сопоставление объектов (нахождение общего).
Сравнения различаются не только по степени полноты, но и по способам их осуществления. Они могут быть параллельными, последовательными и отсроченными. Параллельными будут сравнения синхронно изучаемого материала. Последовательным является сравнение фактов, явлений , качеств, процессов , которые изучаются хронологически, одно за другим. Отсроченным является сравнение объектов, которые изучались на разных уроках, значительно удалённых друг от друга по времени. Наиболее распространённым является последовательное сравнение. Отсроченное сравнение чаще используется при тематическом и итоговом повторении материала.
Процесс формирования у учащихся умений пользоваться приёмом сравнения, как и другие подобные процессы, имеет свою определённую этапность. Так, после первого этапа – накопления опыта сравнения – необходимо выяснить уровень сформированности умения пользования этим приёмом, для чего учитель, проводя контрольную работу, должен включать в неё и вопрос на сравнение. Причем никаких указаний, плана, правил учитель не должен давать. Анализ работ учащихся следует проводить по системе показателей, характерных для данного приёма: указана ли цель сравнения, сколько признаков отличия и сходства установлено, сделан ли вывод из сравнения. При анализе важно учитывать и характер признаков: тождественные, общие, конкретно-обобщенные, балластные. Определение полноты сравнения и характера установленных признаков дает возможность распределить работы по таким уровням:
1) работы тех учащихся, которые умеют лишь рядоположенно описывать объекты, не сопоставляя их;
2) работы тех, у кого есть описание по системе признаков (сначала изложены мысли об одном объекте в целом, потом о другом и т. д.);
3) работы с неполными сравнениями, когда ученики указывают либо сходство, либо отличие, но не по всем необходимым признакам, которые у них носят зачастую внешний, несущественный характер;
4) работы с полными сравнениями, когда учащиеся проводят их по системе существенных признаков отличия и сходства с указанием цели и вывода;
5) работы, в которых учащиеся переносят умение сравнивать с данного учебного предмета на другие, когда сравнение становится обобщенным приемом умственной деятельности. Данный уровень является высшим.
Умение сравнивать зависит от ряда факторов, в частности от уровня развития учащихся, сложности сравниваемых объектов, характера дидактического задания. Между умением сознавать сходство и отличие существуют довольно тесная связь. Но при стихийном формировании методов и приёмов работы даже старшеклассники не умеют сознательно сравнивать по признакам сходства и отличия, сто указывает на недостаточную гибкость, разносторонность их мышления.
Выяснив уровень сформированности умения сравнивать, необходимо приступать к следующему этапу – этапу мотивации, созданию атмосферы заинтересованности учащихся в овладении рациональными приёмами умственного труда. Учитель подробно анализирует каждую работу по основным структурным компонентам сравнения, а на следующем уроке производит детальный разбор достоинств и недостатков.
Четвертый этап формирования умений применять прием сравнения – осмысление сути приема и правил его реализации. Суть приема разъясняется учащимися в виде краткого определения. Затем в процессе беседы или инструктажа вводится правило-ориентир пользования данным приемом. Оно примерно таково:
1. Установи цель сравнения.
2. Проверь, знаешь ли ты материал про объекты, которые будешь сравнивать.
3. Выдели главные признаки, по которым будешь сравнивать.
4. Найди отличие и (или) сходство.
5. Сделай вывод из сравнения.
При изучении различных учебных предметов это правило может детализироваться. На этом этапе большое внимание уделяется последовательности действий при сравнении.
Пятый этап формирования – применение приема сравнения в классной и домашней работе, в устных ответах и письменных работах, во взаимоотношениях, при решении познавательных задач и выполнение заданий на сравнение.
Познавательная самостоятельность учащихся усиливается при постановке логического задания перед изложением, которое требует сравнения. Такой вид работы развивает самостоятельность ума школьников, формирует умение выделять главное, перераспределять внимание. Такая работа облегчается предложенным учителем планом сравнения, который помогает ученикам в работе по учебнику и в эвристической беседе, позволяющей более успешно формировать умение применять данный прием в самом процессе изучения нового материала, корректировать сравнения учащихся.
Эвристическая беседа открывает широкие возможности и для формирования мышления и мировоззрения. Сравнивая под руководством учителя явления, процессы, ученики глубже понимают их суть, учатся обобщать. Такая форма работы приучает школьников мыслить последовательно, логично, учит рассуждать, отстаивать свои взгляды. Сама же техника составления плана должна формироваться постепенно, начиная с I класса, общими усилиями всех преподавателей.
Не менее важным дидактическим приемом в формировании умения сравнивать является составление сравнительных таблиц, схем, графиков. Полезным дидактическим приемом является коллективное и самостоятельное составление подобных схем, помогающих конкретизировать сравнение, объединяющих чувственные и рациональные компоненты учебного познания.
Следующий по степени сложности познавательной деятельности является самостоятельная работа учащихся. Она облегчается знанием сути и правил и правил сравнения, готовым планом сравнения.
Умение самостоятельно решать познавательные задачи свидетельствует о том, что знания учащихся стали руководством к действию, сто они усвоены на творческом, действенном уровне. Это умение складывается постепенно, поэтапно: от образца, который дает учитель, через коллективное решение задач к самостоятельному, индивидуальному решению. Если же ученики не освоили исходных операций (анализ, выделение существенных признаков, классификация), то проводится несколько пропепедевтических упражнений.
Познавательные задания и задачи на сравнение успешно решаются, когда они соответствуют характеру учебного материала, охватывают главное в нём, а не отвлекают на частности. Задача или задание, сформулированные нестандартно, проблемно, вызывают интерес, будят внимание и включают механизм творческого мышления. Многие исследователи справедливо подчёркивают, что введение в систему работы школы познавательных заданий и задач позволяют формировать у детей творческие способности в активной деятельности, т. е. формировать опыт творчества, который иным путём приобрести невозможно. Любая задача или задание для своего решения требует применения определённого приёма умственной деятельности или совокупности этих приёмов, развивающих эти способности школьников.
К типичным дидактическим ситуациям, диктующим постановку заданий и задач на сравнение, можно отнести следующие:
§ Сравнение с целью выявления общего в явлениях, процессах.
§ Сравнение с целью выявления особенного, отличительного.
§ Полное сравнение: установление как сходства, так и отличия.
§ Сравнение с целью выявления главного, основного в явлениях, событиях, процессах.
§ Сравнение, имеющее целью выяснить отношение учащихся к объектам, дать оценку.
§ Сравнение, в процессе которого учащиеся устанавливают причинно-следственные связи между явлениями.
§ Сравнение с целью прогнозирования.
§ Сравнение, в процессе которого учащиеся конкретизируют общие представления и знания об объекте.
Перечисленные задачи на сравнение показывают единство и взаимодействие в учебной познавательной деятельности всех основных приёмов работы: выделение главного тесно связанно со сравнением и обобщением, сравнение и обобщение – с доказательством и конкретизацией.
Познавательные задачи на сравнение могут быть так называемых открытых и закрытых проблем.
Открытая проблема характеризуется тем, что ученик не может решить её, лишь мобилизовав свой прежний опыт: ему необходимы какие-то знания (новые способы действия). Создается проблемная ситуация для поиска новых знаний.
«Закрытая» проблема характеризуется там, сто для своего решения она требует применения полученных знаний, умений и навыков.
Выбор типа проблемы зависит от дидактической цели урока. Усвоение нового материала строится на открытых проблемах, применение полученных знаний опирается в большинстве своем на закрытии. Формулировка задания (задачи) на сравнение определяет и степень самостоятельного поиска, и степень его сложности. Краткая формулировка «Сравните…» усложняет задание, расчлененная – «Сравните… Укажите сходство… В чем отличие? Какова прогрессивность каждого из явлений?» – облегчает познавательный поиск.
Заключительным этапом формирования умений применять прием сравнения является перенос этих умений с одного предмета на другой и на внеучебную деятельность. Если учащиеся, научились пользоваться приемом сравнения на уроках, например, математики, без особого труда применяют на уроках русского языка чтении и в других условиях, значит, поставленная учителем цель достигнута.[33, с. 81 – 92]
Таким образом, сравнение связанно в учебном познании со всеми основными приемами умственной деятельности, особенно с выделением главного и обобщенного. Сравнение начинается с анализа и выделения главного; если учащиеся овладели умением выделять главное, прием сравнения формируется значительно быстрее и на более высоком уровне. Сформированный прием сравнения позволяет приступить к целенаправленному формированию умения обобщать; кроме того, любое сравнение должно заканчиваться обобщением, т. е. той добавкой к старым знаниям, ради которой совершается сравнение. Кто умеет сравнивать, тот легко овладеет приемами аналогии и доказательства. Применение приема сравнения способствует достижению положительных результатов в обучении и развитии, если оно вводится целенаправленно, осознанно, с учетом характера материала, сравниваемых объектов, возраста и уровня развития школьников.
РАЗДЕЛ 2. ОПЫТНО-ЭКСПЕРИМЕНТАЛЬНОЕ ИССЛЕДОВАНИЕ ПО ФОРМИРОВАНИЮ УМСТВЕННОГО ПРИЕМА СРАВНЕНИЯ У МЛАДШИХ ШКОЛЬНИКОВ В ПРОЦЕССЕ ИЗУЧЕНИЯ МАТЕМАТИКИ
2.1. Методика по развитию и формированию сравнения у младших
школьников в процессе изучения математики
Сравнение предполагает умение учащихся выполнять следующие действия:
1) выделение свойств у объектов (понятий, отношений);
2) установление общих существенных свойств;
3) выделение основания для сравнения (одного из существенных свойств);
4) сопоставление объектов (понятий, отношений) по данному основанию.
Формирование умения пользоваться приемом сравнения следует осуществлять поэтапно, в тесной связи с изучением конкретного содержания. Целесообразно, например, ориентироваться на такие этапы:
2. выделение признаков или свойств одного объекта;
3. установление сходства и различия между признаками двух объектов;
4. выявление сходства между признаками трех, четырех и более объектов.
Как отмечает М. Иванцив, такими умениями, как выделение свойств предметов, установление общих и отличительных свойств предметов, учащиеся начальных классов владеют хорошо. Но они не знают, что эти умения являются составной частью сравнения, которой необходимо пользоваться во время изучения нового материала. Кроме того, дети не владеют всем набором умений, входящихв состав данного логического приема. Поэтому задача учителя – сформировать у учеников отдельно каждое умение, входящее в состав сравнения; ознакомить с последовательностью их использования.[15, с. 19-20]
Для организации деятельности учащихся, направленной на выделение признаков или свойств следует заготовить специальный набор хорошо знакомых им предметов, в которых они могут выделить те или иные признаки, опираясь на имеющиеся у них представления. Дети первого класса обычно выделяют в предмете два – три свойства, в то время как в каждом предмете бесконечное множества свойств. Для этого им следует показать прием сопоставления данного предмета с другими предметами, обладающими другими свойствами.
Например. Для урока следует заготовить несколько кубиков из различного материала, яблоко, тяжелую гирьку, елочное украшение, прозрачное стекло. Работа начинается с показа ученикам кубика синего цвета.
Учитель: Что вы видите у меня в руках?
Ученики: Кубик.
Учитель: Что можно сказать про этот кубик.
Ученики: Он маленький, синий, сделан из пластмассы.
Учитель: Верно. То, что вы сказали про кубик, и то, что вы записали – это свойства кубика. Какие вы еще свойства кубика вы можете назвать?
Если ребята не могут назвать еще свойств кубика, учитель берет, например, яблоко и показывает детям и т. д. с другими предметами. Дети убеждаются, что свойств у предметов можно назвать очень много.
В процессе работы учитель знакомит детей с понятиями «размер», «форма». Развивается умение выделять признаки и свойства и, ориентируясь на них, учащиеся сравнивают и математические объекты.
· Назови признаки:
1. выражение 3 + 2 (числа 3, 2 и знак «+»);
2. выражение 6 – 1 (числа 6, 1 и знак «– »);
3. равенства х + 5 = 9 (х – неизвестное число, числа 5, 9, знаки «+» и «=»).
С точки зрения операции сравнения все объекты делятся на сравнимые, имеющие какой-либо общий существенный признак, и несравнимые, которые невозможно сравнивать ни по форме, ни по содержанию. Известно, что вторым этапом сравнения является выявление существенных свойств (признаков, сторон) предмета (явления), по которым можно узнать, определить или описать его. В качестве существенных свойств (признаков) могут выступать особенности строения геометрических фигур, свойства функций, неравенств, положение в пространстве геометрических тел, величина, количество и т.д. Велико также разнообразие самих сравниваемых объектов. Это могут быть различные математические операции, чертежи геометрических фигур, свойства уравнений, неравенств. Так, если мы знакомим детей с понятием «квадрат», то нужно показать, что квадраты могут отличаться друг от друга очень многими свойствами: цветом, величиной, расположением в пространстве, обозначением букв и т.д., но у всех них остается неизменными свойства: четыре одинаковых по длине стороны и четыре прямых угла. Если мы изменим хотя бы одно свойство, то уже не сможем назвать эту фигуру квадратом. Таким образом, если изменить несущественные свойства, предмет будет относиться по–прежнему к тому же понятию, а если изменить существенное свойство, предмет становится другим. Здесь также следует показать, что не все общие свойства являются существенными. Так, при работе с выражениями, которые называются суммами 3 + 2; 13 + 7; 12 + 25 общим свойством будет являться состав из двух чисел, который существенным для понятия суммы не является. На этом моменте следует особенно сосредоточить внимание детей, так как они легко принимают любое общее свойство предметов за свойство существенное. Причем эту ошибку допускают даже старшеклассники. Следовательно, надо показать, что любое существенное свойство является общим для данного класса предметов, но далеко не всякое общее их свойство является существенным.
По внешним признакам, доступным для восприятия, дети могут устанавливать сходство и различие между математическими объектами и осмысливать эти признаки с точки зрения различных понятий.
Например
· В чем сходство и различие:
1) выражений: 6 + 2 и 6 – 2; 9 × 4 и 9 × 5; 6 + (7 + 3) и (6 + 7) + 3;
2) чисел: 32 и 45; 32 и 42; 32 и 23; 1 и 11; 2 и 12; 111 и 11; 112 и 12 и т.д.
3) равенств: 4 + 5 = 9 и 5 + 4 + 9; 3 × 8 = 24 и 8 × 3 = 24; 4 × (5 + 3) = 32 и 4 × 5 + 4 × 3 = 32; 2 × (7 × 10) = 210;
4) текстов задач:
Коля поймал 2 рыбки, Петя – 6. На сколько больше поймал рыбок Петя, чем Коля?
Коля поймал 2 рыбки, Петя – 6. Во сколько больше поймал рыбок Петя, чем Коля?
5) геометрических фигур:
![]()
6) уравнений: 3 + х = 5 и х + 3 = 5; 10 – х = 6 и (7 + 3) – х = 6; 12 – х = 4 и (10 + 2) – х = 3 + 1;
7)
![]() вычислительных приемов:9
+ 6 = ( 9 + 1 ) + 5 и 6 + 3 = ( 6 + 2 ) + 1
вычислительных приемов:9
+ 6 = ( 9 + 1 ) + 5 и 6 + 3 = ( 6 + 2 ) + 1
1 + 5 2 + 1
Центральным и наиболее трудным этапом сравнения является выделение оснований для сравнения. Именно способностью выделять эти основания и определяется умение сравнивать. Младшие школьники часто ориентируются не на общий для сравниваемых объектов признак (цвет, форму, длину и т.д.), а на конкретные количественные и качественные показатели этого признака. В силу этого одни ученики считают, что сравнивать, например, по цвету можно только предметы, имеющие один и тот же цвет, но с разной мерой его выраженности («более красный», «менее красный»). Другие, наоборот, считают, что сравнивать предметы по цвету можно только тогда, когда цвет у них разный. Это означает, что учащиеся еще не осознают цвет как общую характеристику предметов, а мыслят лишь на уровне конкретных разновидностей цвета. С этим надо считаться и постепенно учить детей видеть у разноокрашенных предметов, имеющих разную форму и т.д., общее свойство – наличие цвета, формы и т.д.
Если учитель уже научил детей выделять в предметах общие и существенные свойства, то теперь необходимо определить критерии выбора правильных оснований. Во-первых, основаниями для сравнения выступают такие признаки (свойства, характеристики, параметры, условия, причины), по которым изучаемые объекты могут быть сопоставимы; во-вторых, эти признаки должны быть существенными и, в-третьих, основание для сравнения следует устанавливать в отношении однородных предметов и явлений действительности.
Рассмотрим эти требования применительно к обучению математике. Сравнивать следует только однородные предметы (т.е. сопоставимые). Учащимся следует пояснить, что сравнение, например, таких понятий, как «отрезок» и «квадрат», «однозначное число» и «сумма» нецелесообразно. Для определения сопоставимых объектов можно предложить учащимся следующее правило: общее между объектами сравнения можно установить лишь тогда, когда между ними есть какое – то отличие. Разницу между объектами можно установить только при наличии у них определенного сходства.
Например
Чем похожи между собой все:
1) числа: 50, 70, 20, 10, 90 (разрядные десятки);
2) геометрические фигуры (четырехугольники);
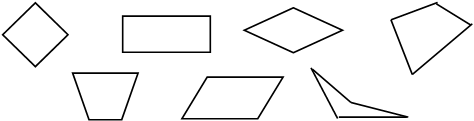
3) Математические записи: 3 + 2, 13 + 7, 12 = 25 (выражения, которые называются суммой).
В обучении младших школьников большая роль отводится упражнениям, которые связаны с переводом «предметных действий» на язык математики. В этих упражнениях они обычно соотносят предметные объекты и символические.
Например,
а) какому рисунку соответствуют записи 2 × 3, 2 + 3?

б) Ка связанно в учетветствует=записи 3 × 4? Если такого рисунка нет, то нарисуй его.

в) Выполни рисунки, соответствующие данным записям: 3 × 7, 4 × 2 + 4 ×3, 3 + 7.
Показателем сформированности приема сравнения является умение детей самостоятельно использовать его для решения различных задач, без указаний: «сравни…, укажи признаки …, в чем сходство и различие…».
Приводим конкретные примеры таких заданий:
1. убери лишний предмет… (при выполнении его школьники ориентируются на сходство и различие признаков.)
2. расположи числа в порядке возрастания: 12,9,7,15,24,2 (для выполнения этого задания ученики должны выявить признаки различия данных чисел.)
3. сумма чисел в первом столбике равна 74. Как, не выполняя сложения во втором и третьем столбиках, найти суммы чисел:
21 22 23
30 31 32
11 12 13
12 13 14
74
4. Продолжи ряды чисел: 2, 4, 6, 8, …; 1, 5, 9, 13 …(Основа установления закономерности (правила) записи чисел – также операция сравнения).
П.М. Эрдниев, исследовавший роль приема сравнения в учебном процессе, рекомендовал применять так называемые двойные правила, которые позволяют не только на слух, но и зрительно разграничить общие и отличительные свойства в сходных формулировках, видеть аналогии, более глубокие связи, облегчающие запоминание. Мы предлагаем использовать, следующие двойственные правила.
![]()
От перестановки ![]()
![]() не меняется;
не меняется;
У ![]() диагонали точкой пересечения
делятся пополам и они равны. [48, с. 200 – 202]
диагонали точкой пересечения
делятся пополам и они равны. [48, с. 200 – 202]
Интерес к сравнению возникает у школьников по мере того, как они осознают его роль в успешном овладении знаниями, начинают понимать, что этот прием имеет общепознавательный характер.
2.2. Дифференцированные упражнения по математике как
средство формирования приёма сравнения
Одна из задач, которая заложена в Государственном стандарте начального образования – ориентация системы образования на детскую личность, её развитие. Личностно-развивающая направленность образования невозможна без дифференциации обучения. Основное назначение дифференцированных заданий в том, чтобы, зная и учитывая индивидуальные отличия в учебных возможностях школьников, обеспечить для каждого из них оптимальный характер познавательной деятельности в процессе обучения. В процессе усвоения знаний и умений один ученик по своим способностям может работать на обязательном уровне подготовки, другой может достичь более высокого уровня, при этом и первый, и второй ученики могут при определённых условиях организации обучения продвинуться в учебе дальше.
Дифференцированное обучение – такой подход, при котором максимально учитываются возможности и запросы каждого учащегося или отдельных групп школьников. Цель дифференцированного обучения – уберечь учеников от возможных пробелов в знаниях, «выровнять» их подготовку, возбудить интерес к учению. Дифференциация на уроке осуществляется через изменение содержания, регулирование трудности и длительности выполнения отдельных заданий, средств методической поддержки учеников в соответствии с их возможностями и подготовленностью к обучению.
Осуществляя дифференцированное обучение, учитель должен:
- иметь четкое представление о том, с какой целью, на каких уроках и как конкретно он будет использовать его;
- изучать и знать общую готовность детей к учебной деятельности, к восприятию конкретного материала;
- предвидеть затруднения, которые могут возникнуть у детей при усвоении нового материала и выполнении дифференцированных заданий.[35,с. 221]
Дифференцированное обучение позволяет эффективно решать вопросы качественного обучения всех детей. Дифференциация на уроке может осуществляться путем изменения содержания, регулирования сложности и длительности выполнения заданий.
Приводим примеры возможной дифференциации обучения приёму сравнения. Отметим, что в исследовании дифференцированное обучение рассматривается в аспекте внутренней дифференциации и предполагает выделение в классе групп учащихся на основе уровней их математической подготовки и сформированности умственных приемов и действий.
К обязательному уровню усвоения мы отнесли упражнения, при выполнении которых школьники ориентируются на сходство и различие признаков. На этом этапе они должны осознать смысл сравнения, уметь объяснять термин «сравнение».
1. В чем сходство и различие:
1) выражений: 11–1 и 11+1; 3(5+6) и 5(6+3);
2) чисел: 10, 20, 30, 40,50; 55 и 555; 110 и 10;
3) равенств: 4 + 5 = 9 и 5 + 4 + 9; 3 × 8 = 24 и 8 × 3 = 24; 4 × (5 + 3) = 32 и 4 × 5 + 4 × 3 = 32; 2 × (7 ×10) = 210;
4) текстов задач: а) В первом ящике 7 кг картофеля, во втором ящике на 3 кг больше, чем в первом. Сколько килограммов картофеля во втором ящике? б) В первом ящике 7 кг картофеля, во втором ящике на 3 кг меньше. Сколько килограммов картофеля во втором ящике?
5) уравнений: 7 + х = 5 и х + 7 = 5; 10 – х = 6 и (7 + 3) – х = 6; 12 – х = 4 и (10 + 2) – х = 3 + 1;
При выполнении упражнений продвинутого уровня ученики должны выявить основания для сравнения, выполнять последовательное (в случае соподчинения объектов), параллельное (рядоположеность объектов), отсроченное (отдалённость связи объектов друг с другом) сравнение.
Реши задачи:
а) Четыре друга спускались с горы н санках. Игорь проехал дальше, чем Роман. Роман проехал меньше, чем Олег, но дальше чем Вадим. Кто проехал меньше всего.
б) Петя выше Кати, Катя выше Оли. Кто выше всех?
в) Сколько шаров необходимо положить на третьи весы, чтобы уравновесить их?

г) Зоя решила больше задач, чем Рита. Алла решила много задач. Кто из девочек решил меньше задач, чем Зоя?
д) Сколько нужно взять слив, чтобы их масса составляла массу одной груши?

? слив
е) Сравни свойства квадрата и прямоугольника.
ж) Сравни примеры, найди общее и сформулируй правило:
1 – 0
2 – 1
3 – 2
4 – 3
(если из последующего числа вычесть предыдущее, то в результате получится 1).
з) Выполни рисунки, соответствующие данным записям: 3 × 7, 4 × 2 + 4×3, 3 + 7.
На этапе выполнения упражнений углублённого уровня ученики самостоятельно используют прием сравнения для различных задач, без указаний: «сравни…, укажи признаки, в чем сходство и различие…».
§ Расположи числа в порядке возрастания: 12, 9, 7, 15, 24, 2 (для выполнения этого задания ученики должны выявить признаки различия данных чисел.)
§ Расположи числа в порядке убывания:45, 34, 2, 17, 38, 3, 58.
§ Сумма чисел в первом столбике равна 74. Как, не выполняя сложения во втором и третьем столбиках, найти суммы чисел:
21 22 23
30 31 32
11 12 13
12 13 14
74
§ Продолжи ряды чисел: 2, 4, 6, 8, …; 1, 5, 9, 13 …
§ Найди лишний ряд: 2 5 8 11 14
![]() 1 4 7 10 13
1 4 7 10 13
3 4 5 6 7
· Какое число пропущено: 3 5 7 9
6 10 14 ?
· Почему, когда мы складываем числа по строчкам или столбикам, получается одно и тоже число:
1 3 4 1 4 3
3 1 3 3 1 4
4 4 1 4 3 1
· Сумма чисел в первом столбике равна 18. Как быстро можно найти сумму чисел, записанных во втором столбике:
3 13
4 14
5 15
![]() Какой
знак (=, <, > ) пропущен: +7 * + 6
Какой
знак (=, <, > ) пропущен: +7 * + 6
2.3. Реализация основных положений опытно-экспериментальной
методики
Экспериментальное теоретическое исследование состояло из двух этапов: констатирующего и аналитико-поискового.
Во время экспериментального исследования систематически анализировались полученные результаты, вносились необходимые коррективы, уточнялась методика.
При проведении экспериментального исследования использовались такие эмпирические методы:
- анализ отобранного программного материала, на котором можно реализовать проблему формирования приема сравнения младших школьников;
- анализ методов, структуры, форм организации по формированию приема сравнения младших школьников;
- изучение психолого-педагогической, методической, философской литературы, анализ накопленного опыта работы учителей по проблеме формирования приема сравнения в начальной школе;
- изучение результатов деятельности младших школьников с целью определения уровня знаний и умений младших школьников при изучении отдельных тем.
Цель эксперимента состояла в выяснении содержания, структуры, приемов и форм организации обучения сравнению в начальной школе, что способствовало бы повышению качества всей математической подготовки учащихся начальной школы, а также повлияло на уровень умственного развития учащихся.
На этом этапе изучалась психолого-педагогическая, методическая литература; анализировался накопленный опыт работы учителей начальных классов г. Евпатории; проводился эксперимент на базе средней школы № 6 г. Евпатории.
По результатам диагностики был определен начальный уровень сформированности умственного приема сравнения. Работа состояла из двух тестовых заданий.
На этом этапе в эксперименте участвовали учащиеся 1 класса средней общеобразовательной школы №6 г. Евпатории.
Первый тест «Исключение понятий» предназначен для исследования умения сравнивать, анализировать и классифицировать.
Обследуемым предлагался бланк 17 рядами слов. В каждом ряду четыре слова объединены общим родовым понятием, а пятое к нему не относится. Испытуемые должны найти эти слова и вычеркнуть их.
1. Василий, Фёдор, Семён, Иванов, Пётр.
2. Дряхлый, маленький, старый, изношенный, ветхий.
3. Скоро, быстро, поспешно, торопливо, постепенно.
4. Ненавидеть, презирать, негодовать, возмущаться, понимать.
5. Тёмный, светлый, голубой, яркий, тусклый.
6. Гнездо, нора, курятник, сторожка, берлога.
7. Неудача, волнение, поражение, провал, крах.
8. Успех, удача, выигрыш, спокойствие, неудача.
9. Ботинки, сапоги, шнурки, валенки, тапочки.
10.Молоко, сыр, сметана, сало, простокваша.
11.Глубокий, низкий, светлый, высокий, длинный.
12.Хата, шалаш, дым, хлев, будка.
13.Токарь, учитель, врач, книга, космонавт.
14.Секунда, час, год, вечер, неделя.
15.Смелый, храбрый, решительный, злой, отважный.
16.Карандаш, ручка, маркер, фломастер, чернила.
17.Стол, стул, кровать, пол, шкаф.
Тест “Аналогии” использовался для определения степени развития логического мышления, в частности умения сравнивать и находить общие признаки у различных объектов (методика предложена Ю. З. Гильбухом).
Материал:
Ручка (или карандаш) и следующие четыре задания:
1. Отец – сын,
мать –
(жена, девочка, дочь, сестра)
2. Страницы – книга,
ветки –
(чтение, листья, буквы, дерево)
3. Начало – конец,
первый –
(второй, середина, начинать, последний)
4. Ложка – металл,
тетрадь –
(ученик, ручка, обложка, бумага)
Инструкция для взрослого:
Тестирование можно проводить как индивидуально, так и с группой детей. Ребенку предлагается бланк с заданиями и дается инструкция. Затем необходимо обсудить выполнение следующих пробных заданий:
1. Автомобиль – бензин,
Троллейбус –
(керосин, электричество, рельсы, провода)
2. Курица – зерно,
корова –
(теленок, рога, трава, масло)
Если ребёнку трудно выполнить это задание, необходимо использовать приём наводящих вопросов: «Для чего автомобилю нужен бензин?» («Для того, чтобы ездить»), «А что необходимо троллейбусу для его работы?» («Электричество, ток»). Обязательно сделайте обобщающий вывод: «Между словами «автомобиль» и «бензин» существует связь – машина работает на бензине. Следовательно, к слову «троллейбус» подходит слово «электричество», так как между этими словами существует такая же связь, как между словами «автомобиль – бензин». Напомните, что подчеркнуть надо именно слово «электричество».
В задании №2 нужно проверить, понимает ли ребенок, что необходимо подчеркнуть слово «трава», так как курица клюет зерно, а корова ест траву.
Инструкция для ребёнка:
Каждое задание состоит из двух пар слов. Между первой парой слов существует определённая связь. Такая же смысловая связь объединяет вторую пару слов. Однако известно только одно из этой пары. Второе надо выбрать из тех, которые написаны ниже в скобках. Подчеркните это слово и переходите к следующему заданию.
Оценка результатов:
Регистрируемый показатель – количество правильных ответов. За каждый правильный ответ начисляется 1 балл, за неправильный – 0 баллов.
Ключ: 1. Дочь.
2. Удовлетворение.
3. Дерево.
4. Последний.
Высокий уровень – 4 балла.
Средний уровень – 3 балла.
Низкий уровень – 0–2 балла.
В результате были установлены следующие показатели сформированности приема сравнения у школьников (см. табл. 2.1.).
Табл.2.1.
Уровни сформированности приема сравнения
| Высокий уровень | Средний уровень | Низкий уровень | |
| 1. | 34 % | 46 % | 19 % |
| 2. | 40% | 38% | 21% |
Из таблицы видно, что не все учащиеся владеют умственным приемом сравнения. Было выявлено 3 группы первоклассников, различающихся по степени владения операцией сравнения. Высокий уровень сформированности приема сравнения наблюдался примерно у 36% детей, низкий – у 20 %. Это свидетельствует о необходимости дальнейшей работы над развитием умственного приема сравнения. Операция сравнения выполняется самостоятельно не всеми детьми. Однако многие первоклассники в состоянии самостоятельно сопоставлять объекты, выделять в них определенные признаки, находить одинаковые признаки в разных объектах.
Результаты аналитико-поискового этапа обсуждались на заседаниях Студенческого Научного Общества, в работе кружка “Актуальные вопросы методики начального обучения” Крымского государственного гуманитарного института.
По результатам констатирующего этапа был сделан вывод о необходимости и значимости сравнения, направленного на развитие их умственной деятельности и повышения качества общей математической подготовки за курс начальной школы.
ЗАКЛЮЧЕНИЕ И ВЫВОДЫ
1. В ходе исследования состояния проблемы в психолого-педагогической теории и практике школьного обучения, анализа психолого-педагогической литературы по проблеме исследования было установлено, что сравнение как методический прием применяется во многих методических и психологических исследованиях. Но сам процесс сравнения, его становление, особенности младших школьников, обучающихся в общеобразовательной школе, мало изучены. Остаётся ещё нераскрытым, как овладевают школьники самой операцией сравнения. Ошибочным с точки зрения современной психологии и дидактики является утверждение о том, что овладение самим содержанием курса математики автоматически формирует мышление школьников. Необходимо специально учить умению мыслить, давать учащимся знания о содержании и последовательности умственных действий обеспечивающих усвоение курса математики. Если не формировать приём, то у многих учащихся он останется на житейском уровне, они не смогут обоснованно и произвольно использовать его как познавательное средство. Математика дает реальные предпосылки для развития логического мышления. Задача учителя – полнее использовать эти возможности при обучении.
2. Были выявлены предмет, содержание, цель, структура и функции умственного приема сравнения, установлены его место и роль в процессе обучения математики. Сравнение как приём применяется очень широко. Его можно использовать практически на всех этапах познания в процессе обучения: при восприятии нового материала, его осмыслении, уточнении и обогащении, систематизации и обобщении, применении в разных сферах. Сформированный прием сравнения позволяет приступить к целенаправленному формированию умения обобщать.
3. При обучении младших школьников сравнению, необходимо научить их выделять признаки и свойства у объектов, устанавливать сходство и различие между признаками, выделять основания для сравнения, причем работа должна вестись целенаправленно, из урока в урок, во взаимосвязи с формированием других умственных приемов. Показателем сформированности приема сравнения является самостоятельное применение его для решения различных задач, без указаний: «сравни…, укажи признаки…, в чем сходство и различие…»
4. Велась работа по обобщению опыта работы учителей, личного опыта сравнительной деятельности при обучении математике. С учетом этого, а также на основе данных В. Ф. Паламарчук была разработана ориентировочная программа по развитию и формированию умственного приема сравнения у детей младшего школьного возраста, также разноуровневые задания для развития приема сравнения.
5. В результате проверки сформированности приема сравнения у учащихся в процессе опытно-экспериментальной работы было установлено, что не все учащиеся владеют данным приемом. Уровень выполнения операции сравнения в определенной мере связан с уровнем успеваемости детей, как правило успешнее учатся те дети, у которых уровень выполнения операции сравнения достаточно высок. Однако полного соответствия между школьной успеваемостью и использованием сравнения не замечено. В группе учащихся, показавшим высокий уровень, были разные по успеваемости дети, что можно объяснить особенностями индивидуального интеллектуального развития детей.
Полученные экспериментальные материалы показывают, что у младших школьников можно и необходимо более интенсивно развивать умственный прием сравнения.
6. Дальнейшая работа по исследованию развития и формирования умственного приема сравнения может продолжаться в направлении изучения механизма переноса умения сравнивать не только на уроках математики, но и при изучении других школьных предметов.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Баринова О. Дифференцированное обучение решению математических задач // Начальная школа. – 1999.– № 2.– с. 41.
2. Богданович М. В. Методика математики на межі тисячоліття.// Початкова школа. – 1999. – № 7. – с.6
3. Богданович М. В., Козак М. В., Король Я. А. Методика викладання математики в початкових класах: Навч.посібник. – К.: А.С.К., 1998.– 352с.
4. Возрастная и педагогическая психология: Учебник для студентов педагогических институтов / Под ред. Петровского А.В. – 2–е изд., испр. и доп. – М.: Просвещение, 1979. – 288 с.
5. Глузман Н.А. Формирование обобщенных приемов умственной деятельности у учителей начальных классов: Учеб. пособие. – Ялта: КГГИ, 2001. – 95 с.
6. Глузман Н.А. Формирование приемов умственной деятельности у младших школьников. – Ялта: КГГИ, 2001. – 34 с.
7. Давыдов В.В. Проблемы развивающего обучения. – М.: Педагогика, 1986.
8. Державна національна доктрина. Затв. Указом Президента України від 17 квітня 2002 р. № 347 // Освіта, – 2002. – № 26
9. Державна національна програма «Освіта. Україна XXI століття”. Затв. постановою Кабінету Міністрів України від 3 грудня 1993, № 896 // Освіта, – 1993. – № 44–46
10. Державний стандарт початкової загальної освіти. Затв. постановою Кабінету Міністрів України від 16.11.2000р. №1717// Поч. школа. – 2001. – № 1. – с. 28.
11. Жукова С. Розвиток логічного мислення учнів початковіх класів шляхом вивчення формальної логіки // Початкова школа. – 2001. – № 2. – с. 47.
12. Закон України “Про внесення змін і доповнень до Закону Української РСР “Про освіту”. – К.: Генеза. – 1996.– 36 с.
13. Захарова А.М. Математика. Первый класс. Методические рекомендации для учителя. Программа развивающего обучения. – Харьков: Центр инноваций, 1994. – 62 с.
14. Истомина Н.Б. Методика обучения математике в начальных классах: Учеб. пособие для студ. сред. и высш. пед. учеб.заведений. – 2–е изд., испр. –М.: Издательский центр «Академия», 1998.–288с.
15. Іванців М. Порівняння на уроках математики. // Початкова школа.– 1999.– № 1. – с. 19 – 20.
16. Кабанова–Меллер Е.Н. Формирование приемов умственной деятельности и умственное развитие учащихся. – М.: Просвещение, 1968. – 288 с.
17. Кондаков Н.И. Логический словарь - справочник, М.: Наука, 1975. – 220 с.
18. Концепція загальної середньої освіти як базової в єдиній системі неперервної освіти. – К.: МО України, 1992. – 177 с.
19. Кочина Л. Математика (программа) // Початкова школа. –2001. – № 8. – с. 75.
20. Крутецкий В.А. Психология математических способностей школьников. – М.: Просвещение, 1968. – 431 с.
21. Кувашова Н. Г. Тематический тестовый контроль по математике в начальной школе. – Волгоград: Учитель, 2002. – 138 с.
22. Леонтьев А. Н. Деятельность. Сознание. Личность. – М.: Политиздат. – 1975.
23. Логачевская С. Диференціация на уроках математики. // Початкова школа. – 1999. № 7. – с. 26
24. Логачевська С. Диференційованне навчання на уроках математики. // Початкова школа. – 2001. – № 5. – с. 18.
25. Махмутов М.И. Организация проблемного обучения в школе. – Книга для учителей. – М.: «Просвещение», 1977
26. Мельник Н. Развитие логического мышления при изучении математики. // Начальная школа. – 1997. № 5. – с. 63
27. Методика начального обучения математике. Учеб. Пособие для студентов пед. Ин–тов по специальности «Педагогика и методика начального обучения»/ Под редакцией Л. Н. Скаткина.– М., «Просвещение», 1972.– 320с.
28. Моро М.И., Пышкало А.М. Методика обучения математике в 1–3 классах. Пособие для учителя. – 2–е изд. – М.: Просвещение, 1978. – 336 с.
29. Муштакова М.В., О. Ю. Шарапова. Система развивающего обучения глазами завуча. // Начальная школа. – 1997. – № 6 .– с. 10 – 15.
30. Немов Р.С. Психология: Учеб. для студ. высш. пед. учеб.заведений: В з кн. – 3-е изд. – М.: Гуманит. изд. центр ВЛАДОС, 1999. – Кн.1. Общие основы психологии. – 688 с.
31. Обучение и развитие: (Экспериментально – практическое исследование) / Под ред. Л.В. Занкова. – М.: Педагогика. 1975. – 440с.
32. Осинская В.Н. Формирование умственной культуры учащихся в процессе обучения математике: Кн. для учителя. – К.: Радянська школа, 1989. – 192 с.
33. Паламарчук В.Ф. Школа учит мыслить. – 2–е изд., доп. и перераб.– М.: Просвещение, 1987. – 208 с.
34. Пентегова Г. А. Развитие логического мышления на уроках математики // Начальная школа. – 2000. – № 11. – с. 74.
35. Подласый И. П. Педагогика начальной школы: Учебное пособие для студентов пед. колледжей. – М.: Гуманит. Изд. центр ВЛАДОС, 2001. – с. 287.
36. Раев А. И. Управление умственной деятельностью младшего школьника. – Л.: ЛГПИ им. А.И. Герцена, 1976. – 134 с.
37. Рубинштейн С. Л. Основы общей психологии. – СПб: Издательство «Питер», 2000.
38. Слепкань З.И. Психолого–педагогические основы обучения математике. – К.: Радянська школа, 1983. – 192 с.
39. Слєпкань З.І. Про державний стандарт з математики // Математика в школі, 1998. – № 1. – с.4–19.
40. Слєпкань З.І., Шкіль М.І., Дороговцев А.Я. та ін. Концепція базової математичної освіти в Україні.– К.: Мін. осв. України, Інститут системних досліджень, 1993. – 31 с.
41. Талызина Н.Ф. Педагогическая психология: Учеб. для студентов сред. пед. учеб. заведения. – 2–е изд., стереотип. – М.: Академия, 1998. – 288 с.
42. Талызина Н.Ф. Формирование познавательной деятельности младших школьников: Книга для учителя. – М.:Просвещение,1988.
43. Типические особенности умственной деятельности младших школьников / под ред. С.Ф.Жуйкова.
44. Тихонова Н. Задачи в развивающем обучении математике // Начальная школа. – 1998. – №7 – с. 51
45. Укурглева Т.А. Актуализация резервов мыслительных операций при обучении математике // Начальная школа. – 1999. – № 2. – с. 50.
46. Фридман Л.М. Психолого–педагогические основы обучения математике в школе. – М.: Просвещение, 1983. – 160 с.
47. Чуприкова Н.И. Умственное развитие и обучение: психологические основы развивающего обучения. – М.: Столетие, 1995. – 189 с.
48. Эрдниев П.М., Эрдниев Б.П. Обучение математике в школе: Книга для учителя. – 2 изд., испр.и доп. – М.: АО «Столетие», 1996. – 320 с.
49. Якиманская И. С. Развивающее обучение. – М.: Педагогика, 1979. – 144 с.
50. Якиманская И. С. Формирование интеллектуальных умений и навыков. – М.: Высшая школа, 1979. – 88 с.
51. Якиманская И.С. Знания и мышление школьника. – М.: Знание, 1985. – 80 с.
ПРИЛОЖЕНИЯ
СОДЕРЖАНИЕ
ПРИЛОЖЕНИЕ А. КОНТЕНТ-АНАЛИЗ СОДЕРЖАНИЯ И ФУНКЦИЙ СРАВНЕНИЯ В НАУЧНОЙ ЛИТЕРАТУРЕ………...........60
ПРИЛОЖЕНИЕ Б. ПРОГРАММА ПО РАЗВИТИЮ И ФОРМИРОВАНИЮ ПРИЕМА СРАВНЕНИЯ В КУРСЕ НАЧАЛЬНОЙ МАТЕМАТИКИ (1–4 КЛАСС)…………………………………………….61
ПРИЛОЖЕНИЕ В. РАЗНОУРОВНЕВЫЕ МАТЕМАТИЧЕСКИЕ УПРАЖНЕНИЯ НА ФОРМИРОВАНИЯ ПРИЕМА СРАВНЕНИЯ……………62
ПРИЛОЖЕНИЕ Г. СТАТЬИ ПО ПРОБЛЕМЕ ИССЛЕДОВАНИЯ……...65
ПРИЛОЖЕНИЕ А
Контент-анализ содержания и функций сравнения в научной литературе
| М.Н. Шардаков (1951, 1953) | Сравнение – это установление сходства и различия предметов и явлений действительности. |
| С.Л. Рубинштейн (1958) | Сравнение – сопоставляя вещи, явления, их свойства, раскрывает тождество и различия. |
| З.И. Слепкань (1983, 2000) | Сравнение – это умственное действие, направленное на выделение общего и отличного в предметах и явлениях. |
| А.И. Раев (1976) |
Сравнение: · определить, для чего должно быть произведено сравнение, какова его цель; · выделить различные признаки сравниваемых объектов; · определить возможные линии сравнения в соответствии с поставленной целью и обнаруженными признаками; · установить общие признаки по каждой из намеченных линий сравнения; · установить особенные признаки по каждой из намеченных линий сравнения; · определить степень существенности общих и особенных признаков по каждой линии сравнения; · соотнести полученные данные по всем линиям; · сформировать вывод о сходстве и различии данных объектов в соответствии с поставленной целью. |
|
В.Ф. Паламарчук (1979); В.Н. Осинская (1989). |
Сравнение – мыслительная операция, посредством которой устанавливаются черты сходства и различия между определёнными предметами и явлениями. Две основные формы: 1) противопоставление – уяснение отличительного в предметах и явлениях при выделении существенных признаков и свойств; 2) сопоставление – выделение существенных свойств, общих для ряда объектов. |
| Е.Т. Коробов (1990) | Сравнение – мыслительная операция, при которой устанавливаются сходства и различия между объектами (основанием для сравнения обычно служат существенные признаки сравниваемых объектов). |
| В.Н Брюшинкин (1996) | Сравнение – мыслительное выделение общих признаков предмета и отбрасывание признаков, свойственных только отдельным видам данного предмета. |
| Н.Ф. Талызина (1998) |
Сравнение: - выделение признаков у объектов; - установление общих признаков; - выделение основания для сравнения(одного из существенных признаков); сопоставление объектов по данному основанию. |
| Н.Б. Истомина(1998) | Сравнение – выделение признаков или свойств одного объекта, установление сходства и различия между признаками трёх, четырёх и более объектов. |
ПРИЛОЖЕНИЕ Б
Программа по развитию и формированию приема сравнения в курсе начальной школы (1– 4 класс)
1 класс
Учить соотносить два предмета, картинки по форме, величине, целевому назначению. Соотносить кружочки, счетные палочки. Сравнение проводить на однотипном материале, преимущественно по внешним признакам в одном направлении (отличие или сходство), завершать эмоциональной оценкой детей.
Сравнивая и классифицируя игрушки, знакомые предметы, учебные принадлежности, делать вывод о принадлежности их к общему родовому понятию. Учиться делать элементарный индуктивный вывод из сравнения двух несложных объектов вербального характера, несложных практических действий. Отвечать на ряд вопросов по общей теме.
Накапливать опыт определения и объяснения понятий через практический показ определяемого предмета, указание, описание. Выделять внешние признаки знакомых предметов, явлений. Для облегчения понимания определений использовать наглядность.
2-й класс
Начать выделение существенных и несущественных признаков предметов.
Сопоставлять на однотипном материале два предмета, картинки по количеству, форме, величине, цвету целевому назначению. Сопоставлять числа, геометрические фигуры. Различать существенные и несущественные признаки предметов и на этой основе находить сходство и отличие. Одновременное сравнение производить на основе конкретных признаков в одном направлении с помощью введения третьего, контрастного объекта. Определять последовательность сравнения, понимать его целенаправленность. Завершать эмоциональной и простейшей логической оценкой. На основе умений анализа, выделение главного, сравнения формировать умения элементарного эмпирического обобщения. Сравнивания и классифицируя знакомые однотипные предметы, изображения, подводить их под общее родовое понятие. Сравнение заканчивать элементарным выводом.
Выделять существенные признаки знакомых предметов.
3-й класс
Тренироваться в разделении существенных и несущественных признаков предметов.
Сопоставлять и противопоставлять по конкретным признакам два предмета, геометрические фигуры, простые задачи, примеры и т. д. Учиться последовательности сравнения и его целенаправленности, завершать суждение простым логическим выводом.
На основе сопоставления и противопоставления двух несложных практических, наглядных объектов формулировать обобщения индуктивным путём. Анализируя и сравнивая практические действия и их результаты, делать выводы по данным критериям.
Выделять существенные и несущественные признаки предметов.
4-й класс
Различать существенные и несущественные признаки несложных предметов.
Продолжить формирование умения сравнивать до качественной ступени, за которой идёт обобщение. Учиться полному сравнению с соблюдением его последовательности: определение объекта и цели сравнения; выделение основных признаков; установление отличия и (или) сходства; формулировка выводов. Сравнивать различную по характеру и целевому назначению информацию на основе существенных конкретных и общих признаков. Проводить одновременное, параллельное и отсроченное сравнение двух объектов с введением третьего, контрастного объекта и контробраза. Сопоставлять и противопоставлять явление и факты. Овладевать правилом-ориентиром сравнением.
ПРИЛОЖЕНИЕ В
РАЗНОУРОВНЕВЫЕ МАТЕМАТИЧЕСКИЕ УПРАЖНЕНИЯ ПО ФОРМИРОВАНИЮ ПРИЕМА СРАВНЕНИЯ
1.
 |
Маленькие фигуры раскрась красным карандашом, а большие – синим:
2. Маленькие треугольники раскрась зеленым карандашом, а большие – красным:
3.
 |
Раскрась фигуры, которые не являются четырехугольником:
4.
 |
Обведи кружочком числа, которые стоят между числами 5 и 8:
А) 3, 6, 4, 5, 9, 7, 8;
Б) 6, 1, 7, 9, 4, 0, 3.
5. Среди данных чисел обведи наибольшее:
А) 2, 5, 8, 0, 6, 4;
Б) 7, 9, 3, 1, 5, 6.
6.
 |
Закрась грибочек, который стоит между прямоугольниками:
7. Расставь числа от большего к меньшему:
2, 1, 4, 7, 9, 2.
8. Зачеркни те числа, которые не являются двузначными. Наименьшее двузначное число обведи красным кружочком:
20, 18, 3, 123, 11,13, 4, 8, 24, 10, 35.
9. Сравни суммы в каждой строчке, не выполняя действия, и поставь знак сравнения:
45 + 24 … 24 + 45;
37 + 23 … 38 + 22;
17 + 26 … 25 + 17;
35 + 40 … 38 + 43.
10. Какой пример можно заменить примером на умножение?
А. 5 + 5 + 4 + 5;
Б. 16 – 2 – 2– 2;
В. 12 + 12 + 12 .
11. Найди выражение, значение которого равно значению 7 · 5:
А. 7 + 7 + 7 + 7 + 7;
Б. 7 + 5;
В. 7 · 4 + 4.
12. Сравнить:
4 + 4 + 4 + 4 + 4 … 4 · 5
8 + 8 + 8 + 8 + 8 … 8 · 4
5 + 3 · 5 + 5 + 5 … 5 · 4
13. Соедини 3 любых числа, чтобы их сумма равнялась 40:
10, 11, 12, 13, 14, 15, 16, 17, 18, 19.
14. найди и подчеркни числа, чтобы их сумма равнялась 40:
10, 11, 12, 13, 14, 15, 16, 17, 18, 19.
15. Найди и подчеркни все выражения с ответом 12:
32 – 20
6 + 6
8 + 5
16. Запиши данные числа в порядке
А. Убывания:
75, 18, 24, 31, 90, 52.
Б. Возрастания:
17, 45, 50, 84, 23, 31.
17. Вместо звёздочек поставь знаки “+” и “–” так, чтобы неравенства были верными:
А. 39 – 9 > 30 * 1
Б. 59 – 9 < 50 * 1
18. Вставь пропущенное число так, чтобы все записи стали верными:
![]() 53
+ 31 = 90 –
53
+ 31 = 90 –
![]() 62 + = 45 + 25
62 + = 45 + 25
19. Какое число больше, чем сумма чисел 39 и 11 на 16?
20. Числа записаны в определённом порядке. Продолжи этот ряд:
2, 4, 6, 8, 10…
21. Запиши результаты примеров, не производя вычислений:
6 · 3 = 18 12 · 5 = 60 30 · 3 = 90
3 · 6 = … 5 · 12 = … 3 · 30 = …
22. Сравни величины:
9 дм … 80 см
4 дм 5 см … 54 см.
23. Обведи кружочками:
А) чётные числа:
20, 17, 12, 7, 2, 5, 6, 10, 1, 8, 13, 4, 9, 14, 16.
Б) те числа, которые делятся на 6 без остатка:
6, 13, 18, 22, 28, 30, 36, 44, 48, 54,60.
24. Вставь пропущенные числа:
395, … , … , … , … , 402.
25. В каждой строчке подчеркни наименьшее число:
676 и 639
799800 и 790999
26. Распредели названия единиц измерения в три столбика: Килограмм, квадратный дециметр, метр, грамм, центнер, дециметр, квадратный метр, сантиметр, тонна, миллиметр, квадратный сантиметр.
27. Среди данных обозначений выбери единицы измерения, связанные с движением, и запиши их в три столбика:
28. Укажи верные неравенства:
915 – 236 > 915 – 236 648 : 3 > 648 : 2
915 – 236 > 915 – 237 648 : 3 < 648 : 2
29. Среди данных выражений подчеркни уравнения:
В – 4 = 500 125 + 75 = 200 у + 18 = 948
85 – х > 70 159 – 104 = 155
ПРИЛОЖЕНИЕ Г
СТАТЬИ ПО ПРОБЛЕМЕ ИССЛЕДОВАНИЯ
Развитие умственного приема сравнения у младших школьников в процессе решения разноуровневых упражнений по математике
Буканова Н.А., студентка 41 – ЕДН
Руководитель Глузман Н.А.
В новой концепции образования приоритетными целями являются развивающие. Рассматривая развивающие возможности математики, в большей степени говорят о развитии логического мышления. И это не случайно: математика имеет широкие возможности для умственного развития учеников благодаря своей системе исключительной ясности и точности понятий выводов и формулировок. Ошибочным с точки зрения современной психологии и дидактики является утверждение о том, что овладение самим содержанием курса математики автоматически формирует мышление школьников. Необходимо специально учить умению мыслить, давать учащимся знания о содержании и последовательности умственных действий, обеспечивающих усвоение курса математики. Однако конкретной программы логических приемов мышления, которые должны быть сформированы при изучении данного предмета, пока нет. В результате работа над развитием логического мышления школьников идет без знания системы необходимых приемов, без знания их содержания последовательности формирования. Это приводит к тому, что большинство учащихся не овладевают основными приемами мышления даже в старших классах школы, а эти приемы необходимы уже младшим школьникам: без них не происходит полноценного усвоения материала.
К числу фактов, определивших выбор темы нашего исследования, относится также недостаточная научная разработанность данной проблемы. Анализируя подходы и концепции, сложившиеся в теории и практике умственного развития, следует отметить исследования, посвященные формированию содержательных обобщений у детей (В.В.Давыдов, В.П.Иржавцева В.А.Крутецкий, В.Н.Осинская, В.Ф.Паламарчук, Л.Я.Федченко, С.А.Фокина, В.П.Хмель,), развитию компонентов мышления, методикам формирования приемов умственной деятельности у школьников (Л.В.Занкова, Н.Б.Истоминой, Е.Н.Кабанова-Меллер, Н.Н.Поспелова, В.И.Решетникова, З.И.Слепкань, Н.Ф.Талызиной, М.Н.Шардакова), формированию алгоритмов, способов формирования мышления учащихся средней школы (В.М.Косатая, Л.Н.Ланда, И.С.Якиманская), но развитие и формирование отдельных умственных приемов в условиях дифференцированного обучения младших школьников еще не нашла своего места в содержании математики начальных классов.
Анализ учебников и программ начальной школы показывает, что прием сравнения необходим учащимся уже в первом классе. Вместе с тем, пишет Талызина Н.Ф., если его не сделать предметом специального усвоения младшими школьниками, то он оказывается не усвоенным большинством учащихся до конца учебного года, что значительно отражается на дальнейшей успеваемости в средних классах.
Изложенное выше обусловило выбор темы исследования «Формирование умственного приема сравнения у младших школьников в процессе решения дифференцированных упражнений по математике».
Исследованием роли сравнения в учебном процессе и разработкой методики формирования этого приема занимались многие психологи, дидакты, методисты–математики ( Г.И. Каганяк, Г.С, Костюк, В.Ф. Паламарчук, В.Н. Осинская, Н.Ф. Талызина, М.Н. Шардаков, П.М. Эрдниев и др.). В своих работах они выделяют сравнение как основу любой умственной деятельности. Так, Д.Н. Богоявленский, Н.А. Менчинская отмечают, что сравнение – обязательное условие всякой абстракции и всякого обобщения. Оно также необходимо при аналогии и классификации. К.Д. Ушинский неоднократно подчеркивал, что сравнение есть основа всякого понимания и всякого мышления.
Сравнение – это прием умственной деятельности учащихся, предполагающий установление сходства или различие между объектами изучения.
Сравнение предполагает умение учащихся выполнять следующие действия:
5) выделение свойств у объектов (понятий, отношений);
6) установление общих существенных свойств;
7) выделение основания для сравнения (одного из существенных свойств);
8) сопоставление объектов (понятий, отношений) по данному основанию.
При рассмотрении сущности приема сравнения нужно уметь определять способы, уровни сравнения,а также и требования предъявляемыми к правильному сравнению. Уровни приема сравнения следующие:
Частичное сравнение – установление только общего, сходного свойства (сопоставление) или только общего, отличительного (противопоставление) в однородных объектах с определенной целью. Полное сравнение – установление существенного общего (сопоставление) и несущественного отличительного (противопоставление) в однородных объектах с определенной целью.
Комплексное сравнение – сопоставление и противопоставление различных объектов или их элементарных частей по разнородным основаниям.
Сравнение можно осуществить различными способами (параллельно, последовательно, отсроченно). Параллельное сравнение – одновременное изучение взаимосвязанных понятий, теорем, задач, при изложении материала укрупненными блоками. Последовательное сравнение – новый объект сравнивается с раннее изученным. Отсроченное сравнение – сравнение объектов значительно удаленных по времени изучения.
Отметим также, что важным методическим приемом в формировании приема сравнения является составление сравнительных таблиц, схем. При выполнении можно отрабатывать все действия приема сравнения и способы его проведения. Например, сравнение может быть односторонним (неполным, по одному признаку) и многосторонним (полным по всем признакам); поверхностным и глубоким; непосредственным и опосредованным.
Формирование умения пользоваться эим приемом следует осуществлять поэтапно, в тесной связи с изучением конкретного содержания. Целесообразно, например, ориентироваться на такие этапы:
5. выделение признаков или свойств одного объекта;
6. установление сходства и различия между признаками двух объектов;
7. выявление сходства между признаками трех, четырех и более объектов.
Одна из задач, которая заложена в Государственном стандарте начального образования – ориентация системы образования на детскую личность, её развитие. Личностно-развивающая направленность образования невозможна без дифференциации обучения. Основное назначение дифференцированных заданий в том, чтобы, зная и учитывая индивидуальные отличия в учебных возможностях школьников, обеспечить для каждого из них оптимальный характер познавательной деятельности в процессе обучения. В процессе усвоения знаний и умений один ученик по своим способностям может работать на обязательном уровне подготовки, другой может достичь более высокого уровня, при этом и первый, и второй ученики могут при определённых условиях организации обучения продвинуться в учебе дальше. Приводим примеры возможной дифференциации обучения приёму сравнения.
К обязательному уровню усвоения мы отнесли упражнения, при выполнении которых школьники ориентируются на сходство и различие признаков. На этом этапе они должны осознать смысл сравнения, уметь объяснять термин «сравнение».
2. В чем сходство и различие:
6) выражений: 11–1 и 11+1; 3(5+6) и 5(6+3);
7) чисел: 10, 20, 30, 40,50; 55 и 555; 110 и 10;
8) равенств: 4 + 5 = 9 и 5 + 4 + 9; 3 × 8 = 24 и 8 × 3 = 24; 4 × (5 + 3) = 32 и 4 × 5 + 4 × 3 = 32; 2 × (7 ×10) = 210;
9) текстов задач: а) В первом ящике 7 кг картофеля, во втором ящике на 3 кг больше, чем в первом. Сколько килограммов картофеля во втором ящике? б) В первом ящике 7 кг картофеля, во втором ящике на 3 кг меньше. Сколько килограммов картофеля во втором ящике?
10) уравнений: 7 + х = 5 и х + 7 = 5; 10 – х = 6 и (7 + 3) – х = 6; 12 – х = 4 и (10 + 2) – х = 3 + 1;
При выполнении упражнений продвинутого уровня ученики должны выявить основания для сравнения, выполнять последовательное (в случае соподчинения объектов), параллельное (рядоположеность объектов), отсроченное (отдалённость связи объектов друг с другом) сравнение.
Реши задачи:
а) Четыре друга спускались с горы на санках. Игорь проехал дальше, чем Роман. Роман проехал меньше, чем Олег, но дальше чем Вадим. Кто проехал меньше всего.
б) Петя выше видит Кати, Катя выше Оли. Кто выше всех?
в) Сколько шаров необходимо положить на третьи весы, чтобы уравновесить их?

г) Зоя решила больше задач, чем Рита. Алла решила много задач. Кто из девочек решил меньше задач, чем Зоя?
§ Сравни свойства квадрата и прямоугольника.
§ Сравни примеры, найди общее и сформулируй правило:
1 – 0
2 – 1
3 – 2
4 – 3
(если из последующего числа вычесть предыдущее, то в результате получится 1)
На этапе выполнения упражнений углублённого уровня ученики самостоятельно используют прием сравнения для различных задач, без указаний: «сравни…, укажи признаки, в чем сходство и различие…».
§ Расположи числа в порядке убывания: 45, 34, 2, 17, 38, 3, 58.
§ Найди лишний ряд: 2 5 8 11 14
![]() 1 4 7 10 13
1 4 7 10 13
3 4 5 6 7
Какое число пропущено: 3 5 7 9
6 10 14 ?
Почему, когда мы складываем числа по строчкам или столбикам, получается одно и тоже число:
| 1 | 3 | 4 | 1 | 4 | 3 |
| 3 | 1 | 3 | 3 | 1 | 4 |
| 4 | 4 | 1 | 4 | 3 | 1 |
Сумма чисел в первом столбике равна 18. Как быстро можно найти сумму чисел, записанных во втором столбике:
3 13
4 14
5 15
Какой знак ( =, <, > ) пропущен: ™ –7 * ™ +6
Практически все рассмотренные выше математические упражнения могут освоить и выполнить учащиеся начальных классов, если учитель постоянно будет проводить соответствующую работу, начиная с 1 класса. В методическом плане использование приема сравнения помогает:
8. более глубоко осознать смысл того или иного математического понятия или способа действия;
9. научить младших школьников сознательно отделять существенные признаки от несущественных;
10. доступнее и нагляднее показывать логическую структуру математических суждений.
Список использованной литературы
1. Державний стандарт початкової загальної освіти. Затв. постановою Кабінету Міністрів України від 16.11.2000р. №1717// Поч. школа. – 2001. – № 1. – с. 28
2. Іванців М. Порівняння на уроках математики. // Початкова школа.– 1999.– № 1. – с. 19.
3. Истомина Н.Б. Методика обучения математике в начальных классах: Учеб. пособие для студ. сред. и высш. пед. учеб.заведений. – 2–е изд., испр. –М.: Академия, 1998.–288с.
4. Талызина Н.Ф. Педагогическая психология: Учеб. для студентов сред. пед. учеб. заведения. – М.: Академия, 1998. – 288 с.
| Развитие логического мышления учащихся при решении задач на построение | |
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ БЛАГОВЕЩЕНСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДПГОГИЧЕСКИЙ УНИВЕРСИТЕТ Физико-математический факультет ... Математическое образование представляет собой сложный процесс, основными целевыми компонентами которого являются: а) усвоение школьниками системы математических знаний; б ... Отметим, что пассивность мышления является одной из основных причин слабого математического развития некоторых школьников и, в частности, формального усвоения содержания обучения ... |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Обогащение словарного запаса на уроках развития речи в младших классах ... | |
|
Дипломная работа. Тема: " Обогащение словарного запаса на уроках развития речи в младших классах вспомогательной школы." Содержание: 1. Введение.. Формирование и развитие у младших школьников перечисленных умений и определяет содержание орфоэпической работы в начальных классах, того минимума, который является обязательным для ... Умение истолковать семантику знакомого слова имеет важное значение как для его усвоения, так и для развития лингвистического мышления учащихся. |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| ... устранению дислексии у детей младшего школьного возраста с ОНР | |
|
РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ им. А.И.ГЕРЦЕНА Факультет коррекционной педагогики Кафедра логопедии Дипломная работа Анализ ... Необходимость выделения поэтапной работы с данной категорией школьников обусловлена тем, что несформированность навыков чтения у младших школьников с дислексией сочетается с ... г) усвоение младшими школьниками слогов как целостных единиц опознания. |
Раздел: Рефераты по педагогике Тип: дипломная работа |
| Проблемное обучение | |
|
Введение. Вся жизнь человека постоянно ставит перед ним острые и неотложные задачи и проблемы. Возникновение таких проблем, трудностей, неожиданностей ... Умение сравнивать - это умение сопоставлять объекты познания с целью нахождения сходства и различия между ними. Формирование умения абстрактно мыслить у школьников в ходе усвоения понятий вовсе не означает, что отпадает необходимость развития умения мыслить наглядно. |
Раздел: Рефераты по педагогике Тип: реферат |
| Формирование учебной мотивации младших школьников с нарушениями ... | |
|
Содержание Введение Глава I Мотивация учебной деятельности как предмет психологического исследования 1.1 Изучение проблемы мотивационной сферы ... Если младшие школьники с нарушением интеллекта, не знают, нужны ли домашние задания или выступают за их отмену, то ученики общеобразовательной школы говорят о том, что домашние ... Они заставляют ребёнка внимательно вдумываться в каждое слово, сравнивать его с другими словами, находить в них сходство и различие, т.е. вырабатывать умение выделять главное ... |
Раздел: Рефераты по психологии Тип: дипломная работа |