Учебное пособие: Основы анализа и синтеза комбинационных логических устройств
Министерство образования Российской Федерации
Российский химико-технологический университет
им. Д. И. Менделеева
Новомосковский институт
Основы анализа и синтеза комбинационных логических устройств
Новомосковск 2008
Министерство образования Российской Федерации
Российский химико-технологический университет
им. Д. И. Менделеева
Новомосковский институт
Основы анализа и синтеза комбинационных логических устройств
Методические указания
Под редакцией В.И.Воробьева
Новомосковск 2008
УДК 681.322
ББК 32.973
О 753
Рецензенты:
кандидат технических наук, доцент кафедры «Автоматизация производственных процессов», НИ РХТУ им. Д.И. Менделеева В. З. Магергут,
кандидат технических наук, доцент кафедры «Автоматизация производственных процессов», НИ РХТУ им. Д.И. Менделеева С. Л. Сидельников.
Составитель: B. C. Прохоров
О 753 Основы анализа и синтеза комбинационных логических устройств: Методические указания / Под редакцией В.И. Воробьева; РХТУ им. Д. И. Менделеева, Новомосковский ин-т; Сост.: B.C. Прохоров.– Новомосковск, НИ РХТУ им Д.И. Менделеева, 2008. - 78 с.
Рассмотрены вопросы анализа и синтеза комбинационных логических устройств. Даются основы математического аппарата и рассматриваются типовые комбинационные схемы.
Ил. 57. Табл. 33. Библиогр.: 8 назв.
УДК 681.322
ББК 32.973
ã Новомосковский институт
РХТУ им. Д. И. Менделеева, 2008
ОГЛАВЛЕНИЕ
Введение
1. Основы математического аппарата анализа и синтеза логических устройств
1.1. Логическая функция
1.1.1. Алгебраическое представление логической функции в совершенной нормальной форме
1.1.2 Графическое представление логической функции в виде Карты Карно (диаграммы Вейча)
1.2 Логические операции
1.3 Аксиомы булевой алгебры.
1.5 Некоторые полезные соотношения
1.6. Минимизация логических функций с помощью карт Карно.
1.7 Аналитические методы минимизации логических функций
1.8 Логический базис
2 Логические элементы, образующие логический базис
2.1 Конъюнктор (элемент И)
2.2 Дизъюнктор (элемент ИЛИ)
2.3......................................... Инвертор (элемент НЕ)
2.4 Элемент Шеффера (элемент И-НЕ)
2.5 Элемент Пирса (элемент ИЛИ-НЕ)
2.6 Функциональная полнота элементов Шеффера (И-НЕ) и Пирса (ИЛИ-НЕ)
3. Взаимное соответствие логической функции и логической схемы
4 Особенности синтеза схем с запрещенными комбинациями
5 Типовые комбинационные схемы
5.1 Мультиплексоры
5.2 Синтез комбинационных схем на мультиплексорах
5.3 Демультиплексоры
5.4 Дешифраторы
5.5 Шифраторы
5.6 Преобразователи кодов
5.7 Сумматоры
5.8 Цифровые компараторы
5.9 Инкрементор
5.9. Коммутатор
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
Введение
В соответствии с типовой программой дисциплины "Схемотехника" подготовка студентов по специальности «Автоматизированные системы обработки информации и управления» ориентирована на изучение цифровых электронных устройств и методов их проектирования с применением систем автоматического проектирования (САПР).
В учебном пособии эти задачи решаются последовательно, начиная с изучения основ математического аппарата и кончая синтезом принципиальных электрических схем цифровых устройств с заданными характеристиками и разработкой для них печатных плат с использованием наиболее распространенной системой проектирования P-CAD. Для лучшего освоения теоретического материала в пособии приведено большое количество примеров. Успешное освоение материала помогает студентам в дальнейшем при изучении более сложных цифровых устройств.
Работа предназначена для студентов впервые проводящих анализ и синтез логических схем, поэтому рассмотрен минимальный круг решаемых при этом простейших задач. Специфические задачи и способы их решения могут быть рассмотрены в пособиях по курсовому и дипломному проектированию, а также в лабораторном практикуме.
Специфика применения САПР при разработке цифровых электронных устройств
Резко сокращаются сроки проектирования изделий при возрастающих требованиях к их качественным характеристикам: Создание любого электронного устройства включает в себя следующие этапы.
1. Формирование технического задания (ТЗ) на разработку, определение структуры и алгоритмов функционирования системы.
2. Разработка схемы электрической принципиальной, перечня элементов и выпуск соответствующей документации.
3. Моделирование или макетирование отдельных узлов или всего устройства в целом.
4. Разработка конструкции печатной платы и выпуск комплекта конструкторской и технологической документации.
5. Подготовка к производству и изготовление печатных плат.
6. Сборка, настройка и регулировка изделия.
В современных условиях выполнение проекта ведется силами сравнительно небольшого коллектива с использованием различных систем автоматического проектирования (САПР). Одной из наиболее распространенных в России САПР является система P-CAD.
Система P-CAD предназначена для проектирования многослойных печатных плат (ПП) вычислительных и радиоэлектронных устройств. В состав P-CAD входят четыре основных модуля - P-CAD Schematic, P-CAD PCB, P-CAD Library Executive, P-CAD Autorouters и ряд других вспомогательных программ.
P-CAD Schematic и P-CAD PCB - графические редакторы, соответственно, принципиальных электрических схем и печатных плат (ПП). Редакторы имеют системы всплывающих меню в стиле Windows, а наиболее часто применяемым командам назначены пиктограммы.
Основное назначение графического редактора P-CAD Schematik – построение принципиальных электрических схем электронных устройств.
В поставляемых вместе с системой P-CAD библиотеках зарубежных цифровых интегральных схем (ИМС) имеются три варианта графики: Normal — нормальный (в стандарте США); DeMorgan — обозначение логических функций; IEEE — в стандарте Института инженеров по электротехнике (наиболее близкий к российким стандартам).
Редактор печатных плат P-CAD PCB может запускаться автономно и позволяет разместить компоненты на монтажно—коммутационном поле для ручной, полуавтоматической и автоматической трассировки проводников. Если P-CAD PCB вызывается из редактора P-CAD Schematic, то автоматически составляется список соединений схемы и на поле ПП переносятся изображения корпусов компонентов с указанием линий электрических соединений между их выводами. Эта операция называется упаковкой схемы на печатную плату. Затем вычерчивается контур ПП, на нем размещаются компоненты и, наконец, производится трассировка проводников.
P-CAD Library Executive - менеджер библиотек. Интегрированные библиотеки P-CAD содержат как графическую информацию о символах и типовых корпусах компонентов, так и текстовую информацию (число секций в корпусе компонента, номера и имена выводов, коды логической эквивалентности выводов и т.д.). Программа имеет встроенные модули: Symbol Editor — для создания и редактирования символов компонентов и Pattern Editor - для создания и редактирования посадочного места и корпуса компонента. Упаковка вентилей компонента, ведение и контроль библиотек осуществляются модулем Library Executive. Модуль имеет средства просмотра библиотечных файлов, поиска компонентов, символов и корпусов компонентов по всем возможным атрибутам.
Разработчик регулярно сталкивается с проблемой создания библиотек компонентов. Как правило; необходимость в этом возникает при создании условных графических изображений компонентов (УГО) в соответствии с действующими стандартами. Для создания библиотечных компонентов используются возможности графических редакторов Schematic и РСВ, а для управления библиотеками — программа Library Executive. P-CAD 2002 имеет интегрированные библиотеки, которые содержат графическую информацию о символах и типовых корпусах компонентов и текстовую упаковочную информацию. Библиотеки, созданные для предыдущих версий P-CAD, переносятся в P-GAD 2002 через текстовый формат PDF.
Первым этапом проектирования любого устройства является формирование технического задания (ТЗ) и разработка структуры системы. Как правило, этим занимается разработчик, который в дальнейшем будет создавать и принципиальную схему устройства. На данном этапе основной является текстовая документация, но она почти всегда сопровождается выпуском структурных или функциональных схем. Конечно, существуют и более удобные для выполнения такого рода схем специализированные графические редакторы, например MS Visio 2000. Они позволяют получить структурную схему возможно качественнее и быстрее, чем редакторы P-CAD Schematic или P-CAD PCB, однако большинству разработчиков гораздо привычнее выполнять структурные и функциональные схемы в той же системе, где будет выполняться и схема электрическая принципиальная. Поэтому рекомендуется выполнять всю конструкторскую документацию в одной среде. Тем более что в P-CAD 2002 возможно использование встроенных механизмов ОС Windows, позволяющих выполнять копирование информации в буфер и ее использование из других приложений, в частности различных текстовых процессоров для оформления документации.
После, выработки технического задания и выпуска функциональной и структурной схем начинается этап создания схемы электрической принципиальной и перечня элементов. Практически все современные разработки немыслимы без предварительного моделирования их работы в одном из пакетов схемотехнического проектирования. Поэтому выполненная в пакете САПР печатных плат схема электрическая принципиальная в идеале, с одной стороны, должна быть пригодна для последующей трассировки платы, а с другой стороны, она же должна передаваться в пакет моделирования. К сожалению, в реальности, как правило, картина иная. Наиболее известным в России пакетом, имеющим одновременно как средства моделирования, так и проектирования печатных плат, является DesignLAB разработки фирмы Microsim. Однако данный пакет не получил широкого распространения при проектировании.
Для моделирования цифровых и аналоговых электронных схем применяют интегрированный пакет MULTISIM (Electronic Workbench Multisim) – редактор схемотехники и SPICE симулятор. Он позволяет анализировать работу электронных схем. Обширная библиотека компонентов включает генераторы сигналов, осциллографы, тестеры, огромное количество полупроводниковых приборов и микросхем разных фирм. Имеет возможность экспорта схемы в программы РСВ – трассировки.
В системе P-CAD 2002 сделан большой шаг вперед. Теперь проблема конвертирования форматов и взаимодействия с пакетами третьих фирм практически решена. В графическом редакторе Schematic имеются необходимые для этого команды
По завершению работы над схемой принципиальной электрический наступает этап проектирования печатной платы. Начинается он с рисования контура печатной платы и размещения компонентов. Для этого в P-CAD предусмотрен графический редактор P-CAD РСВ. Особенностью P-CAD 2002 и является наличие еще одного графического редактора Relay. Данный редактор представляет собой упрощенный вариант редактора РСВ. С помощью Relay возможно выполнить предварительное размещение компонентов, задать необходимые для трассировки зазоры и выполнить трассировку наиболее ответственных цепей.
Ведение проекта в любой САПР невозможно без различных вспомогательных программ, предназначенных для составления отчетов, генерации текстовых конструкторских документов (перечней и спецификаций), коррекции базы данных, автоматической генерации библиотечных компонентов, конвертирования в форматы САПР третьих фирм, анализа электромагнитной совместимости и целостности сигналов и т. д. В частности, в состав P-CAD 2002 включена программа Document Toolbox, предназначенная для расширения возможностей выпуска технической документации без использования чертежных программ типа AutoCAD. Их применение позволяет существенно сократить как временные затраты, так и повысить качество проектирования и сопровождения конструкций аппаратуры.
Следует отметить, что в большинстве случаев для обеспечения удобства электронного оборота конструкторской документации итоговый чертеж или схема выполняются в САПР AutoCAD, поэтому наиболее часто используемой вспомогательной программой является конвертор из формата P-CAD в AutoCAD.
1. Основы математического аппарата анализа и синтеза комбинационных логических устройств
Все устройства, оперирующие с двоичной информацией, подразделяются на два класса:
- комбинационные (дискретные автоматы без памяти).
- последовательные (дискретные автоматы с памятью).
Сигналы на выходах комбинационного устройства однозначно определяются сочетанием сигналов на его входах и не зависят от предыдущих состояний.
Примерами комбинационных устройств могут служить:
1) логические элементы, реализующие логический базис (логические функции И, ИЛИ, НЕ, а также И-НЕ или ИЛИ-НЕ)
2) электронные ключи;
3) мультиплексоры;
4) демультиплексоры и дешифраторы;
5) большинство арифметических устройств и т.д.
Основой анализа и синтеза логических устройств является алгебра логики (булева алгебра).
Связь между входными и выходными сигналами логических устройств устанавливает логическая функция.
1.1 Логическая функция
Функция f(x1,x2,x3,...,xn) называется логической (булевой, переключательной), если она, также как и ее аргументы, может принимать только два значения - “истинно” 1 или “ложно” 0.
Для n логических переменных (аргументов) существует 2n логических комбинаций из 0 и 1.
Например, для n = 2, x1x2 = 00, 01, 10, 11.
Для каждой комбинации
переменных набора логическая функция может принимать значение 0 или 1. Для n
переменных существует ![]() различных
логических функций.
различных
логических функций.
Логическая функция может быть задана:
1) словесно;
2) таблицей истинности;
3) алгебраически;
4) графически.
Пример словесного описания: функция f(x1,x2) принимает значение 1, когда значения переменных равны: x1 = x2. При неравенстве переменных x1¹x2 функция принимает значение 0.
Эту функцию представляют также табл.1.1, которая содержит все 2n возможных наборов значений логических переменных (аргументов) и значения функции, соответствующие каждому из наборов.
Таблица 1.1
Таблица истинности.
|
x1 |
x2 |
f |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
1.1.1 Алгебраическое представление логической функции в совершенной нормальной форме
Различают две формы алгебраического представления логической функции:
совершенная дизъюнктивная нормальная форма (СДНФ);
совершенная конъюнктивная нормальная форма (СКНФ).
Для перехода от табличного представления функции к алгебраическому в виде ее СДНФ каждому i-ому набору переменных ставится в соответствие минтерм (mi) (константа единицы) - конъюнкция переменных, которые входят либо в прямом виде, если значение данной переменной в наборе равно 1, либо в инверсном виде, если значение переменной равно 0. Для n переменных составляют q=2n минтермов: m0, m1,... , mq-1.
Алгебраическое выражение логической функции в форме СДНФ представляют в форме суммы:
![]() ,
,
где fi, mi - значение функции (0 или 1) и минтерм, соответствующий i- ому набору переменных.
Для перехода от табличного представления функции к алгебраическому в виде СКНФ каждому i-ому набору переменных ставится в соответствие макстерм (Mi) - дизъюнкция переменных, которые входят либо в прямом виде, если значение данной переменной равно 0, либо в инверсном виде, если значение переменной равно 1 [1].
Алгебраическое выражение логической функции в форме СКНФ представляют в виде произведения
 ,
,
где fi, Mi - значение функции и макстерм, соответствующий i-ому набору переменных.
Пример 1.1. Логическая функция равнозначность (эквивалентность) для двух переменных представлена табл.1.2.:
Таблица 1.2.
Таблица истинности
|
x1 |
x2 |
f |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Представить эту функцию в алгебраической форме в виде СДНФ и СКНФ.
Решение. 1. Для n=2 переменных составляют q = 2n = 4 минтерма и макстерма, которые вписаны соответственно в 3-ю и 4-ю графы табл.1.3.
Таблица 1.3
Минтермы и макстермы
|
x1 |
x2 |
mi |
Mi |
f |
| 1 | 2 | 3 | 4 | 5 |
| 0 | 0 |
|
|
|
| 0 | 1 |
|
|
|
| 1 | 0 |
|
|
|
| 1 | 1 |
|
|
|
2. Алгебраическое представление логической функции в СДНФ
![]()
![]()
3. Алгебраическое представление логической функции в СКНФ
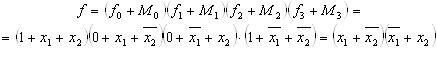
Ускорить процесс нахождения СДНФ и СКНФ можно, если применить другие правила.
СДНФ находят по правилу записи логической функции “по единицам”:
выписывают ряд произведений всех аргументов и соединяют их знаками дизъюнкции; количество произведений должно равняться числу наборов, на которых заданная функция обращается в единицу;
записывают под каждым произведением набор аргументов, на котором функция равна единице, и над аргументами равными 0, ставят знаки отрицания.
Пример 1.2. Представить в СДНФ логическую функцию пяти аргументов f(x1,x2,x3,x4,x5), равную единице на следующих четырех наборах
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 |
Решение. 1. Запишем четыре произведения аргументов, связанных знаком дизъюнкции, и под каждым из них - один из перечисленных наборов
|
x1 x2 x3 x4 x5 Ú x1 x2 x3 x4 x5 Ú x1 x2 x3 x4 x5 Ú x1 x2 x3 x4 x5 |
| 0 0 1 0 1 0 1 1 1 1 1 0 0 0 0 1 1 1 1 1 |
2. Расставляя отрицания над аргументами, равными нулю, получим СДНФ логической функции:
![]() Ú
Ú ![]() Ú
Ú ![]() Ú
Ú ![]()
СКНФ находят по правилу записи переключательной функции “по нулям”:
1) выписывают произведения дизъюнкций всех аргументов с количеством сомножителей, равным числу наборов, на которых заданная функция обращается в нуль;
2) записывают под каждым сомножителем набор аргументов, на котором функция равна нулю, а над аргументами, равными единице ставят знаки отрицания.
Пример 1.3. Представить в СКНФ переключательную функцию четырех аргументов f(x1,x2,x3,x4) , равную нулю на наборах
| 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Решение. 1. Запишем четыре произведения дизъюнкций всех аргументов и под каждым из них один из перечисленных наборов:
|
(x1Úx2Úx3Úx4) × (x1Úx2Úx3Úx4) × (x1Úx2Úx3Úx4) × (x1Úx2Úx3Úx4) |
| 0 0 1 1 0 1 1 1 1 0 0 0 1 1 1 1 |
2. Расставляя знаки отрицания над аргументами, равными единице, получим СКНФ логической функции:
![]()
При выборе совершенной формы записи логической функции следует иметь в виду, что СДНФ является более целесообразной, если число наборов, на которых функция равна 0, превышает число наборов, на которых функция равна 1. В противоположном случае более приемлемой будет СКНФ.
Пример 1.4. Необходимо построить мажоритарную ячейку (ячейку голосования) на три входа, т.е. такую ячейку, у которой сигнал на выходе равен единице тогда, когда большинство входных сигналов равно единице, т.е. он равен единице, когда на двух или трех входах присутствует сигнал единицы, в противном случае выходной сигнал равен нулю [2].
Представить логическую функцию мажоритарной ячейки в виде таблицы истинности и в алгебраическом виде в формах СДНФ и СКНФ.
Решение. 1. Для трех входных сигналов, т.е. для n=3 переменных существует q=2n=23=8 различных комбинаций этих сигналов табл.1.4.
Таблица 1.4
Таблица истинности
|
x1 |
x2 |
x3 |
f |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
2. Для представления логической функции в алгебраическом виде в форме СДНФ нужно представить эту функцию в виде суммы логических произведений аргументов, соответствующих тем строкам таблицы истинности, для которых логическая функция равна единице. При записи этих логических произведений следует брать соответствующий аргумент с инверсией, если этот аргумент в данной строке таблицы равен нулю, и без инверсии, если он равен единице:
![]()
3. Для представления логической функции в алгебраическом виде в форме СКНФ нужно представить эту функцию в виде произведения логических сумм аргументов, соответствующих тем строкам таблицы истинности, для которых логическая функция равна нулю. При записи этих логических сумм следует брать соответствующий аргумент с инверсией, если этот аргумент в данной строке таблицы равен единице, и без инверсии, если он равен нулю:
![]()
Пример 1.5. Полный набор ![]() = 16 логических функций двух
переменных приведен в табл.1.5. Записать алгебраические выражения этих функций
в формах СДНФ и СКНФ.
= 16 логических функций двух
переменных приведен в табл.1.5. Записать алгебраические выражения этих функций
в формах СДНФ и СКНФ.
Таблица 1.5
Полный набор логических функций двух переменных
| Таблица истинности |
Название функции |
Условное обозначение |
Алгебраическое выражение |
|||||
| Функция |
x1 |
0 | 0 | 1 | 1 | |||
|
x2 |
0 | 1 | 0 | 1 | СДНФ | СКНФ | ||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
f0 |
0 | 0 | 0 | 0 | Константа нуль | 0 | ||
|
f1 |
0 | 0 | 0 | 1 | Конъюнкция |
x1 x2 |
||
|
f2 |
0 | 0 | 1 | 0 |
Запрет по x2 |
x1 x1 |
||
|
f3 |
0 | 0 | 1 | 1 |
Тождественность x1 |
x1 |
||
|
f4 |
0 | 1 | 0 | 0 |
Запрет по x1 |
x2 x2 |
||
|
f5 |
0 | 1 | 0 | 1 |
Тождественность x2 |
x2 |
||
|
f6 |
0 | 1 | 1 | 0 | Исключающее ИЛИ Сумма по модулю 2 |
x1 |
||
|
f7 |
0 | 1 | 1 | 1 | Дизъюнкция |
x1 Ú x2 x1 + x2 |
||
|
f8 |
1 | 0 | 0 | 0 | Стрелка Пирса |
x1 ¯ x2 |
||
|
f9 |
1 | 0 | 0 | 1 | Равнозначность |
x1 ~ x2 |
||
|
f10 |
1 | 0 | 1 | 0 |
Инверсия x2 |
|
||
|
f11 |
1 | 0 | 1 | 1 |
Импликация от x2 к x1 |
x2 ® x1 |
||
|
f12 |
1 | 1 | 0 | 0 |
Инверсия x1 |
|
||
|
f13 |
1 | 1 | 0 | 1 |
Импликация от x1 к x2 |
x1 ® x2 |
||
|
f14 |
1 | 1 | 1 | 0 | Штрих Шеффера |
x1 / x2 |
||
|
f15 |
1 | 1 | 1 | 1 | Константа единицы | 1 |
1.1.2 Графическое представление логической функции в виде Карты Карно (диаграммы Вейча)
Логическая функция может быть представлена графически в виде карт минтермов - карт Карно.
Логическую функцию предварительно, исходя из таблицы истинности, приводят к совершенной дизъюнктивной нормальной форме (СДНФ):
![]() ,
,
Где fi, mi - значение функции (0 или 1) и минтерм, соответствующий i-ому набору переменных.
Минтерм - конъюнкция переменных, которые входят либо в прямом виде, если значение данной переменной в наборе равно 1, либо в инверсном виде, если значение переменной равно 0.
Минтерм - это простая конъюнкция, в которую входят все аргументы рассматриваемой логической функции [3].
Простой конъюнкцией считается логическое произведение переменных, взятых с отрицаниями или без них, в котором каждая переменная встречается не более одного раза (в простую конъюнкцию не должны входить суммы переменных, отрицания функций двух или нескольких переменных).
После представления функции в СДНФ, следует заполнить прямоугольную таблицу, в которой число клеток равно числу возможных минтермов. Эту таблицу называют диаграммой Вейча или картой Карно. Каждой клетке таблицы ставится в соответствие определенная конъюнкция так, чтобы в соседних клетках (снизу и сверху, слева и справа) конъюнкции отличались не более чем одним сомножителем. Для этого нумерацию столбцов и строк таблицы ведут кодом Грея, количество разрядов которого равно количеству переменных, отведенных для строк и столбцов.
При заполнении таблицы в соответствующую клетку ставится 1, если логическая функция при данном наборе аргументов равна единице(рис.1.1-1.4).
|
x1 x2 |
0 | 1 |
| 0 |
|
|
| 1 |
|
|
Рис.1.1 Карта Карно для логической функции двух аргументов.
|
x1x2 x3 |
00 | 01 | 11 | 10 |
| 0 |
|
|
|
|
| 1 |
|
|
|
|
Рис.1.2 Карта Карно для логической функции трех аргументов.
|
x1x2 x3x4 |
00 | 01 | 11 | 10 |
| 00 |
|
|
|
|
| 01 |
|
|
|
|
| 11 |
|
|
|
|
| 10 |
|
|
|
|
Рис. 1.3 Карта Карно для логической функции четырех аргументов.
|
x1x2x3 x4x5 |
000 | 001 | 011 | 010 | 110 | 111 | 101 | 100 |
| 00 | ||||||||
| 01 | ||||||||
| 11 | ||||||||
| 10 |
Рис.1.4 Карта Карно для логической функции пяти переменных.
Между представлением логической функции в табличной (таблица истинности), алгебраической (в виде СДНФ) и графической (на карте Карно) формах имеется однозначное соответствие. Логическая функция на карте Карно представляется совокупностью клеток, заполненных 1, инверсия этой функции представляется совокупностью пустых клеток (или заполненных 0).
Для логических функций с числом переменных n ³ 6 наглядность карт Карно теряется и поэтому такие функции представляются в виде композиции функции меньшего числа переменных:
![]() ,
,
где x1 - выделяемая переменная;
функции ![]() получаются из функции f
подстановкой значений x1=0 и x1=1.
получаются из функции f
подстановкой значений x1=0 и x1=1.
В качестве выделяемой может использоваться любая переменная. Например,
![]()
![]()
Процесс выделения более простых функций называется декомпозицией. Полученные функции f0 и f1 могут подвергаться дальнейшей декомпозиции.
1.2 Логические операции
Множество логических функций n переменных можно образовать посредством трех основных логических операций:
1) Логическое отрицание (инверсия);
2) Логическое сложение (дизъюнкция);
3) Логическое умножение (конъюнкция).
Более сложные логические преобразования можно свести к указанным операциям [4]. Логические функции подчиняются принципу дуальности (двойственности) - теоремы Де Моргана; согласно которому операции конъюнкции и дизъюнкции допускают взаимную замену, если одновременно поменять логическую 1 на 0, 0 на 1, знак Ú (+) на Ù(×), а Ù(×) на Ú (+), где Ú или + - обозначение операции дизъюнкции; Ù или × - обозначение операции конъюнкции.
1.3 Аксиомы булевой алгебры
Булева алгебра базируется на нескольких аксиомах, из которых выводят основные законы для преобразований с двоичными переменными (табл. 1.6, 1.7)
Таблица 1.6
Аксиомы булевой алгебры
| конъюнкция | дизъюнкция | |
| 0×0=0 | 0+0=0 | |
| 0×1=0 | 0+1=1 | |
| 1×1=1 | 1+1=1 | |
|
x×0=0 | x+0=x |
|
x×1=x | x+1=1 |
|
x×x=x | x+x=x |
|
|
|
Таблица 1.7
Законы булевой алгебры
| Закон булевой алгебры | Конъюнкция | Дизъюнкция |
|
1 |
2 |
3 |
|
Переместительный (коммутативности) |
x1 x2 = x2 x1 |
x1+ x2 = x2 + x1 |
|
Сочетательный (ассоциативности) |
x1 x2 x3 = x1 (x2 x3) = (x1 x2)x3 |
x1+ x2 +x3 = (x1+ x2)+ x3= =x1 +(x2+ x3) |
|
Распределительный (дистрибутивности) |
x1(x2 +x3)= x1 x2 + x1 x3 |
x1+(x2x3)= (x1+x2)(x1+x3) |
| Поглощения |
x1+ x1 x2 = x1 |
x1 (x1+ x2) = x1 |
| Склеивания |
|
|
| Де Моргана (инверсии, дуальности) |
|
|
| Развертывания |
|
|
|
Не полного |
|
|
1.5 Некоторые полезные соотношения
![]()
![]()
![]()
![]()
1.6 Минимизация логических функций с помощью карт Карно
При минимизации логических функций в карте Карно обводят прямоугольными контурами все единицы и затем записывают минимизированную функцию в виде суммы логических произведений, описывающих эти контуры.
При проведении контуров придерживаются правил:
1) контур должен быть прямоугольным;
2) внутри контура должны быть только клетки, заполненные единицами;
3) число клеток, находящихся внутри контура, должно быть целой степенью числа 2, т.е. можно склеивать 1, 2, 4, 8,... членов;
4) одни и те же клетки, заполненные единицами, могут входить в несколько контуров;
5) при проведении контуров самая нижняя и самая верхняя строки таблицы считаются соседними, то же - для крайнего левого и крайнего правого столбцов;
6) число контуров должно быть как можно меньшим, а сами контуры как можно большим.
Пример 1.6. Провести минимизацию логической функции, заданной в форме СДНФ,с помощью карты Карно (рис.1.5).
![]()
|
x1x2 x3 |
00 | 01 | 11 | 10 |
| 0 |
|
1 | ||
|
|
1 | 1 | 1 |
Рис.1.5 Карта Карно.
Решение. С помощью преобразований, выполняемых по законам булевой алгебры, и с учетом объединенных на карте Карно клеток, получают минимизированное выражение (МДНФ) логической функции:
![]()
![]()
![]() ;
;
![]()
![]() ,
,
![]()
![]() .
.
В рассмотренном примере двум клеткам первого объединения соответствуют минтермы, имеющие две общие переменные
![]() .
.
Поэтому дизъюнкция этих
минтермов равна этим двум общим переменным: ![]() .
.
Четырем клеткам второго
объединения соответствуют минтермы имеющие одну общую переменную ![]() :
:
![]()
Дизъюнкция этих минтермов
также равна общей переменной ![]() .
.
Чем больше клеток входит в объединение, тем меньше переменных входит в соответствующий конъюнктивный член, т.е. проще МДНФ.
Процесс получения алгебраического выражения логической функции, представленной на карте Карно, сводится к считыванию объединений клеток. При этом каждое объединение клеток считывают в виде конъюнктивного члена, в который входят переменные или их инверсии, общие для всех минтермов, соответствующих этим клеткам.
Необъединенные клетки считывают в виде записанных в них минтермов.
Число конъюнктивных членов в МДНФ равно сумме объединений и необъединенных клеток.
Пример 1.7. Логическая функция задана табл.1.8
Таблица 1.8
Таблица истинности
|
x1 |
x2 |
f |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Найти СДНФ этой функции, и провести минимизацию с помощью карты Карно.
Решение: 1. Находят минтермы:
|
x1 |
x2 |
mi |
f |
| 0 | 0 |
|
1 |
| 0 | 1 |
|
1 |
| 1 | 0 |
|
0 |
| 1 | 1 |
|
1 |
2. Логическая функция в форме СДНФ:
![]() .
.
3. Карта Карно логической функции (рис.1.6)
|
x1 x2 |
0 | 1 |
|
|
1 | |
| 1 |
|
1 |
Рис.1.6 Карта Карно логической функции
4. Получают МДНФ функции
![]() .
.
Пример 1.8. Минимизировать с помощью карты Карно (рис.1.7) логическую функцию, заданную в форме СДНФ:
![]()
|
x1x2 x3 |
00 | 01 | 11 | 10 |
| 0 |
|
|||
| 1 |
|
1 | 1 |
Рис.1.7 Карта Карно
Решение: МДНФ функции:
![]()
![]() .
.
Пример 1.9. Минимизировать с помощью карты Карно (рис.1.8) заданную в форме СДНФ логическую функцию:
![]() .
.
|
x1x2 x3 |
00 | 01 | 11 | 10 |
| 0 |
|
|
1 |
|
| 1 | 1 | 1 |
Рис.1.8 Карта Карно:
Решение: МДНФ функции:
![]()
![]()
1.7 Аналитические методы минимизации логических функций
Эти методы базируются на применении основных законов булевой алгебры.
Алгоритм получения МДНФ логической функции:
1. Логическая функция представляется в СДНФ. Причем, если она задана таблицей истинности, то представляют путем записи “по единицам”; если она задана алгебраической произвольной дизъюнктивной форме - путем применения операций развертывания, формул Де Моргана и др.
2. В полученном СДНФ проводят все возможные операции неполного склеивания и затем поглощения. В результате получают сокращенную дизъюнктивную нормальную форму, т.е. дизъюнкцию самых коротких из всех возможных элементарных произведений (простые импликанты), входящие в данную логическую функцию.
3. Находят минимальные дизъюнктивные нормальные формы по импликантной матрице.
Импликантная матрица - это таблица, на вертикальные и горизонтальные входы которой записывают соответственно члены СДНФ и простые импликанты заданной логической функции.
Клетки импликантной матрицы, образованные пересечением строк с импликантами и столбцов с поглощательными ими членами СДНФ, отмечают крестиками [5].
МДНФ находят как дизъюнкцию минимального числа импликант, которые совместно накрывают крестиками все колонки импликантной матрицы.
Пример 1.10. Минимизировать логическую функцию:
![]()
Решение: 1. Функция задана в алгебраической форме, применяя операции развертывания
![]()
![]()
получают СДНФ, содержащую шесть членов:
![]()
2. Операции склеивания проводят в следующем порядке:
1) выполняются все возможные склеивания 1-ого члена с остальными;
2) выполняются все возможные склеивания 2-ого члена с остальными, кроме 1-ого;
3) выполняются все возможные склеивания 3-ого члена с остальными, кроме 1-ого и второго и т.д.
Склеиваться могут только те члены, у которых число переменных с отрицаниями отличается на единицу. Результаты склеивания и поглощения:
![]()
![]()
![]()
![]()
![]()
Звездочками отмечают те члены СДНФ, которые поглощаются произведениями, образовавшимися после склеивания.
В рассматриваемом примере поглощаются все шесть исходных членов, поэтому СДНФ заданной функции имеет вид:
![]()
К этому выражению операции склеивания и поглощения применить нельзя, и, следовательно, оно является сокращенной дизъюнктивной нормальной формой логической функции, а его члены - простыми импликантами.
3. Строят для заданной функции импликантную матрицу (табл.1.9)
Таблица 1.9
Импликантная матрица
| Простые | Члены СДНФ | |||||
|
импликанты (минтермы) |
|
|
|
|
|
|
| 1 | 2 | 3 | 4 | 5 | 6 | |
|
|
X | X | ||||
|
|
X | X | ||||
|
|
X | X | ||||
|
|
X | X | ||||
|
|
X | X |
Для получения МДНФ необходимо найти минимальное число импликант, которые совместно накрывают крестиками все столбцы импликантной матрицы:
![]()
Сложность логической функции определяется числом переменных входящих в ее выражение: в заданной функции 14, в минимальной - 9.
Первый алгоритм получения МКНФ логической функции:
1. Логическую функцию представляют в СКНФ. Причем, если она задана таблицей истинности, то ее записывают “ по нулям”; если она задана алгебраически в произвольной конъюктивной форме, то для записи в СКНФ выполняют все возможные операции развертывания.
2. В полученной СКНФ выполняют все возможные операции неполного склеивания и затем поглощения. В результате получают сокращенную конъюнктивную нормальную форму, члены которой являются простыми макстермами.
3. МКНФ находят по макстермной матрице.
Пример 1.11. Логическая функция задана табл.1.10
Таблица 1.10
Таблица истинности
|
x1 |
x2 |
x3 |
f |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Найти МКНФ этой функции.
Решение:
1. Выписывают заданную функцию в СКНФ “по нулям” таблицы истинности:
![]()
2. Проводят операции склеивания и поглощения:
![]()
![]()
![]()
В данном примере поглощаются все четыре члена исходного выражения и, следовательно, СКНФ
![]()
3. Макстермная матрица задана табл.1.11
Таблица 1.11
Макстермная матрица
|
Простые импликанты |
Члены СКНФ | |||
|
|
|
|
|
|
| (макстермы) | 1 | 2 | 3 | 4 |
|
|
X | X | ||
|
|
X | X | ||
|
|
X | X |
4. МКНФ логической функции:
![]() .
.
Второй алгоритм получения МКНФ логической функции:
1. Логическая функция представляется в СДНФ заданной функцией, взятой с отрицанием.
Если функция задана таблицей истинности, то выписывают ряд произведений всех аргументов и соединяют их знаками дизъюнкции; количество произведений должно равняться числу наборов, на которых заданная функция обращается в нуль; под каждым произведением записывают набор аргументов, на которых функция равна нулю, и над аргументами, равными нулю, ставят знаки отрицания. Если функция заданна алгебраически в произвольной форме, то сначала находят ее СДНФ, а затем записывают дизъюнкцию всех произведений аргументов, которые не вошли в СДНФ.Находят МДНФ по рассмотренному выше алгоритму. От полученной МДНФ берут отрицание и, после преобразований по формулам Де Моргана, получают МКНФ.
Пример 1.12. Найти МКНФ, функции заданной табл.1.12
Таблица 1.12
Таблица истинности
|
x1 |
x2 |
x3 |
f |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Решение: 1. СДНФ, взятая с отрицанием:
![]()
2. Результаты склеивания и поглощения:
![]()
![]()
![]()
3. МДНФ, взятая с отрицанием:
![]()
4. Взяв от обеих частей последнего равенства отрицание и применив формулу Де Моргана, получают МКНФ логической функции:
![]() .
.
1.8 Логический базис
Любую логическую функцию можно представить в виде СДНФ или СКНФ, т.е. с помощью соответствующей комбинации простейших логических функций И, ИЛИ, НЕ. Такой набор простейших логических функций называют функционально полным или логическим базисом.
Логический базис называют минимальным, если удаление хотя бы одной из входящих в него функций превращает его в функционально неполный.
Логический базис И, ИЛИ, НЕ не является минмальным, так как с помощью закона дуальности (Де Моргана) можно исключить из логических выражений либо функцию И, либо функцию ИЛИ:
![]()
![]() .
.
В результате получим минимальные базисы: И, НЕ и ИЛИ, НЕ.
2 Логические элементы, образующие логический базис
2.1 Конъюнктур (элемент И)
Конъюнктур - реализует операцию “логическое умножение”. Схема имеет два или больше входов и один выход. На выходе сигнал “1” появляется тогда и только тогда, когда на все входы одновременно воздействуют входные сигналы “1” рис. 2.1.
|
|
Рис.2.1 Условное изображение конъюнктура на функциональных схемах: x1 ,x2,... , xn - входы (минимальное число входов -2); y- выход.
Логика работы конъюнктура на три входа представлена табл.2.1
Таблица 2.1
Таблица состояний конъюнктура
|
x1 |
x2 |
x3 |
f |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Логическое уравнение работы конъюнктура:
![]() .
.
Знаки (×), (L) соответствуют конъюнкции и читаются как союз И.
Если на вход конъюнктура поступают сигналы в разные моменты времени и разной длительности, то сигнал на входе определяется как результат пересечения входных сигналов (рис. 2.2)
|
|
Рис 2.2 Временная диаграмма работы конъюнктура
Таким образом ![]() , где i=1,2,...
,n
, где i=1,2,...
,n
С точки зрения физической реализации конъюнктуры могут быть выполнены на различных “вентильных” компонентах (диодах, транзисторах и др.)
Функцию И реализуют, например, соединенные последовательно замыкающие контакты нескольких реле. Цепь в этом случае будет замкнута только тогда, когда сработают все реле.
2.2 Дизъюнктор (элемент ИЛИ)
Дизъюнктор - реализует операцию "логическое сложение". Схема имеет два или больше входов. На выходе сигнал "1" появляется тогда, когда хотя бы на один вход воздействует сигнал "1"(рис.2.3).
|
|
Рис. 2.3 Условное изображение дизъюнктора на функциональных схемах: х1, х2,...хn - входы (минимальное число входов - два); у - выход.
Логика работы дизъюнктора на три входа представлена табл.2.2
Таблица 2.2
Таблица состояний дизъюнктора
|
х1 |
х2 |
х3 |
у |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Логическое уравнение
работы дизъюнктора: у=х1+х2+х3 или ![]() . Знаки (+), (
. Знаки (+), (![]() ) соответствуют дизъюнкции и читаются как союз ИЛИ. Если
на вход дизъюнктора поступают сигналы в разные моменты времени и разной
длительности, то сигнал на выходе определяется как результат объединения
входных сигналов (рис.2.4).
) соответствуют дизъюнкции и читаются как союз ИЛИ. Если
на вход дизъюнктора поступают сигналы в разные моменты времени и разной
длительности, то сигнал на выходе определяется как результат объединения
входных сигналов (рис.2.4).
|
|
Рис. 2.4 Временная диаграмма работы дизъюнктора.
Таким образом, ![]() .
.
С точки зрения физической реализации дизъюнкторы могут быть выполнены на различных "вентильных" компонентах (диодах, транзисторах и др.). Функцию ИЛИ реализуют, например, содиненные параллельно замыкающие контакты нескольких реле. Цепь в этом случае будет замкнута, если сработает хотя бы одно реле.
2.3 Инвертор (элемент НЕ)
Инвертор - реализует операцию "логическое отрицание". Схема имеет один вход и один выход. На выходе сигнал "1" имеет место в случае, если на входе будет сигнал "0"(рис.2.5).

Рис. 2.5 Условные изображения инвертора на функциональных схемах: Х-вход, У-выход
Логика работы инвертора представлена табл.2.3
Таблица 2.3
Таблица состояний инвертора
| Х | У |
| 0 | 1 |
| 1 | 0 |
Логическое уравнение работы инвертора:
![]()
Уравнение читается: У равняется не Х.
С точки зрения физической реализации наибольшее распространение получили инверторы на транзисторах.
Функцию НЕ реализует, например, размыкающий контакт реле. При срабатывании реле цепь, в которую входит этот контакт, будет размыкаться.
2.4 Элемент Шеффера (элемент И-НЕ)
Элемент Шеффера - реализует операцию логическое умножение с отрицанием. На выходе сигнал "1" имеет место всегда, кроме случая, когда сигналы "1" на всех входах совпадают (рис. 2.6).
|
|
Рис. 2.6 Условное изображение элемента Шеффера на функциональных схемах: х1, х2, хn - входы (минимальное число входов - два); y - выход.
Логика работы элемента Шеффера на три входа представлена табл.2.4
Таблица 2.4
Таблица состояний элемента Шеффера
|
х1 |
х2 |
х3 |
у |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Логическое уравнение работы элемента Шеффера:
![]()
Уравнение позволяет представить логическую схему элемента Шеффера в виде(рис.2.7).
|
|
Рис. 2.7 Представление логической схемы элемента Шеффера в виде последовательного соединения конъюнктора и инвертора.
2.5 Элемент Пирса (элемент ИЛИ-НЕ)
Элемент Пирса - реализует операцию логическое сложение с отрицанием. На выходе сигнал "1" имеет место только в случае, если на всех входах одновременно будет сигнал "0" (рис.2.8).
|
|
Рис. 2.8 Условное изображение элемента Пирса на функциональных схемах: х1, х2, хn - входы (минимальное число входов - два); y - выход.
Логика работы элемента Пирса на три входа представлена табл.2.5
Таблица 2.5
Таблица состояний элемента Пирса
|
х1 |
х2 |
х3 |
у |
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
Логическое уравнение работы элемента Пирса:
![]()
Поэтому логическую схему элемента Пирса можно представить рис.2.8
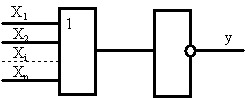
Рис. 2.8 Представление логической схемы элемента Пирса в виде последовательного соединения дизъюнктора и инвертора.
2.6 Функциональная полнота элементов Шеффера (И-НЕ) и Пирса (ИЛИ-НЕ)
Для того чтобы доказать функциональную полноту элемента Шеффера, покажем возможность построения на его основе логических цепей, реализующих простейшие функции НЕ, И, ИЛИ (рис.2.9).
а) Функция НЕ:
|
|
б) Функция И:
|
|
в) Функция ИЛИ:
|
|
Рис.2.9 Способы построения на основе элемента Шеффера простейших функций
То же сделаем для элемента Пирса (рис.2.10).
а) Функция НЕ:
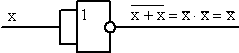
б) Функция И:
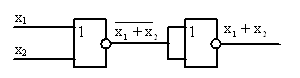
в) Функция ИЛИ:

Рис. 2.10 Способы построения на основе элемента Пирса логических цепей И, ИЛИ, НЕ.
3. Взаимное соответствие логической функции и логической схемы
По заданной логической функции f(х1, х2, х3,...,хn) можно составить электрическую схему, которая будет преобразовывать логические сигналы х1, х2, х3,...,хn согласно указанной функции.
Различают схемы:
1) структурные;
2) функциональные;
3) принципиальные (полные).
Структурная схема определяет основные функциональные части, их назначение и взаимосвязи. Структурная схема концентрирует в себе все наиболее важное и существенное о составе, структуре и функциях электронного устройства (ЭУ). Электронным устройством называют любую совокупность взаимодействующих электрорадиоэлементов, предназначенную для выполнения заданной функции.
Функциональная схема разъясняет процессы, протекающие в отдельных цепях или в целом ЭУ. Она занимает промежуточное место между структурной и принципиальной схемами. Цепи, в которых хотят разъяснить процессы, показывают так же подробно, как и на принципиальной схеме, а другие функциональные части изображают в виде прямоугольников, как и на структурной схеме.
Принципиальная (полная) схема определяет полный состав элементов и связей между ними и дает детальное представление о принципах работы ЭУ.
Существуют два уровня, на которых разрабатывают указанные три вида схем:
1) микроуровень;
2) макроуровень.
На микроуровне разрабатывают схемы для интегральных микросхем (ИМС). Эти схемы создают разработчики ИМС, они входят в состав документации на ИМС и приводятся в справочниках и технической литературе.
К структурным схемам цифровых ИМС относят схемы, на которых представлены ее части, более крупные, чем функциональные элементы. Функциональный элемент - наименьшая единица функциональной структуры, которая при технической реализации может быть выполнена в виде электрической законченной схемы, выполняющей определенную функцию. Структурные схемы разрабатывают для больших (БИС) и сверхбольших (СБИС) интегральных схем. На этом уровне интеграции разработка функциональных схем для использования лишена смысла ввиду их сложности. О правильности функционирования БИС и СБИС судят по значениям логических сигналов на их выходах при тестировании.
Для ИМС среднего (СИС) и малого (МИС) уровня интеграции разрабатывают функциональные схемы. Структурными элементами функциональных схем комбинационных систем являются логические элементы. Логические элементы различаются между собой характером реализуемой функции, числом входов (по числу одновременно действующих переменных), числом выходов и другими признаками. Работа их оценивается только с точки зрения логики, без учета практического воплощения (технической базы, способа питания и т.п.). Структурными элементами функциональных схем последовательных систем (системы с памятью) являются триггеры и логические элементы.
Функции, выполняемые логическими элементами и триггерами, могут быть определены по их условным графическим обозначениям. К функциональным относятся такие схемы, на которых одна из нескольких одинаковых частей показана на уровне логических элементов (и триггеров), и остальные - в виде более крупных структур.
Структурная и функциональная схемы не дают представления о физических процессах в логических элементах. Эти представления для каждой серии ИМС дают принципиальные схемы их базовых логических элементов.
На схемах логические элементы по ГОСТ 2.743-82 "Обозначения условные графические в схемах. Элементы цифровой техники" изображают прямоугольником, в верхней части которого указывают символ функции: & для И; 1 для ИЛИ. Инверторные входы и выходы выделяются кружком у вывода. Выводы питания и общий не показывают.
Рассмотрим порядок составления функциональной схемы (рис.3.1) по заданной логической функции, например,
![]()
1-й этап - получить отрицание от переменных х1, х2, х3.
2-й этап - получить
дизъюнкцию ![]() ,
конъюнкции
,
конъюнкции ![]() и
и
![]() .
.
3-й этап - получить
конъюнкцию х1(![]() ).
).
 |
4-й этап - получить заданную логическую функцию.
Рис. 3.1 Функциональная схема.
Проектирование функциональных схем сводится к последовательным формальным процедурам, которые могут быть реализованы на ЭВМ. Способ соединения логических элементов функциональной схемы определяется последовательностью выполнения логических операций в заданной логической функции. Последовательность выполнения этих операций удобно разбить на ряд этапов. В каждый этап включают те операции, которые можно проводить в произвольной последовательности.
Пример 3.1. Синтезировать в базисе И, ИЛИ, НЕ и в базисе И-НЕ, ИЛИ-НЕ устройство, сигнал на выходе которого равен 1 только в том случае, когда на его двух входах (х1 и х2) действуют различные сигналы (узел неравнозначности, сумматор по модулю два).
Решение: 1. Таблица истинности в соответствии со словесным описанием работы устройства:
|
х1 |
х2 |
f |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
2.Для перехода от табличного представления функции к алгебраическому в формах СДНФ и СКНФ каждому набору переменных ставятся в соответствие минтермы (mi) и макстермы (Mi):
х1 |
х2 |
mi |
Mi |
f |
| 0 | 0 |
|
|
0 |
| 0 | 1 |
|
|
1 |
| 1 | 0 |
|
|
1 |
| 1 | 1 |
|
|
0 |
3. СДНФ функции:
![]() ,
,
где q=2n, n - число переменных.
4. СКНФ функции:
![]() .
.
Применив правило Де
Моргана:![]() ,
получим:
,
получим:
![]()
4. Функциональная схема для функции, представленной в СДНФ, в базисе И, ИЛИ, НЕ (рис.3.2).
|
|
Рис. 3.2 Функциональная схема устройства в базисе И, ИЛИ, НЕ
6. Функциональная схема для функции, представленной в СКНФ, в базисе И, ИЛИ, НЕ (рис.3.3).
|
|
Рис. 3.3 Функциональная схема устройства в базисе И, ИЛИ, НЕ
7. Для использования базиса И-НЕ, ИЛИ-НЕ преобразовывают далее полученные логические функции. Применяют закон двойной инверсии:
![]()
![]()
В соответствии с законами Де Моргана (инверсии; принципа дуальности, двойственности):
![]() ;
;
![]() .
.
8. Функциональная схема для реализации функции f1 (рис.3.4).

Рис.3.4 Функциональная схема для реализации функции f1
9. Функциональная схема для реализации функции f2 (рис.3.5).

Рис.3.5 Функциональная схема для реализации функции f2
Пример 3.2. Синтезировать в базисе И, ИЛИ, НЕ и в базисе И-НЕ, ИЛИ-НЕ устройство, сигнал на выходе которого равен 1, только в том случае, когда на его двух входах (х1, х2) действуют одинаковые сигналы (узел равнозначности).
Решение. 1. Таблица истинности в соответствии со словесным описанием работы устройства:
|
х1 |
х2 |
f |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
2. Определяют минтермы mi и макстермы Mi:
|
х1 |
х2 |
mi |
Mi |
f |
| 0 | 0 |
|
|
1 |
| 0 | 1 |
|
|
0 |
| 1 | 0 |
|
|
0 |
| 1 | 1 |
|
|
1 |
3. СДНФ функции:
![]() .
.
Применив закон Де Моргана, получают:
![]() .
.
4. СКНФ функции:
![]() .
.
В соответствии с законом Де Моргана:
![]() .
.
5. Функциональная схема для f1 (рис.3.6).

Рис.3.6 Функциональная схема для f1
6. Функциональная схема
для ![]() (рис.3.7).
(рис.3.7).

Рис. 3.7
Функциональная схема для ![]()
7. Функциональная схема для f2 (рис.3.8).

Рис. 3.8 Функциональная схема для f2
8. Функциональная схема
для ![]() (рис.3.9).
(рис.3.9).

Рис.3.9 Функциональная
схема для ![]()
Все четыре функциональные схемы логически равноценны.
Пример 3.3. Устройство с четырьмя входами должно работать так, чтобы на выходе появился сигнал 1, когда не менее чем на трех входах будут одновременно сигналы 1. Синтезировать устройство на элементах И, ИЛИ, НЕ.
Решение. 1. Таблица истинности в соответствии со словесным описанием работы устройства:
Таблица 3.1
Таблица истинности
| Номер набора |
х1 |
х2 |
х3 |
х4 |
f |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 2 | 0 | 0 | 1 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 0 |
| 6 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 1 |
| 8 | 1 | 0 | 0 | 0 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 |
| 10 | 1 | 0 | 1 | 0 | 0 |
| 11 | 1 | 0 | 1 | 1 | 1 |
| 12 | 1 | 1 | 0 | 0 | 0 |
| 13 | 1 | 1 | 0 | 1 | 1 |
| 14 | 1 | 1 | 1 | 0 | 1 |
| 15 | 1 | 1 | 1 | 1 | 1 |
2. Запишем СДНФ функции на основе ее единичных наборов:
![]() .
.
3.Для минимизации функции применим карту Карно (рис.3.10).
|
х1х2 х3х4 |
00 | 01 | 11 | 10 |
| 00 | 0 | 0 | 0 | 0 |
| 01 | 0 | 0 |
|
0 |
| 11 | 0 |
|
1 |
1 |
| 10 | 0 | 0 |
1 |
0 |
Рис. 3.10 Карта Карно
4. МНДФ функции:
![]() .
.
5. Функциональная схема устройства (рис.3.11).

Рис.3.11 Функциональная схема устройства
Пример 3.4. Синтезировать мажоритарный элемент на три входа в базисе ИЛИ-НЕ. У такого элемента значение выходного сигнала совпадает с значением большинства входных.
Решение. 1. Таблица истинности в соответствии со словесным описанием работы элемента:
|
x1 |
x2 |
х3 |
у |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
2. СДНФ функции на основе ее единичных наборов:
![]() .
.
3. Для минимизации функции применим карту Карно (рис.3.12).
|
х1х2 х3 |
00 | 01 | 11 | 10 |
|
|
|
0 |
|
|
| 1 | 0 |
|
1 | 1 |
Рис.3.12 Карта Карно
4. МДНФ функции:
![]() .
.
5. МКНФ функции:
![]() .
.
6. Для реализации функции в базисе И-НЕ и в базисе ИЛИ-НЕ преобразуем функцию в соответствии с законом Де Моргана:
![]() ;
; ![]() .
.
7. Функциональная схема для функции f1 в базисе И-НЕ (рис.3.13).
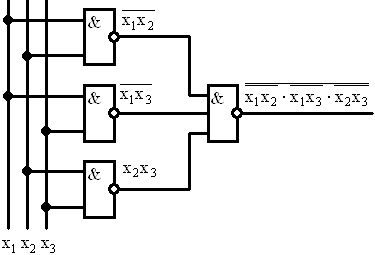
Рис.3.13 Функциональная схема для функции f1 в базисе И-НЕ
8. Функциональная схема для функции f2 в базисе ИЛИ-НЕ (рис.3.14).

Рис.3.14 Функциональная схема для функции f2 в базисе ИЛИ-НЕ
4. Особенности синтеза схем с запрещенными комбинациями
Иногда применяют устройства, закон функционирования которых определен неполностью. В таких устройствах некоторые комбинации сигналов на входы никогда не подаются (запрещены).
Работа устройств с запрещенными комбинациями входных сигналов описывается неполностью определенными логическими функциями, значения которых определены не на всех наборах аргументов.
Нормальная работа устройства с неполностью определенным законом функционирования не нарушится, если произвольно задать значения функции для запрещенных комбинаций аргументов.
Обычно логической функции на запрещенных наборах придают такие значения, при которых она приобретает наиболее простой вид.
При минимизации логической функции безразличные наборы входных переменных в соответствующих клетках карты Карно обозначают знаком Х. В объединения включают те клетки, отмеченные Х, которые дают расширение объединений и уменьшение их количества.
5. Типовые комбинационные схемы
Серии микросхем, выпускаемые промышленностью, содержат широкую номенклатуру элементов, выполняющих не только простейшие логические функции (И, ИЛИ, НЕ, ИЛИ-НЕ, И-НЕ), но и более сложные операции, например, выполняемые мультиплексорами и демультиплексорами, шифраторами и дешифраторами, преобразователями кодов, сумматорами и т.д.
Поэтому не может быть речи о синтезе комбинационных схем только в базисах И, ИЛИ, НЕ, или ИЛИ-НЕ, а также И-НЕ, а следует наиболее полно использовать функциональные возможности всех логических элементов.
Для успешного синтеза цифровых узлов следует знать функционирование типовых комбинационных схем, выпускаемых промышленностью в виде интегральных микросхем, и которые синтезированы, как правило, в логических базисах И, ИЛИ, НЕ, или ИЛИ-НЕ, а также И-НЕ.
5.1 Мультиплексоры
Мультиплексор (коммутатор) - комбинационное многовходовое устройство с одним выходом.
Входы подразделяются на:
1) информационные х1, х2, х3,..., хn;
2) управляющие (адресные) v1, v2, v3,..., vm;
где n - число информационных входов,
m - число управляющих (адресных) входов.
Обычно n=2m.
Код (адрес), поступающий на управляющие входы, определяет один из информационных входов, значение переменной которого передается на выход у.
Адреса представляют в двоичном коде и им присваивают номер j. Каждому адресу с номером j соответствует свой информационный вход xj, сигнал с которого при данном адресе проходит на выход.
Основным назначением мультиплексора является коммутация n=2m входных сигналов на один выход.
В соответствии с назначением составим таблицу истинности для мультиплексора, содержащего, например, четыре информационных входа: х1, х2, х3, х4, которые могут коммутироваться двумя управляющими (адресными) входами (табл.5.1).
Таблица 5.1
Таблица истинности мультиплексора
|
Адресные переменные |
Информационные Переменные |
Выход у |
||||
|
v1 |
v2 |
x1 |
x2 |
x3 |
X4 |
y |
| 0 | 0 | 1 | 1 | |||
| 0 | 1 | 1 | 1 | |||
| 1 | 0 | 1 | 1 | |||
| 1 | 1 | 1 | 1 | |||
| 0 | 0 | 0 | 0 | |||
| 0 | 1 | 0 | 0 | |||
| 1 | 0 | 0 | 0 | |||
| 1 | 1 | 0 | 0 |
Незаполненные клетки соответствуют значениям информационных переменных, не влияющих на значение выходного сигнала у. Так как каждому адресу соответствует свой информационный вход, то таблицу истинности можно представить в виде (табл.5.2).
Таблица 5.2
Преобразованная таблица истинности мультиплексора
|
Адресные переменные |
Информационные переменные |
Выход у |
||||
|
v1 |
v2 |
x1 |
x2 |
x3 |
x4 |
y |
| 0 | 0 |
х1 |
х1 |
|||
| 0 | 1 |
х2 |
х2 |
|||
| 1 | 0 |
х3 |
х3 |
|||
| 1 | 1 |
х4 |
х4 |
Работа мультиплексора описывается при этом логической функцией:
![]() ,
,
а его функциональная схема дана на (рис.5.1).

Рис. 5.1. Функциональная схема мультиплексора.
Функция, реализуемая мультиплексором, в общем виде может быть представлена в виде СДНФ:
![]() .
.
5.2 Синтез комбинационных схем на мультиплексорах
Кроме основного
назначения (коммутация сигналов) мультиплексоры используют для построения
постоянных запоминающих устройств (ПЗУ) объемом 2m+1 бит и для синтеза комбинационных логических схем.
При этом можно синтезировать ![]() различных логических функций от (m+1) логических переменных. Например,
на мультиплексоре с n=4 и m=2 входами реализуется любая логическая
функция от трех переменных, т.к. для трех переменных существует
различных логических функций от (m+1) логических переменных. Например,
на мультиплексоре с n=4 и m=2 входами реализуется любая логическая
функция от трех переменных, т.к. для трех переменных существует ![]() различных функций.
различных функций.
При построении ПЗУ на информационные входы мультиплексора подают не изменяющиеся во времени сигналы 0 и 1. Считывание данных сигналов производится подачей соответствующих сигналов на адресные (управляющие) входы.
В этом случае мультиплексор реализует некоторую наперед заданную функцию, представленную в совершенной дизъюктивной нормальной форме (СДНФ), как следует из представленной выше логической функции мультиплексора.
Основной задачей при синтезе комбинационных логических схем на мультиплексорах является оптимальный выбор переменных, подаваемых на его управляющие (адресные) входы.
Критерием оптимальности выбора адресных переменных может служить количество сигналов 0 и 1, подаваемых при этом на информационные входы.
Правило выбора адресных переменных рассмотрим для двух случаев.
Пусть логическая функция задана табл.5.3
Таблица 5.3
Таблица истинности
|
х1 |
х2 |
х3 |
f |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Выделим из логических переменных переменную х3. Одинаковые комбинации оставшихся переменных х1 х2 представим в виде групп (отделены в таблице истинности двойными горизонтальными линиями).
Выберем в качестве адресных (управляющих) переменных переменные х1 и х2. При коде v1v2=x1x2=00 на выход мультиплексора коммутируется вход Х1. Если на вход Х1 подать переменную х3, то на выходе получим значение логической функции при х1х2=00. Это удобно отразить в табл.5.4
Таблица 5.4
Таблица истинности
Адресные переменные |
Информационные переменные |
Выход | ||||
|
v1 x1 |
v2 x2 |
X1 |
X2 |
X3 |
X4 |
f |
| 0 | 0 |
x3 |
x3 |
|||
| 0 | 1 |
|
|
|||
| 1 | 0 | 0 | 0 | |||
| 1 | 1 | 1 | 1 |
При коде v1v2=x1x2=01 на выход коммутируется вход Х2. В соответствии
с таблицей истинности логической функции, на этот вход следует подать ![]() .
.
При коде v1v2=x1x2=10 на выход коммутируется вход x3. В соответствии с таблицей истинности логической функции, на этот вход следует подать "0".
При коде v1v2=x1x2=11 на выход коммутируется вход x4. В соответствии с таблицей истинности логической функции, на этот вход следует подать "1" (рис. 5.2).
|
|
Рис. 5.2 Пример синтеза комбинационной схемы на мультиплексоре.
На мультиплексорах можно реализовывать совместно две функции. При этом отыскивают те переменные, которые суммарно входят в МДНФ функций наибольшее число раз. Например, заданы МДНФ двух функций:
![]()
![]() .
.
Таблица истинности для них выглядит следующим образом:
|
x1 |
x2 |
x3 |
x4 |
f1 |
f2 |
| 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Если в качестве таких переменных выбрать х3 и х2, то получим следующие таблицы истинности для заданных функций.
Для f1:
|
v1 x3 |
v2 x2 |
X1 |
X2 |
X3 |
X4 |
f1 |
| 0 | 0 |
|
|
|||
| 0 | 1 |
|
|
|||
| 1 | 0 |
|
|
|||
| 1 | 1 |
|
|
Для f2:
|
v1 x3 |
v2 x2 |
Y1 |
Y2 |
Y3 |
Y4 |
f2 |
| 0 | 0 |
|
|
|||
| 0 | 1 | 0 | 0 | |||
| 1 | 0 |
|
|
|||
| 1 | 1 |
|
|
Функциональная схема устройства на сдвоенном четырехканальном мультиплексоре имеет вид рис.5.3.

Рис. 5.3 Применение мультиплексора для реализации совместно двух логических функций.
Пример 5.1. Синтезировать мультиплексор с восемью информационными входами и одним выходом на элементах И, ИЛИ, НЕ.
Решение. 1. Восемь информационных входов могут коммутироваться на один выход с помощью трех адресных входов (n=2m, для n=8, m=3) 2. Таблица истинности для логической функции мультиплексора (табл. 5.5).
Таблица 5.5
Таблица истинности
| Адрес |
Выход y |
||
|
v1 |
v2 |
v3 |
|
| 0 | 0 | 0 |
x1 |
| 0 | 0 | 1 |
x2 |
| 0 | 1 | 0 |
x3 |
| 0 | 1 | 1 |
x4 |
| 1 | 0 | 0 |
x5 |
| 1 | 0 | 1 |
x6 |
| 1 | 1 | 0 |
x7 |
| 1 | 1 | 1 |
x8 |
3. Логическая функция в соответствии с таблицей истинности:
![]()
4. Функциональная схема мультиплексора рис.5.4.

Рис 5.4 Функциональная схема мультиплексора с восемью информационными входами.
5.3 Демультиплексоры
Демультиплексор - комбинационное устройство с одним информационным входом х1, с m управляющими входами (v1...vm) и с n информационными выходами (y1...yn), при этом n=2m.
Основное назначение демультиплексора - распределение сигнала с линии по нескольким каналам (обратное мультиплексору).
Таблица истинности для n=8 и m=3 (табл.5.6)
Таблица 5.6
Таблица истинности для n=8 и m=3
|
v3 |
v2 |
v1 |
y1 |
y2 |
y3 |
y4 |
y5 |
y6 |
y7 |
y8 |
| 0 | 0 | 0 | x | |||||||
| 0 | 0 | 1 | x | |||||||
| 0 | 1 | 0 | x | |||||||
| 0 | 1 | 1 | x | |||||||
| 1 | 0 | 0 | x | |||||||
| 1 | 0 | 1 | x | |||||||
| 1 | 1 | 0 | x | |||||||
| 1 | 1 | 1 | x |
где х принимает значение 0 или 1.
Работа демультиплексора описывается уравнениями:
![]()

![]()
Функциональная схема демультиплексора, построенного по этим уравнениям для n=4, m=2 (рис.5.5).
|
|
Рис 5.5 Функциональная схема демультиплексора с четырьмя выходами.
5.4 Дешифраторы
Полным дешифратором называют комбинационную схему, имеющую n входов и 2n выходов и реализующую на каждом выходе функцию, представляющую собой минтерм n переменных.
Дешифраторы являются преобразователями кодов, выполняющих преобразование двоичного и двоично-десятичного кодов в унитарный код. Унитарный код двоичного n-разрядного числа представляется 2n разрядами, только один из разрядов которого равен 1 [6].
Поэтому в полном дешифраторе каждой комбинации значений входных сигналов х1,..., хn соответствует сигнал, равный 1, только на одном выходе, на остальных выходах сохраняются сигналы 0. На выходах вырабатываются 1 при минтермах соответственно:
![]()
![]()

Такой системе уравнений, например, для n=2 соответствует табл.5.7.
Таблица 5.7. Таблица истинности
|
х2 |
х1 |
f0 |
f1 |
f2 |
f3 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
Пример 5.2. Синтезировать преобразователь кода прямого замещения в двоично-десятичный код 2421.
Решение 1. Код прямого замещения представляет собой обычное представление одноразрядного десятичного числа в двоичной системе счисления, т.е.
![]()
2. Двоично-десятичный код 2421 соответствует представлению числа в виде
![]()
Таким образом, преобразователь кодов представляет собой схему с четырьмя входами и четырьмя выходами.
3. Составляют таблицу истинности для логической функции преобразователя кодов (табл.5.8).
Таблица 5.8
Таблица истинности преобразователя кодов
|
Десятичное число |
Код прямого замещения | Двоично-десятичный код 2421 на выходе | ||||||
|
х1 |
х2 |
х3 |
х4 |
у1 |
у2 |
у3 |
у4 |
|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| 4 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 |
| 6 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 |
| 8 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 9 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 |
ФУНКЦИЯ НЕ ОПРЕДЕЛЕНА |
||||
| 1 | 0 | 1 | 1 | |||||
| 1 | 1 | 0 | 0 | |||||
| 1 | 1 | 0 | 1 | |||||
| 1 | 1 | 1 | 0 | |||||
| 1 | 1 | 1 | 1 |
4. Получают логическую функцию преобразователя кодов в виде СДНФ путем записи "по единицам", представленную системой уравнений:
![]()
![]()
![]()
![]()
5. Получают логическую функцию в виде МДНФ с помощью карт Карно рис.5.6
|
х1х2 х3х4 |
00 | 01 | 11 | 10 |
х1х2 х3х4 |
00 | 01 | 11 | 10 | |
| 00 |
|
1 | 00 |
|
|
1 | ||||
| 01 |
|
х | 1 | 01 | х | 1 | ||||
|
|
|
х | х | 11 |
|
х | х | |||
| 10 | 1 | х | х | 10 |
|
х | х |
у1=х1+х2х3+х2х4
![]()
|
х1х2 х3х4 |
00 | 01 | 11 | 10 |
х1х2 х3х4 |
00 | 01 | 11 | 10 | |
| 00 |
|
1 | 00 | х | ||||||
| 01 |
|
х | 1 | 01 |
|
1 | х | 1 | ||
|
|
1 | х |
|
11 | 1 | 1 | х | х | ||
| 10 | 1 | х | Х | 10 | х | х |
Рис. 5.6. Карты Карно.
![]()
у4=х4
Синтезируемая схема реализует четыре функции. Ее можно представить как простое объединение схем, реализующих каждую функцию отдельно. Но это не экономично. Целесообразно преобразовать совокупность этих функций к такому виду, чтобы реализующие их схемы содержали общие части, а схема с четырьмя выходами представляла собой единое целое.
Для выполнения этого условия, используя избыточные наборы входных переменных х1х2х3х4, которые отмечены на картах Карно крестиками, образуют минимальные покрытия для каждой из четырех функций, которые включали бы возможно больше однотипных объединений клеток на картах.
В итоге получают МНДФ логической функции:
у1=х1+х2х3+х2х4=х1+х2(х3+х4)
![]()
![]()
у4=х4
5. Функциональная схема устройства на рис.5.7.
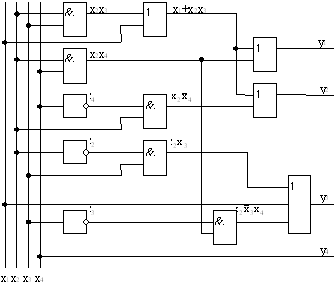
Рис. 5.7 Функциональная схема преобразователя кода прямого замещения в двоично-десятичный код 2421.
Пример 5.3. Синтезировать дешифратор для преобразования
двоично-десятичного кода в код, предназначенный для управления десятичным
индикатором (дешифратор 4![]() 10).
10).
Решение. 1. Двоично-десятичный код 2421 соответствует представлению числа в виде:
![]() .
.
Поэтому дешифратор должен иметь четыре входа.
2. Для управления десятичным индикатором на выходе необходимо получить десятичное число, т.е. дешифратор должен иметь десять выходов.
Таким образом дешифратор представляет собой схему с четырьмя входами и десятью выходами. Составляют таблицу истинности для логической функции дешифратора (табл.5.9)
Таблица 5.9
Таблица истинности дешифратора
|
Десятичное число |
Двоично-десятичный код на входе |
код на выходе | ||||||||||||
|
х1 |
х2 |
х3 |
х4 |
у0 |
у1 |
у2 |
у3 |
у4 |
у5 |
у6 |
у7 |
у8 |
у9 |
|
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 3 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 5 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 6 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| 7 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 8 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 9 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
ФУНККЦИЯ НЕ ОПРЕДЕЛЕНА |
||||||||||
| 1 | 0 | 1 | 1 | |||||||||||
| 1 | 1 | 0 | 0 | |||||||||||
| 1 | 1 | 0 | 1 | |||||||||||
| 1 | 1 | 1 | 0 | |||||||||||
| 1 | 1 | 1 | 1 |
4. Получают логическую функцию дешифратора в виде СДНФ путем записи " по единицам":
|
|
|
5. При синтезе функциональной схемы следует учитывать, отдельные функции содержат общие части, поэтому схему с десятью выходами представляют как единое целое (рис.5.8)

Рис. 5.8
Функциональная схема дешифратора для преобразования двоично-десятичного кода в
код, предназначенный для управления десятичными индикаторами (дешифратор 4![]() 10)
10)
5.5 Шифраторы
Шифраторы выполняют функцию, обратную дешифраторам, т.е. преобразуют унитарный код в двоичный или двоично-десятичный.
Пример 5.4. Синтезировать шифратор на пять входов, выход которого представляется в двоичном коде.
Решение. 1. Шифратор преобразует унитарный код в двоичный или двоично-десятичный.
Унитарный код двоичного n-разрядного числа представляется 2n разрядами, только один из которых равен 1.
Шифратор имеет пять входов. Число 5 в двоичном коде представляется тремя разрядами: 101, т.е. шифратор должен иметь три выхода.
В соответствии с этим составляют табл.5.10
Таблица 5.10
Таблица истинности
|
х1 |
х2 |
х3 |
х4 |
х5 |
у1 |
у2 |
у3 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 1 | ||||
| 1 | 0 | 1 | 0 | ||||
| 1 | 0 | 1 | 1 | ||||
| 1 | 1 | 0 | 0 | ||||
| 1 | 1 | 0 | 1 |
2. Получают логическую функцию шифратора в виде СДНФ путем записи "по единицам"
![]()
![]()
![]()
3. Функциональная схема шифратора в логическом базисе И-НЕ (рис.5.9.а) и в логическом базисе И, ИЛИ, НЕ (рис.5.9.б).
а). 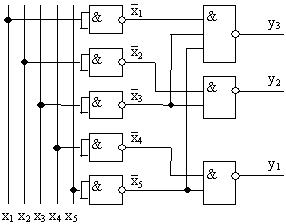
б) 
Рис. 5.9 Функциональная схема шифратора в логическом базисе И-НЕ (а) и в логическом базисе И, ИЛИ, НЕ (б)
5.6 Преобразователи кодов
Преобразователи кодов используют для шифрации и дешифрации цифровой информации и имеют n входов и m выходов. Соотношения между числами n и m могут быть любыми: n<>m.
5.7 Сумматоры
Сумматоры - это комбинационные устройства, осуществляющие суммирование чисел в двоичном коде.
Правила суммирования в простейшем случае - суммирования двух одноразрядных чисел, задаются таблицей двоичного сложения:
0+0=0
0+1=1
1+0=1
1+1=0+единица переноса в старший разряд.
Логическую функцию одноразрядного суммирования составляют на основании правил суммирования (табл. 5.11)
Таблица 5.11
Таблица истинности сумматора
Слагаемые |
Результат суммирования | ||
|
х1 |
х2 |
Si |
Цифра переноса в старший разряд, рi+1 |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Для получения логической функции одноразрядного суммирования в форме СДНФ производят запись " по единицам":
![]() ,
,
![]() ,
,
т.е. она реализуется двумя логическими функциями, а устройство имеет два выхода: Si и рi+1.
Схему, реализующую две функции, можно представить как простое объединение схем, реализующих каждую функцию отдельно, рис. 5.9:

Рис. 5.9 Функциональная схема одноразрядного сумматора: полусумматора.
Устройство оказывается синтезированным из двух самостоятельных частей, реализующих:
1) функцию исключающее ИЛИ (сумма по модулю два);
2) функцию конъюнкции И.
Такое устройство называется полусумматором.
Полный одноразрядный сумматор должен иметь вход для цифры переноса из предыдущего разряда рi и число слагаемых в нем оказывается равным трем: х1, х2, рi (табл.5.12). Логическую функцию для полного одноразрядного сумматора представляют таблицей истинности, составленной на основании правил суммирования.
Таблица 5.12
Таблица истинности полного одноразрядного сумматора
| Слагаемые | Результат суммирования | |||
|
Цифра переноса из предыдущего Разряда рi |
Первое слагаемое x1 |
Второе Слагаемое x2 |
Сумма Si |
Цифра переноса в старший разряд, pi+1 |
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
Для получения логической функции в алгебраической форме в виде СДНФ производят запись по "единицам":
![]()
![]() ,
,
Далее производят минимизацию логических функций. Выражение для Si не поддается минимизации изложенными ранее методами. Единственная возможность - это использовать вынесение за скобки:
![]()
Для выражения рi+1 можно получить сокращенную дизъюнктивную нормальную формы применив все операции склеивания и поглащения:
1-4: ![]() (по рi)
(по рi)
2-4: ![]() (по х2)
(по х2)
3-4: ![]() (по х1)
(по х1)
Сокращенная дизъюнктивная форма логической функции:
![]()
Таким образом, полный сумматор оказывается устройством с двумя выходами и реализуется двумя логическими функциями Si и Pi+1 с тремя аргументами x1, x2, P i.
Схему, реализующую несколько функций, можно представить как простое объединение схем, реализующих каждую функцию отдельно.
Функциональная схема в логическом базисе И, ИЛИ, НЕ на рис.5.10.


Рис.5.10 Функциональная схема полного одноразрядного сумматора.
Но такой путь, как правило, является неэкономичным. Схема оказалась реализованной на 16 базовых логических элементах.
Часто бывает целесообразно преобразовать совокупность данных логических функций к такому виду, чтобы реализующие их схемы содержали общие части, а схема с многими выходами представляла собой единое целое.
Поэтому продолжим преобразования.
На следующем этапе
преобразований целесообразно более простую реализацию функции ![]() использовать в качестве
составной части другой функции
использовать в качестве
составной части другой функции ![]() . Для такой функции табл.5.13.
. Для такой функции табл.5.13.
Таблица 5.13
Таблица истинности полного одноразрядного сумматора
|
|
|
|
|
|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | ´ |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | ´ |
| 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | ´ |
| 0 | 1 | 1 | 0 | ´ |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | ´ |
| 1 | 0 | 1 | 0 | ´ |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | ´ |
| 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | ´ |
| 1 | 1 | 1 | 1 | 1 |
Но таблица истинности для
![]() теперь
содержит избыточные наборы переменных, которые отмечены крестиками ´, т.е. функция оказывается частично
(не полностью) определенной. Используем для минимизации частично определенной
функции
теперь
содержит избыточные наборы переменных, которые отмечены крестиками ´, т.е. функция оказывается частично
(не полностью) определенной. Используем для минимизации частично определенной
функции ![]() карту
Карно (рис.5.11).
карту
Карно (рис.5.11).
|
|
00 | 01 | 11 | 10 |
| 00 |
|
|
1 | |
| 01 | ´ | ´ | ´ | |
| 11 | ´ |
|
||
| 10 |
|
|
|
´ |
Рис.5.11 Карта Карно.
Минимальному покрытию соответствует логическая функция:
![]()
После вынесения за скобки
![]() получают
подготовленную для реализации логическую функцию:
получают
подготовленную для реализации логическую функцию:
![]()
Функциональная схема для этой логической функции в логическом базисе И, ИЛИ, НЕ показана на рис. 5.12.
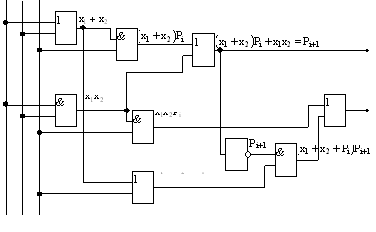
Рис.5.12 Минимизированная функциональная схема полного одноразрядного сумматора.
Схема оказалась реализованной на 9 базовых логических элементах, что почти в два раза меньше, чем в первой схеме. Это подтверждает целесообразность проведенных преобразований.
Для реализации схемы в базисах И-НЕ и ИЛИ-НЕ следует для логической функции применить формулу Де Моргана.
Получены схемы полных одноразрядных сумматоров.
Полные многоразрядные двоичные сумматоры составляются из одноразрядных.
Способов выполнения сложения многоразрядных чисел два: параллельный и последовательный.
Процедуру сложения двух
n-разрядных двоичных чисел ![]() можно представить рис.5.13.
можно представить рис.5.13.

Рис.5.13 Процедура сложения двух n-разрядных двоичных чисел
В младшем разряде
сумматора используется полусумматор (два входа для ![]() и
и ![]() ).
).
Начиная со второго
разряда необходимо иметь три входа: два для слагаемых ![]() и
и ![]() и один для сигнала переноса
и один для сигнала переноса ![]() с предыдущего
разряда, т.е. необходимо применять полный сумматор.
с предыдущего
разряда, т.е. необходимо применять полный сумматор.
Введем обозначения:
1) полного сумматора рис.5.14
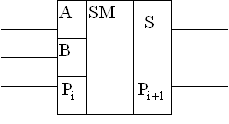
Рис.5.14 Обозначение на схеме полного сумматора
где S-выход суммы;
![]() - выход переноса;
- выход переноса;
![]() - вход переноса;
- вход переноса;
B - входы слагаемых цифр.
2) Полусумматора рис.5.15

Рис.5.15 Обозначение на схеме полу сумматора
В соответствии с рассмотренной схемой суммирования двух n-разрядных чисел схема n-разрядного сумматора может быть представлена в виде параллельного n-разрядного сумматора с последовательным переносом рис.5.16
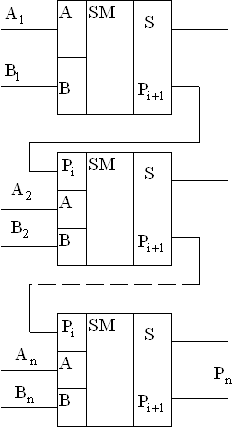
Рис.5.16 Параллельный n-разрядный сумматор
Число сумматоров здесь
равно числу разрядов. Выход переноса ![]() каждого сумматора соединен с
входом переноса
каждого сумматора соединен с
входом переноса ![]() следующего, более старшего разряда.
Слагаемые
следующего, более старшего разряда.
Слагаемые ![]() и
и
![]() складываются
во всех разрядах одновременно, а перенос
складываются
во всех разрядах одновременно, а перенос ![]() поступает с окончанием операции
сложения в предыдущем разряде.
поступает с окончанием операции
сложения в предыдущем разряде.
Быстродействие параллельного многоразрядного сумматора с последовательным переносом ограниченно задержкой переноса, так как формирование сигнала переноса на выходе старшего разряда не может произойти до тех пор, пока сигнал переноса младшего разряда не распространится последовательно по всей системе [7].
Это устройство нетрудно
сделать любой длины, однако суммирование будет закончено лишь тогда, когда
истечет время распространения сигналов переноса ![]() через всю цепь одноразрядных
сумматоров. Такой перенос иногда называют пульсирующим. При наиболее
неблагоприятных условиях для распространения переноса при сложении чисел
11...11 и 00... 001, произойдет “пробег” 1 переноса через весь сумматор от
самого младшего разряда к самому старшему. Поэтому в худшем случае время
распространения переноса
через всю цепь одноразрядных
сумматоров. Такой перенос иногда называют пульсирующим. При наиболее
неблагоприятных условиях для распространения переноса при сложении чисел
11...11 и 00... 001, произойдет “пробег” 1 переноса через весь сумматор от
самого младшего разряда к самому старшему. Поэтому в худшем случае время
распространения переноса ![]() где
где![]() - время распространения переноса в
одном разряде; n- число разрядов сумматора.
- время распространения переноса в
одном разряде; n- число разрядов сумматора.
При последовательном суммировании используется один, общий для всех разрядов полный (рис.5.17).
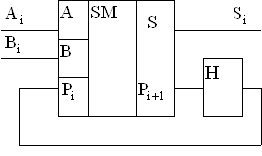
Рис.5.17 Сумматор с дополнительной цепью задержки
Оба слагаемых кодируются
последовательностями импульсов, которые синхронно вводятся в сумматор через
входы A и B, начиная с младших разрядов. Цепь задержки обеспечивает хранение
импульса переноса ![]() на время одного такта, т.е. до
прихода пары слагаемых следующего разряда, с которыми он будет просуммирован.
Задержку обеспечивает D-триггер. Для хранения и ввода слагаемых A и B, а
также для преобразования последовательного кода выходных импульсов
на время одного такта, т.е. до
прихода пары слагаемых следующего разряда, с которыми он будет просуммирован.
Задержку обеспечивает D-триггер. Для хранения и ввода слагаемых A и B, а
также для преобразования последовательного кода выходных импульсов ![]() в параллельный
применяют регистры сдвига. Работа регистров сдвига и триггера задержки
синхронизируется общим генератором тактовых импульсов.
в параллельный
применяют регистры сдвига. Работа регистров сдвига и триггера задержки
синхронизируется общим генератором тактовых импульсов.
Последовательные многоразрядные сумматоры имеют сравнительно невысокое быстродействие, так как одновременно суммируется лишь пара слагаемых. При этом они состоят из трех регистров, одноразрядного сумматора, триггера задержки (D-триггера) и генератора тактовых импульсов.
Быстродействие параллельного многоразрядного сумматора можно увеличить, заменив последовательный перенос на параллельный перенос с помощью специального узла: схемы ускоренного переноса СУП.
Принцип ускоренного (сквозного, параллельного) переноса заключается в том, что для каждого двоичного разряда дополнительно формируют два сигнала:
1) образования переноса ![]()
2) распространения переноса ![]()
В случае ![]() , т.е.
, т.е. ![]() в данном i-ом разряде
формируется сигнал переноса
в данном i-ом разряде
формируется сигнал переноса ![]() в следующий высший разряд
независимо от формирования функций суммы в предыдущих разрядах.
в следующий высший разряд
независимо от формирования функций суммы в предыдущих разрядах.
Если хотя бы одно из
слагаемых ![]() или
или
![]() равно 1
(т.е.
равно 1
(т.е. ![]() ),
то перенос в последующий разряд произойдет при наличии сигнала переноса из предыдущего
разряда.
),
то перенос в последующий разряд произойдет при наличии сигнала переноса из предыдущего
разряда.
Если функции
распространения переноса в двух соседних разрядах равны 1, т.е. ![]() , и при этом существует
сигнал переноса
, и при этом существует
сигнал переноса ![]() из предыдущего разряда, то
перенос производится непосредственно в разряд номер i+2.
из предыдущего разряда, то
перенос производится непосредственно в разряд номер i+2.
Процесс формирования ускоренного переноса описывается следующим уравнением:
![]() .
.
Пример 5.5. Синтезировать узел, осуществляющий суммирование двух одноразрядных двоичных чисел (полусумматор), на элементах И, ИЛИ, НЕ, на элементах И-НЕ и на элементах ИЛИ-НЕ.
Решение. 1. Составляют таблицу истинности для логической функции одноразрядного суммирования на основании правил суммирования одноразрядных чисел (5.14).
Таблица 5.14
Таблица истинности
| Слагаемые | Результат суммирования | ||
|
|
|
Сумма |
цифра переноса в старший разряд |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
2. Представляют логическую функцию в форме СДНФ путем записи “по единицам”:
![]() ;
;
![]()
3. Синтезируют полусумматор на элементах И, ИЛИ, НЕ (рис.5.18).
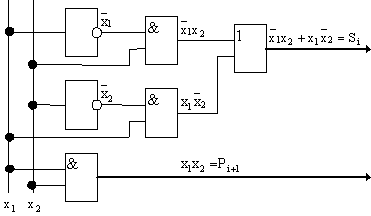
Рис.5.18 Полусумматор на элементах И, ИЛИ, НЕ
4. Для синтеза схемы на
элементах И-НЕ используют основное соотношение булевой алгебры: ![]() , поэтому
, поэтому
![]() .
.
Применяют закон Де Моргана:
![]() .
.
Равенство не изменится,
если к сомножителю ![]() прибавить
прибавить ![]() , а к сомножителю
, а к сомножителю ![]() -
- ![]() , т.к.
, т.к. ![]() ,
, ![]() :
:
![]() ,
,
![]() .
.
Вновь применяют закон Де Моргана:
![]() ,
,
![]() .
.
Полученные соотношения подставляют в исходное выражение:
![]() .
.
5. Функциональная схема сумматора на элементах И-НЕ (рис. 5.19).
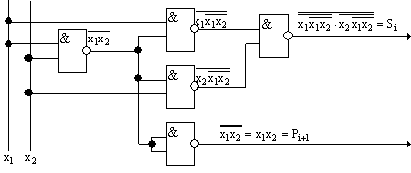
Рис. 5.19 Сумматор на элементах И-НЕ
6. Для синтеза схемы на элементах ИЛИ-НЕ представляют логическую функцию в форме СКНФ путем записи “по нулям”:
![]()
7. Проводят преобразование
![]()
8. Функциональная схема полусумматора на элементах ИЛИ-НЕ (рис.5.20).

Рис.5.20 Полусумматор на элементах ИЛИ-НЕ
Схемы на элементах ИЛИ-НЕ и И-НЕ оказалась проще - содержит 5 логических элементов, а на элементах И, ИЛИ, НЕ - 6.
Пример 5.6. Составить схему полного сумматора, используя полусумматоры.
Решение 1. Полный сумматор осуществляет
сложение трех цифр: двух цифр ![]() и
и ![]() , принадлежащих одному разряду
складываемых чисел, а также цифры переноса из предыдущего разряда
, принадлежащих одному разряду
складываемых чисел, а также цифры переноса из предыдущего разряда ![]() . В результате
суммирования этих трех цифр получается сумма
. В результате
суммирования этих трех цифр получается сумма ![]() и цифра переноса в старший разряд
и цифра переноса в старший разряд
![]() . Таким
образом, это устройство с тремя входами и двумя выходами.
. Таким
образом, это устройство с тремя входами и двумя выходами.
Полусумматоры имеют два
входа для ![]() и
и
![]() , и два
выхода для
, и два
выхода для ![]() и
и
![]() .
.
В соответствии с сочетательным законом:
![]()
т.е. можно сначала
сложить две цифры ![]() и
и![]() , а затем к промежуточной сумме
, а затем к промежуточной сумме ![]() прибавить
прибавить ![]() .
.
Поэтому полный сумматор можно представить как объединение двух полусумматоров.
Первый полусумматор
служит для сложения двух цифр ![]() и
и ![]() и обеспечивает выход
промежуточной суммы
и обеспечивает выход
промежуточной суммы ![]() и переноса
и переноса ![]() .
.
Второй полусумматор
складывает промежуточную сумму ![]() с цифрой переноса из предыдущего
разряда
с цифрой переноса из предыдущего
разряда ![]() ,
формирует перенос
,
формирует перенос ![]() и сумму
и сумму ![]() . При этом
. При этом
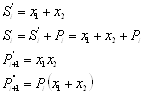
Из анализа таблицы
истинности для полусумматора следует, что при сложении трех цифр двумя
полусумматорами цифра переноса может образоваться только в одном полусумматоре:
![]() или
или ![]() . Поэтому для
получения
. Поэтому для
получения ![]() эти
переносы следует объединить логической ячейкой ИЛИ:
эти
переносы следует объединить логической ячейкой ИЛИ:
![]() .
.
Это выражение совпадает с полученным ранее для полного сумматора.
2. Функциональная схема полного сумматора, синтезированного из двух полусумматоров (рис. 5.21).
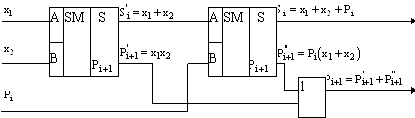
Рис.5.21 Полный сумматор, синтезированный из двух полусумматоров
5.8 Цифровые компараторы
Простой пример схемы сравнения (компаратора) одноразрядных двоичных чисел a и b рис.5.22

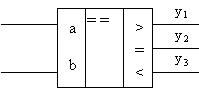
Рис.5.22 Функциональная схема и условное обозначение компаратора (логическая схема, выполняющая операцию “эквивалентность”, исключающее ИЛИ-НЕ).
Таблица 5.15
Таблица истинности компаратора
|
|
|
|
|
|
| A | b | a>b | a=b | a<b |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 |
Схема формирует высокий
потенциал на выходе ![]() при выполнении соответствующего
соотношения между числами a и b (табл. 5.15).
при выполнении соответствующего
соотношения между числами a и b (табл. 5.15).
Выпускаются ИМС для сравнения двух- и многоразрядных чисел [8].
Два n-разрядных двоичных
числа равны, когда попарно равны между собой все разряды этих чисел. Если,
например, числа a и b - четырехразрядные, то признаком их равенства будет: ![]() ;
; ![]() ;
; ![]() ;
; ![]() . Применяя
элемент уравнения для каждого разряда, факт равенства обоих чисел
. Применяя
элемент уравнения для каждого разряда, факт равенства обоих чисел ![]() установим в
случае
установим в
случае ![]() .
Если же
.
Если же ![]() ,
то
,
то ![]() .
.
Неравенство a>b обеспечивается в четырех случаях:
1) когда ![]() (
(![]() - старшие разряды чисел a, b)
- старшие разряды чисел a, b)
2) когда ![]() , но
, но ![]() ;
;
3) когда ![]() , но
, но ![]() , но
, но ![]() ;
;
4) когда ![]() , но
, но ![]() ,
, ![]() , но
, но ![]() ;
;
Очевидно, что для выполнения условия a<b достаточно поменять местами a и b.
5.9 Инкрементор
Инкрементор - это комбинационное устройство,
которое ко входному многоразрядному числу Q прибавляет в случае необходимости ![]() или 0, т.е. выполняют
операцию
или 0, т.е. выполняют
операцию ![]() .
.
Если Q=111...1 и ![]() , то
формируется сигнал
, то
формируется сигнал ![]() .
.
Схема инкрементора/декрементора, выполняющего операцию y=Q±C0, часто применяется в микропроцессорных системах для определения адреса следующей команды (рис. 5.23).

Рис.5.23 Схема инкрементора.
5.9 Коммутатор
Коммутатор - это комбинационно устройство с m
входами и n выходами, которые по заданным адресам ![]() входа, a
входа, a ![]() выхода соединяет между собой
требуемые вход и выход. Простейший коммутатор можно построить, включив последовательно
мультиплексор и демультиплексор.
выхода соединяет между собой
требуемые вход и выход. Простейший коммутатор можно построить, включив последовательно
мультиплексор и демультиплексор.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Пухальский Г. И. Логическое проектирование цифровых устройств радиотехнических систем.- Л.: Ленинградский университет, 1976.
2. Расчет элементов импульсных и цифровых систем радиотехнических устройств / Васильева В. П., Гришин Ю. П., Зюбенко В. Д. и др.; Под ред. Ю.М. Назаринова - М.: Высшая школа, 1976.
3. Петров В.П. Проектирование цифровых систем контроля и управления. - М.: Машиностроение, 1967.-460с.
4. Микропроцессоры и микропроцессорные компоненты интегральных микросхем: Справочник в 2 т. / Н.Н. Аверьянов, А.И. Березенко, Ю.И. Борщенко и др. ; Под ред. В.А. Шахнова.- М.: Радио и Связь, 1988.
5. Шило В.Л. Популярные цифровые микросхемы: Справочник.- Челябинск: Металлургия, Челябинское отделение, 1988-352с.
6. Зельдин Е.А. Цифровые интегральные микросхемы в информационно-измерительной аппаратуре.- Л.: Энергоатомиздат. Ленингр. отд-ние, 1986. - 280с.
7. Соломатин Н.М. Логические элементы ЭВМ.- М.: Высш. шк., 1987. - 144с.
8. Гольденберг Л.М., Малев В.А., Малько Г.Б. Цифровые устройства и микропроцессорные системы. Задачи и управления: Учеб. пособие для вузов. - М.: Радио и связь, 1992. - 226с.
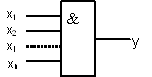
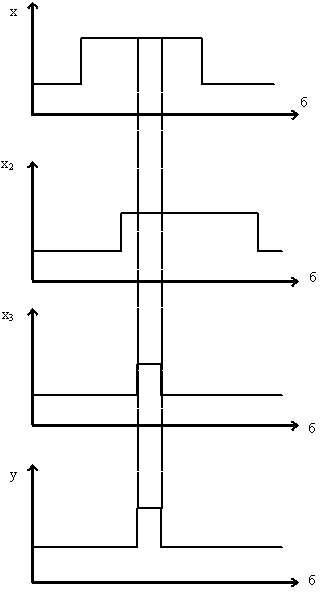

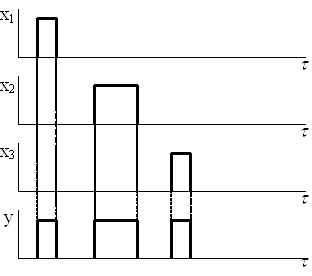

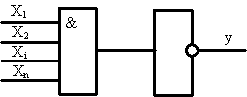




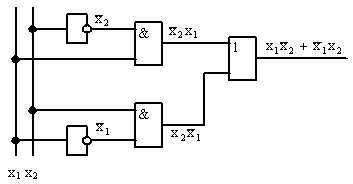

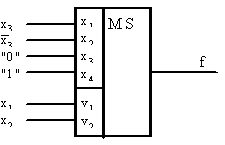
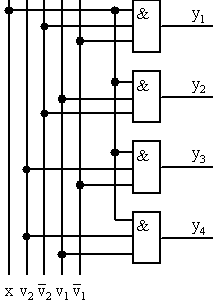
 х
х х
х х
х