Курсовая работа: Деление чисел в нормализованной форме
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Марийский государственный технический университет
Кафедра информатики и
системного программирования
Курсовая работа по дисциплине информатика на тему:
Деление чисел в нормализованной форме
Выполнила: студент ИВТ-11
Васильев Иван Федорович
Проверила: старший преподаватель
Кафедры ИиСП Иванова И.Н.
Йошкар-Ола
2009
Содержание
1. Теоретическая часть
1.1 Теория
1.2 Описание метода решения
2. Алгоритм (блок-схема) работы программы
2.1 Листинг программы
2.2 Тестирование программы
3. Вывод
Введение
Постановка задачи:
Ввод: два числа в десятичной СС в естественной форме. Программа переводит числа в нормализованную форму, делит нормализованные числа.
Вывод: частное от деления в нормализованной форме в десятичной СС.
В данной курсовой работе показан один из алгоритмов деления чисел в нормализованной форме. Такие программы удобны для быстрого получения нормализованного произведения чисел с помощью TP Pascal. Для реализации поставленной задачи я использовала теоретические сведения из курса информатики и ПнаЯВУ, а также полученные ранее знания в области программирования.
1. Теоретическая часть
1.1 Теория
Пусть имеются два числа X1 = M1·pk1
и X2 = M2·pk2 (здесь индексы у мантиссы
и порядка означают не систему счисления, а служат номерами чисел). Умножение
должно начинаться с выявления большего из k1 и k2,
нахождения модуля их разности 
k =|k1 - k2|
и сдвига вправо на k разрядов мантиссы того
числа, у которого k оказался меньше. Операция деления, проводимая как
над целыми, так и вещественными числами, приводит в общем случае к появлению
вещественного числа, поэтому целые числа предварительно преобразуются в
вещественный тип, т.е. переводятся в нормализованную форму. Очевидно, при
делении X1
X2 мантисса
частного M = M1/M2, а порядок k = k1-k2.
При этом непосредственно операция деления сводится к сдвигу делителя вправо и
последовательному вычитанию его из делителя (т.е. сложения с дополнительным
кодом вычитаемого). Как и в предыдущих операциях, результат деления при
необходимости нормализуется.
1.2 Описание метода решения
Метод решения заключается в считывании из INPUT в файл чисел, переписывании чисел без разделения их на целую и дробную части, подсчитывании количества разрядов чисел, выбора большего разряда, и сдвига вправо на k разрядов меньшего числа, затем деления нормализованных чисел, если возникает необходимость - нормализации результата, и вывода суммы в OUTPUT.
2. Алгоритм (блок-схема) работы программы
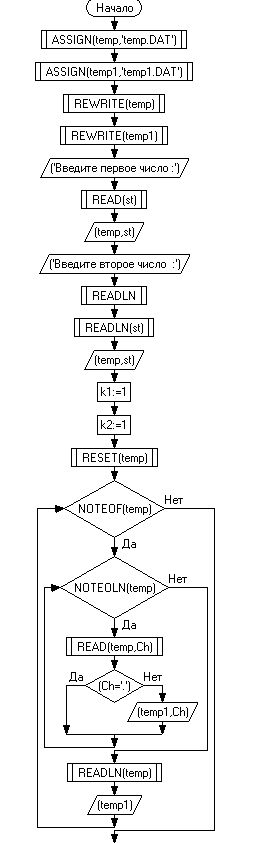
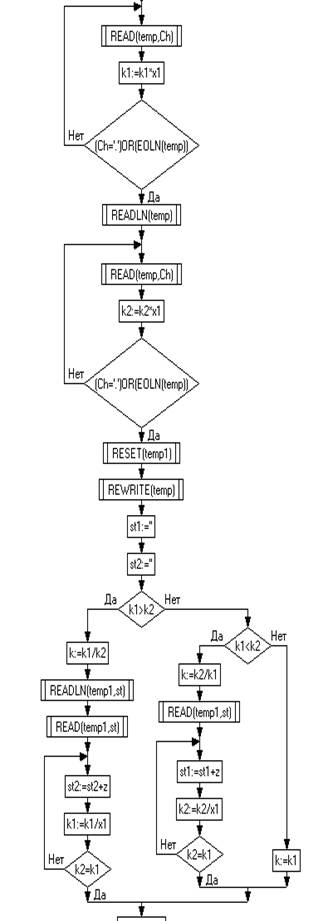
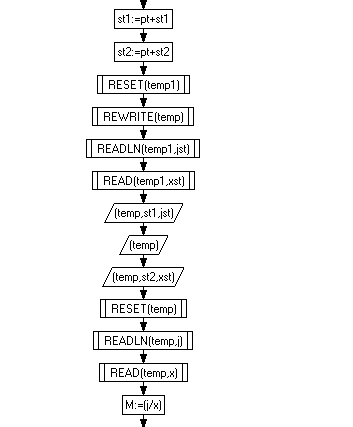
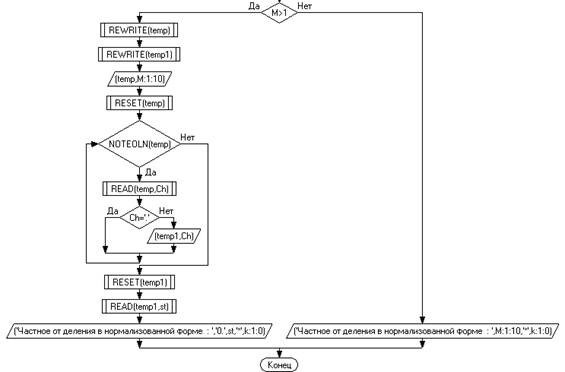
2.1 Листинг программы
Программа считывает числа в файл, убирает ‘. ’, считает количество разрядов - k умножаем на 10, до тех пор пока не дойдем до дробной части, с помощью IF THEN ELSE находим больший k у одного из чисел, а к меньшему числу добавляем нули, тем самым сдвигая его вправо, в то же время делим больший k на 1 разряд, предварительно присвоив его другому элементу, до тех пор пока k1 не будет равно k2, записываем в файл числа построчно, начиная с “0. ” - для нормализации, затем нули (если таковые имеются), и само число без “. ”. Считываем записанное построчно как числа и выполняем деление. Часто возникают ситуации, когда необходима нормализация результата, его нормализуем таким же образом как и вводимые числа. Выводим результат + “*k”.
PROGRAM DELENIEVNORMFORME;
USES CRT;
CONST
pt='0. ';
z='0';
x1=10;
VAR
lst1,lst2: INTEGER;
j,x,M,k1,k2,k: REAL;
st,st1,st2,jst,xst: string;
temp,temp1: text;
Ch: CHAR;
BEGIN
ASSIGN (temp, 'temp. DAT'); { Создаем временные файлы, для промежуточных преобразований над числами }
ASSIGN (temp1, 'temp1. DAT');
REWRITE (temp);
REWRITE (temp1);
WRITELN ('Введите первое число: '); {Считываем оба числа в файл}
READ (st);
WRITELN (temp,st);
WRITELN ('Введите второе число: ');
READLN;
READLN (st);
WRITE (temp,st);
k1: =1;
k2: =1;
RESET (temp);
WHILE NOT EOF (temp) {Переписываем числа во второй файл, убирая '. '}
DO
BEGIN
WHILE NOT EOLN (temp)
DO
BEGIN
READ (temp,Ch);
IF (Ch = '. ')
THEN
ELSE
WRITE (temp1,Ch);
END;
READLN (temp);
WRITELN (temp1)
END;
RESET (temp);
REPEAT {Считаем количество разрядов первого числа}
BEGIN
READ (temp,Ch);
k1: =k1*x1;
END
UNTIL (Ch = '. ') OR (EOLN (temp));
READLN (temp);
REPEAT {Считаем количество разрядов второго числа}
BEGIN
READ (temp,Ch);
k2: =k2*x1;
END
UNTIL (Ch = '. ') OR (EOLN (temp));
RESET (temp1);
REWRITE (temp);
st1: ='';
st2: ='';
IF k1>k2 {ищем на сколько разрядов сдвигать вправо меньшее число }
THEN
BEGIN
k: =k1/k2;
READLN (temp1,st);
READ (temp1,st);
REPEAT
BEGIN
st2: =st2 + z;
k1: =k1/x1;
END;
UNTIL k2=k1;
END
ELSE
IF k1<k2
THEN
BEGIN
k: =k2/k1;
READ (temp1,st);
REPEAT
BEGIN
st1: =st1 + z;
k2: =k2/x1;
END
UNTIL k2=k1;
END
ELSE
k: =k1;
st1: =pt+st1; {Нормализуем числа}
st2: =pt+st2;
RESET (temp1);
REWRITE (temp);
READLN (temp1,jst);
READ (temp1,xst);
WRITE (temp,st1,jst);
WRITELN (temp);
WRITE (temp,st2,xst);
RESET (temp);
READLN (temp,j);
READ (temp,x);
M: = (j/x); {делим}
IF M > 1 { при необходимости результат деления нормализуем }
THEN
BEGIN
REWRITE (temp);
REWRITE (temp1);
WRITE (temp,M: 1: 10);
RESET (temp);
WHILE NOT EOLN (temp)
DO
BEGIN
READ (temp,Ch);
IF Ch = '. '
THEN
ELSE
WRITE (temp1,Ch);
END;
RESET (temp1);
READ (temp1,st);
WRITE ('Частное от деления в нормализованной форме: ','0. ',st,'*',k: 1: 0);
END
ELSE
WRITE ('Частное от деления в нормализованной форме: ', M: 1: 10,'*',k: 1: 0);
END.
2.2 Тестирование программы
Для тестирования введем два числа
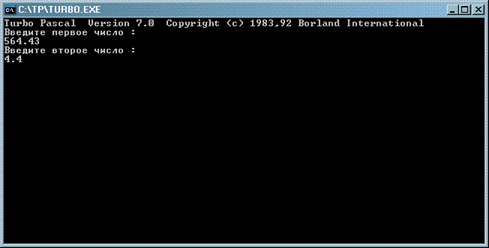
На выходе имеем частное от деления в нормализованной форме
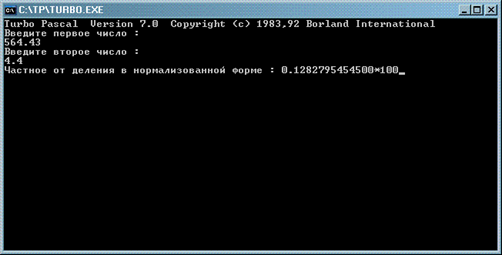
3. Вывод
При выполнении этой курсовой работы, был составлен наиболее оптимальный алгоритм деления чисел в нормализованной форме. Более глубоко изучена работа со строковыми данными и типами REAL и INTEGER. Эта программа в первую очередь наиболее необходима людям, которые вручную делят числа в нормализованной форме, чтобы заменить ручной труд на машинный.