Научная работа: Математическая модель процесса вытяжки трубчатой заготовки

Основная идея МКЭ основывается на замене некоторой непрерывной величины в пределах рассматриваемой области дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определённых на конечном числе подобластей, называемых конечными элементами (КЭ). Неизвестная искомая величина в пределах каждого КЭ аппроксимируется, как правило, полиномиальной функцией заданного вида с учётом требования непрерывности на границах смежных КЭ. При этом выбор формы конечного элемента и вида выражения, аппроксимирующего действительный закон изменения исследуемой величины в пределах КЭ, является одним из наиболее ответственных моментов в общей процедуре МКЭ, от которого существенно зависит точность приближённого решения. Таким образом, непрерывная в пределах исследуемой области неизвестная величина (например, перемещение, скорость перемещения, напряжение, температура и т. д.) представляется через конечное число её дискретных значений в узлах элементов.

Построение разрешающих уравнений МКЭ для решения задач механики деформируемых сред базируется на соответствующих вариационных принципах и вытекает из оптимизации некоторой интегральной величины (функционала), связанной с работой или мощностью напряжений и внешней приложённой нагрузки при соблюдении заданных граничных условий. В общем виде такой функционал с учётом действия массовых и поверхностных сил можно представить выражением:

,(1)

где A_Д - работа или мощность внутренних сил; A_М - работа или мощность, развиваемая массовыми силами; A_В - работа или мощность внешних сил.

Дальнейшая процедура МКЭ предусматривает представление выражения (2.1) в виде функционала значений, неизвестных только в узлах КЭ, и построение разрешающей системы уравнений путем минимизации J по всем узловым переменным:

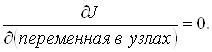(2)

Однако, указанный способ получения разрешающих уравнений для КЭ с помощью функционала (1) не является единственно возможным. В настоящее время уравнения для элементов получают путем минимизации функционала, связанного с рассматриваемым дифференциальным уравнением соответствующей задачи математической физики. Известны также конечно-элементные решения, основанные на методе Галеркина. В последнем случае отпадает необходимость в вариационной формулировке задачи.

Способ получения разрешающих уравнений для КЭ, основанный на оптимизации функционала (1), является общепризнанным при теоретическом решении задач ОМД, поскольку вариационные принципы имеют наглядный физический смысл и достаточно строгое математическое обоснование.

По отношению к функционалу (1) известны три вида вариационных принципов теории пластичности в зависимости от того, через какие переменные величины выражена мощность (потенциальная энергия) деформации.

Принцип минимума полной мощности (полной энергии) или принцип возможных изменений деформированного состояния рассматривает мощность (потенциальную энергию) деформируемого тела как функционал произвольной системы скоростей (перемещений), удовлетворяющей кинематическим граничным условиям, и который принимает минимальное значение для системы скоростей (перемещений), фактически реализуемой в деформируемом теле.

Принцип минимума дополнительной работы Кастильяно или принцип возможных изменений напряжённого состояния рассматривает дополнительную работу как функционал произвольной системы напряжений, удовлетворяющей уравнениям равновесия внутри тела и на его поверхности, и который принимает минимальное значение для системы напряжений, фактически реализуемой в деформируемом теле.

В вариационном принципе Рейсснера или принципе возможных изменений напряжённого и деформированного состояний мощность (энергия) рассматривается как функционал скоростей и напряжений, и переменные той и другой группы варьируются независимо друг от друга.

Каждому из перечисленных вариационных принципов соответствует определённая форма МКЭ. Принципу минимума полной мощности (полной энергии) соответствует кинематический метод, принципу минимума дополнительной работы - метод напряжений, а вариационному принципу Рейсснера - смешанный метод.

При нагружении тела потенциальная энергия внешних сил изменяется. При этом внешние силы совершают работу. Потенциал внешних сил Q на возможных перемещениях δu численно равен работе этих сил:

(3)

где P_i – поверхностные силы, S – площадь поверхности тела.

В результате изменения потенциальной энергии внешних сил тело деформируется и накапливает потенциальную энергию деформации W

(4)

где s_ij - компоненты тензора напряжения, e_ij - компоненты тензора деформации, V – объём тела.

Сумма энергии деформации и потенциала внешних сил равна полной потенциальной энергии:

(5)

В соответствии с принципом возможных перемещений Лагранжа изменение полной потенциальной энергии на возможных перемещениях равняется нулю:

(6)

При этом под возможными перемещениями du понимаются сколь угодно малые отклонения системы от положения равновесия, допускаемые наложёнными на систему связями. Из уравнения (6) следует, что в состоянии равновесия энергия П имеет стационарное значение. Можно показать, что в положении устойчивого равновесия этот экстремум соответствует минимуму.

С учётом изложённого вариационное уравнение Лагранжа для статической задачи имеет вид:

(7)

Минимизируя потенциальную энергию по возможным перемещениям, получаем систему линейных уравнений, решая которую определяем значения внешних сил.

2. Основные соотношения метода конечных элементов

Простейшим элементом, применяемым для решения осесимметричной задачи механики деформируемого твердого тела, является тороидальный элемент с тремя узлами, расположёнными в вершинах треугольного сечения (Рис. 1.).

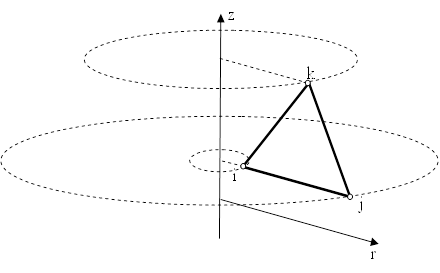
Рис. 1. Конечный элемент в задаче осесимметричной деформации

Вектор перемещений узловых точек конечного элемента в случае осесимметричной деформации имеет вид:

.(8)

Произвольная точка элемента получает перемещения u_r и u_z в направлении осей r и z. Поэтому матрица u имеет вид:

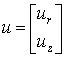.(9)

Узловые перемещения  и u связаны между собой матрицей аппроксимирующих функций N:

(9’)

Наиболее распространен способ получения приближённых решений на основе использования вариационного уравнения по методу Релея - Ритца. Он заключается в том, что функции перемещений задаются в виде интерполяционного полинома. Если ограничиться полиномом первой степени, то эти функции будут иметь вид:

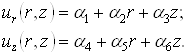(10)

Здесь a_i - произвольные постоянные. При линейной аппроксимации стороны треугольника после деформирования элемента остаются прямыми.

Выразим a_i через перемещения узлов элемента. В результате матрица N примет вид:

(11)

S - площадь сечения элемента:

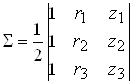,(12)

где r_i, z_i - координаты i-го узла в соответствующих осях.

Деформированное состояние в любой точке тела описывается тензором малых деформации Коши:

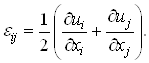(13)

В условиях осесимметричной задачи тензор деформации второго ранга сводится к вектору:

(14)

компоненты которого выражаются через производные перемещений по соответствующим координатам:

.(15)

Связь между составляющими векторов деформации и перемещений можно представить одним матричным равенством:

(16)

где B – матричный дифференциальный оператор:

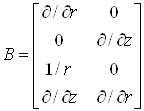.(17)

Используя (16) и (17), можно выразить деформации через узловые перемещения

.(18)

Матрица функций формы C для осесимметричной деформации:

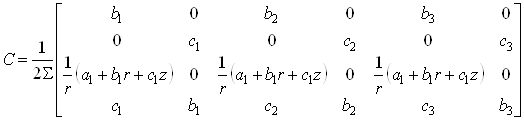.(19)

Коэффициенты матрицы C зависят от координат r и z точки внутри элемента. Для треугольника с узлами в вершинах координаты r и z можно заменить средними по элементу значениями:

(20)

Вектор напряжений s имеет вид:

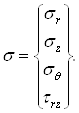(21)

Выразим с помощью линейного закона, выражаемого матрицей жёсткости, напряжения через узловые перемещения

,(21’)

где D – матрица материальных констант.

Потенциальная энергия деформации элемента с учётом (20) и (19)

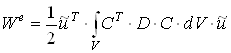.(22)

Интеграл в выражении (2.22) есть матрица жёсткости выбранного элемента

,(23)

Элементарный объём . Поэтому матрица жёсткости элемента записывается следующим образом:

,(24)

где S – площадь элемента.

С учётом проделанных преобразований уравнение равновесия элемента через узловые перемещения выражается в форме:

(25)

где K - матрица жёсткости; P,  - векторы внешних сил и узловых перемещений, соответственно.

При наличии упругих и пластических деформации связь между напряжениями и деформациями нелинейна. Решение нелинейной системы уравнений весьма трудоемко. Поэтому при использовании деформационной теории часто используют кусочно-линейный закон связи напряжений и деформации. Тогда при решении задачи в приращениях напряжений Ds и деформации De, связь между которыми можно считать линейной, получаем систему линейных уравнений:

(26)

Одним из способов решения задачи в приращениях является метод последовательных нагружений. Для квазистатической задачи приращения внешних сил DP вычисляются на шаге по времени Dt. При этом вектор внешних сил P в момент времени t равен:

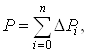(27)

где n – шаг нагружения.

Таким образом, с учётом вышеизложённого, вариационное уравнение равновесия в матричной записи принимает вид:

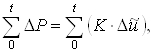(28)

где - вектор приращений перемещений.

3. Представление матрицы жёсткости

В пределах упругости связь между приращениями напряжений и деформации выражается законом Гука. Согласно ему компоненты приращений деформации являются линейными функциями приращений напряжений. Пластическое состояние материала описывается теорией малых упругопластических деформации Ильюшина. Принимается теория изотропного упрочнения. Объёмная деформация в пластической зоне остается упругой и для нее выполняется объёмный закон Гука:

,(29)

где q - относительное изменение объёма.

Модуль объёмного сжатия k для изотропного тела в случае осесимметричной деформации имеет вид:

.(30)

Модуль сдвига G связан с модулем Юнга E и коэффициентом Пуассона n формулой:

в упругой области:

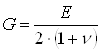(31)

в пластической:

(32)

Здесь H – касательный модуль упрочнения. Коэффициент Ляме - l определяется формулой:

(33)

Таким образом, матрица материальных констант D имеет вид:

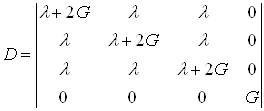.(34)

Следует особо отметить, что использовать матрицу жёсткости в таком виде для пластического состояния можно, только связывая приращения деформации и напряжений, о чем было сказано ранее при выводе уравнения равновесия.

Зная текущее состояние элемента, предел текучести, накопленную деформацию и приращения внешних сил, можно определить изменение напряжённо-деформированного состояния на шаге приращения перемещений Du и сил DР, используя для вычисления K по формуле ( упругое или пластическое представление матрицы жёсткости.

4. Пластическая деформация

Пластическая деформация твердого тела рассматривается в рамках деформационной теории пластичности. Приняты следующие исходные положения:

¾        тело изотропно;

¾        относительное изменение объёма мало и является упругой деформацией, пропорциональной среднему давлению: или ;

¾        полные приращения составляющих деформации De_ij складываются из приращений составляющих упругой деформации De_eij и пластической деформации De_pij:

;

¾        девиаторы приращений напряжения и деформации пропорциональны: .

Напряжённо-деформированное состояние элемента на i+1 шаге характеризуется интенсивностью деформации e_i:

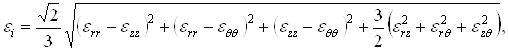(35)

где e_ij - компоненты тензора деформации.

Если интенсивность деформации какого - либо конечного элемента превысила текущий предел упругости по деформациям , то этот элемент переходит из упругого в пластическое состояние. Если материал упрочняется при пластическом деформировании, то соответствующая пределу упругости деформация ε_е увеличивается на величину De_е (Рис. 7):

(36)

Вычисление предела упругости по деформациям , достигнутого на шаге k определяется суммированием:

.(37)

Имеется в виду, что в упругой области предел упругости не изменяется, его приращения не вычисляются и равны нулю.

Накопленная пластическая деформация определяется разностью интенсивностей полной деформации e_i и деформации e_e, соответствующей пределу упругости:

(38)

Излагаемые в дальнейшем итерационные методы для достижения удовлетворительной сходимости требуют соблюдения непрерывности и гладкости кривой упрочнения. Поэтому в конце упругого участка кривой упрочнения введён нелинейно упругий участок, на котором модуль упрочнения вычисляется по формуле:

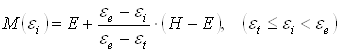,(39)

где  - интенсивность деформации, соответствующая пределу пропорциональности.

Соотношение (39) выражает пропорциональное изменение модуля упрочнения при переходе от упругого состояния к пластическому. Предел упругости по напряжениям в этом случае будет определяться соотношением

,(40)

где e_еp – деформация в области нелинейной упругости:

.

Вектор приращений компонент тензора напряжения на шаге k в пластическом состоянии определяется по приращениям компонент деформации:

.(41)

Вектор компонент напряжения на шаге k в упругом и пластическом состоянии суммируется по приращениям:

.(42)

Интенсивность напряжений определяется по компонентам тензора напряжения s_ij:

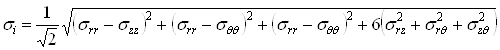.(43)

Рис. 2. Изменение предела упругости по деформациям при упрочнении

Если интенсивность деформации уменьшилась:

,(44)

то материал разгружается и переходит в упругое состояние. При нарушении неравенства (2.44) вновь происходит переход элемента в пластическое состояние.

5. Оценка повреждаемости заготовок

Для оценки деформируемости и прогнозирования разрушения заготовок в процессах обработки давлением получила развитие феноменологическая теория разрушения, использование которой основано на полученных опытным путем диаграммах пластичности и информации о напряжённо-деформированном состоянии в процессах обработки металлов давлением.

Оценку деформируемости заготовок, а также расчёт предельных технологических параметров проводят с помощью деформационных критериев, в основу которых положены ограничения, накладываемые на деформации. При этом для процессов, сопровождающихся монотонным, но сложным деформированием, в качестве меры повреждений принимают обычно некоторую скалярную характеристику.

Если влиянием истории деформирования пренебречь, то можно использовать критерий Смирнова-Аляева:

(45)

Либо, нормируя на единицу, получим меру повреждений y:

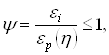(46)

где e_p(h) - предельная деформация в момент появления первых трещин, обнаруживаемых визуально; h - показатель напряжённого состояния:

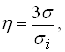(47)

s - среднее нормальное напряжение; s_i – интенсивность напряжений.

Для учёта влияния истории деформирования и использования соотношения (47) для простого нагружения, примем за меру повреждений y выражение (критерий Колмогорова):

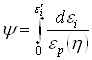,(48)

где  - степень деформации к рассматриваемому моменту; - предельная деформация, определяемая по диаграммам пластичности соответствующих материалов.

Добавление в конечно-элементную модель критерия деформируемости позволило проводить контроль на разрушение заготовки во время деформирования, а также прогнозировать состояние готового изделия.

6. Взаимодействие заготовки с инструментом

Заготовка представляет собой совокупность узлов, связанных между собой конечно-элементной сеткой. Далее “узлами” будут называться узлы конечно–элементной сетки заготовки. Поведение узлов описывается соотношениями МКЭ. Инструмент является абсолютно жёстким телом, ограниченным непроницаемыми для узлов заготовки границами. Границы инструмента аппроксимируются прямолинейными и радиусными участками, состыкованными друг с другом в единую поверхность. В дальнейшем под именем “граница” будет пониматься граница инструмента. Инструмент может быть неподвижным и подвижным. Для адекватного описания технологических процессов штамповочного производства математическая модель позволяет использовать один подвижный инструмент и несколько неподвижных (например, матрица и оправка).

Неподвижный инструмент зафиксирован в пространстве. В случае попадания узла заготовки на границу такого инструмента на его (узла) перемещения накладываются ограничения – граничные условия, такие, что узел может двигаться только вдоль границы или от неё. Математически эта модель реализуется следующим образом.

В точке касания узла границы вычисляется угол наклона границы. В осесимметричной задаче горизонталь параллельна радиальной оси, а вертикаль – оси симметрии тела. Если граница в этой точке параллельна осевому направлению, то узлу запрещаются радиальные перемещения. Если же граница параллельна радиальному направлению, то узлу запрещаются осевые перемещения. В случае с наклонной границей устанавливается связь между радиальной и осевой степенями свободы узла:

,(49)

где r – радиальная степень свободы; z – осевая; k – тангенс угла наклона границы.

В матричном представлении это означает, что в матрицу жёсткости добавляется дополнительная строка с единицей на позиции, соответствующей номеру запрещённой степени свободы. Для наклонной границы используется соотношение:

(50)

То есть в ячейки, соответствующие степеням свободы r и z данного узла, вносятся стоящие при них в уравнении (50) коэффициенты. Таким образом, удовлетворяется уравнение связи (49).

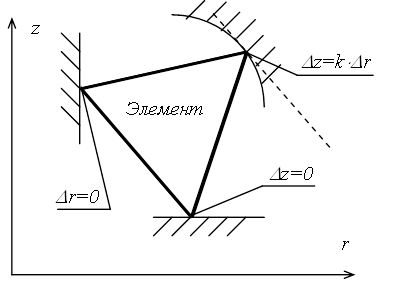
Рис. 3. Ограничения неподвижных границ

Подвижная граница перемещается в заданном направлении (вертикальном или горизонтальном, в зависимости от вида процесса) на величину DH на каждом шаге:

(51)

где H – полный ход инструмента; i – число шагов решения.

Если после очередного перемещения границы какой-либо узел (или несколько) может оказаться “в теле” инструмента, то ему назначается принудительное перемещение на величину Dh:

или(52)

Здесь R, Z – координаты подвижной границы; r, z – координаты узла.

Таким образом, перемещение узла в направлении перпендикулярной границе степени свободы будет обеспечивать его движение вместе с границей, включая момент касания. В этом случае перемещение узла перпендикулярно границе не запрещается, а подчиняется равенствам:

или(53)

Для системы уравнений это означает внесение в соответствующие данному узлу ячейки матрицы жёсткости коэффициентов 0 и 1 в зависимости от направления движения и в правую часть величины Dh.

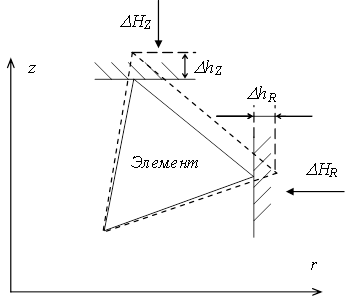
Рис. 4 Ограничения подвижных границ

Подвижная наклонная граница моделируется так же, как подвижная вертикальная или горизонтальная. Возникающая при этом ошибка, связанная со смещением узла вдоль границы минимизируется последовательными приближениями (см. Рис. 5).

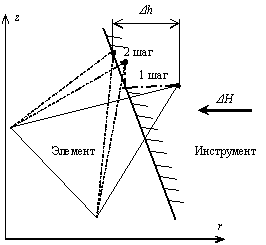
Рис. 5. Процедура уточнения положения узла при смещении его подвижным инструментом

7. Трение

При пластическом формоизменении на границе контакта материала и инструмента возникает сила трения. При этом направление течения материала зависит от величины силы трения, то есть направление силы трения на границе контакта заранее не известно и может изменяться.

Модуль напряжения трения определяется законом Кулона (54):

,(54)

где s_N – нормальное напряжение на границе инструмента; m – коэффициент трения скольжения; t_K – касательное к границе напряжение .

Рис. 6. Контакт конечного элемента заготовки с инструментом

При пластическом течении касательное напряжение в элементах t_K, контактирующих с внешними телами (матрица или пуансон), не должно превышать предел текучести при сдвиге t_S:

(55)

Для выполнения этого условия предложен следующий алгоритм расчёта. Для элемента, лежащего на границе, определяется касательное напряжение t_K, по которому вычисляется узловая сила трения:

(56)

где S_K – площадь контакта элемента с границей инструмента. Если к узлу примыкают два элемента, лежащие на границе, то узловая сила трения получается суммированием сил, вычисленных по формуле (56). Для определения направления силы трения реализуется следующий алгоритм. Сначала выполняется шаг нагружения без учёта трения (F_TP=0). Затем по результатам этого шага в каждом узле на границе контакта определяется нормальная узловая сила на границе контакта, приращение перемещения вдоль неё и, описанным выше способом, сила трения.

В процессе деформирования узлы, скользящие по границе инструмента, могут останавливаться и затем менять направление движения. В неподвижном состоянии узловая сила трения может оказаться меньше рассчитанной по формулам (54) – (56). Для этого введено последовательное уточнение силы F_TP прибавлением к ней величины невязки DF_TP:

(57)

Здесь n – номер итерации при уточнении силы трения.

Начальное значение невязки определяется силой трения:

(58)

Последующие значения невязки могут менять знак:

(59)

Эта формула обеспечивает рост силы трения в направлении противоположном движению. Если сила трения возрастает настолько, что меняет направление движения узла, то эта же формула обеспечит уменьшение силы трения.

Сходимость итерационного процесса обеспечивается уменьшением величины невязки при смене направления движения:

(60)

Кроме того, рост силы трения F_TP ограничен её предельным значением , вычисленным по формулам (54) – (56). Описанная итерационная процедура приближает силу трения к значениям, изображённым на графике (Рис. 7).

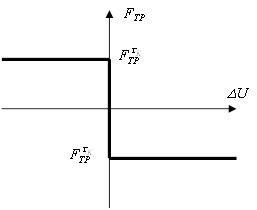
Рис. 7. Зависимость силы трения от направления движения узла

Основные выводы

1. Приведенная математическая модель, сделанная на базе метода конечных элементов, является наиболее универсальной и адекватной с точки зрения оценки протекающих в ней процессов.

2. Модель подвижной наклонной границы позволяет более точно представить процесс, а также оценить картину деформирования и течения материала на радиусах скругления инструментов.

3. Создание на начальном этапе решения задачи трех одинаковых копий матрицы жесткости и последующее в ходе выполнения наложение на две из них условий, связанных с перемещениями узлов, и использование третьей матрицы без изменения для определения узловых сил по перемещениям позволило сократить время вычислений, так как создание копии является более быстрым процессом, чем формирование матрицы жесткости.

4. Введение в модель учета повреждаемости заготовки позволило не только проводить контроль за разрушением заготовки непосредственно во время протекания процесса, но и прогнозировать состояние изделия, полученного смоделированным методом.