Курсовая работа: Основы расчёта оболочек
Омский государственный технический университет
Кафедра “Авиа- и ракетостроение”
Специальность 160801 - “Ракетостроение”
Курсовая работа
по дисциплине
“Строительная механика летательных аппаратов”
Основы расчёта оболочек
Омск 2005
Содержание
1. Расчет цилиндрической оболочки, подкрепленной шпангоутами
2. Исследование напряжённо-деформированного состояния полусферической оболочки, заполненной жидкостью
3. Исследование напряжённо-деформированного состояния сферической оболочки, заполненной жидкостью
4. Расчёт сферического топливного бака с опорой по экватору
5. Расчёт бака на прочность
Список литературы
1. РАСЧЕТ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ, ПОДКРЕПЛЕННОЙ ШПАНГОУТАМИ
Условие задачи. Рассмотрим цилиндрическую оболочку
постоянной толщины ![]() , радиуса
, радиуса ![]() , подкрепленную
шпангоутами, равномерно расположенными по её длине. Сечение шпангоута:
, подкрепленную
шпангоутами, равномерно расположенными по её длине. Сечение шпангоута: ![]() . Оболочка нагружена
избыточным давлением
. Оболочка нагружена
избыточным давлением ![]()
![]() (рис.1).
(рис.1).
Цель расчета. Определить минимальное расстояние
между шпангоутами ![]() , которое
позволяет исключить взаимное влияние на оболочку двух соседних шпангоутов.
, которое
позволяет исключить взаимное влияние на оболочку двух соседних шпангоутов.
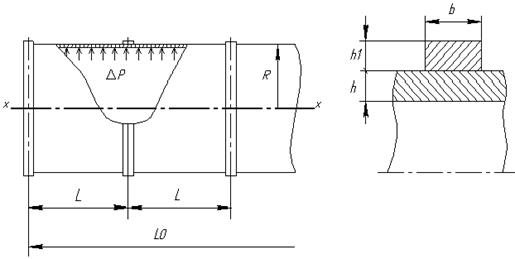
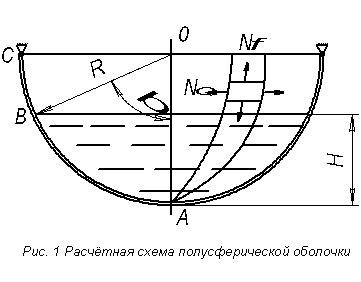
Рис.1. Расчетная схема
Исходные данные
Погонная нагрузка ![]() МПа;
МПа;
Радиус оболочки ![]() м;
м;
Толщина оболочки ![]() м;
м;
Ширина шпангоута ![]() , м;
, м;
Толщина шпангоута ![]() , м;
, м;
Материал оболочки:
марка ВТ6С (О);
коэффициент Пуассона ![]() ;
;
модуль Юнга ![]()
Выполнение расчёта
Расчётная схема 1. Шпангоуты абсолютно жёсткие
Определим цилиндрическую
жёсткость оболочки ![]() по формуле:
по формуле:
![]() ;
;
![]()
Вычислим коэффициент
затухания ![]() гармонической функции
гармонической функции ![]() по формуле:
по формуле:
![]() ;
;
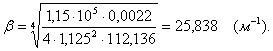
Определим силу
взаимодействия ![]() между
шпангоутами и оболочкой:
между
шпангоутами и оболочкой:
![]()
![]()
Определим перерезывающую
силу ![]() на краю оболочки:
на краю оболочки:
![]()
![]()
Определим погонный
изгибающий момент ![]() в месте
установки шпангоута:
в месте
установки шпангоута:
![]()
![]()
![]()
Погонный изгибающий
момент ![]() по длине оболочки,
затухающий по периодическому закону, вычислим по следующей формуле:
по длине оболочки,
затухающий по периодическому закону, вычислим по следующей формуле:
![]()
![]()
где ![]() - число расчётных точек на
всей области существования функции
- число расчётных точек на
всей области существования функции ![]() .
.
Принимаем ![]() .
.
Так как область
существования гармонической функции ![]() определяется
условием
определяется
условием ![]() , то находим шаг вычислений
, то находим шаг вычислений
![]() момента
момента ![]() из выражения:
из выражения:
![]() ;
;
![]()
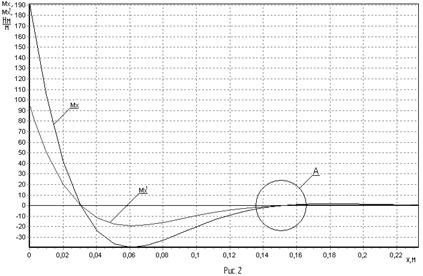
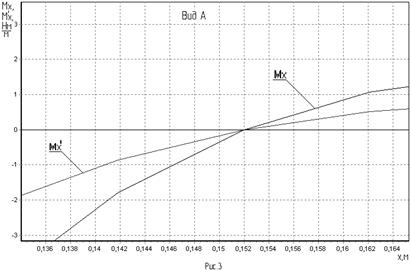
Результаты расчёта
заносим в таблицу 1 и вычерчиваем график функции ![]() (рис.2,
рис.3).
(рис.2,
рис.3).
С использованием графика ![]() определяем координату
определяем координату ![]() второй точки пересечения
графика функции
второй точки пересечения
графика функции ![]() с осью абсцисс и
находим минимальное расстояние между шпангоутами
с осью абсцисс и
находим минимальное расстояние между шпангоутами ![]() :
:
![]()
![]()
![]()
Расчётная схема 2. Расчёт подкреплённой оболочки с податливыми (упругими) шпангоутами
Найдём площадь
поперечного сечения шпангоута ![]() :
:
![]()
![]()
Определим коэффициент
податливости шпангоута ![]() :
:
![]()
![]()
Погонный изгибающий
момент по длине оболочки ![]() с
учётом податливости шпангоута:
с
учётом податливости шпангоута:
![]()
Результаты вычислений
заносим в таблицу 1 и строим график функции ![]() ,
совмещённый с графиком
,
совмещённый с графиком ![]() (рис.2, рис.3).
(рис.2, рис.3).
Определим в процентах
снижение величины изгибающего момента ![]() при
учёте податливости шпангоута:
при
учёте податливости шпангоута:
![]() ;
;
![]()
Таблица 1
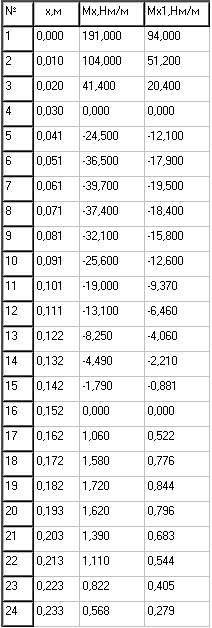
2. ИССЛЕДОВАНИЕ НАПРЯЖЁННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ПОЛУСФЕРИЧЕСКОЙ ОБОЛОЧКИ, ЗАПОЛНЕННОЙ ЖИДКОСТЬЮ
Условие задачи: Тонкостенный сосуд (рис.1), выполненный в виде полусферы, частично заполнен жидкостью. Закрепление оболочки по диаметру окружности – свободное.
Цель расчета:
1. Построить эпюры
погонных меридиональных ![]() и
кольцевых
и
кольцевых ![]() усилий.
усилий.
2. Определить толщину стенки оболочки, без учёта её собственного веса.
Исходные данные:
Радиус сферы: ![]() м;
м;
Угол зеркала жидкости: ![]() ;
;
Плотность жидкости
(горючее):![]() ;
;
Коэффициент безопасности ![]() ;
;
Материал оболочки:
Марка ВТ6С (О);
предел прочности ![]() .
.
Выполнение расчёта
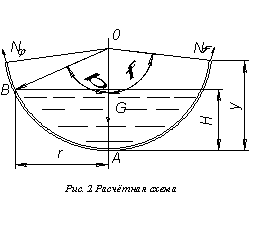
1. Расчёт участка оболочки над уровнем жидкости
Рассмотрим участок
оболочки ![]() (рис. 1). На расстоянии
(рис. 1). На расстоянии ![]() от полюса
от полюса ![]() отсекаем часть оболочки нормальным
коническим сечением с углом широты
отсекаем часть оболочки нормальным
коническим сечением с углом широты ![]() (рис.
2).
(рис.
2).
1.1 Определяем границы
участка BC: ![]() .
.
1.2 Составляем уравнение равновесия внешних и внутренних сил в проекции на вертикальную ось для отсечённой части оболочки:
![]() ,
,
где ![]() - вес жидкости, заполняющей
полусферу;
- вес жидкости, заполняющей
полусферу; ![]() - координаты расчётного
сечения;
- координаты расчётного
сечения; ![]() - меридиональная погонная
сила.
- меридиональная погонная
сила.
1.3 Определяем высоту столба жидкости в полусферической оболочке:
![]()
1.4 Находим объём шарового сегмента, заполненного жидкостью:
![]()
1.5 Вычисляем вес жидкости по формуле:
![]()
1.6 Определяем текущий радиус кольцевого сечения оболочки:
![]()
1.7 Находим погонное
меридиональное усилие ![]() из уравнения
равновесия отсечённой части оболочки:
из уравнения
равновесия отсечённой части оболочки:
![]() .
.
1.8 Определяем погонное
кольцевое усилие ![]() для участка
для участка ![]() , используя уравнение
Лапласа:
, используя уравнение
Лапласа:
![]() ,
,
где ![]() ,
, ![]() – главные радиусы кривизны
расчётного сечения оболочки;
– главные радиусы кривизны
расчётного сечения оболочки;
![]() – интенсивность внешней нагрузки на
стенку в расчётном сечении оболочки.
– интенсивность внешней нагрузки на
стенку в расчётном сечении оболочки.
Для сферы R1 = R2 и для участка ![]()
![]()
![]() = -
= -![]() .
.
Результаты расчёта
заносим в таблицу 1 при условии ![]() .
.
Таблица 1
| № точки |
|
|
|
| 1 | 90 | 1035 | -1035 |
| 2 | 87 | 1037 | -1037 |
| 3 | 84 | 1046 | -1046 |
| 4 | 81 | 1061 | -1061 |
| 5 | 78 | 1081 | -1081 |
| 6 | 75 | 1109 | -1109 |
| 7 | 72 | 1144 | -1144 |
| 8 | 69 | 1187 | -1187 |
| 9 | 66 | 1240 | -1240 |
| 10 | 63 | 1303 | -1303 |
| 11 | 60 | 1380 | -1380 |
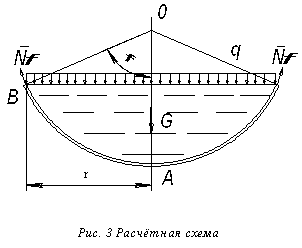
2. Расчёт участка оболочки под уровнем жидкости
Рассмотрим участок
оболочки ![]() (рис.1). Построим нормальное
коническое сечение на расстоянии
(рис.1). Построим нормальное
коническое сечение на расстоянии ![]() от
полюса оболочки. Положение расчётного сечения определяется углом широты
от
полюса оболочки. Положение расчётного сечения определяется углом широты![]()
2.1 Определим границы
участка ![]() :
: ![]() .
.
2.2 Составляем уравнение равновесия внешних и внутренних сил в проекции на вертикальную ось для отсечённой части оболочки:
![]() ,
,
где ![]() - вес жидкости, заключённой
в шаровом сегменте высотой
- вес жидкости, заключённой
в шаровом сегменте высотой ![]() ;
; ![]() - давление жидкости в расчётном
сечении;
- давление жидкости в расчётном
сечении; ![]() - площадь поперечного
сечения оболочки на уровне
- площадь поперечного
сечения оболочки на уровне ![]() ;
; ![]() - радиус поперечного
сечения оболочки на уровне
- радиус поперечного
сечения оболочки на уровне ![]() .
.
2.3 Определяем составляющие уравнения равновесия:
Объём шарового сегмента:
![]() ,
,
где ![]() .
.
Вес жидкости: ![]() .
.
Давление жидкости на
уровне ![]() от зеркала жидкости:
от зеркала жидкости:
![]() .
.
Площадь поперечного сечения
![]() ,
,
где ![]() .
.
Значения составляющих уравнения равновесия заносим в таблицу 2.
Таблица 2
| № точки |
|
Vшс, м3 |
G, Н | q, Па |
S, м2 |
r, м |
| 1 | 60 | 0,932 | 7313 | 0 | 3,443 | 0,974 |
| 2 | 54 | 0,656 | 5145 | 775,06 | 3,217 | 0,910 |
| 3 | 48 | 0,436 | 3419 | 1493 | 2,955 | 0,836 |
| 4 | 42 | 0,270 | 2118 | 2147 | 2,661 | 0,753 |
| 5 | 36 | 0,153 | 1199 | 2728 | 2,337 | 0,661 |
| 6 | 30 | 0,077 | 601,96 | 3232 | 1,988 | 0,563 |
| 7 | 24 | 0,032 | 254,83 | 3651 | 1,617 | 0,458 |
| 8 | 18 | 0,011 | 82,72 | 3982 | 1,229 | 0,348 |
| 9 | 12 | 0,00212 | 16,64 | 4222 | 0,827 | 0,234 |
| 10 | 6 | 0,000134 | 1,05 | 4366 | 0,416 | 0,118 |
| 11 | 0 | 0 | 0 | 4415 | 0 | 0 |
2.4 Подставим найденные
значения ![]() в уравнение равновесия
и определим меридиональное усилие
в уравнение равновесия
и определим меридиональное усилие
![]() :
: ![]() .
.
2.5 Получим выражение для
погонного кольцевого усилия ![]() из
уравнения Лапласа при
из
уравнения Лапласа при
R1 = R2 = R,
![]() .
.
Результаты расчёта
заносим в таблицу 3 при условии ![]() .
.
Таблица 3
| № точки | φ, град. |
|
|
| 1 | 60 | 1380 | -1380 |
| 2 | 54 | 1548 | -676,2 |
| 3 | 48 | 1716 | -35,93 |
| 4 | 42 | 1877 | 538,4 |
| 5 | 36 | 2026 | 1,044 |
| 6 | 30 | 2158 | 1477 |
| 7 | 24 | 2272 | 1836 |
| 8 | 18 | 2363 | 2118 |
| 9 | 12 | 2429 | 2320 |
| 10 | 6 | 2470 | 2442 |
| 11 | 0 | 2483 | 2483 |
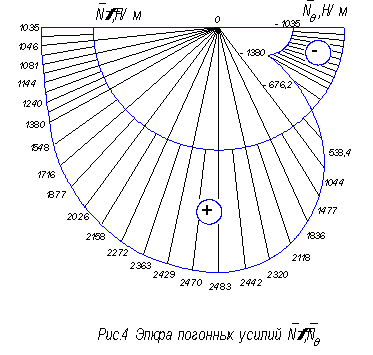
По данным таблиц строим эпюры погонных усилий. Схема эпюры приведена на рис. 4.
С помощью эпюры определяем наиболее напряжённое сечение оболочки и максимальные усилия
![]() .
.
3. Определение толщины стенки оболочки
3.1 Найдём допускаемое напряжение материала оболочки:
![]()
3.2 Определим толщину стенки:
![]() ,
,
![]()
3. ИССЛЕДОВАНИЕ НАПРЯЖЁННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ СФЕРИЧЕСКОЙ ОБОЛОЧКИ, ЗАПОЛНЕННОЙ ЖИДКОСТЬЮ
Условие задачи: Построить эпюры безмоментных
напряжений ![]() и
и ![]() для сферического сосуда
(рис. 1), полностью заполненного жидкостью.
для сферического сосуда
(рис. 1), полностью заполненного жидкостью.
Исходные данные:
Радиус оболочки: ![]() м;
м;
Плотность жидкости (окислитель):
![]() ;
;
Толщина стенки оболочки:
![]() .
.
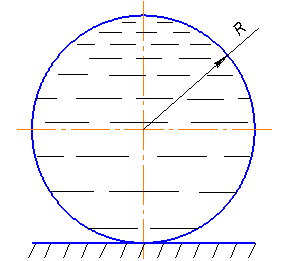
Рис. 1. Схема оболочки
Выполнение расчёта
1. Выводы расчётных зависимостей для верхней полусферы
В верхней полусфере
отсечём часть оболочки нормальным коническим сечением с углом ![]() при вершине конуса и
составим уравнение равновесия отсеченной части оболочки (рис. 2):
при вершине конуса и
составим уравнение равновесия отсеченной части оболочки (рис. 2):
![]() ,
,
где ![]() – равнодействующая сил
давления жидкости
– равнодействующая сил
давления жидкости ![]() на стенку
оболочки в проекции на
на стенку
оболочки в проекции на
вертикальную ось.
Жидкость действует на стенку оболочки переменным давлением. Равнодействующую сил давления жидкости на вертикальную ось определим по формуле:
![]() ,
,
где ![]() – объём цилиндра;
– объём цилиндра; ![]() – объём шарового сегмента,
рис. 2.
– объём шарового сегмента,
рис. 2.
![]()
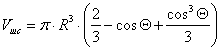 ,
,
где ![]() - высота столба жидкости в
расчётном сечении.
- высота столба жидкости в
расчётном сечении.
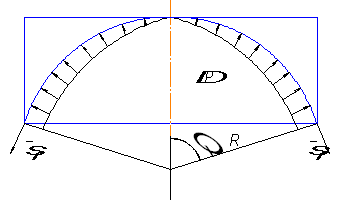
Рис. 2. Расчётная схема
Получаем:
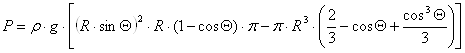 .
.
Из уравнения равновесия
после подстановки выражения для силы ![]() имеем:
имеем:
![]() .
.
Отсюда меридиональное напряжение:
![]() .
.
Определим кольцевое
напряжение ![]() . Для этого обратимся к
уравнению Лапласа, учитывая, что для сферической оболочки R1=R2=R::
. Для этого обратимся к
уравнению Лапласа, учитывая, что для сферической оболочки R1=R2=R::
![]() ,
,
где ![]() - давление жидкости в
рассматриваемом сечении оболочки.
- давление жидкости в
рассматриваемом сечении оболочки.
После подстановки в
уравнение Лапласа ![]() получаем:
получаем:
![]() .
.
Принимая угол ![]() в диапазоне от 0˚ до
90˚, занесём значения составляющих уравнения равновесия, кольцевых и
меридиональных напряжений с шагом угла
в диапазоне от 0˚ до
90˚, занесём значения составляющих уравнения равновесия, кольцевых и
меридиональных напряжений с шагом угла ![]() ,
равным 10˚,в таблицу 1.
,
равным 10˚,в таблицу 1.
Таблица 1
|
|
|
|
|
|
|
|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 0,002049 | 0,001027 | 11,445 | 191,409 |
2,442 |
7,350 |
| 20 | 0,032 | 0,016 | 174,869 | 759,818 |
9,616 |
2,925 |
| 30 | 0,15 | 0,077 | 818,854 | 1688 |
2,107 |
6,528 |
| 40 | 0,432 | 0,226 | 2314 | 2948 |
3,603 |
1,148 |
| 50 | 0,938 | 0,503 | 4870 | 4501 |
5,338 |
1,768 |
| 60 | 1,677 | 0,932 | 8349 | 6300 |
7,161 |
2,506 |
| 70 | 2,599 | 1,512 | 12170 | 8290 |
8,869 |
3,354 |
| 80 | 3,585 | 2,213 | 15360 | 10410 |
1,019 |
4,307 |
| 90 | 4,473 | 2,982 | 16700 | 12600 |
1,074 |
5,371 |
2. Выводы расчётных зависимостей для нижней полусферы
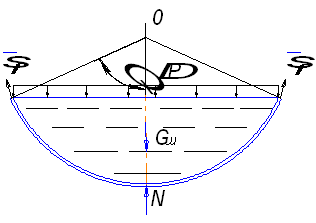
Рис. 3. Расчётная схема
Отсечём нормальным
коническим сечением часть сферы (рис. 3). Вес жидкости в объёме шарового
сегмента ![]() и равнодействующая от
гидростатического давления жидкости
и равнодействующая от
гидростатического давления жидкости ![]() , находящейся
выше рассматриваемого сечения, уравновешиваются реакцией опоры N и результирующим меридиональным
усилием от погонных меридиональных сил, распределённых по круговому контуру
шарового сегмента в сечении
, находящейся
выше рассматриваемого сечения, уравновешиваются реакцией опоры N и результирующим меридиональным
усилием от погонных меридиональных сил, распределённых по круговому контуру
шарового сегмента в сечении ![]() . Отсюда
получим следующее уравнение равновесия:
. Отсюда
получим следующее уравнение равновесия:
![]() ,
,
где ![]() - реакция опоры, равная
весу жидкости в объёме шара.
- реакция опоры, равная
весу жидкости в объёме шара.
![]() Н;
Н;
![]() - гидростатическое давление
жидкости;
- гидростатическое давление
жидкости;
![]() - площадь поперечного сечения;
- площадь поперечного сечения;
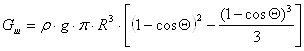 - вес жидкости в объёме шарового сегмента.
- вес жидкости в объёме шарового сегмента.
После подстановки получим:
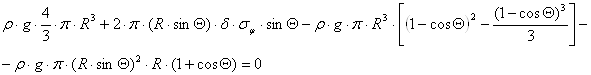
Отсюда имеем:
![]() .
.
Для нижней части
полусферы ![]() определяем из уравнения
Лапласа:
определяем из уравнения
Лапласа:
![]() , где
, где ![]() .
.
Отсюда:
![]() .
.
Принимая угол ![]() в диапазоне от 90˚ до
0˚, занесём значения составляющих уравнения равновесия, кольцевых и
меридиональных напряжений с шагом угла
в диапазоне от 90˚ до
0˚, занесём значения составляющих уравнения равновесия, кольцевых и
меридиональных напряжений с шагом угла ![]() ,
равным 10˚,в таблицу 2.
,
равным 10˚,в таблицу 2.
Таблица 2
|
|
|
S, м2 |
|
|
|
| 90 | 12600 | 3,976 | 33410 |
1,074 |
5,371 |
| 80 | 14790 | 3,856 | 24790 |
9,958 |
6,568 |
| 70 | 16910 | 3,511 | 16940 |
6,922 |
7,957 |
| 60 | 18910 | 2,982 | 10440 |
-1,908 |
9,667 |
| 50 | 20700 | 2,333 | 5633 |
-1,411 |
1,2 |
| 40 | 22260 | 1,643 | 2529 |
-4,314 |
1,57 |
| 30 | 23520 | 0,994 | 859,303 |
-1,095 |
2,298 |
| 20 | 24450 | 0,465 | 178,593 |
-3,038 |
4,288 |
| 10 | 25020 | 0,12 | 11,508 |
-1,361 |
1,489 |
| 0 | 25210 | 0 | 0 |
-1,362 |
1,362 |
Выводы
В опорной точке сферы
безмоментные напряжения обращаются в бесконечность. Это является следствием
обращения в ноль площади сечения, по которой действуют напряжения ![]() . В реальных условиях
сосредоточенных в точке сил не существует, и поэтому эта особенность имеет
место лишь в расчётной схеме.
. В реальных условиях
сосредоточенных в точке сил не существует, и поэтому эта особенность имеет
место лишь в расчётной схеме.
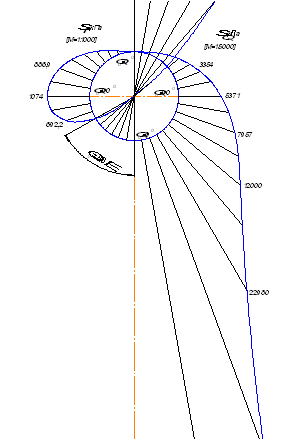
Рис. 4. Эпюра напряжений ![]() и
и ![]()
4. РАСЧЁТ СФЕРИЧЕСКОГО ТОПЛИВНОГО БАКА С ОПОРОЙ ПО ЭКВАТОРУ
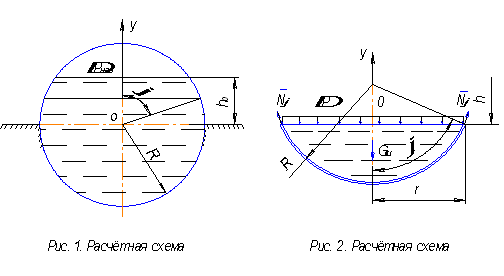
Условие задачи: Сферический топливный бак с опорой по экватору, заполненный жидкостью, находится под давлением наддува (рис.1, рис. 2).
Цель расчёта: Определить толщину стенки и массу конструкции бака при заданных размерах и нагрузке.
Исходные данные:
Радиус оболочки: ![]() м;
м;
Плотность жидкости
(горючее): ![]() ;
;
Давление наддува: ![]() ;
;
Уровень жидкости: ![]() ;
;
Коэффициент осевой
перегрузки: ![]() ;
;
Коэффициент безопасности:
![]() ;
;
Материал оболочки:
марка ВТ6С (О);
предел прочности ![]() ;
;
плотность ![]() .
.
Примечание: Для упрощения принимаем: ![]() .
.
Выполнение расчёта
1. Расчёт оболочки над опорой
Формулы для расчёта
погонных меридиональных ![]() и
кольцевых
и
кольцевых ![]() усилий над опорой
усилий над опорой ![]() от действия давления
жидкости и давления наддува имеют вид:
от действия давления
жидкости и давления наддува имеют вид:
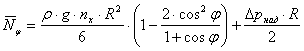 ;
;
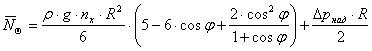 ,
,
где ![]() – угол, отсчитываемый в
плоскости меридиана от верхнего полюса;
– угол, отсчитываемый в
плоскости меридиана от верхнего полюса;
![]() – ускорение свободного падения.
– ускорение свободного падения.
Принимая угол ![]() в диапазоне от 0˚ до
90˚, занесём значения кольцевых и меридиональных усилий с шагом угла
в диапазоне от 0˚ до
90˚, занесём значения кольцевых и меридиональных усилий с шагом угла ![]() , равным 10˚,в таблицу
1.
, равным 10˚,в таблицу
1.
Таблица 1
|
|
|
|
| 0 | 140600 | 140600 |
| 10 | 140800 | 141000 |
| 20 | 141100 | 142200 |
| 30 | 141800 | 144100 |
| 40 | 142600 | 146800 |
| 50 | 143500 | 150200 |
| 60 | 144500 | 154100 |
| 70 | 145400 | 158700 |
| 80 | 146100 | 163900 |
| 90 | 146400 | 169600 |
2. Расчёт оболочки под опорой
Выведем расчётные формулы
для погонных меридиональных и кольцевых усилий от действия давления жидкости и
давления наддува под опорой топливного бака ![]() .
Составим уравнение равновесия внешних и внутренних сил для выделенного сечения
оболочки (рис. 2) в проекции на вертикальную ось
.
Составим уравнение равновесия внешних и внутренних сил для выделенного сечения
оболочки (рис. 2) в проекции на вертикальную ось ![]() .
Получим:
.
Получим:
![]() ,
,
где ![]() – давление в
рассматриваемом сечении; S
– площадь расчётного поперечного сечения;
– давление в
рассматриваемом сечении; S
– площадь расчётного поперечного сечения;
![]() – вес жидкости в шаровом сегменте,
отсечённом нормальным коническим сечением с углом
– вес жидкости в шаровом сегменте,
отсечённом нормальным коническим сечением с углом ![]() ;
;
![]() – равнодействующая погонных
меридиональных усилий
– равнодействующая погонных
меридиональных усилий ![]() в проекции на
ось
в проекции на
ось ![]() .
.
Давление ![]() в произвольном сечении
оболочки равно давлению наддува плюс давление столба жидкости над
рассматриваемым сечением:
в произвольном сечении
оболочки равно давлению наддува плюс давление столба жидкости над
рассматриваемым сечением:
![]() ,
,
где h – высота столба жидкости от зеркала жидкости до расчётного сечения.
![]() ,
,
![]() ,
,
где ![]() - радиус рассматриваемого
сечения.
- радиус рассматриваемого
сечения.
Определим вес жидкости в
шаровом сегменте: ![]() ,
,
где ![]() – объём шарового сегмента,
отсечённого нормальным коническим сечением с углом
– объём шарового сегмента,
отсечённого нормальным коническим сечением с углом ![]() .
.
![]() .
.
Спроектируем погонные
меридиональные усилия ![]() в расчётном
сечении на вертикальную ось
в расчётном
сечении на вертикальную ось ![]() :
: ![]() .
.
Величина равнодействующей
![]() от распределённых по
кольцу радиуса r меридиональных
сил
от распределённых по
кольцу радиуса r меридиональных
сил ![]() определяется по формуле:
определяется по формуле:
![]() .
.
Окончательно получаем ![]() .
.
Принимая угол ![]() в диапазоне от 90˚ до
0˚, занесём значения составляющих уравнения равновесия с шагом угла
в диапазоне от 90˚ до
0˚, занесём значения составляющих уравнения равновесия с шагом угла ![]() , равным 10˚,в таблицу
2.
, равным 10˚,в таблицу
2.
Таблица 2
|
|
|
S, м2 |
|
|
| 90 | 0,2809 | 3,976 | 2,982 | 81910 |
| 80 | 0,2863 | 3,856 | 2,213 | 60790 |
| 70 | 0,2915 | 3,511 | 1,512 | 41530 |
| 60 | 0,2964 | 2,982 | 0,932 | 25600 |
| 50 | 0,3008 | 2,333 | 0,503 | 13810 |
| 40 | 0,3046 | 1,643 | 0,226 | 6201 |
| 30 | 0,3077 | 0,994 | 0,077 | 2107 |
| 20 | 0,3099 | 0,465 | 0,016 | 437,881 |
| 10 | 0,3113 | 0,120 | 0,001027 | 28,215 |
| 0 | 0,3118 | 0 | 0 | 0 |
Подставляем полученные
выражения ![]() , S,
, S, ![]() ,
,
![]() в уравнение равновесия и
преобразовываем.
в уравнение равновесия и
преобразовываем.
Получаем формулу для вычисления погонных меридиональных усилий:
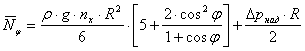 .
.
Подставляя полученное
выражение ![]() в уравнение Лапласа,
определим погонные кольцевые усилия
в уравнение Лапласа,
определим погонные кольцевые усилия ![]() .
Уравнения Лапласа в усилиях имеет вид:
.
Уравнения Лапласа в усилиях имеет вид:
![]() ,
,
где ![]() ,
,![]() – главные радиусы кривизны
оболочки;
– главные радиусы кривизны
оболочки; ![]() – давление в
рассматриваемом сечении.
– давление в
рассматриваемом сечении.
Для сферического бака R1 = R2 = R, поэтому уравнение Лапласа принимает вид:
![]() .
.
Подставив выражение ![]() в уравнение Лапласа и
проведя преобразования, получим формулу для вычисления
в уравнение Лапласа и
проведя преобразования, получим формулу для вычисления ![]() :
:
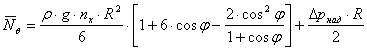 .
.
Принимая угол ![]() в диапазоне от 90˚ до
0˚, занесём значения составляющих уравнения равновесия с шагом угла
в диапазоне от 90˚ до
0˚, занесём значения составляющих уравнения равновесия с шагом угла ![]() , равным 10˚,в таблицу
3.
, равным 10˚,в таблицу
3.
Таблица 3
|
|
|
|
| 90 | 169600 | 146400 |
| 80 | 169900 | 152200 |
| 70 | 170600 | 157300 |
| 60 | 171500 | 161900 |
| 50 | 172500 | 165900 |
| 40 | 173400 | 169200 |
| 30 | 174300 | 171900 |
| 20 | 174900 | 173800 |
| 10 | 175300 | 175000 |
| 0 | 175400 | 175400 |
Погонные усилия в
сферическом баке принимают наибольшее значение в нижнем полюсе. Кроме того, в
нижнем полюсе ![]() =
= ![]() . Сравнивая результаты
вычислений значений
. Сравнивая результаты
вычислений значений ![]() ,
, ![]() на экваторе для участков
над опорой и под опорой, делаем вывод: усилия
на экваторе для участков
над опорой и под опорой, делаем вывод: усилия ![]() ,
,
![]() терпят разрыв.
терпят разрыв.
Определение толщины стенки бака
Расчёт на прочность производим по максимальным погонным усилиям.
Определяем напряжения в
нижнем полюсе бака: ![]() ,
,
где ![]() – толщина стенки бака.
– толщина стенки бака.
Подставив в эти формулы выражения для погонных меридиональных и кольцевых усилий, получим:
![]() .
.
Минимальную толщину оболочки можно получить по формуле:
![]() ,
,
где ![]() – допускаемые напряжения.
– допускаемые напряжения.
Определяем массу оболочки бака:
![]() ,
,
где ![]() – площадь поверхности
оболочки;
– площадь поверхности
оболочки;
![]() – плотность материала оболочки.
– плотность материала оболочки.
Построим эпюру погонных
усилий ![]() ,
,![]() (рис. 3):
(рис. 3):
Рис. 3. Эпюра погонных
усилий ![]() ,
,![]()
5. РАСЧЁТ БАКА НА ПРОЧНОСТЬ
Условие задачи: Цилиндрический бак с верхним
полуэллиптическим и нижним полусферическими днищами (рис.1) находится под
действием давления наддува ![]() и заполнен
жидкостью до уровня H.
и заполнен
жидкостью до уровня H.
Цель расчёта:
1. Определить величину
безмоментных напряжений ![]() ;
;
2. Определить толщину обечайки и днищ бака.
Исходные данные:
Радиус бака: ![]() м;
м;
Размеры эллиптического
днища: ![]()
![]()
Высота столба жидкости: ![]() ;
;
Плотность жидкости
(окислитель): ![]() ;
;
Давление наддува: ![]() ;
;
Коэффициент безопасности:
![]() ;
;
Материал оболочки:
марка ВТ6С (О);
предел прочности ![]() ;
;
![]() .
.
Выполнение расчёта
Участок верхнего эллиптического днища
Рис. 2. Схема эллиптического днища
В днище нормальным
коническим сечением I – I отсечём
верхнюю часть оболочки и составим для неё уравнение равновесия. Выбираем оси
координат так, как показано на рис. 2. Из уравнения равновесия и уравнения
Лапласа получаем выражения для ![]() в расчётном
сечении эллиптического днища в виде:
в расчётном
сечении эллиптического днища в виде:
![]()
![]() ,
,
где ![]() ,
, ![]() – радиусы кривизны
рассматриваемого сечения оболочки,
– радиусы кривизны
рассматриваемого сечения оболочки,
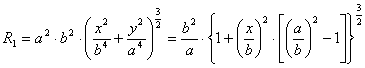 ,
,
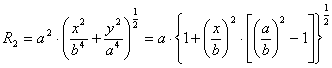 ,
,
где x, y – координаты точки в рассматриваемом сечении оболочки.
Для построения эпюр
задаёмся значениями x. Координату y определяем из уравнения эллипса ![]() . Отсюда получаем
. Отсюда получаем
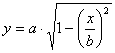 .
.
Меньшую полуось b разбиваем на 5 равных частей, для каждого сечения производим расчёты, результаты расчётов заносим в таблицу 1.
Таблица 1
| № сечения |
x, м |
y, м |
R1, м |
R2, м |
|
|
| 1 | 0 | 1,125 | 0,18 | 1,125 |
|
|
| 2 | 0,09 | 1,102 | 0,24 | 1,238 |
|
|
| 3 | 0,18 | 1,031 | 0,449 | 1,526 |
|
|
| 4 | 0,27 | 0,9 | 0,884 | 1,913 |
|
|
| 5 | 0,36 | 0,675 | 1,639 | 2,349 |
|
|
| 6 | 0,45 | 0 | 2,813 | 2,813 |
|
|
Участок цилиндра над зеркалом жидкости
Рис. 3. Сечение II – II
Нормальным сечением к оси бака II – II отсечём часть цилиндра, расположенную над зеркалом жидкости (рис. 3). Составим уравнение равновесия для верхней отсеченной части оболочки в проекции на вертикальную ось:
![]() .
.
Отсюда меридиональное напряжение:
![]() Па.
Па.
Для цилиндра ![]() ;
; ![]() , поэтому из уравнения
Лапласа получаем кольцевое напряжение:
, поэтому из уравнения
Лапласа получаем кольцевое напряжение:
![]() Па.
Па.
Участок цилиндра под зеркалом жидкости
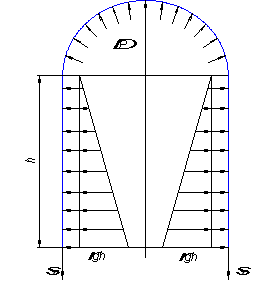
Рис. 4. Сечение III – III
Для сечения III – III расчётная схема (рис. 4) будет отличаться от показанной на рис. 3 тем, что здесь необходимо дополнительно учесть давление на стенку цилиндрической части бака со стороны жидкости.
Уравнение равновесия в проекции на вертикальную ось бака остаётся без изменений:
![]() .
.
Поэтому меридиональное напряжение не меняется:
![]() Па.
Па.
Окружное напряжение определяем из уравнения Лапласа
![]() ,
,
где ![]() Па.
Па.
Отсюда ![]() Па.
Па.
Участок нижнего полусферического днища
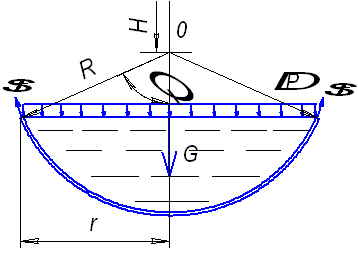
Рис. 5. Сечение IV – IV
Для нижнего днища
нормальным коническим сечением IV – IV
с углом ![]() при вершине отсечём нижнюю
часть сферической оболочки (рис. 5). Составим для неё уравнение равновесия
внешних и внутренних сил в проекции на вертикальную ось оболочки:
при вершине отсечём нижнюю
часть сферической оболочки (рис. 5). Составим для неё уравнение равновесия
внешних и внутренних сил в проекции на вертикальную ось оболочки:
![]() ,
,
где r – радиус кольцевого сечения
оболочки, ![]() ;
;
S – площадь поперечного сечения, ![]() ;
;
![]() - давление в расчётном сечении
оболочки,
- давление в расчётном сечении
оболочки, ![]() ;
;
G – вес жидкости в объёме шарового
сегмента, ![]() ;
;
Vc – объём шарового сегмента, ![]() .
.
Подставляя значения r, S, ![]() , G в уравнение равновесия определяем меридиональное напряжение
, G в уравнение равновесия определяем меридиональное напряжение ![]() :
:
![]()
Уравнение Лапласа для сферической оболочки имеет вид:
![]() .
.
Подставляя в уравнение
Лапласа ![]() , находим кольцевое
напряжение
, находим кольцевое
напряжение ![]() в сечении IV – IV:
в сечении IV – IV:
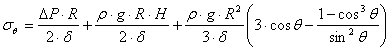 .
.
Построим таблицу 2
значений ![]() и
и ![]() в зависимости от угла
в зависимости от угла ![]() в диапазоне от 0˚ до
90˚ с шагом в 15˚:
в диапазоне от 0˚ до
90˚ с шагом в 15˚:
Таблица 2
|
|
|
|
| 0 |
|
|
| 15 |
|
|
| 30 |
|
|
| 45 |
|
|
| 60 |
|
|
| 75 |
|
|
| 90 |
|
|
По полученным напряжениям
в характерных сечениях бака строим эпюры напряжений ![]() и
и
![]() (рис. 6).
(рис. 6).
Определение толщины стенок бака
Для определения толщины днищ и обечайки бака используем следующее условие:
σmax ≤ [σ], где [σ] = ![]() Па
Па
Толщина стенки ![]() .
.
Получаем: для верхнего
днища ![]() м;
м;
для обечайки бака ![]() м;
м;
для нижнего днища ![]() м.
м.
Из расчётов видно, что δmax = δ2 = 0,518 мм – окончательная толщина стенки бака. По расчётной толщине стенки подбираем толщину листа согласно ГОСТ 22178 – 76:
![]() .
.
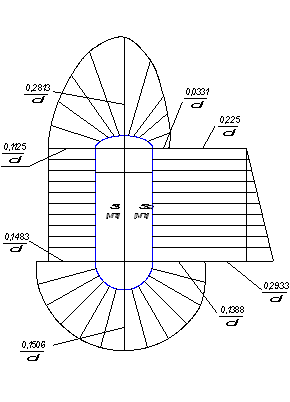
Рис.6. Эпюры безмоментных
напряжений ![]() и
и ![]()
Список литературы
1. Расчёт безмоментных оболочек: Методические указания по дисциплине “Основы расчёта оболочек” для специальностей: 130600-Ракетостроение, 130400-Ракетные двигатели/ Сост. Л.И. Гречух, И. Н. Гречух.- Омск: Изд-во ОмГТУ, 2002.- 32 с.