Курсовая работа: Привод конвейера ПК-19
Введение
Конвейер типа ПК-19 предназначен для перемещения сыпучих материалов в горизонтальном направлении.
Строгание осуществляется резцом, закреплённым в резцовой головке, которая возвратно–поступательно движется совместно с ползуном.
В поперечно–строгальный станок входят рычажный, зубчатый и кулачковый механизмы. Целью данного курсового проекта является синтез каждого из узлов по заданным параметрам.
Для перемещения ползуна используется кулисный механизм с качающейся кулисой, состоящий из кривошипа, камня, шатуна и ползуна. Кулисный механизм предназначен для преобразования вращательного движения в поступательное движение.
Электродвигатель через планетарный механизм и одноступенчатую рядовую зубчатую передачу приводит в движение кривошип кулисного механизма. Зубчатый механизм предназначен для понижения оборотов двигателя до оборотов кривошипа.
На одном валу с кривошипом насажен кулачковый механизм, который приводит в движение толкатель, связанный с механизмом смазки станка и регулирует подачу смазочного материала в зону смазки.
1. Синтез и анализ рычажного механизма
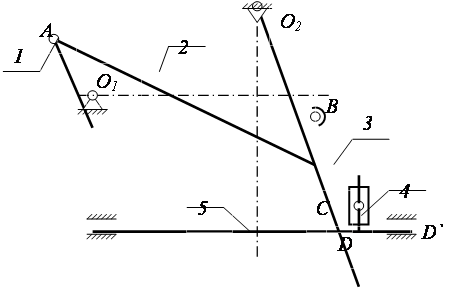
Рисунок 1 - Схема механизма:
Исходные данные :
1. Координаты центра вращения кривошипа
![]()
2.Длина звена О2С
![]()
3.Расстояние между точками О2 и В
![]()
4.Угол отклонения звена О2С от оси симметрии
![]()
5.Частота вращения кривошипа
![]()
6.![]() ;
; ![]()
1.1 Структурный анализ механизма
Механизм состоит из пяти подвижных звеньев: кривошипа 1, шатуна 2, коромысла 3, камня 4, ползуна 5. Все звенья, соединяясь между собой, образуют 7 кинематических пар: вращательных в точках О1, А, В, О2, С и поступательных в точках D и D`.
Определим степень подвижности механизма по формуле Чебышева:
![]()
где р1 – количество одноподвижных кинематических пар, р2 – количество двуподвижных кинематических пар. Поскольку в данном механизме имеется только 7 шарнирных соединений, то р1=7, р2=0. Откуда
![]()
К начальному звену 1 присоединены последовательно группы Ассура: (2,3) – второго класса, второго порядка, и (4,5) – второго класса, второго порядка. Ниже показано разложение механизма на структурные группы Ассура:

 О2
О2
О1 A C
B
D D`
Рисунок 2 - Разложение механизма на структурные группы Ассура:
Формула механизма:
![]() .
.
По классификации Артоболевского – механизм второго класса, второго порядка.
1.2 Определение недостающих размеров
Недостающие размеры определим графическим способом – построением планов механизма. Выбираем масштабный коэффициент построения планов механизма:
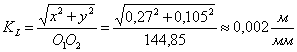
В масштабе КL по заданным значениям координат X и Y на чертеже наносят точки О1 и О2, и строят крайние положения О2В0 и О2В0` коромысла О2В. Соединив точку О1 (центр вращения кривошипа) с точками В0 и В0` получим два крайних положения механизма – ближнее О1В0О2 и дальнее О1В0`О2.

АВ + О1А = О1В0`
АВ - О1А = О1В0
В полученной системе двух линейных уравнений с двумя неизвестными правые части известны, так как О1В0` и О1В0 можно измерить на чертеже, в мм. Решая полученную систему уравнений совместно, определяют длину шатуна и кривошипа
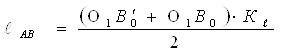 ,
,
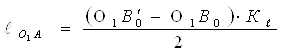 .
.
где О1В0 и О1В0` - отрезки, измеренные на чертеже, мм,
КL – масштабный коэффициент длин, м/мм.
1.3 Построение планов скоростей
Определяем скорость конца кривошипа (А), допуская, что ω1=const, то скорость точки А для всех положений постоянна.
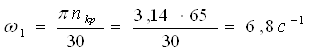
n=65 - число оборотов кривошипа.
![]()
Скорость точки А кривошипа изображаем на плане в виде отрезка РVа=44мм. В таком случае, масштабный коэффициент плана скоростей
![]()
Вектор РVа направляем перпендикулярно текущему положению кривошипа и по направлению вращения. Для определения скорости точки В составим систему векторных уравнений, решая которую, получим отрезок PVb – изображение скорости точки В:

Откуда
![]() ,
, ![]() .
.
Для первого положения механизма имеем
![]() ,
, ![]() .
.
Скорость точки С (отрезок PVc) определим из свойства подобия плана скоростей:
![]()
![]()
Для первого положения механизма получаем
![]()
![]() .
.
Для определения скорости точки D составим систему уравнений:
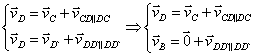
Решая графически эту систему уравнений, получим отрезок PVd на плане скоростей, изображающий скорость точки D. Для первого положения механизма имеем PVd=40,91 мм,
![]() .
.
После построения планов скоростей имеем:
Таблица 1.1. Значения скоростей.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| VA, м/с | 0,44 | |||||||||||
| VВ, м/с | 0,29 | 0,42 | 0,44 | 0,36 | 0,22 | 0,05 | 0,13 | 0,31 | 0,47 | 0,53 | 0,34 | 0 |
| VC, м/с | 0,43 | 0,63 | 0,66 | 0,54 | 0,33 | 0,08 | 0,19 | 0,46 | 0,70 | 0,79 | 0,52 | 0 |
| VD, м/с | 0,41 | 0,62 | 0,66 | 0,53 | 0,32 | 0,07 | 0,18 | 0,45 | 0,70 | 0,79 | 0,50 | 0 |
| VВА, м/с | 0,24 | 0,06 | 0,10 | 0,24 | 0,38 | 0,44 | 0,40 | 0,23 | 0,07 | 0,41 | 0,56 | 0 |
| VDC, м/с | 0,12 | 0,09 | 0,01 | 0,10 | 0,08 | 0,03 | 0,06 | 0,11 | 0,07 | 0,08 | 0,14 | 0 |
1.4 Построение планов ускорений
Планы ускорений строим, начиная с кривошипа. Кривошип совершает равномерное вращательное движение, поэтому
![]() ;
; ![]() .
.
На плане
ускорений изображаем его отрезком ![]() . Отсюда масштабный коэффициент
плана ускорений:
. Отсюда масштабный коэффициент
плана ускорений:
![]() .
.
Ускорение точки А кривошипа направляем от точки А к полюсу вращения – точке О1.
Для определения полного ускорения точки В шатуна составим систему:

Нормальные ускорения найдём по формуле:
![]() ;
;
Соответственно определяем
![]()
Решая вышеприведенную систему векторных уравнений с учётом найденных ускорений, получим полные ускорения точки В.
Полное ускорение точки С найдём по свойству подобия:
![]() .
.
Для первого положения механизма имеем
![]()
Для определения ускорения точки D составим систему векторных уравнений

и решим её графически. Решая эту систему для первого положения механизма, получаем
![]() и
и ![]() .
.
Таблица 1.2. Значения ускорений.
| 1 | 3 | 5 | 7 | 9 | 11 | 12 | |
| аА, м/с2 | 3,02 | ||||||
| аВ, м/с2 | 2,78 | 1,06 | 2,11 | 2,35 | 2,06 | 3,99 | 3,74 |
| аC, м/с2 | 4,17 | 1,59 | 3,17 | 3,53 | 3,09 | 5,99 | 5,61 |
| аD, м/с2 | 4,13 | 0,69 | 3,14 | 3,37 | 2,76 | 5,94 | 5,27 |
| аВАn, м/с2 | 0,2 | 0,03 | 0,51 | 0,58 | 0,02 | 1,10 | 0 |
| aBO2n, м/с2 | 0,4 | 0,96 | 0,24 | 0,08 | 1,10 | 0,59 | 0 |
| aBA, м/с2 | 2,56 | 1,51 | 1,38 | 1,40 | 4,64 | 1,10 | 2,08 |
| аDC, м/с2 | 0,61 | 1,43 | 0,42 | 1,03 | 1,40 | 0,79 | 1,92 |
1.5 Построение диаграмм движения выходного звена
Масштабные коэффициенты диаграмм:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
где Хt – длина отрезка на оси абсцисс, равного одному периоду.
1.6 Определение угловых скоростей и ускорений
Определим угловые скорости звеньев в первом положении механизма:
![]() ;
; ![]() ;
;
![]() ;
; 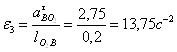
Направление угловых скоростей и ускорений – соответственно направлению и характеру вращений этих звеньев относительно точек: А (шатун) и О2 (коромысло).
1.7 Определение скоростей и ускорений центров масс звеньев
![]() ;
; ![]()
![]()
![]() ;
; ![]()
![]()
1.8 Аналитический метод расчёта

1. Расчёт ведётся для первого положения.
Составляем уравнение замкнутости векторного контура
![]()
2. В проекциях на координатные оси
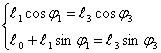
3. Разделим второе уравнение на первое
![]() ;
;
4. Берём производную от левой и правой части
![]() ;
;
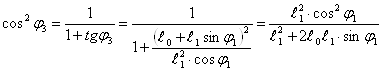
5. Найдем передаточную функцию скоростей U31
![]() ;
;
6. Передаточную функцию ускорений U'31
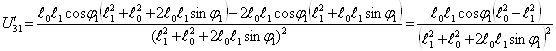 ;
;
![]()
7. Угловая скорость
![]()
8. Угловое ускорение
![]()
9.Составляем векторное уравнение для контура О2ВС
![]()
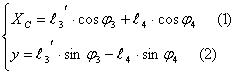 φ3=85.8°
φ3=85.8°
![]() ;
;
![]() ;
;
![]()
![]() ;
;
![]()
![]()
![]()
![]()
![]()
![]()
![]() м/с2
м/с2
![]() м/с2
м/с2
Составляем программу для вычисления скоростей и ускорений 5 звена и для построения диаграмм скорости и ускорения
Sub кинематика()
Dim f1, f3, w3, e3, sinf4, cosf4, sinf3, cosf3, U43, U431,_
Vc, ac, h, k As Double
Worksheets(1).Activate
Worksheets(1).Range("a:o").Clear
Worksheets(1).ChartObjects.Delete
Const l0 = 0.304
Const l1 = 0.104
Const l3 = 0.38
Const l4 = 0.57
Const l5 = 0.285
Const w1 = 8.37
h = 3
k = 1
For f1 = 10 * 3.14 / 180 To 370 * 3.14 / 180 Step 30 * 3.14 / 180
w3 = w1 * ((l1 ^ 2 + l0 * l1 * Sin(f1)) / (l1 ^ 2 + l0 ^ 2 + _
2 * l0 * l1 * Sin(f1)))
e3 = w1 ^ 2 * ((l0 * l1 * Cos(f1) * (l0 ^ 2 - l1 ^ 2)) / ((l1 ^ 2 + _
l0 ^ 2 + 2 * l0 * l1 * Sin(f1)) ^ 2))
sinf3 = (l0 + l1 * Sin(f1)) / (Sqr(l1 ^ 2 + l0 ^ 2 + 2 * l0 * l1 * Sin(f1)))
cosf3 = Sqr(1 - sinf3 ^ 2)
sinf4 = (l5 - l3 * sinf3) / l4
cosf4 = Sqr(1 - sinf4 ^ 2)
U43 = -((l3 * cosf3) / (l4 * cosf4))
U431 = (l3 * sinf3 + l4 * sinf4 * U43) / (l4 * cosf4)
Vc = -(w3 * (-l3 * sinf3 - l4 * sinf4 * U43))
ac = -((w3 ^ 2 * (-l3 * cosf3 - l4 * sinf4 * U431 - l4 * cosf4 * U43)) + _
(e3 * (-l3 * sinf3 - l4 * sinf4 * U43)))
Worksheets(1).Cells(3, h) = Vc
Worksheets(1).Cells(8, h) = ac
Worksheets(1).Cells(2, h) = k
Worksheets(1).Cells(7, h) = k
h = h + 1
k = k + 1
Next f1
Worksheets(1).Cells(2, 2) = 0
Worksheets(1).Cells(7, 2) = 0
Worksheets(1).Cells(3, 2) = Vc
Worksheets(1).Cells(8, 2) = ac
Worksheets(1).Cells(2, 1) = "Vc, м/с"
Worksheets(1).Cells(3, 1) = "Аналитические"
Worksheets(1).Cells(7, 1) = "ac, м/с^2"
Worksheets(1).Cells(8, 1) = "Аналитические"
Worksheets(1).Cells(1, 7) = "Положения механизма"
Worksheets(1).Cells(6, 7) = "Положения механизма"
End Sub
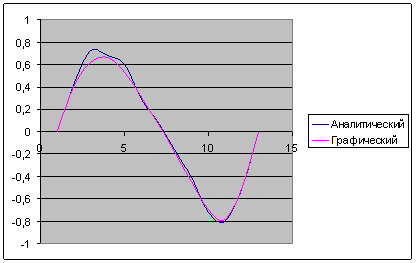
Рисунок 4 -Результаты работы программы
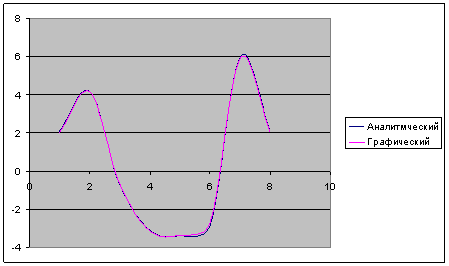
Рисунок 4 -Результаты работы программы
2. Силовой анализ механизма
Исходные данные:
Масса шатуна m2=70 кг.
Масса коромысла m3=80 кг.
Масса материала с жёлобом, m5=370 кг.
Диаметр цапф вращательных пар dц=60 мм.
Моменты инерции коромысла и шатуна
![]() ,
, ![]()
2.1 Определение сил инерции
Веса звеньев:
![]()
![]()
![]()
Сила полезного сопротивления
![]()
Силы инерции массивных звеньев и их моменты определим по формулам:
![]() и
и ![]()
![]()
![]()
![]()
![]()
При расчётах диад действие момента инерции интерпретируем как действие соответствующей силы инерции, отнесённой на одноимённое плечо от центра тяжести данного звена. Рассчитаем эти плечи по формуле:
![]()
Плечо откладываем перпендикулярно линии действия силы, причём перпендикуляр опускаем из центра масс звена, и из полученной точки проводим линию, параллельно направлению действия силы инерции. Пересечение этой линии со звеном (действительное или мнимое) даёт нам точку приложения соответствующей силы инерции.
2.2 Расчёт диады 4-5
Для расчёта
этой диады изобразим её со всеми приложенными к ней силами. Действия
отброшенных связей заменяем реакциями ![]() и
и ![]() . Из условия равновесия ползуна 4
получим:
. Из условия равновесия ползуна 4
получим: ![]() .
Составим уравнение равновесия ползуна 5:
.
Составим уравнение равновесия ползуна 5:
![]()
Строим план сил для диады 4-5. Масштабный коэффициент плана сил.
![]()
Из плана сил получаем
![]()
![]()
![]()
![]()
2.3 Расчёт диады 2-3
Изобразим
диаду со всеми приложенными к ней силами. В точках А и О2 взамен отброшенных
связей прикладываем реакции ![]() и
и ![]() . В точке С прикладываем ранее
найденную реакцию
. В точке С прикладываем ранее
найденную реакцию ![]() . Реакции
. Реакции ![]() и
и ![]() разложим на нормальные и
касательные составляющие, при этом касательную составляющую
разложим на нормальные и
касательные составляющие, при этом касательную составляющую ![]() найдём по уравнению
равновесия моментов сил, приложенных к звену 2:
найдём по уравнению
равновесия моментов сил, приложенных к звену 2:
![]() , откуда
, откуда
![]()
Касательную составляющую ![]() найдём,
составив и решив уравнение равновесия моментов сил, приложенных к звену 3:
найдём,
составив и решив уравнение равновесия моментов сил, приложенных к звену 3:
![]() , откуда
, откуда
![]()
Строим план сил, предварительно рассчитав отрезки в мм:
![]()
![]()
![]()
![]()
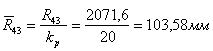
![]()
![]()
![]()
![]()
![]()
Реакцию внутреннюю в точке B определим на основании уравнения равновесия звена 2:
![]()
![]()
2.4 Расчёт кривошипа
Изобразим
кривошип с приложенными к нему силами и уравновешивающей силой Ру, эквивалентной
силе действия на кривошип со стороны двигателя. Действие отброшенных связей
учитываем, вводя реакции ![]() и
и ![]() . Определяем уравновешивающую
силу, считая, что она приложена в точке А кривошипа, перпендикулярно ему.
Уравнение равновесия кривошипа в этом случае принимает вид:
. Определяем уравновешивающую
силу, считая, что она приложена в точке А кривошипа, перпендикулярно ему.
Уравнение равновесия кривошипа в этом случае принимает вид:
![]()
откуда находим
![]()
![]()
2.5 Определение уравновешивающей силы методом Жуковского
Строим повёрнутый на 90° план скоростей и в соответствующих точках прикладываем все внешние силы, включая Ру и силы инерции. Составим уравнение моментов относительно точки РV, считая силу Ру неизвестной:
![]()
![]()
![]()
Погрешность графического метода
![]()
2.6 Определение мощностей
Мгновенная потребляемая мощность без учета потерь на трение:
![]()
Мощность привода на трение на преодоление силы полезного сопротивления:
![]() ,
,
где f- коэффициент трения, R-реакция во вращательной паре, rц – радиус цапф.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Суммарная мощность трения
![]()
Мгновенная потребляемая мощность
![]()
2.7 Определение кинематической энергии механизма
Кинематическая энергия механизма равна суммарной кинематической энергии входящих в него массивных звеньев.
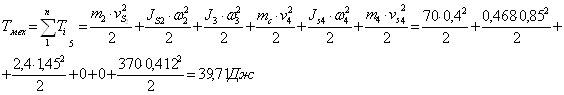
За звено приведения выбираем кривошип. Кинетическая энергия кривошипа равна:
![]()
![]()
![]()
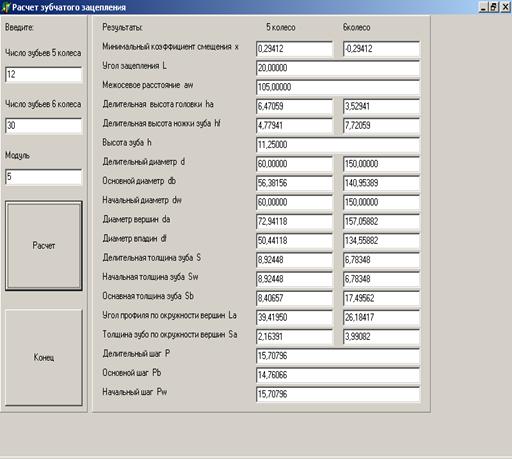
3. Геометрический расчет зубчатой передачи. Проектирование
планетарного редуктора
3.1 Геометрический расчёт зубчатой передачи
Исходные данные:
- число зубьев шестерни Z512
- число зубьев колеса Z630
- модуль зубчатых колёс m, мм5
Нарезание зубчатых колёс производится методом обкатки инструментом реечного типа, имеющего следующие параметры:
- коэффициент высоты головки зуба ![]()
![]() 1
1
- коэффициент радиального зазора ![]() 0,25
0,25
- угол профиля α, град20
Суммарное число зубьев колёс
![]()
Поскольку ![]() , то проектируем равносмещённое
зубчатое зацепление.
, то проектируем равносмещённое
зубчатое зацепление.
Минимальный коэффициент смещения шестерни и колеса
![]()
![]()
Делительное межосевое расстояние
![]()
Делительная высота головки зуба
![]()
![]()
Делительная высота ножки зуба
![]()
![]()
Высота зуба
![]()
Делительный диаметр
![]()
![]()
Основной диаметр
![]()
![]()
Диаметр вершин зубьев
![]()
![]()
Диаметр впадин зубьев
![]()
![]()
Делительная толщина зуба
![]()
![]()
Основная толщина зуба
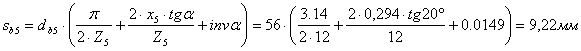
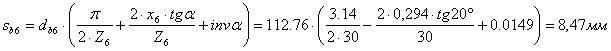
Угол профиля по окружности вершин
![]()
![]()
Толщина зуба по окружности вершин
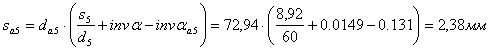
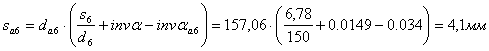
Делительный шаг
![]()
Основной шаг
![]()
Строим картину эвольвентного
зацепления по результатам расчетов. Масштабный коэффициент построения ![]() .
.
Определение коэффициента торцового перекрытия аналитически
![]()
Текст расчетной программы
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Buttons;
type
TForm1 = class(TForm)
GroupBox1: TGroupBox;
Edit1: TEdit; Edit2: TEdit; Edit3: TEdit; Edit4: TEdit; Edit5: TEdit;
Edit6: TEdit; Label1: TLabel; Label2: TLabel; Label3: TLabel;
Label4: TLabel; Label5: TLabel; Label6: TLabel; GroupBox2: TGroupBox;
Edit7: TEdit; Edit8: TEdit; Edit9: TEdit; Edit10: TEdit; Edit11: TEdit;
Edit12: TEdit; Edit13: TEdit; Edit14: TEdit; Edit15: TEdit; Edit16: TEdit;
Edit17: TEdit; Edit18: TEdit; Edit19: TEdit; Edit20: TEdit; Edit21: TEdit;
Edit22: TEdit; Edit23: TEdit; Edit24: TEdit; Edit25: TEdit; Edit26: TEdit;
Edit27: TEdit; Label7: TLabel; Label8: TLabel; Label9: TLabel;
Label10: TLabel; Label11: TLabel; Label12: TLabel; Label13: TLabel;
Label14: TLabel; Label15: TLabel; Label16: TLabel; Label17: TLabel;
Label18: TLabel; Label19: TLabel; Label20: TLabel; Label21: TLabel;
Label22: TLabel; Label23: TLabel; Label24: TLabel; Label25: TLabel;
Label26: TLabel; Label27: TLabel; BitBtn1: TBitBtn; BitBtn2: TBitBtn;
procedure BitBtn1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
Z1,Z2,X1,X2,Aw,A,q,h,ha,ha1,c,ha2,m,hf1,hf2,d1,d2,dw1,dw2,db1,db2,da1,da2,
df1,df2,S1,S2,P,Pb,r:real;
implementation
{$R *.dfm}
procedure TForm1.BitBtn1Click(Sender: TObject);
begin
Z1:=strtoFloat(Edit1.Text);
Z2:=strtoFloat(Edit2.Text);
m:=strtoFloat(Edit3.Text);
ha:=strtoFloat(Edit4.Text);
c:=strtoFloat(Edit5.Text);
q:=strtoFloat(Edit6.Text);
q:=q*pi/180;
X1:=( 17-Z1)/17;
X2:=-X1;
A:=0.5*m*(Z1+Z2);
Aw:=A;
h:=2.25*m;
ha1:=m*(ha+X1);
ha2:=m*(ha+X2);
hf1:=m*(ha+c-X1);
hf2:=m*(ha+c-X2);
d1:=m*Z1;
d2:=m*Z2;
dw1:=d1;
dw2:=d2;
db1:=d1*cos(q);
db2:=d2*cos(q);
da1:=d1+2*ha1;
da2:=d2+2*ha2;
df1:=d1-2*hf1;
df2:= d2-2*hf2;
S1:=0.5*Pi*m+2*m*X1*sin(q)/cos(q);
S2:=0.5*Pi*m+2*m*X2*sin(q)/cos(q);
P:=Pi*m;
Pb:=P*cos(q);
r:=0.38*m;
Edit7.Text:=FloatToStr(X1);
Edit8.Text:=FloatToStr(X2);
Edit9.Text:=FloatToStr(a);
Edit10.Text:=FloatToStr(h);
Edit11.Text:=FloatToStr(ha1);
Edit12.Text:=FloatToStr(ha2);
Edit13.Text:=FloatToStr(d1);
Edit14.Text:=FloatToStr(d2);
Edit15.Text:=FloatToStr(dw1);
Edit16.Text:=FloatToStr(dw2);
Edit17.Text:=FloatToStr(db1);
Edit18.Text:=FloatToStr(db2);
Edit19.Text:=FloatToStr(da1);
Edit20.Text:=FloatToStr(da2);
Edit21.Text:=FloatToStr(df1);
Edit22.Text:=FloatToStr(df2);
Edit23.Text:=FloatToStr(S1);
Edit24.Text:=FloatToStr(S2);
Edit25.Text:=FloatToStr(P);
Edit26.Text:=FloatToStr(Pb);
Edit27.Text:=FloatToStr(r);
end;
end.
Вид приложения
3.2 Проектирование планетарного редуктора
Исходные данные:
Модуль ![]()
Частота
вращения вала двигателя ![]()
Частота
вращения кривошипа ![]()
Числа зубьев ![]()
Знак передаточного отношения – минус
Номер схемы
редуктора ![]()

1. Передаточное отношение простой передачи
![]()
2. Общее передаточное отношение редуктора
![]()
3. Передаточное отношение планетарной передачи
![]()
4. Формула Виллиса для планетарной передачи
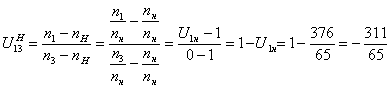
5. Передаточное отношение обращенного механизма, выраженное в числах зубьев.
![]()
6. Подбор чисел зубьев
Принимаем:
![]() тогда
тогда ![]()
![]()
Получаем ![]()
7. Условие соосности
![]() или
или ![]()
Условие соосности выполнено
8. Делительные диаметры
![]()
![]()
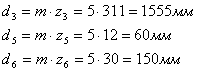
9. Линейная скорость точки A колеса z1
![]()
10. Масштабный коэффициент Kv
![]()
11. Масштабный коэффициент построения плана частот вращения редуктора
![]()
3.3 Определение частот вращения аналитическим методом
![]() ; откуда
; откуда ![]() .
.
![]() ;
; ![]() ;
; ![]() ;
; ![]()
3.4 Определение частот вращения графическим методом
Масштабный коэффициент плана частот вращений:
![]() .
.
Частоты вращения, полученные графическим способом:
![]()
![]()
![]()
4. Синтез и анализ кулачкового механизма
Исходные данные:
- № кинематического графика движения толкателя4
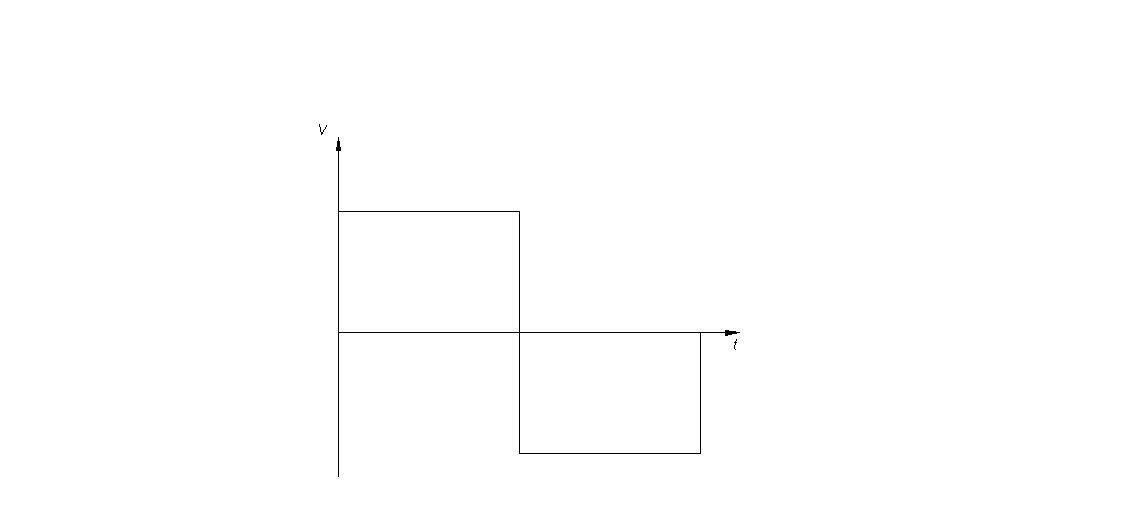 - тип толкателя – плоский толкатель
- тип толкателя – плоский толкатель
- максимальный ход (подъем) толкателя h, мм 50
- рабочий
угол кулачка ![]() , град200
, град200
- частота вращения кривошипа nкр, мин-165
Рисунок 5 – Диаграмма движения выходного звена
4.1 Построение диаграмм и определение масштабных
коэффициентов
По заданному графику скорости толкателя графическим интегрированием по методу хорд строят 2 графика – график ускорения толкателя a(t) и график перемещения толкателя S(t). Базы интегрирования Н1=60мм.
Определяем масштабные коэффициенты:
Масштабный коэффициент перемещения
![]()
где h – максимальный ход толкателя, м;
yh – максимальная ордината графика соответствующая заданному подъёму толкателя, мм.
Масштабный коэффициент времени
![]()
где φр – рабочий угол кулачка, град;
nкул – частота вращения кулачка, мин-1;
xt – длина отрезка на оси абсцисс графика, изображающая время поворота кулачка на рабочий угол, мм.
Масштабный коэффициент скорости толкателя
![]()
4.2 Минимальный радиус кулачка
Выбираем исходя из условия R0≥h
R0=150 мм
4.3 Построение профиля кулачка
Профиль
кулачка строим в масштабном коэффициенте построения ![]() Проводим окружность радиусом R0, откладываем фазовый
рабочий угол
Проводим окружность радиусом R0, откладываем фазовый
рабочий угол ![]() ْ и делим его на 12 частей.
От точки деления проводим ось. Вдоль оси толкателя откладываем текущее
перемещение толкателя от окружности минимального радиуса и проводим
перпендикуляры к линиям. Профилем кулачка будет огибающая всех положений
тарелки толкателя.
ْ и делим его на 12 частей.
От точки деления проводим ось. Вдоль оси толкателя откладываем текущее
перемещение толкателя от окружности минимального радиуса и проводим
перпендикуляры к линиям. Профилем кулачка будет огибающая всех положений
тарелки толкателя.
4.4 Определение максимальной скорости и ускорения толкателя
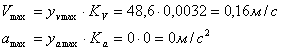
где ![]() ,
, ![]() – максимальные
ординаты скорости и ускорения на соответствующих графиках, мм.
– максимальные
ординаты скорости и ускорения на соответствующих графиках, мм.
Составляем программу определения профиля кулачка.
Public Sub kulachok()
Dim I As Integer
Dim dis1, dis2, R, a1, a2, arksin1, arksin2, BETTA As Single
Dim R0, FIR, FI0, FII, SHAG, E As Single
Dim S(1 To 10) As Single
Worksheets(1).Activate
Worksheets(1).Range("a:o").Clear
Worksheets(1).ChartObjects.Delete
R0 = InputBox("ВВЕДИТЕ МИНИМАЛЬНЫЙ РАДИУС КУЛАЧКА RO")
FIR = InputBox("ВВЕДИТЕ РАБОЧИЙ УГОЛ КУЛАЧКА FIR")
FI0 = InputBox("ВВЕДИТЕ НАЧАЛЬНОЕ ЗНАЧЕНИЕ УГЛА_
ПОВОРОТА КУЛАЧКА FI0")
E = InputBox("ВВЕДИТЕ ДЕЗАКСИАЛ E")
For I = 1 To 10
S(I) = InputBox("ВВЕДИТЕ СТРОКУ ПЕРЕМЕЩЕНИЙ S(" & I & ")")
Next I
FIR = FIR * 0.0174532
SHAG = FIR / 10
FI0 = FI0 * 0.0174532
FII = FI0
For I = 1 To 10
dis1 = (R0 ^ 2 - E ^ 2) ^ (1 / 2)
dis2 = S(I) ^ 2 + R0 ^ 2 + 2 * S(I) * dis1
R = dis2 ^ (1 / 2)
a1 = E / R
a2 = E / R0
arksin1 = Atn(a1 / (1 - a1 ^ 2) ^ (1 / 2))
arksin2 = Atn(a1 / (1 - a2 ^ 2) ^ (1 / 2))
BETTA = FII + arksin1 - arksin2
BETTA = BETTA * 180 / 3.1415
Worksheets(1).Cells(1, 1) = "R"
Worksheets(1).Cells(1, 2) = "BETTA"
Worksheets(1).Cells(I + 1, 1) = R
Worksheets(1).Cells(I + 1, 2) = BETTA
FII = FII + SHAG
Next I
End Sub
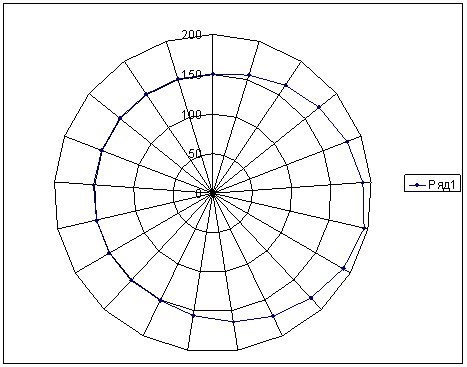
Результаты работы программы
| R, мм | BETTA |
| 150 | 0 |
| 155,35 | 16,67 |
| 164,33 | 33,34 |
| 172,64 | 50,01 |
| 180,96 | 66,68 |
| 189,98 | 83,35 |
| 195,04 | 100,02 |
| 189,98 | 116,69 |
| 180,96 | 133,36 |
| 172,64 | 150,03 |
| 164,33 | 166,70 |
| 155,35 | 183,37 |
| 150 | 200,04 |
| 150 | 216,71 |
| 150 | 233,38 |
| 150 | 250,05 |
| 150 | 266,72 |
| 150 | 283,39 |
| 150 | 300,06 |
| 150 | 316,73 |
| 150 | 333,40 |
| 150 | 350,07 |
| 150 | 360,00 |
Список литературы
1. Артоболевский И.И. Теория машин и механизмов.–Наука, М.: 1998 – 720 с.
2. Кожевников С.Н., Теория машин и механизмов, Машиностроение, М.: 1969г. – 538 с.
3. Корняко А.С., Курсовое проектирование по теории машин и механизмов. – Вища школа, Киев: 1970г. – 330 с.
4. Фролов И.П., Теория механизмов, машин и манипуляторов. – Дизайн ПРО, Минск .: 1998 г. – 428 с.
5. Фролов К.В., Теория механизмов и машин. Высшая школа, М.: 1998 – 494с.