Курсовая работа: Проектирование электродвигателя асинхронного с короткозамкнутым ротором мощностью 37 кВт
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
курсовой проект
по дисциплине: «Электрические машины»
на тему: «ПРОЕКТИРОВАНИЕ ЭЛЕКТРОДВИГАТЕЛЯ АСИНХРОННОГО С КОРОТКОЗАМКНУТЫМ РОТОРОМ МОЩНОСТЬЮ 37 кВт»
Содержание
Введение
1. Расчет и конструирование двигателя
1.1 Выбор главных размеров
1.2 Расчет обмотки статора
1.3 Расчет размеров зубцовой зоны статора и воздушного зазора
1.4 Расчет ротора
1.5 Расчет магнитной цепи
1.6 Расчет параметров рабочего режима
1.7 Расчет потерь
1.8 Расчет рабочих характеристик
1.9 Расчет пусковых характеристик
1.10 Тепловой и вентиляционный расчет
1.11 Механический расчет
2. Моделирование двигателя
3. Исследовательская часть
4. Выбор схемы управления двигателем
Заключение
Список литературы
Введение
Значение электрической энергии в народном хозяйстве и в быту непрерывно возрастает.
Промышленность, транспорт, сельское хозяйство и быт населения обусловливает необходимость применения разнообразного электротехнического оборудования.
Основой автоматизированного электропривода являются электрические двигатели. По мере развития силовой полупроводниковой техники и микропроцессорных систем управления двигатели постоянного тока в замкнутых системах электропривода постепенно вытесняются более надежными и дешевыми асинхронными двигателями с короткозамкнутым ротором.
Двигатели серии 4А выпускались в 80-х годах в массовом количестве и в настоящее время эксплуатируются практически на всех промышленных предприятиях. Серия охватывает диапазон мощностей от 0,6 до 400 кВт и построена на 17 стандартных высотах вращения от 50 до 355 мм. Серия включает основное исполнение двигателей, ряд модификаций и специализированное исполнение.
В данной курсовой работе будет произведено проектирование асинхронного двигателя, номинальные данные которого и указания о режиме его работы приведены в техническом задании. Проектирование новой машины начинаем с выбора базовой модели, на которую ориентируемся при проведении всех расчётов, начиная с выбора главных размеров, и при разработке конструкций отдельных узлов. За базовую выберем конструкцию двигателя серии 4А – 4А200М2У3, основные технические данные которого сведены в таблицу:
|
|
|
|
|
|
|
|
|
|||||||||
| 37 | 0,82 | 40,3 | 4,3 | 90 | 0,89 | 1,4 | 2,5 | |||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
| 4,1 | 0,028 | 0,094 | 0,021 | 0,12 | 0,031 | 0,060 | 0,16 | 1,9 | 11,5 | |||||||
Полностью учесть все требования технического задания к характеристикам двигателя, не ориентируясь на данные выпущенных машин, невозможно. Поэтому перед началом расчёта детально изучим конструкцию базового двигателя.
1. Расчет и конструирование двигателя
1.1 Выбор главных размеров
По табл. 8.6 [1, c.275] принимаем внешний диаметр
статора ![]() .
.
При определении
внутреннего диаметра статора ![]() ,
принимая, что размеры пазов не зависят от числа полюсов машины, получаем
приближенное выражение:
,
принимая, что размеры пазов не зависят от числа полюсов машины, получаем
приближенное выражение:
|
|
|
где ![]() – коэффициент,
характеризующий отношение внутренних и внешних диаметров сердечников статоров
асинхронных двигателей.
– коэффициент,
характеризующий отношение внутренних и внешних диаметров сердечников статоров
асинхронных двигателей.
По табл. 8.7 [1, c.276] принимаем ![]() .
.
Внутренний диаметр
статора ![]() .
.
Находим полюсное деление по формуле:
|
|
|
где ![]() – число пар полюсов.
– число пар полюсов.
![]() .
.
Определяем расчётную мощность по формуле:
|
|
|
где ![]() – мощность на валу
двигателя, кВт;
– мощность на валу
двигателя, кВт;
![]() – отношение ЭДС обмотки статора к
номинальному напряжению, значение которого принимаем по рис. 8.20 [1,
с,276].
– отношение ЭДС обмотки статора к
номинальному напряжению, значение которого принимаем по рис. 8.20 [1,
с,276].
Предварительные значения ![]() и
и ![]() находятся по ГОСТ.
Приближенные значения
находятся по ГОСТ.
Приближенные значения ![]() и
и ![]() определяем по кривым рис.
8.21 [1, с,277].
определяем по кривым рис.
8.21 [1, с,277].
![]()
Определяем электромагнитные нагрузки (предварительно по рис. 8.22 [1, с,278]):
![]() ;
; ![]() .
.
Обмоточный коэффициент
для двухслойной обмотки при ![]() принимаем
принимаем
![]() .
.
Определяем расчетную длину магнитопровода по формуле:
|
|
|
где ![]() – синхронная угловая
скорость двигателя,
– синхронная угловая
скорость двигателя, ![]() ;
;
![]() – коэффициент формы поля.
– коэффициент формы поля.
![]() .
.
Критерием правильности
выбора ![]() и
и ![]() служит отношение
служит отношение ![]() , которое в данном случае
находится в допустимых пределах, показанных на рис. 8.25 [1, с,280].
, которое в данном случае
находится в допустимых пределах, показанных на рис. 8.25 [1, с,280].
На этом выбор главных размеров заканчивается.
Выполняем сравнение параметров проектируемого АД, полученных в данном разделе, с теми же параметрами аналога:
|
Величина |
|
|
|
|
Проектируемый АД |
|
|
|
|
Аналог |
|
|
|
1.2 Расчет обмотки статора
Принимаем зубцовое
деление ![]() по рис. 8.26 [1,
с.282].
по рис. 8.26 [1,
с.282].
Предельные значения ![]() :
: ![]() ;
; ![]()
Тогда возможность числа
пазов статора, соответствующих выбранному диапазону ![]() ,
,
|
|
|
Тогда
![]()
![]()
Окончательно число пазов
статора из выбранного диапазона![]() , тогда
, тогда ![]() . Обмотка двухслойная.
. Обмотка двухслойная.
Зубцовое деление статора (окончательно):
![]() .
.
Число эффективных
проводников в пазу (при условии наличия параллельных ветвей ![]() ):
):
|
|
|
где ![]() – принятое ранее значение
линейной нагрузки,
– принятое ранее значение
линейной нагрузки, ![]() ;
;
![]() – номинальный ток обмотки статора, А.
– номинальный ток обмотки статора, А.
|
|
|
Тогда
![]() .
.
![]() .
.
Принимаем ![]() , тогда по 8.19 [1,
с.284]
, тогда по 8.19 [1,
с.284] ![]() проводников.
проводников.
Полученное число ![]() округляем до четного
целого:
округляем до четного
целого: ![]() .
.
Окончательное число витков в фазе обмотки:
|
|
|
Имеем
![]() .
.
Окончательное значение
линейной нагрузки, ![]() :
:
|
|
|
Получим
![]() .
.
Далее определяем
обмоточный коэффициент исходя из того, что общим аналитическим выражением для
расчета ![]() большинства современных
симметричных обмоток с фазной зоной, равной электрическому углу
большинства современных
симметричных обмоток с фазной зоной, равной электрическому углу ![]() радиан, и с целым числом
пазов на полюс и фазу является:
радиан, и с целым числом
пазов на полюс и фазу является:
|
|
|
где ![]() – номер гармоники ЭДС
(для основной гармоники
– номер гармоники ЭДС
(для основной гармоники ![]() );
);
![]() – число пазов на полюс и фазу;
– число пазов на полюс и фазу;
![]() – относительный шаг обмотки, в
двухслойных обмотках асинхронных двигателей выполняют с укорочением, близким к
– относительный шаг обмотки, в
двухслойных обмотках асинхронных двигателей выполняют с укорочением, близким к ![]() .
.
Поэтому
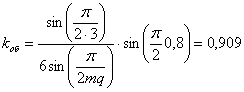 .
.
После расчета ![]() уточняем значение потока
уточняем значение потока ![]() :
:
|
|
|
Тогда
![]() .
.
Определяем индукцию в воздушном зазоре:
|
|
|
Имеем
![]() .
.
Значения ![]() и
и ![]() находятся в допустимых
пределах (см. рис.8.22, б [1, c.278]).
находятся в допустимых
пределах (см. рис.8.22, б [1, c.278]).
Плотность тока в обмотке статора:
|
|
|
где ![]() – по рис. 8.27 [1, c.286].
– по рис. 8.27 [1, c.286].
![]() .
.
Площадь поперечного сечения эффективных проводников, определяют, исходя из тока одной параллельной ветви и допустимой плотности тока в обмотке:
|
|
|
![]() .
.
Сечение эффективного проводника (окончательно):
принимаем число
элементарных проводников ![]() , тогда
, тогда ![]() .
.
Принимаем обмоточный провод марки ПЭТМ (см. приложение 3 [1]):
![]() ;
;
![]() ;
;
![]() .
.
Тогда ![]() .
.
Плотность тока в обмотке статора:
|
|
|
Окончательно
![]() .
.
Выполняем равнение параметров проектируемого АД, полученных в данном разделе, с теми же параметрами аналога:
|
Величина |
|
|
|
|
|
|
|
|
|
Проектируемый АД |
36 |
|
40,16 | 0,814 | 4 | 1,18 | 1,24 | 4,629 |
|
Аналог |
36 |
|
40,3 | 0,82 | 4 | 1,5 | 1,58 | 4,3 |
1.3 Расчет размеров зубцовой зоны статора и воздушного зазора
Паз статора рассчитываем в соответствии с рис.1 с соотношением размеров, обеспечивающих параллельность боковых граней зубцов.
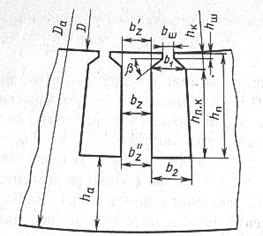
Рис. 1 - Трапецеидальные пазы статора
Принимаем предварительно
по табл. 8.10 [1, с.289]: ![]() ;
; ![]() , тогда
, тогда
|
|
|
где ![]() – коэффициент заполнения
сердечника сталью, по табл. 8.11 [1, с.290].
– коэффициент заполнения
сердечника сталью, по табл. 8.11 [1, с.290].
![]() .
.
По выбранным значениям индукций определяем высоту ярма статора:
|
|
|
![]()
Принимаем размеры паза в штампе:
ширина шлица паза – ![]() ;
;
высота шлица паза – ![]() .
.
Принимаем угол наклона
грани клиновой части в трапецеидальных пазах с ![]()
![]() [1, с.294].
[1, с.294].
Высоту паза определяем по формуле:
|
|
|
Получим: ![]() .
.
Размер ![]() определяют в зависимости
от угла
определяют в зависимости
от угла ![]() :
:
|
|
|
![]() .
.
|
|
|
![]() .
.
|
|
|
![]()
Сумма размеров по высоте и ширине паза всех проводников и изоляции с учетом необходимых допусков на разбухание изоляции и на укладку обмотки определяет размеры части паза, занятой обмоткой.
Полученные при расчете заполнения паза его размеры являются размерами паза “в свету”, т.е размерами реального паза в собранном шихтованном сердечнике с учетом неизбежной при этом “гребенки”, образующейся за счет допусков при штамповке листов и шихтовке магнитопроводов.
Размеры паза “в свету” будут меньше, чем в штампе, т.е чем размеры паза в каждом отдельном листе штамповки, на величину припусков:
по ширине паза ![]() ;
;
по высоте паза ![]() .
.
Размеры паза “в свету” с учетом припуска на сборку:
|
|
|
где ![]() ,
, ![]() и
и ![]() – размеры паза “в свету”,
полученные при расчете заполнения паза проводниками обмотки изоляцией.
– размеры паза “в свету”,
полученные при расчете заполнения паза проводниками обмотки изоляцией.
Тогда
![]() ;
;
![]() ;
;
![]() .
.
Площадь поперечного сечения трапецеидального паза, в которой размещаются обмотка, корпусная изоляция и прокладки:
|
|
|
где ![]() – площадь поперечного
сечения корпусной изоляции в пазу,
– площадь поперечного
сечения корпусной изоляции в пазу, ![]() ;
;
![]() – площадь, занимаемая прокладками в
пазу (на дне паза, под клином и между слоями в двухслойной обмотке):
– площадь, занимаемая прокладками в
пазу (на дне паза, под клином и между слоями в двухслойной обмотке):
|
|
|
Площадь поперечного сечения корпусной изоляции в пазу находим по формуле:
|
|
|
где ![]() – односторонняя толщина
изоляции в пазу по табл. 3.1 [1, с.74].
– односторонняя толщина
изоляции в пазу по табл. 3.1 [1, с.74].
Получим
![]() .
.
![]() .
.
Тогда
![]() .
.
Контролем правильности размещения обмотки в пазах является значение коэффициента заполнения паза:
|
|
|
Окончательно
![]() .
.
Полученное значение ![]() допустимо для механизированной
укладки обмотки.
допустимо для механизированной
укладки обмотки.
Выполняем сравнение параметров проектируемого АД, полученных в данном разделе, с теми же параметрами аналога:
|
Величина |
|
|
|
|
Проектируемый АД |
9,009 | 14,243 | 29,984 |
|
Аналог |
10,5 | 14,9 | 28,2 |
1.4 Расчет ротора
Определяем воздушный зазор по формуле:
|
|
|
Имеем
![]() .
.
По рис. 8.31 [1,
с.300] принимаем ![]() .
.
Число пазов ротора по табл.
8.16 [1, с.306]: ![]() .
.
Внешний диаметр ротора: ![]() .
.
Длина магнитопровода
ротора: ![]() .
.
Зубцовое деление ротора:
|
|
|
Тогда
![]() .
.
Внутренний диаметр ротора равен диаметру вала, так как сердечник ротора непосредственно насаживается на вал:
|
|
|
где ![]() – коэффициент по табл.
8.17 [1, с.319].
– коэффициент по табл.
8.17 [1, с.319].
![]() .
.
Ток в обмотке ротора:
|
|
|
где ![]() – коэффициент, учитывающий
влияние тока намагничивания на отношение
– коэффициент, учитывающий
влияние тока намагничивания на отношение ![]() ;
;
![]() – коэффициент приведения токов.
– коэффициент приведения токов.
Приближенное значение ![]() может быть рассчитано в
зависимости от номинального
может быть рассчитано в
зависимости от номинального ![]() ,
который был определен в начале расчета:
,
который был определен в начале расчета:
|
|
|
Получим
![]() ;
;
Коэффициент приведения токов определяем следующим образом:
|
|
|
где ![]() – коэффициент, учитывающий
влияние скоса пазов, так как пазы ротора выполняем без скоса, то
– коэффициент, учитывающий
влияние скоса пазов, так как пазы ротора выполняем без скоса, то ![]() .
.
Тогда
![]() ;
;
![]() .
.
Площадь поперечного сечения стержня:
|
|
где ![]() – плотность тока в стержне
литой клетки,
– плотность тока в стержне
литой клетки, ![]() .
.
Получим
![]() .
.
Пазы ротора представлены на рис.2.
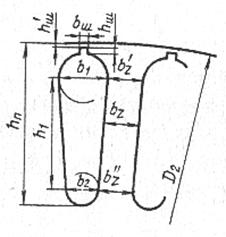
Рис.2 - Грушевидные пазы короткозамкнутого ротора
Принимаем по [1, с.313] ![]() ,
, ![]() ,
, ![]() .
.
По табл. 8.10 [1,
с.289] принимаем допустимое значении индукции на зубцах ротора ![]() .
.
По допустимой индукции определяем ширину зубца ротора:
|
|
|
Получим
![]() .
.
После чего рассчитываем размеры паза:
|
|
|
|
|
|
|
|
|
Тогда
![]() ;
;
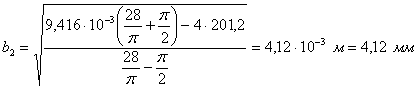 .
.
Условия
высококачественной заливки пазов алюминием требуют, чтобы диаметр закругления
нижней части паза в двигателях с ![]() – не
менее 2,5 – 3 мм.
– не
менее 2,5 – 3 мм.
В связи с округлениями
результатов расчета необходимо просчитать ширину зубцов в сечениях ![]() и
и ![]() по окончательно принятым
размерам паза:
по окончательно принятым
размерам паза:
|
|
|
|
|
|
Имеем
![]() ;
;
![]() ;
;
По рис.2. принимаем ![]() ,
, ![]() ,
, ![]() .
.
Полная высота паза:
|
|
|
Тогда
![]() .
.
Площадь поперечного сечения стержня:
|
|
|
Получим
![]()
Плотность тока в стержне:
|
|
|
Имеем
![]() .
.
Площадь поперечного сечения замыкающих колец:
|
|
|
где ![]() – токи в кольце, А;
– токи в кольце, А;
![]() – плотность тока в замыкающих
кольцах.
– плотность тока в замыкающих
кольцах.
Токи в кольце и плотность тока можно найти по формулам соответственно:
|
|
|
|
|
|
где ![]() – токи в стержнях;
– токи в стержнях;
![]() .
.
Тогда
![]() ;
;
![]()
Размеры замыкающих колец:
![]() ;
;
![]() ;
;
![]() ;
;
средний диаметр замыкающих колец:
![]() .
.
Разрез зубца и паза статора представлен на рис.5.
Сравнение параметров проектируемого АД, полученных в данном разделе, с теми же параметрами аналога:
| Величина |
|
|
|
|
|
| Проектируемый АД | 0,9 | 28 | 32,57 | 9,416 | 4,12 |
| Аналог | 0,9 | 28 | 34,4 | 6,9 | 5,6 |
1.5 Расчет магнитной цепи
Марку электротехнической стали выбираем по рекомендациям [1, с320] в зависимости от оси вращения проектируемого асинхронного двигателя – сталь 2212, с толщиной листов 0,5 мм.
Магнитное напряжение воздушного зазора
|
|
|
где ![]() – индукция в воздушном
зазоре, Тл, рассчитанная по ф. по окончательно принятому числу витков в
фазе обмотки
– индукция в воздушном
зазоре, Тл, рассчитанная по ф. по окончательно принятому числу витков в
фазе обмотки ![]() и обмоточному коэффициенту
и обмоточному коэффициенту
![]() , определенному для принятой
в машине обмотки;
, определенному для принятой
в машине обмотки;
![]() – воздушный зазор, м;
– воздушный зазор, м;
![]() – коэффициент воздушного зазора;
– коэффициент воздушного зазора;
![]() – магнитная проницаемость,
– магнитная проницаемость, ![]() .
.
Коэффициент воздушного зазора:
|
|
|
|
|
|
Имеем
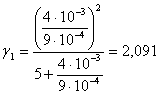 ;
; ![]() ,
,
следовательно ![]() .
.
Магнитное напряжение зубцовой зоны статора:
|
|
|
где ![]() – расчетная высота зубца
статора, м;
– расчетная высота зубца
статора, м;
![]() – расчетная напряженность поля в
зубце статора, А, принимаем по приложению 1 [1], при условии, что
– расчетная напряженность поля в
зубце статора, А, принимаем по приложению 1 [1], при условии, что ![]() .
.
Поэтому
![]() .
.
Расчетная индукция в зубцах:
|
|
|
Тогда
![]() .
.
Магнитное напряжение зубцовой зоны ротора:
|
|
|
где ![]() – расчетная высота зубца
ротора, м;
– расчетная высота зубца
ротора, м;
![]() – расчетная напряженность поля в
зубце ротора, А, принимаем по приложению 1 [1], при условии, что
– расчетная напряженность поля в
зубце ротора, А, принимаем по приложению 1 [1], при условии, что ![]() .
.
Получим
![]() .
.
При зубцах на рис.2 из табл. 8.18 [1, c324]:
|
|
|
Тогда
![]()
Индукция в зубце:
|
|
|
Имеем
![]() .
.
По табл. П.10 [2,
с331] для ![]() находим
находим ![]() .
.
Коэффициент насыщения зубцовой зоны:
|
|
|
Тогда
![]()
Магнитное напряжение ярма статора:
|
|
|
где ![]() – длина средней магнитной
силовой линии в ярме статора, м;
– длина средней магнитной
силовой линии в ярме статора, м;
![]() – напряженность поля при индукции
– напряженность поля при индукции ![]() по кривой намагничивания
для ярма, принятой при проектировании стали, по приложению П.9. [1].
по кривой намагничивания
для ярма, принятой при проектировании стали, по приложению П.9. [1].
Длина средней магнитной силовой линии в ярме статора:
|
|
|
где ![]() – высота ярма статора, м:
– высота ярма статора, м:
|
|
|
Окончательно
![]() ;
;
![]() ;
;
![]() .
.
Индукция в ярме статора:
|
|
|
где ![]() – расчетная высота ярма
статора, м; при отсутствии радиальных вентиляционных каналов в статоре
– расчетная высота ярма
статора, м; при отсутствии радиальных вентиляционных каналов в статоре ![]() .
.
Для ![]() по табл. П.9 [2,
с331] находим
по табл. П.9 [2,
с331] находим ![]() .
.
Магнитное напряжение ярма ротора:
|
|
|
где ![]() – напряженность поля в
ярме при индукции
– напряженность поля в
ярме при индукции ![]() по кривой
намагничивания для ярма принятой при проектировании стали.
по кривой
намагничивания для ярма принятой при проектировании стали.
![]() – длина силовых линий в ярме, м:
– длина силовых линий в ярме, м:
|
|
|
Получим
![]() .
.
Индукция в ярме ротора:
|
|
|
где ![]() – коэффициент заполнения
сталью ярма ротора,
– коэффициент заполнения
сталью ярма ротора, ![]() принят ранее;
принят ранее;
![]() – расчетная высота ярма ротора, м:
– расчетная высота ярма ротора, м:
|
|
|
Тогда
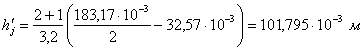 ;
;
![]() .
.
Для ![]() по табл. П.9 [2,
с331] находим
по табл. П.9 [2,
с331] находим ![]() .
.
Тогда
![]() .
.
На этом расчет магнитных напряжений участков магнитной цепи двигателя заканчивается. Суммарное магнитное напряжение магнитной цепи на пару полюсов:
|
|
|
Получим
![]() .
.
Коэффициент насыщения магнитной цепи:
|
|
|
Тогда
![]() .
.
Намагничивающий ток:
|
|
|
Окончательно
![]()
Относительное значение по 8.129 [1, с.330]:
![]() , поэтому можно сделать вывод о том, что размеры
машины выбраны правильно.
, поэтому можно сделать вывод о том, что размеры
машины выбраны правильно.
1.6 Расчет параметров рабочего режима
Активное сопротивление обмотки статора:
|
|
|
где ![]() – коэффициент увеличения
активного сопротивления фазы обмотки от действия эффекта вытеснения тока (в
проводниках обмотки статора асинхронных машин эффект вытеснения тока
проявляется незначительно из-за малых размеров элементарных проводников,
поэтому
– коэффициент увеличения
активного сопротивления фазы обмотки от действия эффекта вытеснения тока (в
проводниках обмотки статора асинхронных машин эффект вытеснения тока
проявляется незначительно из-за малых размеров элементарных проводников,
поэтому ![]() );
);
![]() – общая длина эффективных
проводников фазы обмотки, м:
– общая длина эффективных
проводников фазы обмотки, м:
|
|
|
где ![]() – средняя длина витка
обмотки, м;
– средняя длина витка
обмотки, м;
![]() – число витков фазы.
– число витков фазы.
Среднюю длину витка ![]() находят как сумму
прямолинейных пазовых и изогнутых лобовых частей катушки:
находят как сумму
прямолинейных пазовых и изогнутых лобовых частей катушки:
|
|
|
Длина пазовой части ![]() равна конструктивной длине
сердечников машины:
равна конструктивной длине
сердечников машины: ![]() .
.
Длина лобовой части катушки, м:
|
|
|
Окончательно
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Вылет лобовых частей катушки, м:
|
|
|
В этих формулах ![]() – средняя ширина катушки,
м, определяемая по дуге окружности, проходящей по серединам высоты пазов:
– средняя ширина катушки,
м, определяемая по дуге окружности, проходящей по серединам высоты пазов:
|
|
|
где ![]() – укорочение шага обмотки,
для двухслойной обмотки выполненной без укорочения шага, принимаем
– укорочение шага обмотки,
для двухслойной обмотки выполненной без укорочения шага, принимаем ![]() ;
;
![]() и
и ![]() –
коэффициенты, значения которых берем из табл. 8.21 [1, c.334],
–
коэффициенты, значения которых берем из табл. 8.21 [1, c.334], ![]() ,
,
![]() ;
;
![]() – длины вылета прямолинейной части
катушек из паза от торца сердечника до начала отгиба лобовой части, м,
– длины вылета прямолинейной части
катушек из паза от торца сердечника до начала отгиба лобовой части, м, ![]() [1, с.334].
[1, с.334].
Тогда
![]() ;
;
![]() .
.
Относительное значение
![]() .
.
Находим активное сопротивление фазы обмотки ротора:
|
|
|
где ![]() – сопротивление стержня:
– сопротивление стержня:
|
|
|
![]() – сопротивление участка замыкающего
кольца, заключенного между двумя соседними стержнями:
– сопротивление участка замыкающего
кольца, заключенного между двумя соседними стержнями:
|
|
|
где для литой алюминиевой
обмотки ротора ![]() .
.
Окончательно
![]() ;
;
![]() ;
;
![]() .
.
Приводим ![]() к числу витков обмотки
статора:
к числу витков обмотки
статора:
|
|
|
Имеем
![]()
Относительное значение:
![]() .
.
Индуктивное сопротивление фазы обмотки статора:
|
|
|
где ![]() – расчетная длина при
отсутствии радиальных вентиляционных каналов [1, c.337].
– расчетная длина при
отсутствии радиальных вентиляционных каналов [1, c.337].
По табл. 8.24 [1, c.338] (см. рис. 8.50, е) [1]:
|
|
|
где![]() ;
;
![]() ;
;
![]() ;
;
![]() (проводники заполнены пазовой
крышкой);
(проводники заполнены пазовой
крышкой);
![]() ;
;
![]() ;
;
![]() .
.
Тогда
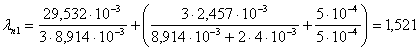
Коэффициент магнитной проводимости лобового рассеяния:
|
|
|
где ![]() и
и ![]() – число пазов на полюс и
фазу и длина лобовой части витка обмотки.
– число пазов на полюс и
фазу и длина лобовой части витка обмотки.
Поэтому
![]() .
.
Коэффициент магнитной проводимости дифференциального рассеяния определяем по формуле:
|
|
|
в которой ![]() находим следующим образом,
учитывая, что при полузакрытых или полуоткрытых пазах статора с учетом скоса
пазов:
находим следующим образом,
учитывая, что при полузакрытых или полуоткрытых пазах статора с учетом скоса
пазов:
|
|
|
Окончательно
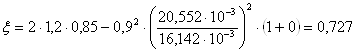 ;
;
![]() ;
;
![]() .
.
Относительное значение
![]() .
.
Индуктивное сопротивление фазы обмотки ротора:
|
|
|
где по табл. 8.25 (см. рис. 8.52, а,ж)
|
|
|
где (см. рис.8.52, а, ж и рис 8.76)
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Тогда
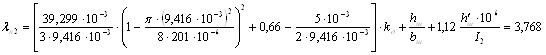
Коэффициент магнитной проводимости лобового рассеяния в роторах с литыми обмотками при замыкающих кольцах, прилегающих к торцам сердечника ротора (см. рис. 8.37,б [1]) используем формулу:
|
|
|
Имеем
![]() .
.
В этих формулах ![]() – средний диаметр
замыкающих колец;
– средний диаметр
замыкающих колец; ![]() – коэффициент
приведения токов в кольце к току в стержне;
– коэффициент
приведения токов в кольце к току в стержне; ![]() и
и
![]() – средние высота и ширина
колец.
– средние высота и ширина
колец.
Коэффициент магнитной проводимости дифференциального рассеяния обмотки короткозамкнутого ротора:
|
|
|
где
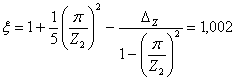
По кривым рис. 8.51, а
[1, с.340] принимаем ![]()
Тогда
![]() .
.
Окончательно
![]() .
.
Приводим ![]() к числу витков обмотки
статора:
к числу витков обмотки
статора:
|
|
|
Тогда
![]()
Относительное значение
![]() .
.
Сравнение параметров проектируемого АД, полученных в данном разделе, с теми же параметрами аналога:
| Величина |
|
|
|
|
| Проектируемый АД |
|
|
|
|
| Аналог | 0,028 | 0,021 | 0,094 | 0,12 |
1.7 Расчет потерь
Потери в асинхронных машинах подразделяют на потери в стали (основные и добавочные), электрические, вентиляционные, механические о добавочные при нагрузке.
Основные потери в стали статоров асинхронных машин по формуле:
|
|
|
где ![]() для стали 2212 –
удельные потери при индукции 1 Тл и частоте перемагничивания 50 Гц;
для стали 2212 –
удельные потери при индукции 1 Тл и частоте перемагничивания 50 Гц;
![]() – показатель степени, учитывающий
зависимость потерь в стали от частоты перемагничивания;
– показатель степени, учитывающий
зависимость потерь в стали от частоты перемагничивания;
![]() и
и ![]() –
коэффициенты, учитывающие влияние на потери в стали неравномерности
распределения потока по сечениям участков магнитопровода и технологических
факторов [1, с.348];
–
коэффициенты, учитывающие влияние на потери в стали неравномерности
распределения потока по сечениям участков магнитопровода и технологических
факторов [1, с.348];
![]() и
и ![]() –
индукция в ярме и средняя индукция в зубцах статора, Тл;
–
индукция в ярме и средняя индукция в зубцах статора, Тл;
![]() и
и ![]() –
масса стали ярма и зубцов статора, кг:
–
масса стали ярма и зубцов статора, кг:
|
|
|
|
|
|
![]() – высота ярма статора, м;
– высота ярма статора, м;
![]() – расчетная высота зубца статора, м;
– расчетная высота зубца статора, м;
![]() – удельная масса стали, в расчетах
принимаем
– удельная масса стали, в расчетах
принимаем ![]() .
.
Тогда
![]() ;
;
![]() ;
;
![]()
Поверхностные потери в роторе:
|
|
|
|
|
|
В этих выражениях ![]() – коэффициент, учитывающий
влияние обработки поверхности головок зубцов ротора на удельные потери.
– коэффициент, учитывающий
влияние обработки поверхности головок зубцов ротора на удельные потери.
Для определения поверхностных потерь вначале находят амплитуду пульсации индукции в воздушном зазоре над коронками зубцов статора и ротора, Тл:
|
|
|
Для зубцов ротора ![]() – это отношение ширины
шлица пазов статора к воздушному зазору:
– это отношение ширины
шлица пазов статора к воздушному зазору:
|
|
|
Для ![]() по рис.8.53 [1, c.349]
по рис.8.53 [1, c.349] ![]()
Окончательно для поверхностных потерь:
![]() ;
;
![]() ;
;
![]()
Пульсационные потери в зубцах ротора:
|
|
|
Для определения пульсационных потерь вначале находиться амплитуда пульсаций индукций в среднем сечении зубцов для зубцов ротора, Тл:
|
|
|
![]() и
и ![]() были
рассчитаны ранее.
были
рассчитаны ранее.
В формуле ![]() :
: ![]() – масса стали зубцов
ротора, кг:
– масса стали зубцов
ротора, кг:
|
|
|
Тогда
![]() ;
;
![]() ;
;
![]() .
.
Сумма добавочных потерь в стали:
|
|
|
Тогда
![]()
Полные потери в стали:
|
|
|
Тогда
![]() .
.
Механические потери на трение в подшипниках и вентиляционные потери в двигателях с радиальной системой вентиляции без радиальных вентиляционных каналов, с короткозамкнутым ротором и вентиляционными лопатками на замыкающих кольцах, Вт:
|
|
|
где ![]() при
при ![]() .
.
![]() .
.
Ток холостого хода двигателя:
|
|
|
где ![]() – реактивная составляющая
тока холостого хода.
– реактивная составляющая
тока холостого хода.
При определении активной составляющей холостого хода принимают, что потери на трение и вентиляцию и потери в стали при холостом ходе двигателя такие же, как и при номинальном режиме.
При этом условии:
|
|
|
Электрические потери в статоре при холостом ходе приближенно принимают равными:
|
|
|
Тогда
![]() ;
;
![]() ;
;
![]() .
.
Коэффициент мощности при холостом ходе:
|
|
|
Окончательно
![]() .
.
1.8 Расчет рабочих характеристик
По (8.184) [1, с.347 ]:
|
|
|
|
|
|
|
|
|
Получим
![]() ;
;
![]() ;
;
![]()
Используем приближенную
формулу, так как ![]() :
:
|
|
|
Тогда
![]() .
.
Активная составляющая тока синхронного холостого хода:
|
|
|
Имеем
![]()
При ![]() можно использовать
приближенный метод, так как в этом случае
можно использовать
приближенный метод, так как в этом случае ![]() и
и
![]() .
.
Тогда
![]() ;
;
![]() ;
;
![]()
![]() .
.
Потери, не изменяющиеся при изменении скольжения:
![]()
Рассчитываем рабочие
характеристики для скольжений ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() , принимая предварительно, что
, принимая предварительно, что ![]() .
.
Номинальные данные спроектированного двигателя:
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Данные расчета сведены в табл.1.
В качестве примера
расчета приведены вычисления для скольжения ![]() :
:
1)
![]() ;
;
2)
![]() ;
;
![]() ;
;
3)
![]() ;
;
4)
![]() ;
;
5)
![]() ;
;
6)
![]() ;
;
7)
![]() ;
;
8)
![]() ;
;
9)
![]() ;
;
10)
![]() ;
;
11)
![]() ;
;
12)
![]() ;
;
13)
![]() ;
;
14)
![]() ;
;
15)
![]() ;
;
16)
![]() ;
;
17)
![]() .
.
Рабочие характеристики представлены на рис. 7.
Таблица 1 - Рабочие характеристики асинхронного двигателя
|
№ п/п |
Расчетные формулы |
Размерность |
Скольжение s |
||||||
| 0,005 | 0,01 | 0,015 | 0,02 | 0,025 | 0,03 | 0,0203 | |||
| 1 |
|
Ом |
40,04 |
20,02 |
13,347 |
10,01 |
8,008 |
6,673 |
9,826 |
| 2 |
|
Ом |
40,3 |
20,28 |
13,606 |
10,27 |
8,268 |
6,933 |
10,122 |
| 3 |
|
Ом |
2,086 |
2,086 |
2,086 |
2,086 |
2,086 |
2,086 |
2,086 |
| 4 |
|
Ом |
40,354 |
20,387 |
13,766 |
10,479 |
8,527 |
7,241 |
10,334 |
| 5 |
|
А |
9,417 |
18,639 |
27,605 |
36,261 |
44,563 |
52,482 |
36,768 |
| 6 |
|
– |
0,999 |
0,995 |
0,988 |
0,979 |
0,969 |
0,957 |
0,979 |
| 7 |
|
– |
0,052 |
0,102 |
0,152 |
0,199 |
0,245 |
0,282 |
0,202 |
| 8 |
|
А |
9,924 |
19,061 |
27,805 |
36,054 |
43,728 |
50,755 |
36,531 |
| 9 |
|
А |
10,903 |
12,324 |
14,600 |
17,635 |
21,320 |
25,540 |
17,839 |
| 10 |
|
А |
15,743 |
22,698 |
31,405 |
40,136 |
48,648 |
56,837 |
40,654 |
| 11 |
|
А |
9,648 |
19,097 |
28,282 |
37,147 |
45,657 |
53,771 |
37,671 |
| 12 |
|
кВт |
11,313 |
21,728 |
31,694 |
41,093 |
49,835 |
57,861 |
41,456 |
| 13 |
|
кВт |
0,165 |
0,392 |
0,750 |
1,226 |
1,801 |
2,459 |
1,258 |
| 14 |
|
кВт |
0,053 |
0,208 |
0,457 |
0,789 |
1,192 |
1,654 |
0,811 |
| 15 |
|
кВт |
0,056 |
0,108 |
0,158 |
0,205 |
0,249 |
0,289 |
0,207 |
| 16 |
|
кВт |
2,8 |
3,234 |
3,892 |
4,746 |
5,768 |
6,927 |
4,803 |
| 17 |
|
кВт |
8,512 |
18,495 |
27,806 |
36,354 |
44,081 |
50,956 |
36,842 |
| 18 |
|
– |
0,752 |
0,821 |
0,877 |
0,886 |
0,885 |
0,878 |
0,885 |
| 19 |
|
– |
0,573 |
0,778 |
0,851 |
0,887 |
0,887 |
0,887 |
0,887 |
После построения рабочих
характеристик уточняем значение номинального скольжения – ![]() .
.
1.9 Расчет пусковых характеристик
Расчет токов с учетом влияния изменения параметров под влиянием эффекта вытеснения тока (без учета влияния насыщения от полей рассеяния).
Учитывая, что индуктивное
сопротивление взаимной индукции ![]() с
уменьшением насыщения магнитопровода увеличивается, в расчете пусковых
характеристик для скольжений
с
уменьшением насыщения магнитопровода увеличивается, в расчете пусковых
характеристик для скольжений ![]() , оно
может быть принято равным:
, оно
может быть принято равным:
|
|
|
Тогда
![]() .
.
Не внося большой
погрешности, в расчетных формулах пусковых режимов пренебрегают сопротивлением ![]() . Это оправдано при токах,
заметно превышающих номинальный, так как электрические потери в обмотках,
возрастающие пропорционально квадрату тока, многократно превышают потери в
стали, для учета которых в схему замещения введен параметр
. Это оправдано при токах,
заметно превышающих номинальный, так как электрические потери в обмотках,
возрастающие пропорционально квадрату тока, многократно превышают потери в
стали, для учета которых в схему замещения введен параметр ![]() .
.
При этом допущениях коэффициент
|
|
|
Имеем
![]() .
.
Максимальный момент двигателя вначале определяем по приближенному значению критического скольжения:
|
|
|
Получим
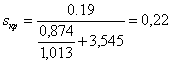 .
.
По рис. 2. определяем:
![]() .
.
Данные расчета остальных точек сведены в табл.2.
В качестве примера
приведен расчет для ![]() :
:
1. ![]() ;
;
2. ![]() : по кривой рис. 8.57 [1, c.366]
: по кривой рис. 8.57 [1, c.366] ![]() ;
;
3. ![]() ;
;
4. ![]() ,
,
где ![]()
где ![]()
5. ![]() ;
;
6. ![]() ;
;
7. ![]() ; по кривой рис. 8.58 [1, c.366]
; по кривой рис. 8.58 [1, c.366] ![]() ;
;
8. ![]() ,
,
где
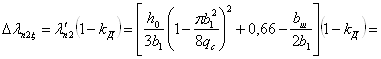
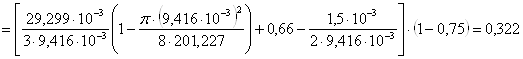
9. 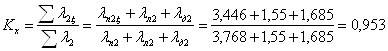 ;
;
10.
![]() ;
;
11.
![]() ;
;
12.
![]()
13.
![]() ;
;
14.
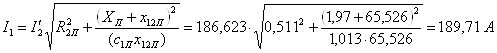 .
.
Таблица 2 - Пусковые характеристики асинхронного двигателя
|
№ п/п |
Расчетные формулы |
Размерность |
Скольжение s |
|||||
| 1 | 0,8 | 0,5 | 0,2 | 0,1 |
0,22=sкр |
|||
| 1 |
|
– |
1,932 |
1,727 |
1,366 |
0,864 |
0,611 |
– |
| 2 |
|
– |
0,97 |
0,62 |
0,34 |
0,089 |
0,61 |
– |
| 3 |
|
мм |
15,416 |
18,747 |
22,664 | 28,935 | 29,998 | 28,637 |
| 4 |
|
– |
1,638 |
1,389 |
1,199 |
1 |
1 |
1 |
| 5 |
|
– |
1,332 |
1,202 |
1,104 |
1 |
1 |
1 |
| 6 |
|
Ом |
0,254 |
0,229 |
0,211 |
0,19 |
0,19 |
0,19 |
| 7 |
|
– |
0,75 |
0,82 |
0,91 |
0,97 |
0,98 |
0,97 |
| 8 |
|
– |
3,446 |
3,536 |
3,652 |
3,729 |
3,742 |
3,729 |
| 9 |
|
– |
0,953 |
0,966 |
0,983 |
0,994 |
0,966 |
0,994 |
| 10 |
|
Ом |
1,082 |
1,096 |
1,115 |
1,128 |
1,13 |
1,128 |
| 11 |
|
Ом |
0,511 |
0,544 |
0,680 |
1,220 |
2,186 |
1,128 |
| 12 |
|
Ом |
1,97 |
1,985 |
2,005 |
2,017 |
2,019 |
2,017 |
| 13 |
|
А |
186,623 |
184,557 |
179,487 |
161,172 |
127,67 |
164,383 |
| 14 |
|
А |
195,71 |
187,652 |
182,552 |
163,974 |
129,94 |
167,236 |
Расчет токов с учетом влияния изменения параметров под влиянием эффекта вытеснения тока и насыщения от полей рассеяния.
Расчет производим для
точек характеристик, соответствующих ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() при этом используем
значения токов и сопротивлений для тех же скольжений с учетом влияния
вытеснения тока (табл. 2).
при этом используем
значения токов и сопротивлений для тех же скольжений с учетом влияния
вытеснения тока (табл. 2).
Данные расчета сведены в табл. 3.
В качестве примера
приведен расчет для ![]() .
.
1.
Ориентировочно
для расчета пускового режима принимаем ![]() по
рекомендациям [1, с.370]
по
рекомендациям [1, с.370]
2. Определяем среднюю магнитодвижущую силу, отнесенную к одному пазу обмотки статора:
3.
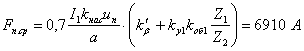 ;
;
4.
![]() ;
;
5.
![]() ;
;
6.
![]() ;
;
7.
![]() ;
;
8.
![]() ;
;
9.
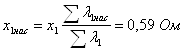 ;
;
10.
![]() ;
;
11.
![]() ;
;
12.
![]() ;
;
13.
![]() ;
;
14.
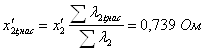 ;
;
15.
![]() ;
;
16.
![]() ;
;
17.
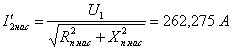 ;
;
18.
 ;
;
19.
![]() ;
;
20.
![]() ;
;
21.
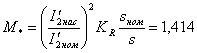 .
.
Полученный в расчете
коэффициент насыщения ![]() отличается
от принятого
отличается
от принятого ![]() приблизительно до 3%, что
вполне допустимо.
приблизительно до 3%, что
вполне допустимо.
Таблица 3 - Пусковые характеристики асинхронного двигателя с короткозамкнутым ротором с учетом вытеснения тока и насыщения от полей рассеяния
|
№ п/п |
Расчетные формулы |
Размерность |
Скольжение s |
|||||
| 1 | 0,8 | 0,5 | 0,2 | 0,1 |
0,22=sкр |
|||
| 1 |
|
– |
1,35 |
1,3 |
1,25 |
1,1 |
1,05 |
1,07 |
| 2 |
|
А |
6910 |
6581 |
6111 |
4778 |
3618 |
3905 |
| 3 |
|
Тл |
4,697 |
4,471 |
4,151 | 3,246 | 2,458 | 2,650 |
| 4 |
|
– |
0,48 |
0,52 |
0,55 |
0,69 |
0,75 |
0,72 |
| 5 |
|
мм |
6,76 |
6,24 |
5,85 |
4,03 |
3,25 |
3,64 |
| 6 |
|
– |
1,14 |
1,182 |
1,199 |
1,26 |
1,297 |
1,278 |
| 7 |
|
– |
0,773 |
0,837 |
0,866 |
1,111 |
1,208 |
1,159 |
| 8 |
|
Ом |
0,59 |
0,597 |
0,693 |
0,629 |
0,641 |
0,635 |
| 9 |
|
– |
1,007 |
1,007 |
1,008 |
1,008 |
1,008 |
1,008 |
| 10 |
|
мм |
10,4 |
9,6 |
9 |
6,2 |
5 |
5,6 |
| 11 |
|
– |
1,878 |
1,957 |
2,172 |
2,355 |
2,437 |
2,387 |
| 12 |
|
– |
1,291 |
1,399 |
1,470 |
1,856 |
2,618 |
1,957 |
| 13 |
|
Ом |
0,739 |
0,769 |
0,817 |
0,906 |
0,945 |
0,925 |
| 14 |
|
Ом |
0,564 |
0,6 |
0,714 |
1,229 |
2,122 |
1,906 |
| 15 |
|
Ом |
1,335 |
1,372 |
1,425 |
1,542 |
1,594 |
1,567 |
| 16 |
|
А |
262,275 |
253,766 |
238,34 |
192,647 |
143,19 |
157,84 |
| 17 |
|
А |
264,701 |
256,213 |
240,783 |
194,851 |
144,931 |
159,761 |
| 18 |
|
– |
1,317 |
1,289 |
1,254 |
1,142 |
1,071 |
1,08 |
| 19 |
|
– |
6,606 |
6,394 |
6,009 |
4,883 |
3,751 |
3,984 |
| 20 |
|
– |
1,414 |
1,475 |
1,783 |
2,58 |
2,778 |
2,979 |
Определяем критическое скольжение:
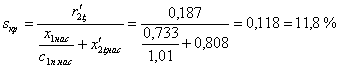 , после чего рассчитываем точку характеристики,
соответствующую
, после чего рассчитываем точку характеристики,
соответствующую ![]() :
: ![]() .
.
Кратности пускового и максимального моментов и пускового тока спроектированного двигателя удовлетворяют требованиям ГОСТ.
1.10 Тепловой и вентиляционный расчет
Превышение температуры внутренней поверхности сердечника статора над температурой воздуха внутри двигателя, °С:
|
|
|
По табл. 8.33 [1, c.402] принимаем ![]() .
.
Электрические потери в
обмотке статора делятся на потери в пазовой части ![]() и
потери в лобовых частях катушек
и
потери в лобовых частях катушек ![]() :
:
|
|
|
|
|
|
где ![]() – коэффициент увеличения
потерь, для обмоток с изоляцией класса нагревостойкости F
– коэффициент увеличения
потерь, для обмоток с изоляцией класса нагревостойкости F ![]()
Тогда
![]() .
.
По рис. 8.70,б [1,
с.400] принимаем среднее значение коэффициента теплоотдачи с поверхности ![]() .
.
Имеем
![]() .
.
Перепад температуры в изоляции пазовой части обмотки статора, °С:
|
|
|
где ![]() – расчетный периметр
поперечного сечения паза статора, равный для полузакрытых трапецеидальных
пазов:
– расчетный периметр
поперечного сечения паза статора, равный для полузакрытых трапецеидальных
пазов:
|
|
|
где ![]() ,
, ![]() и
и ![]() – размеры паза в штампе
(рассчитаны ранее).
– размеры паза в штампе
(рассчитаны ранее).
Для изоляции класса
нагревостойкости F ![]() , по рис. 8.72 [1, с.402] для
, по рис. 8.72 [1, с.402] для ![]() находим
находим ![]() .
.
Тогда
![]() ;
;
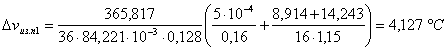 .
.
Перепад температуры по толщине изоляции лобовых частей:
|
|
|
Тогда
![]() ;
;
![]() ;
;
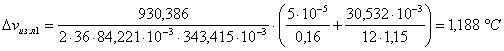 .
.
Превышение температуры наружной поверхности лобовых частей над температурой воздуха внутри двигателя:
|
|
|
Имеем
![]() .
.
Среднее превышение температуры обмотки статора над температурой воздуха внутри двигателя:
|
|
|
Получим
![]() .
.
Превышение температуры воздуха внутри двигателя над температурой окружающей среды:
|
|
|
где ![]() для
для ![]() ;
;
![]() – сумма потерь, отводимых в воздух
внутри двигателя, Вт:
– сумма потерь, отводимых в воздух
внутри двигателя, Вт:
|
|
|
Где
|
|
|
где ![]() – сумма всех потерь в
двигателе при номинальном режиме и расчетной температуре,
– сумма всех потерь в
двигателе при номинальном режиме и расчетной температуре, ![]() из табл. 1 для
из табл. 1 для ![]() .
.
Эквивалентная поверхность охлаждения корпуса с учетом поверхности ребер станины:
|
|
|
где ![]() – условный периметр
поперечного сечения ребер корпуса двигателя; значение которого принимаем по рис.
8.73 [1, с.404]
– условный периметр
поперечного сечения ребер корпуса двигателя; значение которого принимаем по рис.
8.73 [1, с.404] ![]() для
для ![]() .
.
Окончательно
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Среднее превышение температуры обмотки статора над температурой окружающей среды:
|
|
|
Тогда
![]() .
.
Проверка условий охлаждения двигателя.
Требуемый для двигателей со степенью защиты IP44 охлаждения расход воздуха:
|
|
|
где ![]() – коэффициент, учитывающий
изменение условий охлаждения по длине поверхности корпуса, обдуваемого наружным
вентилятором:
– коэффициент, учитывающий
изменение условий охлаждения по длине поверхности корпуса, обдуваемого наружным
вентилятором:
|
|
|
Коэффициент ![]() принимаем по рекомендациям
[1, с.407]
принимаем по рекомендациям
[1, с.407] ![]() .
.
Тогда
![]() ;
;
![]() ;
;
Расход воздуха, обеспечиваемый наружным вентилятором, может быть определен по формуле:
|
|
|
Тогда
![]() .
.
Нагрев частей двигателя находится в допустимых пределах (по табл.7.1 [1, с.212].
Вентилятор
обеспечивает необходимый расход воздуха, так как ![]() (по требованиям [1, с.407]).
(по требованиям [1, с.407]).
Вывод: спроектированный двигатель отвечает поставленным в техническом задании требованиям.
1.11 Механический расчет
Электрические машины общего назначения в большинстве случаев выполняют с горизонтальным расположением вала. В этом случае вал несет на себе всю массу вращающихся частей, через него передается вращающий момент машины. При сочленении машины с исполнительным механизмом (для двигателя) или с приводным двигателем (для генератора) через ременную или зубчатую передачу, а также и через муфту на вал действуют дополнительные изгибающие силы. Кроме того, на вал могут действовать силы одностороннего магнитного притяжения, вызванные магнитной несимметрией, усилия, появляющиеся из-за наличия небаланса вращающихся частей, а также усилия, возникающие при появлении крутильных колебаний. Правильно сконструированный вал должен быть достаточно прочным, чтобы выдержать все действующие на него нагрузки без появления остаточных деформаций. Вал должен также иметь достаточную жесткость, чтобы при работе машины ротор не задевал о статор. Критическая частота вращения вала должна быть значительно больше рабочих частот вращения машины. При критической частоте вращения вынуждающая сила небаланса имеет частоту, равную частоте собственных поперечных колебаний вала (т.е. наступает явление резонанса), при которой резко увеличиваются прогиб вала и вибрация машины.
Валы изготовляют из углеродистых сталей, преимущественно из стали марки 45. Для повышения механических свойств сталей их подвергают термической обработке.
Размеры вала определяют при разработке конструкции. Валы имеют ступенчатую форму с большим диаметром в месте посадки магнитопровода ротора. Число ступеней вала зависит от количества узлов машины, размещаемых на нем (магнитопровод, коллектор, подшипники, вентилятор, контактные кольца и т.д.). При переходе с одного диаметра вала на другой для предупреждения недопустимой концентрации напряжений в местах переходов должны быть предусмотрены закругления (галтели) максимально возможного радиуса. Отношение радиуса галтели к диаметру вала должно быть больше 0,05. По этой же причине не следует применять отношение диаметров соседних ступеней вала более 1,3. Иногда для фиксации положения пакета магнитопровода ротора на валу предусматривается упорный буртик. Диаметр вала, см, в той его части, где размещается магнитопровод, предварительно можно выбрать по формуле:
|
|
|
где ![]() – номинальная мощность, кВт;
– номинальная мощность, кВт;
![]() – номинальная частота вращения
ротора, об/мин;
– номинальная частота вращения
ротора, об/мин;
![]() – коэффициент, значение которого
принимаем по рекомендациям [2, c.231]
равным
– коэффициент, значение которого
принимаем по рекомендациям [2, c.231]
равным ![]() .
.
Тогда
 .
.
По рекомендациям [3, с.78] принимаем основные размеры: a=53,5 мм; d3=80 мм; d2=65 мм; L1=458 мм; L2=229 мм; а1=53,5 мм.
Размеры свободного конца
вала выбираем в соответствии с ГОСТ 18709-73 и ГОСТ 20839-75 по табл. 11.1
([1, с.233]): ![]() ,
, ![]() .<
.<
Принимая, что ротор асинхронного двигателя представляет собой сплошной цилиндр с плотностью 8300 кг/м3, его массу можно определить по формуле:
|
|
|
Имеем
![]() .
.
Прогиб определяем по формуле:
|
|
|
Тогда
![]() .
.
Электрическая машина
сочленяется с исполнительным механизмом одним из указанных способов: через
ременную передачу, зубчатую передачу или через упругую муфту. При работе машины
возникают поперечные силы ![]() ,
приложенные к выступающему концу вала и соответственно вызванные натяжением
ремня, давлением на зубец шестерни или же неточностью сопряжения валов и изготовлением
деталей муфты.
,
приложенные к выступающему концу вала и соответственно вызванные натяжением
ремня, давлением на зубец шестерни или же неточностью сопряжения валов и изготовлением
деталей муфты.
Эту силу ![]() можно определить по
формуле:
можно определить по
формуле:
|
|
|
где ![]() – номинальный вращающий
момент,
– номинальный вращающий
момент, ![]() :
:
|
|
|
![]() – коэффициент, принимаем равным
– коэффициент, принимаем равным ![]() , при условии передачи
упругой муфтой;
, при условии передачи
упругой муфтой;
![]() – радиус делительной окружности
шестерни или радиус по центрам пальцев муфты или окружности шкива, м.
– радиус делительной окружности
шестерни или радиус по центрам пальцев муфты или окружности шкива, м.
Получим:
![]() ;
; ![]() .
.
Вал разбиваем на три участка: a, b и с.
По табл. 11.3; 11.4 [2, с. 236]:
![]() ;
;
![]() ;
;
![]() .
.
Прогиб вала, м,
под действием силы ![]() на участке,
соответствующем середине магнитопровода, равна:
на участке,
соответствующем середине магнитопровода, равна:
|
|
|
где ![]() – модуль упругости;
– модуль упругости;
Тогда
![]() .
.
Сила ![]() вызывает дополнительный
прогиб вала под серединой магнитопровода:
вызывает дополнительный
прогиб вала под серединой магнитопровода:
|
|
|
![]() .
.
Первоначальное смещение ротора:
|
|
|
![]() .
.
Силу одностороннего магнитного притяжения определяем по формуле:
|
|
|
![]() .
.
Сила ![]() вызывает дополнительный
прогиб вала, который пропорционален прогибу
вызывает дополнительный
прогиб вала, который пропорционален прогибу ![]() от
силы тяжести:
от
силы тяжести:
|
|
|
![]() .
.
Установившийся прогиб под действием силы магнитного притяжения:
|
|
|
![]() .
.
Результирующий прогиб вала определяется для наихудшего случая:
|
|
|
![]() ,
,
эта величина составляет 0,266 % от d, что является допустимым.
Критическую частоту вращения находим по приближённой формуле:
|
|
|
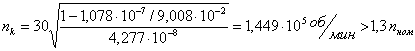 .
.
В расчёте на прочность
принимаем коэффициент перегрузки ![]() [2, с.
239].
[2, с.
239].
Напряжение на свободном конце вала в сечении А:
|
|
|
где ![]() – изгибающий момент;
– изгибающий момент;
|
|
|
![]() – момент
сопротивления при изгибе;
– момент
сопротивления при изгибе;
|
|
|
Окончательно:
![]() ;
;
![]() ;
;
![]() .
.
Напряжение на свободном конце вала в сечении B:
|
|
|
где ![]() – изгибающий момент;
– изгибающий момент;
|
|
|
![]() – момент
сопротивления при изгибе;
– момент
сопротивления при изгибе;
|
|
|
Окончательно:
![]() ;
;
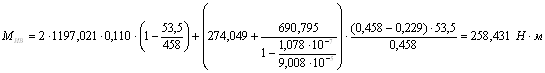 ;
;
![]() .
.
Напряжение на свободном конце вала в сечении C:
|
|
|
|
|
|
![]() – момент
сопротивления при изгибе;
– момент
сопротивления при изгибе;
|
|
|
Окончательно:
![]() ;
;
 ;
;
![]() .
.
Напряжение на свободном конце вала в сечении D:
|
|
|
где ![]() – изгибающий момент;
– изгибающий момент;
|
|
|
![]() – момент
сопротивления при изгибе;
– момент
сопротивления при изгибе;
|
|
|
![]() ;
;
 ;
;
![]() .
.
Напряжения во всех
сечениях не превышают предела текучести ![]() для
стали марки 45.
для
стали марки 45.
Выбор подшипников.
Для определения
радиальной нагрузки на подшипники ![]() и
и ![]() будем исходить из
наихудшего случая.
будем исходить из
наихудшего случая.
|
|
|
|
|
|
![]()
![]() .
.
Приведённая динамическая нагрузка равна:
|
|
|
где ![]() – коэффициент учитывающий
характер нагрузки двигателя.
– коэффициент учитывающий
характер нагрузки двигателя.
![]() ;
;
![]() .
.
Динамическая грузоподъёмность:
|
|
|
где ![]() – требуемый срок службы.
– требуемый срок службы.
![]() ;
;
![]() .
.
Выбираем шарикоподшипники радиальные однорядные по ГОСТ 8339-75.
ОПОРА A:
| Тип |
|
|
|
|
|
| 213 | 65 | 120 | 23 | 44000 | 5000 |
ОПОРА В:
| Тип |
|
|
|
|
|
| 313 | 65 | 140 | 35 | 71300 | 4000 |
2. Моделирование двигателя
Моделирование прямого пуска спроектированного двигателя выполняется на холостом ходу с последующей нагрузкой после выхода на установившийся режим (через 5с) номинальным моментом (Mном=119,702 Н·м).
Моделирование выполняется в среде ПМК МИК-АЛ с учетом вышеуказанных замечаний без учета эффекта вытеснения тока с постоянными параметрами схемы замещения машины в двух вариантах:
– для параметров номинального режима;
– для параметров пускового режима.
Текст программы в ПМК МИК-АЛ для номинального режима:
$ВВОД
$УРАВН(Т)
{* Параметры НОМИНАЛЬНОГО режима *}
u:=537.4; P:=1; Rs:=0.253; Rrw:=0.191; Wk:=0;
Lm:=0.1223; Ls:=0.12507; Lr:=0.12588; J:=1.5; Mc:=0;
{* Питающие напряжения *}
Usa=N#sin_t(u:ПАР=1,314.15926,0.0);
Usb=N#sin_t(u:ПАР=1,314.15926,4.1888);
Usc=N#sin_t(u:ПАР=1,314.15926,2.0944);
Usal1=(-0.4082483)*(Usb+Usc)+0.8164967*Usa;
Usbet1=0.7071068*(Usb-Usc);
{*Преоразование в произвольную систему координат*}
FI'=P*Wk;
Usu=Usal1*N#cos(FI)+Usbet1*N#sin(FI);
Usv=-Usal1*N#sin(FI)+Usbet1*N#cos(FI);
{* Потокосцепления статора и ротора *}
Fsu'=Usu-Isu*Rs+P*Wk*Fsv;
Fsv'=Usv-Isv*Rs-P*Wk*Fsu;
Fru'=0-Iru*Rrw+Frv*P*(Wk-W);
Frv'=0-Irv*Rrw-Fru*P*(Wk-W);
{* Токи статора и ротора *}
{* СЛАУ *}
СЛАУ: Isu,Iru;
Ls*Isu+Lm*Iru=Fsu;
Lr*Iru+Lm*Isu=Fru;
СЛАУ: Isv,Irv;
Ls*Isv+Lm*Irv=Fsv;
Lr*Irv+Lm*Isv=Frv;
{* Электромагнитный момент и скорость *}
M=P*(Fsu*Isv-Fsv*Isu);
W'=(M-Mc)/J;
IstA=Isu/1.73;
КОНЕЦ
* Задание на эксперимент *
ИНТ RKT4
ШАГ ИНТ=0.001
ШАГ ВЫВ=0.006
КОН ВР=5
ВЫВОД Isu,Isv,IstA,Iru,Irv,Fsu,Fsv,W,M
ДИСПЛ W,M,Isu,Iru
$КОН
$СТОП
Текст программы в ПМК МИК-АЛ для пускового режима:
$ВВОД
$УРАВН(Т)
{* Параметры ПУСКОВОГО режима *}
u:=537.4; P:=1; Rs:=0.253; Rrw:=0.254; Wk:=0;
Lm:=0.208; Ls:=0.212; Lr:=0.21258; J:=1.5; Mc:=0;
{* Питающие напряжения *}
Usa=N#sin_t(u:ПАР=1,314.15926,0.0);
Usb=N#sin_t(u:ПАР=1,314.15926,4.1888);
Usc=N#sin_t(u:ПАР=1,314.15926,2.0944);
Usal1=(-0.4082483)*(Usb+Usc)+0.8164967*Usa;
Usbet1=0.7071068*(Usb-Usc);
{*Преоразование в произвольную систему координат*}
FI'=P*Wk;
Usu=Usal1*N#cos(FI)+Usbet1*N#sin(FI);
Usv=-Usal1*N#sin(FI)+Usbet1*N#cos(FI);
{* Потокосцепления статора и ротора *}
Fsu'=Usu-Isu*Rs+P*Wk*Fsv;
Fsv'=Usv-Isv*Rs-P*Wk*Fsu;
Fru'=0-Iru*Rrw+Frv*P*(Wk-W);
Frv'=0-Irv*Rrw-Fru*P*(Wk-W);
{* Токи статора и ротора *}
{* СЛАУ *}
СЛАУ: Isu,Iru;
Ls*Isu+Lm*Iru=Fsu;
Lr*Iru+Lm*Isu=Fru;
СЛАУ: Isv,Irv;
Ls*Isv+Lm*Irv=Fsv;
Lr*Irv+Lm*Isv=Frv;
{* Электромагнитный момент и скорость *}
M=P*(Fsu*Isv-Fsv*Isu);
W'=(M-Mc)/J;
IstA=Isu/1.73;
КОНЕЦ
*Задание на эксперимент*
ИНТ RKT4
ШАГ ИНТ=0.001
ШАГ ВЫВ=0.006
КОН ВР=5
ВЫВОД Isu,Isv,IstA,Iru,Irv,Fsu,Fsv,W,M
ДИСПЛ W,M,Isu,Iru
$КОН
$СТОП
Результаты моделирования пускового и номинального режимов в среде ПМК МИК-АЛ представлены на рис. 3, 4, 5, 6.
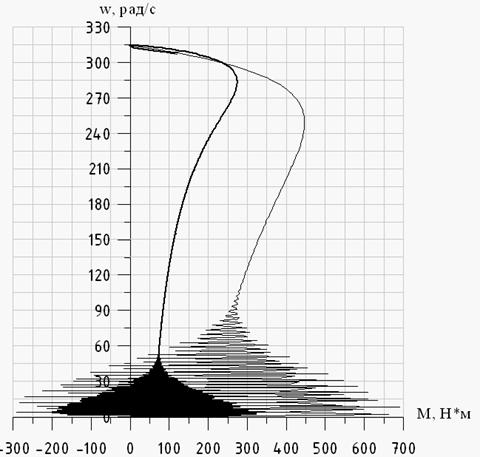
Рис. 3 - Динамическая механическая
характеристика ![]() : ––––– для номинального режима; – – – для
пускового режима.
: ––––– для номинального режима; – – – для
пускового режима.
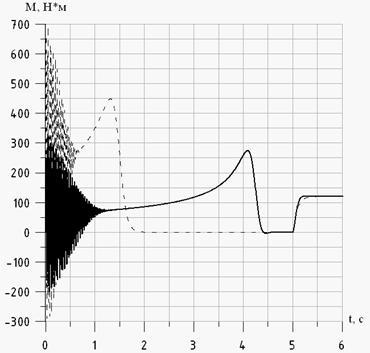
Рис. 4 - Зависимость электромагнитного момента от времени: ––––– для номинального режима; – – – для пускового режима
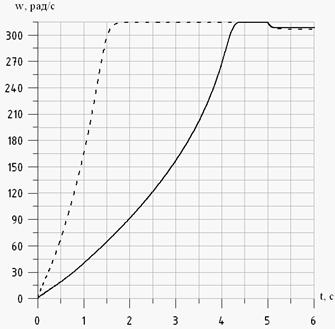
Рис. 5 - Зависимость угловой частоты вращения ротора от времени: ––––– для номинального режима; – – – для пускового режима
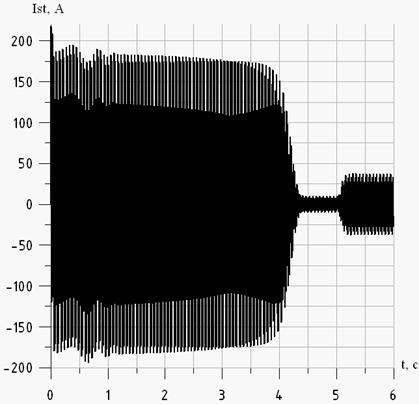
Рис. 6 - Зависимость тока фазы А статора от времени для номинального режима
3. Исследовательская часть
Целью исследовательской
части является исследование влияния закона управления ![]() на динамические пусковые
характеристики.
на динамические пусковые
характеристики.
Частотный способ регулирования частоты вращения позволяет применять более надежные и дешевые асинхронные двигатели с короткозамкнутым ротором. Однако для изменения частоты питающего напряжения требуется наличие источника электрического тока переменной частоты. В качестве последнего используют либо синхронные генераторы с переменной частотой вращения и чаще всего приоритетнее использование преобразователей на полупроводниковых элементах (тиристорах и IGBT транзисторах) [4].
В данном разделе будет
произведено моделирование в среде Matlab v6.1 пуска
электропривода с асинхронным двигателем с короткозамкнутым ротором по закону ![]() при питании каждой фазы от
однофазного инвертора, спроектированным в данной курсовой работе.
при питании каждой фазы от
однофазного инвертора, спроектированным в данной курсовой работе.
Моделирование производится
с постоянным абсолютным скольжением для двух случаев: при ![]() и скольжении, близком к
критическому
и скольжении, близком к
критическому ![]() ; пуск
выполняется с увеличением частоты от 0 до 50 Гц. Наброс нагрузки со значением номинального
момента производится при t=6 c.
; пуск
выполняется с увеличением частоты от 0 до 50 Гц. Наброс нагрузки со значением номинального
момента производится при t=6 c.
Структурная схема в среде Matlab v6.1 представлена на рис. 7.
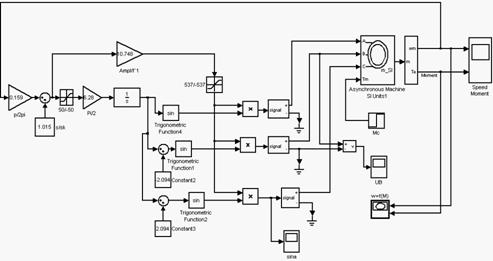
Рис. 7 - Структурная
схема пуска АД по закону ![]()
Результаты моделирования представлены на рис. 8, 9, 10, 11.
Результаты моделирования в среде Matlab v6.1:
![]()
![]()
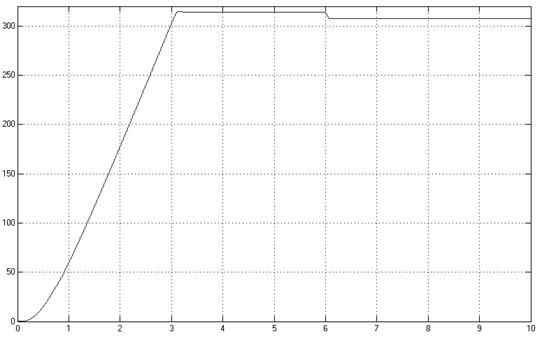
Рис. 8 - Зависимость
угловой скорости от времени при ![]()
![]()
![]()
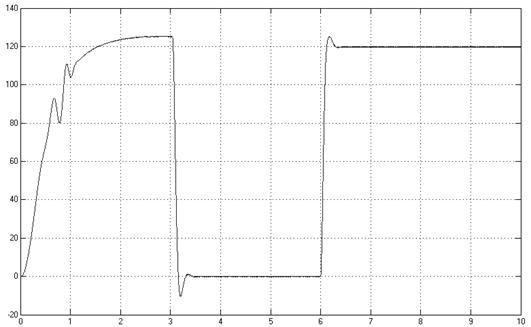
Рис. 9 - Зависимость
момента от времени при ![]()
![]()
![]()
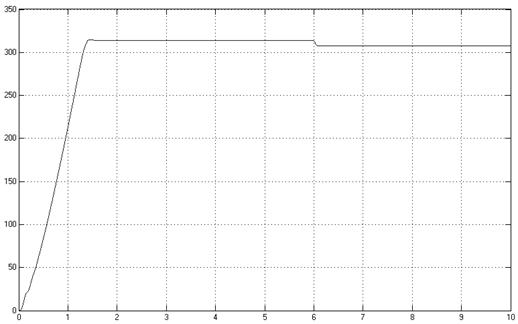
Рис. 10 - Зависимость
угловой скорости от времени при ![]()
![]()
![]()
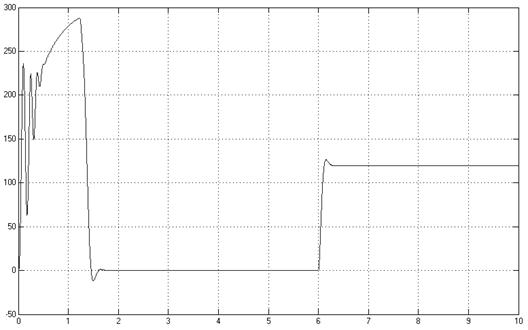
Рис. 11 - Зависимость
момента от времени при ![]()
4. Выбор схемы управления двигателем
Выбор схемы управления производим по рекомендациям [5] с учетом требований задания курсового проекта:
– напряжение сети 660 В
– мощность сети ограниченная
– тип электропривода реверсивный, регулируемый
– характер нагрузки вентиляторная
– условия пуска при постоянном моменте
– требования к регулированию скорости (для регулируемых электроприводов) (0,1 – 1,5)ωном
Схема управления АИН АД представлена на рис. 12.
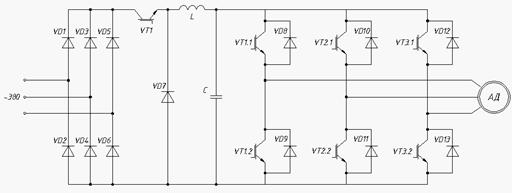
Рис. 12 - Автономный инвертор напряжения на IGBT транзисторах
Трехфазное напряжение, подаваемое из сети, поступает на выпрямитель сформированный из диодов VD1 … VD6, в котором происходит выпрямление этого напряжения. За счет IGBT транзистора VT1 и диода VD7 имеется возможность ограничивать напряжение, подаваемое на автономный инвертор напряжения, собранный на IGBT транзисторах VT1.1 … VT3.2 и диодах VD8 … VD13.
Для уменьшения пульсаций преобразования тока, в схеме установлен дроссель L с достаточно большой индуктивностью, а с помощью конденсатора С происходит уменьшение пульсаций напряжения.
Заключение
В заключение хотелось бы отметить, что поставленная цель курсового проектирования, т.е. освоение основных приемов проектирования трехфазного асинхронного двигателя с короткозамкнутым ротором в принципе была достигнута, хотя и потребовала значительного времени для нахождения оптимальных параметров расчета, поэтому основная вычислительная часть курсового проекта была произведена на ЭВМ.
При выполнении курсового проекта был решен ряд задач, спроектированный двигатель по условиям задания удовлетворяет условиям пуска; в результате теплового расчёта было установлено, что вентилятор двигателя обеспечивает достаточное его охлаждение и защиту от перегрева.
В ходе расчета каждого раздела курсового проекта осуществлялось сравнения с аналогом проектируемого двигателя.
Анализируя расхождения данных, приведенных в аналоговом двигателе и полученных в результате расчетов, необходимо отметить, что эти расхождения, хотя и минимальны, имеют место в результате приближенного определения электромагнитных нагрузок, выбора значений по кривым намагничивания и т.п., поэтому это наложило свой отпечаток на рассчитанные данные.
Элементы механической части были выбраны в соответствии с условиями прочности и износостойкости в продолжительном режиме работы.
В результате моделирования спроектированного двигателя были определены характеристики двигателя с параметрами номинального и пускового режима.
Исследовательской частью данного курсового проекта являлось исследование влияния закона управления U/f=const на динамические пусковые характеристики.
В ходе исследования было установлено, что этот способ позволяет поддерживать максимальный момент, учитывая постоянство магнитного потока.
Спроектированный двигатель в целом удовлетворяет техническому заданию и требованиям, предъявляемым при разработке новых двигателей.
Список литературы
1. Копылов И.П. Проектирование электрических машин: том 1./Под ред. И.П. Копылова. – М.: Энергоатомиздат, 1993.
2. Копылов И.П. Проектирование электрических машин: том 2./Под ред. И.П. Копылова. – М.: Энергоатомиздат, 1993.
3. Асинхронные двигатели серии 4А: Справ./ А.Э. Кравчик и др.- М.: Энергоиздат, 1982. – 504 с.
4. Радин В.И., Брускин Д.Э., Зорохович А.Е., Электрические машины: асинхронные машины. Под ред. И.П. Копылова. – М.: Энергоатомиздат, 1988.
5. Бурков А.Т. Электронная техника и преобразователи. - М. Транспорт, 1999.- 464 с.
6. Герман-Галкин С.Г. Компьютерное моделирование полупроводниковых систем. Matlab 6.0.- Санкт-Петербург: Корона принт, 2001.-320 с.
7. Ключев В.И. Теория электропривода. – М: Энергоатомиздат, 2001. –704 с.
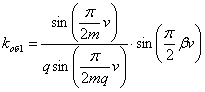 ,
, ,
, ,
, .
. ,
, ,
, .
. .
. .
. ,
, ,
, ,
,
 .
.
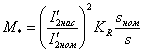
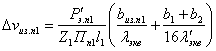 ,
,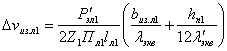 .
.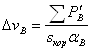 ,
,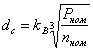 ,
, .
. ;
; ;
; ;
;