Курсовая работа: Специфика проведения измерений и обработки результатов
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
ПО ДИСЦИПЛИНЕ
Метрология, стандартизация и технические измерения
Специфика проведения измерений и обработки результатов
Условие задания
При однократном измерении физической величины получено показание средства измерения X = 10. Определить, чему равно значение измеряемой величины, если экспериментатор обладает априорной информацией о средстве измерений и условиях выполнения измерений согласно данным таблицы 1.
Экспериментальные данные:
![]()
Информация о средстве измерения:
Вид закона распределения нормальный
Значение
оценки среднего квадратичного отклонения ![]()
Доверительная
вероятность ![]()
Мультипликативная
поправка ![]()
Расчет
Предел, в котором находится значение измеряемой величины без учета поправки определяется как:
![]() ;
; ![]() ,
,
где Е - доверительный интервал. Значение Е определяется в зависимости от закона распределения вероятности результата измерения. Для нормального закона
![]() ,
,
где t - квантиль распределения для заданной доверительной
вероятности. Его выбирают из таблицы интегральной функции нормированного
нормального распределения ![]() , при этом следует учитывать, что
, при этом следует учитывать, что ![]() . t = 1,64 при P=0,9
. t = 1,64 при P=0,9
![]() .
.
Используя правила округления, получим:
![]() .
.
С учетом поправки значение измеряемой величины определяется как:
![]() ;
; ![]() .
.
Вносим мультипликативную поправку:
![]() ,
, ![]() ,
,![]() .
.
Записываем результат:
![]() <Q<
<Q<![]() ; P=0,9
; P=0,9
Задание 2. Многократное измерение
Условие задания
При
многократном измерении одной и той же физической величины получена серия из 24
результатов измерений ![]() . Эти результаты после внесения
поправок представлены в таблице. Определить результат измерения.
. Эти результаты после внесения
поправок представлены в таблице. Определить результат измерения.
|
|
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|
|
485 | 484 | 486 | 482 | 483 | 484 | 484 | 481 |
|
|
9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|
|
485 | 485 | 485 | 492 | 484 | 481 | 480 | 481 |
|
|
17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
|
|
484 | 485 | 485 | 484 | 483 | 483 | 485 | 492 |
Для
обработки результатов измерений необходимо исключить ошибки. Число измерений
лежит в диапазоне 10…15<n<40…50.
Поэтому исключение ошибок проводится на основе ![]() критерия.
критерия.
Определяем среднее арифметическое и среднеквадратическое отклонение результатов измерений.
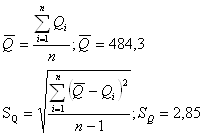
Далее
определяем значения ![]() критерия для каждого значения
результата измерений
критерия для каждого значения
результата измерений ![]() по формуле:
по формуле:
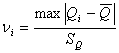
В
соответствии с доверительной вероятностью ![]() с учетом
с учетом ![]() находим из соответствующей
таблицы значение
находим из соответствующей
таблицы значение ![]() , которое зависит от числа
измерений
, которое зависит от числа
измерений ![]() и
и
![]() .
.
![]()
При ![]()
![]() , следовательно значение
492 исключаем как ошибку.
, следовательно значение
492 исключаем как ошибку.
Исключение
ошибок продолжается до тех пор, пока не будет выполнятся условие ![]() .
.
![]()
|
|
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|
|
485 | 484 | 486 | 482 | 483 | 484 | 484 | 481 |
|
|
9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
|
|
485 | 485 | 485 | 484 | 481 | 480 | 481 | 484 |
|
|
17 | 18 | 19 | 20 | 21 | 22 | ||
|
|
485 | 485 | 484 | 483 | 483 | 485 |
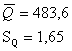
Заново
определяем значения ![]() критерия для каждого значения
результата измерений
критерия для каждого значения
результата измерений ![]() по формуле:
по формуле:
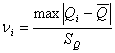
В
соответствии с доверительной вероятностью ![]() с учетом
с учетом ![]() находим из соответствующей
таблицы значение
находим из соответствующей
таблицы значение ![]() , которое зависит от числа
измерений
, которое зависит от числа
измерений ![]() и
и
![]() .
.
![]()
Условие ![]() выполняется для
всех результатов измерений.
выполняется для
всех результатов измерений.
Следующим шагом анализа является проверка гипотезы о нормальности распределения оставшихся результатов измерений. Проверка выполняется по составному критерию, так как количество результатов измерений лежит в диапазоне 10…15<n<40…50.
Применяя первый критерий, следует вычислить отношение:
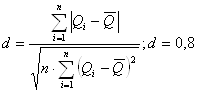
и
сравнить с ![]() и
и
![]() .
.
Задаемся
рекомендуемой доверительной вероятностью ![]() и для уровня значимости
и для уровня значимости ![]() определяем из
соответствующей таблицы квантили распределения
определяем из
соответствующей таблицы квантили распределения ![]() и
и ![]() .
.
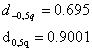
Значение
![]() соответствует
условию
соответствует
условию ![]() .
Первый критерий выполняется.
.
Первый критерий выполняется.
Применяя
второй критерий, задаемся рекомендуемой доверительной вероятностью ![]() и для уровня
значимости
и для уровня
значимости ![]() с
учетом
с
учетом ![]() по
соответствующим таблицам определяем значения
по
соответствующим таблицам определяем значения ![]() и
и ![]() .
.
![]()
Для ![]() из таблицы для
интегральной функции нормированного нормального распределения
из таблицы для
интегральной функции нормированного нормального распределения ![]() определяем значение
определяем значение ![]() и рассчитываем E:
и рассчитываем E:
![]()
![]() ,
, ![]()
Используя правила округления, получим:
![]()
Далее
сравниваем значения ![]() и
и ![]() .
.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
|
|
1,41 | 0,41 | 2,41 | 1,59 | 1,59 | 0,41 | 0,41 | 1,59 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
|
|
1,41 | 1,41 | 1,41 | 0,41 | 2,59 | 3,59 | 2,59 | 0,41 |
| 17 | 18 | 19 | 20 | 21 | 22 | |||
|
|
1,41 | 1,41 | 0,41 | 0,59 | 0,59 | 1,41 |
Мы
видим, что не более m разностей ![]() превосходят
превосходят ![]() , следовательно
второй критерий, а вместе с тем и составной критерий выполняется полностью.
Закон распределения можно признать нормальным с вероятностью
, следовательно
второй критерий, а вместе с тем и составной критерий выполняется полностью.
Закон распределения можно признать нормальным с вероятностью ![]() .
.
Определяем стандартное отклонение среднего арифметического.
Так как закон распределения нормальный, то стандартное отклонение среднего арифметического определяется следующим образом:
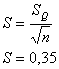
Определяем доверительный интервал
Закон
распределения нормальный, следовательно доверительный интервал для заданной
доверительной вероятности ![]() определяется из распределения
Стьюдента
определяется из распределения
Стьюдента ![]() ,
где
,
где ![]() определяется
из соответствующей таблицы.
определяется
из соответствующей таблицы.
![]()
![]() ,
, ![]()
Используя правила округления, получим:
![]()
Результат измерений запишется в виде:
![]()
Задание 3. Обработка результатов нескольких серий измерений
Условие задания
При
многократных измерениях одной и той же величины получены две серии по 12 (![]() ) результатов
измерений в каждой. Эти результаты после внесения поправок представлены в
таблице. Вычислить результат многократных измерений.
) результатов
измерений в каждой. Эти результаты после внесения поправок представлены в
таблице. Вычислить результат многократных измерений.
Серия измерений 1.
|
|
1 | 2 | 3 | 4 | 5 | 6 |
|
|
485 | 484 | 486 | 482 | 483 | 484 |
|
|
7 | 8 | 9 | 10 | 11 | 12 |
|
|
484 | 481 | 485 | 485 | 485 | 492 |
Серия измерений 2.
|
|
1 | 2 | 3 | 4 | 5 | 6 |
|
|
484 | 481 | 480 | 481 | 484 | 485 |
|
|
7 | 8 | 9 | 10 | 11 | 12 |
|
|
485 | 484 | 483 | 483 | 485 | 492 |
Обработка результатов производится для каждой серии отдельно.
Для
обработки результатов серий измерений необходимо исключить ошибки. Число
измерений лежит в диапазоне 10…15<n<40…50. Поэтому исключение ошибок проводится на основе ![]() критерия.
критерия.
Серия измерений 1.
Определяем среднее арифметическое и среднеквадратическое отклонение результатов серии измерений 1.
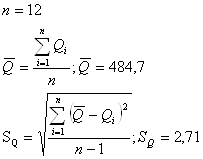
Далее
определяем значения ![]() критерия для каждого значения
результата серии измерений
критерия для каждого значения
результата серии измерений ![]() по формуле:
по формуле:
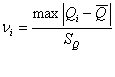
В
соответствии с доверительной вероятностью ![]() с учетом
с учетом ![]() находим из соответствующей
таблицы значение
находим из соответствующей
таблицы значение ![]() , которое зависит от числа
измерений
, которое зависит от числа
измерений ![]() и
и
![]() .
.
![]()
При ![]()
![]() , следовательно,
значение 492 исключаем как ошибку.
, следовательно,
значение 492 исключаем как ошибку.
Исключение
ошибок продолжается до тех пор, пока не будет выполнятся условие ![]() .
.
![]()
|
|
1 | 2 | 3 | 4 | 5 | 6 |
|
|
485 | 484 | 486 | 482 | 483 | 484 |
|
|
7 | 8 | 9 | 10 | 11 | |
|
|
484 | 481 | 485 | 485 | 485 |
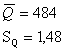
Заново
определяем значения ![]() критерия для каждого значения
результата серии измерений
критерия для каждого значения
результата серии измерений ![]() по формуле:
по формуле:
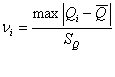
В
соответствии с доверительной вероятностью ![]() с учетом
с учетом ![]() находим из соответствующей
таблицы значение
находим из соответствующей
таблицы значение ![]() , которое зависит от числа
измерений
, которое зависит от числа
измерений ![]() и
и
![]() .
.
![]()
Условие ![]() выполняется
для всех результатов серии измерений.
выполняется
для всех результатов серии измерений.
Следующим шагом анализа является проверка гипотезы о нормальности распределения оставшихся результатов серии измерений. Проверка выполняется по составному критерию, так как количество результатов серии измерений лежит в диапазоне 10…15<n<40…50.
Применяя первый критерий, следует вычислить отношение:

и
сравнить с ![]() и
и
![]() .
.
Задаемся
рекомендуемой доверительной вероятностью ![]() и для уровня значимости
и для уровня значимости ![]() определяем из
соответствующей таблицы квантили распределения
определяем из
соответствующей таблицы квантили распределения ![]() и
и ![]() .
.
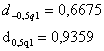
Значение
![]() соответствует
условию
соответствует
условию ![]() .
Первый критерий выполняется.
.
Первый критерий выполняется.
Применяя
второй критерий, задаемся рекомендуемой доверительной вероятностью ![]() и для уровня
значимости
и для уровня
значимости ![]() с
учетом
с
учетом ![]() по
соответствующим таблицам определяем значения
по
соответствующим таблицам определяем значения ![]() и
и ![]() .
.
![]()
Для ![]() из таблицы для
интегральной функции нормированного нормального распределения
из таблицы для
интегральной функции нормированного нормального распределения ![]() определяем значение
определяем значение ![]() и рассчитываем E:
и рассчитываем E:
![]()
![]() ,
, ![]() .
.
Используя правила округления, получим:
![]()
Далее
сравниваем значения ![]() и
и ![]() .
.
|
|
1 | 2 | 3 | 4 | 5 | 6 |
|
|
1 | 0 | 2 | 2 | 1 | 0 |
|
|
7 | 8 | 9 | 10 | 11 | |
|
|
0 | 3 | 1 | 1 | 1 |
Мы
видим, что не более ![]() разностей
разностей![]() превосходят значение
превосходят значение ![]() . Следовательно,
второй критерий, а вместе с тем и составной критерий выполняются полностью.
Закон распределения можно признать нормальным с вероятностью
. Следовательно,
второй критерий, а вместе с тем и составной критерий выполняются полностью.
Закон распределения можно признать нормальным с вероятностью
![]() .
.
Серия измерений 2.
Определяем среднее арифметическое и среднеквадратическое отклонение результатов серии измерений 2.
![]()
|
|
1 | 2 | 3 | 4 | 5 | 6 |
|
|
484 | 481 | 480 | 481 | 484 | 485 |
|
|
7 | 8 | 9 | 10 | 11 | 12 |
|
|
485 | 484 | 483 | 483 | 485 | 492 |
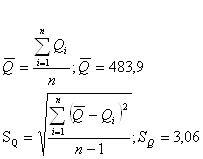
Далее
определяем значения ![]() критерия для каждого значения
результата серии измерений
критерия для каждого значения
результата серии измерений ![]() по формуле:
по формуле:
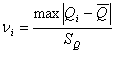
В
соответствии с доверительной вероятностью ![]() с учетом
с учетом ![]() находим из соответствующей
таблицы значение
находим из соответствующей
таблицы значение ![]() , которое зависит от числа
измерений
, которое зависит от числа
измерений ![]() и
и
![]() .
.
![]()
При ![]()
![]() , следовательно значение
492 исключаем как ошибку.
, следовательно значение
492 исключаем как ошибку.
Исключение
ошибок продолжается до тех пор, когда не будет выполнятся условие ![]() .
.
![]()
|
|
1 | 2 | 3 | 4 | 5 | 6 |
|
|
484 | 481 | 480 | 481 | 484 | 485 |
|
|
7 | 8 | 9 | 10 | 11 | |
|
|
485 | 484 | 483 | 483 | 485 |
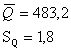
Заново
определяем значения ![]() критерия для каждого значения
результата серии измерений
критерия для каждого значения
результата серии измерений ![]() по формуле:
по формуле:
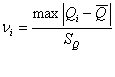
В
соответствии с доверительной вероятностью ![]() с учетом
с учетом ![]() находим из соответствующей
таблицы значение
находим из соответствующей
таблицы значение ![]() , которое зависит от числа
измерений
, которое зависит от числа
измерений ![]() и
и
![]() .
.
![]()
Условие ![]() выполняется
для всех результатов серии измерений.
выполняется
для всех результатов серии измерений.
Следующим шагом анализа является проверка гипотезы о нормальности распределения оставшихся результатов серии измерений. Проверка выполняется по составному критерию, так как количество результатов серии измерений лежит в диапазоне 10…15<n<40…50.
Применяя первый критерий, следует вычислить отношение:
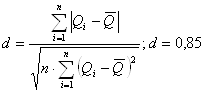
и сравнить
с ![]() и
и ![]() .
.
Задаемся
рекомендуемой доверительной вероятностью ![]() и для уровня значимости
и для уровня значимости ![]() определяем из
соответствующей таблицы квантили распределения
определяем из
соответствующей таблицы квантили распределения ![]() и
и ![]() .
.
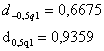
Значение
![]() соответствует
условию
соответствует
условию ![]() .
Первый критерий выполняется.
.
Первый критерий выполняется.
Применяя
второй критерий, задаемся рекомендуемой доверительной вероятностью ![]() и для уровня
значимости
и для уровня
значимости ![]() с
учетом
с
учетом ![]() по
соответствующим таблицам определяем значения
по
соответствующим таблицам определяем значения ![]() и
и ![]() .
.
![]()
Для ![]() из таблицы для
интегральной функции нормированного нормального распределения
из таблицы для
интегральной функции нормированного нормального распределения ![]() определяем значение
определяем значение ![]() и рассчитываем E:
и рассчитываем E:
![]()
![]() ,
, ![]() .
.
Используя правила округления, получим:
![]()
Далее
сравниваем значения ![]() и
и ![]() .
.
|
|
1 | 2 | 3 | 4 | 5 | 6 |
|
|
0,82 | 2,18 | 3,18 | 2,18 | 0,82 | 1,82 |
|
|
7 | 8 | 9 | 10 | 11 | |
|
|
1,82 | 0,82 | 0,18 | 0,18 | 1,82 |
Мы
видим, что не более ![]() разностей
разностей ![]() превосходят значение
превосходят значение ![]() . Следовательно
второй критерий, а вместе с тем и составной критерий выполняется полностью.
Закон распределения можно признать нормальным с вероятностью
. Следовательно
второй критерий, а вместе с тем и составной критерий выполняется полностью.
Закон распределения можно признать нормальным с вероятностью ![]() .
.
Далее необходимо проверить значимость различия средних арифметических серий.
Для этого необходимо вычислить моменты закона распределения разности:

Задавшись
доверительной вероятностью ![]() , определяем из соответствующих
таблиц интегральной функции нормированного нормального распределения
, определяем из соответствующих
таблиц интегральной функции нормированного нормального распределения ![]() значение
значение ![]() и сравниваем
и сравниваем ![]() с
с ![]() .
.
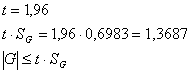
Условие ![]() выполняется.
Различие между средними арифметическими в сериях с доверительной вероятностью
выполняется.
Различие между средними арифметическими в сериях с доверительной вероятностью ![]() можно признать
незначимым.
можно признать
незначимым.
Далее необходимо проверить равнорассеянность результатов измерений в сериях.
Для этого определяем значение:
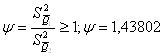
И,
задавшись доверительной вероятностью ![]() , определяем из соответствующих
таблиц значение аргумента интегральной функции распределения вероятности Фишера
, определяем из соответствующих
таблиц значение аргумента интегральной функции распределения вероятности Фишера
![]() .
.
![]()
Условие ![]() выполняется.
Серии с доверительной вероятностью
выполняется.
Серии с доверительной вероятностью ![]() считаем рассеянными.
считаем рассеянными.
Выше
было показано, что серии равнорассеяны и с незначимым различием средних
арифметических. Исходя из этого все результаты измерений объединяются в единый
массив и затем для него выполняется обработка по алгоритму, согласно которому
необходимо определить оценку результата измерения ![]() и среднеквадратического
отклонения
и среднеквадратического
отклонения ![]() .
.
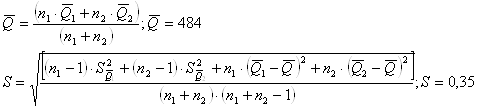
Задавшись
доверительной вероятностью ![]() , определяем из таблиц
распределения Стьюдента значение
, определяем из таблиц
распределения Стьюдента значение ![]() для числа степеней свободы
для числа степеней свободы
![]()
Затем
определяем доверительный интервал ![]() :
:
![]()
![]()
Используя правила округления, получим:
![]()
Результат измерений запишется в виде:
![]() .
.
Задание 4. Функциональные преобразования результатов измерений (косвенные измерения)
Условие задания
При
многократных измерениях независимых величин ![]() и
и ![]() получено по 12 (n) результатов измерений. Эти
результаты после внесения поправок представлены в таблице 2. Определить
результат вычисления
получено по 12 (n) результатов измерений. Эти
результаты после внесения поправок представлены в таблице 2. Определить
результат вычисления ![]() , (вид функции
, (вид функции ![]() и характер величин
и характер величин ![]() представлены в
таблице 3).
представлены в
таблице 3).
Вид
функциональной зависимости ![]() .
.
Характер и единицы величин:
![]() - ЭДС, мВ;
- ЭДС, мВ;
![]() -
сопротивление, Ом;
-
сопротивление, Ом;
![]() - сила тока,
А.
- сила тока,
А.
Обработка
результатов измерений величин ![]() и
и ![]() проведена в задании 3 первой
расчетно-графической работы.
проведена в задании 3 первой
расчетно-графической работы.
Средние
значения и среднеквадратические отклонения для величин ![]() и
и ![]() имеют вид
имеют вид
![]()
![]()
Гипотеза
о нормальности распределения величин ![]() и
и ![]() подтверждается.
подтверждается.
Определим оценку среднего значения функции:
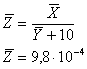
Определим поправку
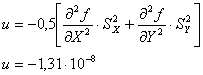
Определим оценку стандартного отклонения функции
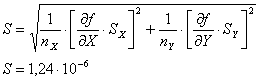
Определяем доверительный интервал для функции
![]()
Законы
распределения вероятности результатов измерения ![]() и
и ![]() признаны нормальными,
признаны нормальными, ![]() можно
определить для принятой доверительной вероятности
можно
определить для принятой доверительной вероятности ![]() из таблиц для распределения
Стьюдента. При этом число степеней свободы
из таблиц для распределения
Стьюдента. При этом число степеней свободы ![]() определяется из выражения
определяется из выражения
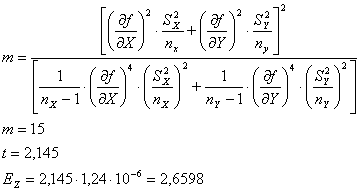
Используя правила округления, получим:
![]()
Результат запишется в виде:
![]()
Задание 5. Обработка экспериментальных данных при изучении зависимостей
Условие задания
При
многократных совместных измерениях величин ![]() и
и ![]() получено по 20 (n) пар результатов измерений. Эти результаты после внесения
поправок представлены в таблице 4. Определить уравнение регрессии
получено по 20 (n) пар результатов измерений. Эти результаты после внесения
поправок представлены в таблице 4. Определить уравнение регрессии ![]() по
по ![]() :
: ![]() .
.
|
|
1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
|
61;602 | 62;613 | 63;620 | 64;631 | 65;639 | 66;648 | 67;656 |
|
|
8 | 9 | 10 | 11 | 12 | 13 | 14 |
|
|
68;662 | 69;667 | 70;682 | 9;87 | 19;188 | 29;286 | 39;386 |
|
|
15 | 16 | 17 | 18 | 19 | 20 | |
|
|
49;485 | 59;575 | 69;667 | 79;770 | 89;868 | 99;966 |
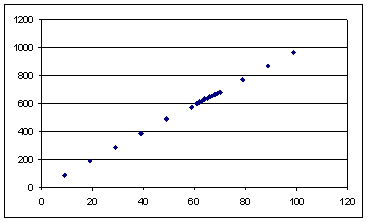
В качестве прямой регрессии будем использовать прямую вида
![]() .
.
Параметры прямой определим по методу наименьших квадратов.

Далее проверяем правильность выбора вида уравнения регрессии. Для этого следует применить критерии серий и инверсий.
Рассчитываем отклонения экспериментальных значений от соответствующих расчетных значений, рассчитанных для того же аргумента:
![]()
|
|
1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
|
-4,67 | -0,67 | 0,33 | 3,33 | 5,33 | -1,67 | 5,93 |
|
|
8 | 9 | 10 | 11 | 12 | 13 | 14 |
|
|
7,23 | 4,53 | 5,83 | 4,13 | 3,43 | 1,73 | -1,97 |
|
|
15 | 16 | 17 | 18 | 19 | 20 | |
|
|
-6,67 | -6,67 | -1,37 | -0,67 | 0,33 | 1,33 |
последовательность ∆Yi записана по мере возрастания Х
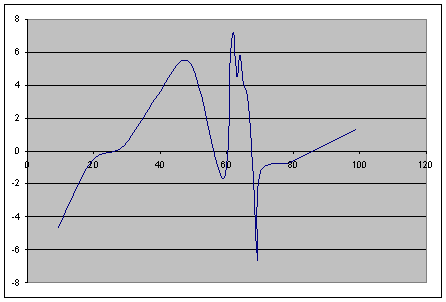
Критерий серий:
Рассчитываем число серий в полученной последовательности: N=6
Задавшись
доверительной вероятностью ![]()
![]() , для n=20 определяем по таблице допустимые границы
, для n=20 определяем по таблице допустимые границы ![]() и
и ![]() :
:
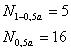
Критерий инверсий:
Рассчитываем
число инверсий А в полученной последовательности ![]() : А=106.
: А=106.
Задавшись
доверительной вероятностью ![]()
![]() для n=20 определяем по таблице допустимые границы
для n=20 определяем по таблице допустимые границы ![]() и
и ![]() :
:
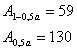
Оба
неравенства выполняются ![]() и
и ![]() . Поэтому можно считать, что
рассчитанное уравнение регрессии достоверно описывает экспериментально
исследуемую зависимость.
. Поэтому можно считать, что
рассчитанное уравнение регрессии достоверно описывает экспериментально
исследуемую зависимость.