Курсовая работа: Исследование систем автоматического управления (САУ)
Курсовая работа
По курсу «Теория автоматического управления»
На тему: «Исследование систем автоматического управления (САУ)»
Задание. 1 вариант
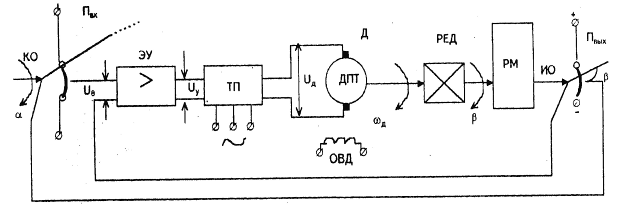
Рис.1 Принципиальная схема САУ
Табл. 1.
| С1, с | Тм, с | Тэ, с | Ттп, с | Кред, | Кд, Рад/Вс | Ктп, | Кэу | Кпот, В/рад |
| 0,04 | 0,833 | 0,02 | 3,33×10-3 | 1/350 | 2,5 | 20 | 35 | 70 |
Обозначения, принятые в таблице 1:
Тэ, Тм - соответственно электромагнитная и электромеханическая постоянная времени двигателя;
Ттп - постоянная времени тиристорного преобразователя;
kред, kд, kтп, kэу, kпот - коэффициенты усиления соответственно редуктора, двигателя Д, тиристорного преобразователя, электронного усилителя, потенциометра.
Значения коэффициентов С2 и СЗ соответственно равны: 0,1 с2 и – 0,15 с3.
1. Основные свойства и функциональное назначение элементов, образующих САУ. Принцип действия САУ
1.1 Основные свойства и функциональное назначение элементов САУ
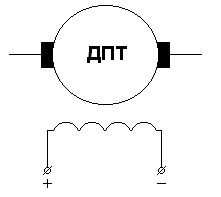
1.1.1 Двигатель постоянного тока
Двигатель постоянного тока имеет обмотку возбуждения, расположенную на явно выраженных полюсах статора. По обмотке возбуждения проходит постоянный ток, который создает магнитное поле возбуждения. В двигателе размещена двухслойная обмотка, в которой при вращении якоря индуктируется ЭДС. При заданном направлении вращения ЭДС, которое индуктируется в проводниках, зависит только от того, под каким полюсом находится проводник.
Потенциометрическое измерительное устройство
![]()
![]()
![]()
![]()
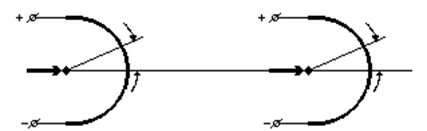
Разновидностью информационных электрических микромашин, предназначенных для использования в дистанционных системах передачи угла, является потенциометрическое измерительное устройство. Выходным сигналом (управляемой величиной) является угол поворота вала рабочего механизма b или, что то же самое, угол поворота движка потенциометра Пвых, поскольку этот потенциометр расположен на одном валу с рабочим механизмом (на исполнительной оси ИО), а выходным сигналом – угол поворота a движка потенциометра Пвх, который расположен на командной оси КО.
Алгоритм функционирования рассматриваемого привода заключается в том, чтобы исполнительная ось ИО следила бы за произвольно изменяющимся положением оси КО, т. е. b ( t ) = a (t) при действии на элементы системы различных возмущений, в частности момента статического сопротивления Мс.
Измерительное устройство системы (потенциометры Пвх и Пвых) определяет угловое рассогласование e(t) между заданным значением угла поворота командной оси a(t) и действительным значением управляемой величины – углом поворота исполнительной оси b(t) и преобразует сигнал
e(t) = a(t) - b(t)
в пропорциональное ему напряжения рассогласования Ue(t), т. е.
Ue(t) = Ua(t) - Ub(t) = Ke[ a(t) - b(t) ] - Ke × e(t)
где Ua , Ub – соответственно потенциалы движков потенциометров Пвх и Пвых ; Кe – коэффициент усиления измерительного устройства (потенциометры Пвх и Пвых имеют одинаковые конструкции и параметры). Затем сигнал Ue (t) усиливается по напряжению и мощности соответственно с помощью УТП и ТП. В результате на выходе регулятора формируется управляющее воздействие – напряжение Uд(t) , которое подводится к якорной обмотке двигателя. Значение управляющего напряжения зависит от величины сигнала рассогласования коэффициентов усиления тиристорного преобразователя Кт.п – и усилителя постоянного тока Купт.
1.1.3 Электронный усилитель
Электронный усилитель – устройство, предназначенное для повышения мощности входного электрического сигнала. При этом усиление маломощного входного сигнала достигается за счет энергии внешнего источника питания значительно большего уровня мощности. Структурная схема усилителя показана в виде активного четырёхполюсника, к входным зажимам которого подключается источник входного сигнала в виде источника напряжения. Сопротивление нагрузки Rн подключается к выходным зажимам.
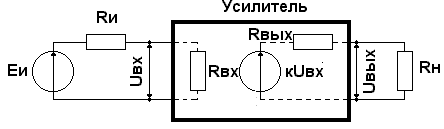
Усилитель содержит активные (полупроводниковые приборы) и пассивные (резисторы, конденсаторы, индуктивности) элементы, а также источники питания. Пассивные элементы предназначены для обеспечения заданного режима работы активных элементов.
1.1.4 Тиристорный преобразователь
Тиристорный преобразователь состоит из системы импульсно-фазового управления (СИФУ) и собственно тиристорного преобразователя, основным элементом которого является силовая схема преобразования энергии переменного тока в энергию постоянного тока (управляемый выпрямитель) с помощью тиристоров.
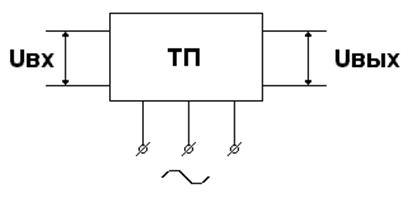
В качестве нагрузки преобразователя принята якорная цепь двигателя постоянного тока. СИФУ осуществляет преобразование непрерывного сигнала управления Uу(t), поступающего на его вход, в последовательность отпирающих импульсов ai(t) (формируемых генератором импульсов), сдвинутых по фазе относительно момента естественного отпирания тиристоров. Затем с помощью собственно тиристорного преобразователя производится обратное преобразование дискретных значений ai(t) в кусочно-непрерывный сигнал выходной координаты – ЭДС преобразователя.
1.1.5 Редуктор
Представляет собой сугубо механическую конструкцию, предназначенную для передачи вращающего момента, уменьшения (увеличения) частоты вращения вала.
Состоит из зубчатой передачи любого типа (выбирается в зависимости от конкретных нужд и прикладываемых сил). Могут быть одно — и несколько - ступенчатыми, различными по форме, назначению, методам охлаждения и т.п.
Принцип действия САУ
Рассмотрим работу следящего привода. При идентичном положении командной и исполнительной осей привода угол рассогласования между ними равен нулю. Также равны нулю напряжения Ue и Uд , т. е. двигатель и вся система находятся в покое. Повернем теперь командную ось на некоторый угол. В результате этого возникнут угол рассогласования e = a - b и пропорциональные ему напряжения Uд двигатель вращаться и через редуктор будет поворачивать исполнительную ось и движок потенциометра Пвых в сторону уменьшения угла рассогласования до тех пор, пока этот угол не станет равным нулю. При повороте командной оси в другую сторону меняется полярность напряжения, прикладываемого к двигателю, и, следовательно, направления его вращения. Если угловое напряжение a(t) командной оси изменяется во времени по произвольному закону, то и угловое положение b(t) исполнительной оси также будет изменятся по тому же закону.
Следует отметить, что направление вращения двигателя будет совпадать со знаком угла рассогласования только в том случаи, когда обратная связь от двигателя к исполнительной оси (движку потенциометра Пвых) будет отрицательной. Если же при вращении двигателя угол рассогласования возрастёт, то это означает, что обратная связь положительна. Для того чтобы сделать её отрицательной, необходимо поменять полярность напряжения, прикладываемого к двигателю.
Функциональная схема САУ приведена ниже по тексту (см. рис. 2).

Рис.2 Функциональная схема САУ
2. Дифференциальные управления и передаточные функции элементов, образующих САУ
2.1 Потенциометр
Потенциометрическое устройство описывается уравнением:
Uq(t) = kпот × q (t),
где kпот=70 в/рад.
Уравнение потенциометра в операционной форме:
Uq(S) = kпот × q (S).
Откуда передаточная функция потенциометра:
Wпот(S) = 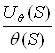 = kпот.
= kпот.
Следовательно, потенциометрическое устройство представлено пропорциональным звеном и описываются уравнением:
Uq(S) = 70×q (S).
2.2 Тиристорный преобразователь
Тиристорный преобразователь в режиме непрерывного тока описывается звеном, состоящим из последовательного соединения линейного безинерционного звена с коэффициентом усиления kтп и звена чистого запаздывания, то есть
![]() ,
,
где t – случайное время, обычно называемое среднестатистическим запаздыванием.
Обычно функция ![]() раскладывается в степенной ряд и
учитываются только два первых члена этого ряда. Тогда передаточная функция
тиристорного преобразователя принимает вид:
раскладывается в степенной ряд и
учитываются только два первых члена этого ряда. Тогда передаточная функция
тиристорного преобразователя принимает вид:
![]() .
.
Учитывая, что Ттп = t получаем
![]() ,
,
где Ттп = 3.33×10-3![]() с, kтп = 20.
с, kтп = 20.
Для данной передаточной функции дифферинциальное уравнение:
![]()
2.3 Электронный усилитель
Электронный усилитель описывается уравнением:
Uу(t) = kэу × Uq (t),
где kэу = 35.
Уравнение электронного усилителя в операционной форме:
Uу(S) = kэу × Uq (S).
Откуда передаточная функция электронного усилителя:
Wэу(S) = 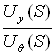 = kэу.
= kэу.
Следовательно, электронный усилитель представлен пропорциональным звеном и описываются уравнением:
Uу(S) = 35×Uq (S).
2.4 Двигатель постоянного тока
Рассмотрим участок системы, включающей ТП и двигатель. Входной величиной этого участка является Uд(t), а выходной — угловая скорость w(t) двигателя.
Найдем уравнение, связывающее w(t) и Uд(t).
Уравнение Uд(t) в электрической цепи, состоящей из ТП и обмотки якоря двигателя, имеет вид:
Uд(t) = ![]() , <1>
, <1>
где Rd – активное сопротивление обмоток и щеток двигателя;
Ld – индуктивность щеток;
eд(t) = ![]()
- противо ЭДС двигателя.
Можно считать, что магнитный поток двигателя Ф = const,
тогда:
eд(t) = ![]() ;
; ![]() ; <2>
; <2>
Подставляя <2> в <1> получим:
Uд(t) = ![]() <3>
<3>
Формула <3> - уравнение Uд(t) в рассматриваемой цепи. Однако в этой цепи есть и механическая энергия, поэтому необходимо составить уравнение моментов:
Mвр = ![]() ; <4>
; <4>
где J – момент инерции всех вращающихся частей, приведенных к валу двигателя, Нмс2;
Mc – приведенный момент сопротивления рабочего механизма.
Момент вращения двигателя
Mвр = ![]()
или учитывая, что Ф = const,
Mвр = ![]() ;
; ![]() .
.
Подставив Mвр в уравнение моментов, получим:
![]() =
= ![]() ; <5>
; <5>
Примем MC = 0, тогда
![]() =
= ![]() ; <6>
; <6>
Находим i из <6> и подставляем его в уравнение <3>:
Uд(t) =  <7>
<7>
или
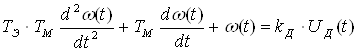 ; <8>
; <8>
где
![]()
- электромагнитная постоянная времени цепи;

- электромеханическая постоянная времени цепи;
![]() .
.
Характер переходной функции двигателя зависит от значений Тэ и Тм. Так как Тм = 0.833 с, Тэ = 0.02 с, то
![]() .
.
Тогда при ![]() получим
получим
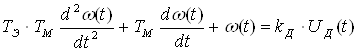 <9>
<9>
Запишем <9> в операционной форме:
![]() <10>
<10>
откуда передаточная функция рассматриваемого участка:
Wд(S) = 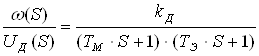 . <11>
. <11>
Полученная передаточная функция соответствует передаточной функции апериодических звеньев.
2.5 Редуктор
Угол поворота приемного вала определяется соотношением:
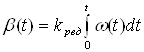 .
.
Запишем это уравнение в операционной форме:
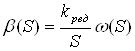 .
.
Передаточная функция звена:
Wред(S) = 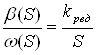 .
.
Следовательно, динамической моделью редуктора является интегрирующее звено.
3. Дифференциальные уравнения и передаточные функции САУ
3.1 Структурная схема САУ
Структурная схема САУ представляет собой графическое изображение математической модели системы и отражает ее динамические свойства. Для получения структурной схемы САУ необходимо заменить временные уравнения на их изображения, представленных в операторном виде.
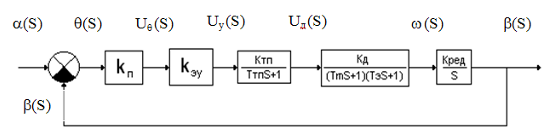
Рис.3 Структурная схема САУ
В приведенной на рис.3 системе нет местных обратных связей, и поэтому имеется только один замкнутый контур, образованный с помощью главной отрицательной обратной связи.
3.2 Дифференциальное уравнение и передаточная функция разомкнутой САУ
Размыкаем схему на рис.3 перед элементом сравнения (цепь обратной связи) и разворачиваем в прямую цепь. Для разомкнутой САУ входной величиной является угол рассогласования q(t), а выходной величиной - угол поворота b(t) вала рабочего механизма.
Передаточная функция разомкнутой САУ представляет собой произведение передаточных функций каждого звена:
Wр(S) = ![]() ,
,
где коэффициент усиления разомкнутой САУ kv определяется как произведение:
kv = kпот×kред×kтп×kэу×kд = 70×35×20×2,5×1/350 = 350.
Тогда передаточная функция разомкнутой САУ примет вид:
Wр(S) = ![]() .
.
Для данной передаточной функции разомкнутой САУ получим следующее дифференциальное уравнение:

3.3 Дифференциальное уравнение и передаточная функция замкнутой САУ
Замыкаем цепь обратной связи. Для замкнутой системы входной величиной является угол поворота входного вала a(t), а выходной - угол поворота b(t). В замкнутом состоянии величина q(t) представляет собой рассогласование:
q(t) = a(t) - b(t).
Передаточную функцию замкнутой САУ можно определить следующим образом:
![]()
3.4 Дифференциальное уравнение и передаточная функция ошибки. Исследование САУ на астатизм
Ошибка q(t) характеризует точность воспроизведения следящей системой входной величины. В качестве входной величины следует принять угол поворота a(t), а выходной - угол рассогласования q(t).
Уравнению ошибки соответствует передаточная функция:
![]()
Исследуем САУ на астатизм по полученной передаточной функции ошибки:
А) определяем С0:
![]() .
.
так как С0 = 0, то эта система астатическая;
Б) определяем С1:
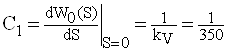
так как ![]() , то система является астатической
первого порядка.
, то система является астатической
первого порядка.
4. Исследование устойчивости исходной замкнутой САУ
4.1 Исследование устойчивости САУ по критерию Гурвица
Критерием, пригодным для оценки устойчивости уравнений порядка выше третьего, является критерий немецкого математика Гурвица. Составим характеристическое уравнение исходной замкнутой САУ:
![]()
Обозначим
![]() ;
;
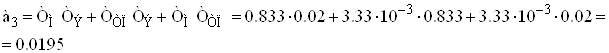
![]() ;
;
![]() ;
;
![]() .
.
Составим определитель Гурвица по определению:
 ;
;
Составим диагональные миноры:
![]() ;
;
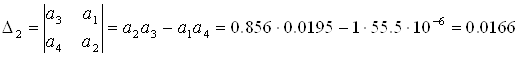 ;
;
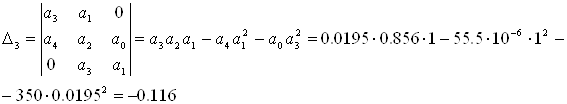
Итак, получаем, что ![]() ;
; ![]() ;
; ![]() , т.е. условие устойчивости
системы не выполняется, а следовательно система по критерию Гурвица
неустойчива.
, т.е. условие устойчивости
системы не выполняется, а следовательно система по критерию Гурвица
неустойчива.
4.2 Исследование устойчивости САУ по критерию Найквиста
В соответствии со структурной схемой (рис.3) АЧХ и ФЧХ разомкнутой САУ можно представить в виде произведения АЧХ и суммы ФЧХ элементарных динамических звеньев:
а) интегрирующего звена:
![]() ,
,![]() ;
;
б) апериодического звена первого порядка:
![]() ,
,![]() ;
;
в) апериодического звена первого порядка:
![]() ,
,![]() ;
;
г) апериодического звена первого порядка:
![]() ,
,![]() ;
;
Задаемся определенным значением частоты и определяем АЧХ и ФЧХ для каждого звена. Результаты вычислений сведены в табл.2. Причем
A (w) = A1(w)A2(w)A3(w)A4(w);
j(w) = j1(w)+j2(w)+j3(w)+j4(w).
По данным табл.2 строим АФЧХ исходной разомкнутой САУ. Снимая показания, видим, что график при пересечении отрицательной вещественной оси охватывает точку с координатами (-1;j0). Следовательно исходная система неустойчива.
Табл. 2
| Звенья | w,с-1 | |||||||||
| 0 | 2 | 5 | 10 | 20 | 50 | 100 | 150 | 200 | ||
| W1(jw) | A1(w) | ¥ | 175 | 70 | 35 | 17,5 | 7 | 3,5 | 2,3 | 1,75 |
| j1(w) | -90 | -90 | -90 | -90 | -90 | -90 | -90 | -90 | -90 | |
| W2(jw) | A2(w) | 1 | 1 | 0,999 | 0,999 | 0,998 | 0,986 | 0,949 | 0,895 | 0,832 |
| j2(w) | 0 | -0,38 | -0,95 | -1,91 | -3,81 | -9,45 | -18,4 | -26,5 | -33,7 | |
| W3(jw) | A3(w) | 1 | 0,51 | 0,23 | 0,12 | 0,06 | 0,02 | 0,012 | 0,008 | 0,006 |
| j3(w) | 0 | -59 | -76,5 | -83,2 | -86,6 | -88,6 | -89,3 | -89,5 | -89,7 | |
| W4(jw) | A4(w) | 1 | 0,999 | 0,995 | 0,981 | 0,928 | 0,707 | 0,447 | 0,316 | 0,243 |
| j4(w) | 0 | -2,3 | -5,7 | -11,3 | -21,8 | -45 | -63,4 | -71,6 | -76 | |
| A(w) | ¥ | 89,2 | 16 | 4,12 | 0,97 | 0,1 | 0,02 | 0,005 | 0 | |
| j(w) | -90 | -152 | -173 | -186 | -202 | -233 | -261 | -277 | -289 |
4.3 Исследование устойчивости САУ по логарифмическому критерию
Для исследования САУ по логарифмическому критерию строим логарифмические амплитудно-частотную (ЛАЧХ) и фазочастотную (ЛФЧХ) характеристики разомкнутой САУ. Для этого определяем частоты сопряжения
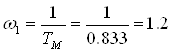 с-1;
с-1;
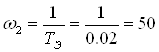 с-1;
с-1;
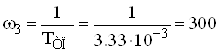 с-1;
с-1;
коэффициент усиления САУ
![]() дб.
дб.
наклон первой асимптоты — -20 дб/дек;
наклон второй изменяется на -20дб/дек и составляет — -40 дб/дек;
наклон третьей изменяется на -20 дб/дек и составляет — -60 дб/дек;
наклон четвёртой изменяется на -20 дб/дек и составляет — -80 дб/дек;
Для построения ЛФЧХ используем данные табл. 2. Из характеристик очевидно, что система неустойчива, так как ЛФЧХ пересекает ось w раньше, чем ЛАЧХ.
4.4 Сопоставление результатов исследования устойчивости различными методами
Рассмотренные выше критерии устойчивости дали один и тот же результат. Однако, с точки зрения практического использования они неравноценны.
Критерий Гурвица позволяет получить только качественное суждение о характере процесса регулирования, т.е. устойчивость, устойчив или нет процесс; но он является наиболее точным. А также данный метод позволяет определить предельный коэффициент усиления САУ.
Частотный критерий Найквиста применяется тогда, когда трудно получить уравнения всех звеньев, но можно получить экспериментально - фазовые их характеристики. Устойчивость по данному методу определяется по тому, как АФЧХ охватывает точку с координатами (-1; j0).
Кроме того, расположение ЛФЧХ еще не дает прямого ответа, устойчива ли система, что требует дополнительных исследований.
При использовании логарифмических частотных характеристик оценка устойчивости системы производится проще, т.е. по их виду можно заключить, устойчива система или нет; но можно получить противоречивые показания, так как мы используем приближенную ЛАЧХ, вместо точной.
5. Синтез последовательного корректирующего устройства
5.1 Расчет и построение желаемой логарифмической частотной характеристики
Синтез последовательного корректирующего устройства выполним методом логарифмических характеристик.
В дальнейшем будем предполагать, что САУ состоит из измерительного устройства, исполнительного устройства и объекта управления с общей передаточной функцией W(S) и последовательного корректирующего устройства с передаточной функцией Wку(S).
При рассмотрении желаемой логарифмической частотной характеристики (ЖЛАЧХ) выделим четыре области:
а) область очень низких частот (0, ![]() ).
).
Наклон характеристики составляет — -20 дб/дек, по количеству интегрирующих звеньев;
б) область низких частот ( ![]() ,
,![]() ).
).
Наклон составляет - 40 дб/дек, по количеству апериодических звеньев с постоянной времени
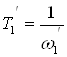 ;
;
в) область средних частот (![]() ,
,![]() ).
).
Наклон на частоте среза ![]() составляет – 20 дб/дек для
обеспечения необходимых запасов устойчивости.
составляет – 20 дб/дек для
обеспечения необходимых запасов устойчивости.
г) область высоких частот (![]() ,¥ ).
,¥ ).
Наклон существенно не влияет на качество САУ, поэтому выберем его по исходной ЛАЧХ.
Рассчитаем параметры ЖЛАЧХ:
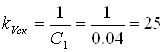 ;
; ![]() дб.
дб.
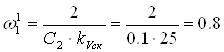 с-1
с-1
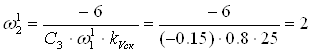 с-1
с-1
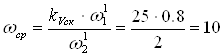 с-1
с-1
По полученным данным и с учётом предъявляемых требований строим ЖЛАЧХ.
5.2 Выбор последовательного корректирующего устройства и расчет его параметров
Решим задачу синтеза последовательного корректирующего устройства. Для этого из ЖЛАЧХ геометрически вычтем ЛАЧХ не скорректированной системы. Полученная характеристика представляет собой ЛАЧХ корректирующего устройства.
По виду ЛАЧХ корректирующего устройства определим его передаточную функцию, схему и параметры. Приведенной ЛАЧХ корректирующего устройства соответствует ниже представленная схема:
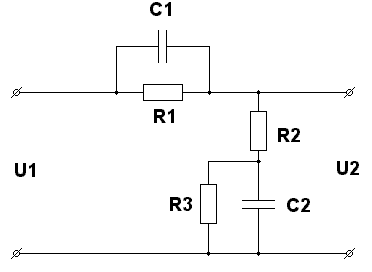
Рис. 4 Схема корректирующего устройства
![]() ;
; ![]() .
.
Передаточная функция устройства:
Wск(S) = 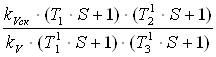 ;
;
где ![]() с;
с; ![]() с;
с; ![]() с;
с; ![]() с;
с;
kVск – коэффициент усиления скорректированной САУ;
kV – коэффициент усиления исходной САУ.
Количество сомножителей вида (![]() ) в числителе соответствует
количеству переходов +20дб/дек, а в знаменателе — -20дб/дек. Постоянные времени
) в числителе соответствует
количеству переходов +20дб/дек, а в знаменателе — -20дб/дек. Постоянные времени
![]() ,
определяются соответствующими частотами сопряжения на ЛАЧХ корректирующего
устройства.
,
определяются соответствующими частотами сопряжения на ЛАЧХ корректирующего
устройства.
Рассчитаем параметры корректирующего устройства:
примем ![]() мФ, тогда
мФ, тогда
![]() Ом;
Ом;
примем![]() Ом, тогда
Ом, тогда
![]() мФ.
мФ.
Структурную схему скорректированной САУ можно представить в виде:

Рис. 5 Структурную схему скорректированной САУ
6. Расчет и построение переходной характеристики скорректированной САУ
6.1 Расчет фазовой частотной характеристики скорректированной САУ
Расчет ФЧХ скорректированной САУ произведем по звеньям
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
а результаты занесем в табл.3. По рассчитанным данным построим ЛФЧХ скорректированной САУ. Из характеристик, очевидно, что система устойчива.
Запас по фазе – 57,5°, по амплитуде – 12 дб.
Табл. 3
| Звенья | w,с-1 | ||||||||
| 0 | 2 | 5 | 10 | 20 | 50 | 100 | 150 | 200 | |
| jа1(w) | 0 | -68,2 | -80,9 | -85,4 | -87,7 | -89,1 | -89,5 | -89,7 | -89,8 |
| jа2(w) | 0 | -2,6 | -6,56 | -12,95 | -24,7 | -49,0 | -66,5 | -73,8 | -77,7 |
| jф1(w) | 0 | 58,9 | 76,5 | 83,1 | 86,6 | 88,6 | 89,3 | 89,5 | 89,65 |
| jф2(w) | 0 | 45,0 | 68,2 | 78,7 | 84,3 | 87,7 | 88,85 | 89,2 | 89,4 |
| jåж(w) | 0 | 33,1 | 57,2 | 63,45 | 58,5 | 38,2 | 22,15 | 15,2 | 11,55 |
| jå(w) | -90 | -118,6 | -116 | -123 | -143,7 | -194,9 | -239 | -262,4 | -277,9 |
7. Определение показателей качества замкнутой скорректированной САУ
По построенной переходной характеристике
скорректированной системы, определяем основные показатели качества:
перерегулирование ![]() , время первого согласования
, время первого согласования ![]() , время
достижения первого максимума
, время
достижения первого максимума ![]() , время регулирования
, время регулирования ![]() , число
колебаний N, а также запасы по фазе и амплитуды:
, число
колебаний N, а также запасы по фазе и амплитуды:
![]() с,
с,
![]() с,
с,
![]() с,
с,
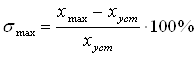 ;
;
![]() ,
,
Азап = 12 дБ,
jзап = 57,50.