Курсовая работа: Кинематический и силовой анализ механизмов иглы и нитепритягивателя универсальной швейной машины
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
КГТУ
кафедра «дизайн и технология изделий легкой промышленности»
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
К курсовому проекту по дисциплине «Оборудование для швейного производства и основы проектирования оборудования»
на тему «Кинематический и силовой анализ механизмов иглы и нитепритягивателя универсальной швейной машины»
Автор проекта Горбункова М.В.
(подпись, дата) (инициалы, фамилия)
Специальность 260901 «Технология швейных изделий»
(номер, наименование)
Обозначение курсового проекта КП 2068448-260901-03-07 Группа ТШ-51
![]()
![]() Руководитель проекта
Ноздрачева Т.М.
Руководитель проекта
Ноздрачева Т.М.
(подпись, дата) (инициалы, фамилия)
Работа защищена Оценка
Члены комиссии__________________________ Данилова С. А.
Курск 2007
ЗАДАНИЕ
на курсовой проект по дисциплине
«Оборудование для швейного производства и основы проектирования оборудования»
Студентка кафедры «Дизайна и технологии изделий легкой промышленности» III курса ТШ-51 группы
Горбункова Марина Владимировна
(фамилия, имя, отчество)
Тема проекта «Кинематический и силовой анализ механизмов иглы и нитепритягивателя универсальной швейной машины»
Исходные данные кинематическая схема механизмов иглы и нитепритягивателя швейной машины 1022 класса; частота вращения главного вала машины – 4800 мин-1; координаты Х и У неподвижного шарнира О2 соединительного звена нитепритягивателя – 18, 26; размеры звеньев механизмов иглы и нитепритягивателя: О1А-14 мм, О1С-12 мм, АС-9 мм, АВ-35 мм, О2Д-24 мм, СД-24 мм, ДЕ-31 мм, СЕ-51 мм; сила полезного сопротивления – 80 сН; масса звеньев механизма иглы: кривошип – 0,019 кГ, шатун – 0,19 кГ, ползун – 0,03 кГ.
Основные вопросы, подлежащие разработке:
Введение
Построение кинематических схем и разметка траекторий.
Расчет скоростей звеньев механизма и отдельных точек, построение плана скоростей.
Расчет ускорений звеньев механизма и отдельных точек, построение планов ускорений.
Силовой анализ механизма иглы. Построение планов сил.
Заключение
Перечень материалов, предоставляемых к защите:
Пояснительная записка 15-20 листов
Графическая часть на 1 листе формата А1
Срок предоставления к защите__________________________
Руководитель проекта Ноздрачева Т.М____________
Задание к исполнению принял___________________________
СОДЕРЖАНИЕ
Введение
1. Построение кинематической схемы и траекторий рабочих точек механизмов иглы и нитепритягивателя
2.Определение скоростей звеньев механизмов иглы и нитепритягивателя
3.Определениеускорений звеньев механизмов иглы и нитепритягивателя и построение плана ускорений
4.Силовой анализ механизмов
Заключение
Список используемой литературы
Приложения
ВВЕДЕНИЕ
Целью курсового проекта является обобщение, углубление и закрепление знаний, полученных мною на лекциях и при выполнении лабораторных работ по дисциплине «Оборудование для швейного производства и основы проектирования оборудования», и их применение при решении технических, технологических, научных и экономических задач, возникающих при проектировании швейного оборудования.
В процессе работы должна ознакомиться с основными этапами проектирования швейного оборудования, глубоко изучить технологический процесс, осуществляемый на универсальной швейной машине, научиться составлять и анализировать кинематические схемы исполнительных механизмов. Также я должна освоить методику проведения перемещений, скоростей, ускорений звеньев механизмов и их отдельных точек, научиться устанавливать законы изменения во времени этих величин, определять силы, действующие на звенья механизмов, реакции в кинематических парах и давления на станину машины. Таким образом, я должна научиться решать задачи кинематического и динамического анализа механизмов, необходимого для выполнения расчетов проектируемого швейного оборудования.
При выполнении курсового проекта нужно учитывать основные задачи, стоящие перед швейной промышленностью по техническому перевооружению производства, применению современных средств механизации и автоматизации оборудования, созданию конкурентоспособного оборудования, экономному использованию материальных и трудовых ресурсов.
1 Построение кинематической схемы и траекторий рабочих точек механизмов иглы и нитепритягивателя
Под кинематической схемой понимают изображение механизма, машины или установки, на котором должна быть представлена вся совокупность кинематических элементов и их соединений, предназначенных для осуществления регулирования, управления и контроля заданных движений исполнительных органов.
|
|
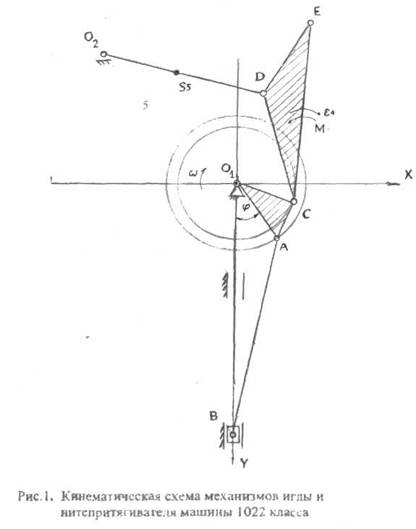
Кинематическая схема может быть плоской или пространственной (в ортогональном или аксонометрическом изображении). На рис. I представлена плоская кинематическая схема механизмов иглы и нитепритягивателя универсальной швейной машины 1022 класса. На рис. 2 - пространственная конструктивно-кинематическая схема.
Машина 1022 класса предназначена для стачивания деталей швейных изделий из хлопчатобумажных и шерстяных тканей однолинейной двухниточной строчкой челночного переплетения. Основными рабочими механизмами машины являются: кривошипно-шатунный механизм иглы, ротационный механизм челнока, шарнирно-стержневой механизм нитепритягивателя, простой механизм транспортирования материалов, узел лапки. В машине осуществляется централизованная смазка.
В курсовом проекте в соответствии с полученными данными необходимо построить кинематическую схему механизмов иглы и нитепритягивателя. Кинематические схемы выполняют в масштабе, который рассчитывается по формуле:
Kl = ![]() (1)
(1)
L – действительные размеры кинематического звена, м;
l – размер этого звена на кинематической схеме, мм.
Kl = 0,014/56=1/4000=0,00025(м/мм)
|
Частота вращения главного вала, n, мин-1 |
Звено О1А, мм |
Звено О1С, мм |
Звено АС, мм |
Звено АВ, мм |
Звено О2D, мм |
Звено О2Х, мм |
Звено О2Y, мм |
Звено СD, мм |
Звено DE, мм |
Звено CE, мм |
| 5200 | 14 | 12 | 9 | 35 | 24 | 18 | 26 | 24 | 31 | 51 |
Таблица 1: исходные данные для построения кинематической схемы механизмов иглы и нитепритягивателя
Кинематическую схему механизма строят в следующем порядке. Вначале по заданным координатам x и y точек О1 и О2 (табл.1) в выбранном масштабе длин Кl, мм/мм, м/мм, (табл.2) наносят положение неподвижных точек О1 и О2 и проводят ось О1В неподвижной направляющей игловодителя, совпадающей с линией его движения. Затем из центра О1 радиусами
![]() О1 А =
О1 А =![]() и О1 С =
и О1 С =![]() мм проводят окружности - траектории
точек А и С.
мм проводят окружности - траектории
точек А и С.
Далее траектории этих точек разбивают на двенадцать равных частей (в точках (1,2,3,..,12 и 1',2',3'...,12'). Построение схемы механизмов в указанных 12 положениях выполняют с использованием метода засечек.
Кинематическая схема и разметка траекторий рабочих точек звеньев механизмов иглы и нитепритягивателя представлены в приложении.
Таблица 2: расчетные данные для построения кинематической схемы механизмов иглы и нитепритягивателя
|
Масштаб длин, Kl , м/мм |
Звено О1А, мм |
Звено О1С, мм |
Звено АС, мм |
Звено АВ, мм |
Звено О2D, мм |
Звено О2Х, мм |
Звено О2Y, мм |
Звено СD, мм |
Звено DE, мм |
Звено CE, мм |
| 0,00025 | 56 | 48 | 36 | 140 | 96 | 72 | 104 | 96 | 124 | 204 |
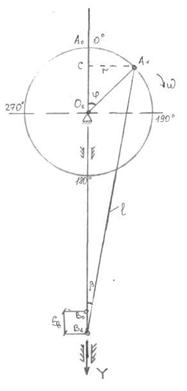
Основой для кинематического анализа является кинематическая схема рис.2
Перемещение точки В игловодителя определяется из рассмотрения различных положений кривошипно-шатунного механизма. Палец кривошипа, т.е. шарнир А1 из крайнего верхнего положения А0 проворачивается на угол φ. При этом игловодитель перемещается на величину Sв. Опустив из точки А перпендикуляр А1С на линию движения игловодителя О1В1 получим:
Sв = О1В1 – О1 В0 = (СВ1 - О1В1)-(А0В0 - А0О1) (2)
т.к. О1А1 = r , а А1В1 = l , тогда получим
Sв = (l.cosβ – r.cosφ) - (l - r) = r.(1 – cosφ) – l.(1 – cosβ) (3)
В полученное выражение φ и β – переменные величины
Рассмотрим ∆ СА1О1 и ∆ СА1В1 и выразим значение углов
СА1 = r.sinφ
СА1 = l.sinβ , тогда
sinβ = r/l. Sinφ (4)
|
|
Рисунок 2.
Разложим cosβ в степенной ряд, получим
cosβ = 1 - ![]() +
+
![]() +...... (5)
+...... (5)
влияние 3 и 4 ..... множителей не имеет значения, ими можно пренебречь, тогда получим выражение и подставим его в формулу (2), получим
Sв = r.(1 – cosφ) –![]() (6)
(6)
Дифференцируя это выражение по времени можно получить уравнение скорости и ускорения:
S’в = υВ = ![]() =
ω.r.(sinφ +
=
ω.r.(sinφ + ![]() )
(7)
)
(7)
S’’в =аВ = ![]() = ω2.r.( scosφ +
= ω2.r.( scosφ + ![]() )
(8)
)
(8)
График перемещения точки В
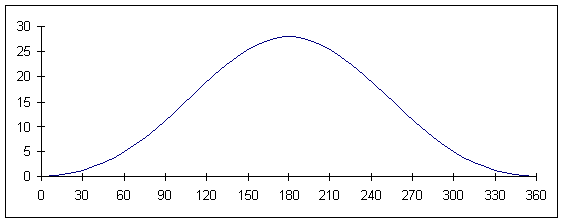
График скорости точки В
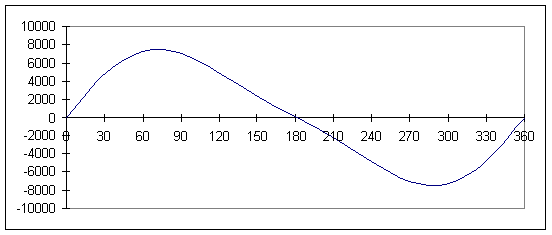
График ускорения точки В
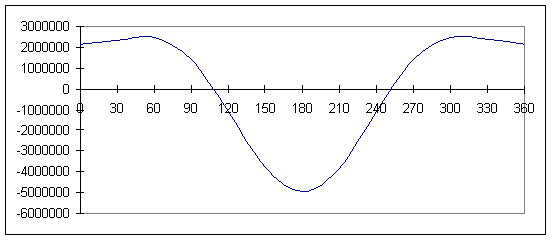
Рисунок 3
2 Определение скоростей звеньев механизмов иглы и нитепритягивателя
Если точка звена находится в движении относительно стойки и относительно подвижной точки другого типа, то определяются нормальные ускорения для обоих движений, а касательные ускорения находятся графически. При этом вектор нормального ускорения точки при движении ее относительно стойки откладывается из полюса плана, а при движении относительно подвижной точки — из конца ускорения этой точки.
При определении скоростей и ускорений задается закон движения ведущего звена. Закон движения задается частотой и направлением вращения ведущего звена. Так как ведущим звеном является кривошип 1, его частота вращения постоянна, т.е. он вращается равномерно, а, следовательно, ωО1А=const. Направление движения ведущего звена - по часовой стрелке.
Скорости точек А (механизма иглы) и С (механизма нитепритягивателя) рассчитываются по формулам:
![]() (9)
(9)
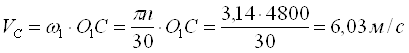 (10)
(10)
Векторы скоростей ![]() и
и
![]() направлены перпендикулярно
радиусам О1А и O1C в сторону вращения этих звеньев
(Кv, м/(с.мм) масштаб плана скоростей, который выбирается произвольно с учетом размеров чертежа).
направлены перпендикулярно
радиусам О1А и O1C в сторону вращения этих звеньев
(Кv, м/(с.мм) масштаб плана скоростей, который выбирается произвольно с учетом размеров чертежа).
![]() (11)
(11)
![]() (12)
(12)
План скоростей начинают строить с выбора произвольной точки на чертеже, которая называется полюсом скоростей (PV). Скорости откладывают в соответствии с масштабом скоростей:
Скорость точки D на плане скоростей определяется путем совместного решения двух векторных уравнений, (она принадлежит звеньям 4 и 5) сложением векторов:
 (13)
(13)
![]() При определении скорости
движения точки D за полюсы вращения принимаются точки С и О2
. В соответствии с правилами сложения
векторов из конца первого вектора Vc провопят линию действия скорости
При определении скорости
движения точки D за полюсы вращения принимаются точки С и О2
. В соответствии с правилами сложения
векторов из конца первого вектора Vc провопят линию действия скорости ![]() .
Затем из полюса Pv проводят линию действия скорости
.
Затем из полюса Pv проводят линию действия скорости ![]() (
(![]() так как первый
вектор
так как первый
вектор ![]() = 0). Пересечение линий
действия скоростей
= 0). Пересечение линий
действия скоростей ![]() и
и ![]() определяет положение точки
d на плане скоростей. Далее
все векторы скоростей направляют к найденной точке d и получают длины
векторов скоростей
определяет положение точки
d на плане скоростей. Далее
все векторы скоростей направляют к найденной точке d и получают длины
векторов скоростей ![]() и
и ![]() в выбранном масштабе плана скоростей КV.
в выбранном масштабе плана скоростей КV.
Скорость движения точки Е, (глазка нитепритягивателя) определяют по двум векторным уравнениям:
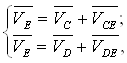 (14)
(14)
где ![]() и
и
![]()
Соединив полюс PV с точкой е, получают вектор скорости точки Е, т.е.
VE = VO . e результате построения треугольник cde должен быть подобен треугольнику CDE. Все стороны их должны быть взаимно перпендикулярны и сходственно расположены.
На основании подобия треугольников cde и CDE положение точки е на плане скоростей можно определить путем построения от линии cd треугольника cde подобного треугольнику CDE, не решая двух уравнений.
Положение точки е на плане скоростей можно найти также методом засечек.
Скорость движения точки В игловодителя определяют путем решения двух векторных уравнений:
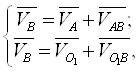 (15)
(15)
В соответствии с правилами сложения векторов
из конца первого вектора ![]() проводят линию действия скорости
проводят линию действия скорости ![]() . Далее из полюса
. Далее из полюса ![]() проводят
линию действия скорости
проводят
линию действия скорости ![]() в
направлении перемещения игловодителя (вертикально), так как первый вектор
в
направлении перемещения игловодителя (вертикально), так как первый вектор ![]() . Пересечение линий
действия скоростей
. Пересечение линий
действия скоростей ![]() и
и ![]() определить положение точки
в на плане скоростей.
определить положение точки
в на плане скоростей.
3 Определение ускорений звеньев механизмов иглы и нитепритягивателя и построение плана ускорений
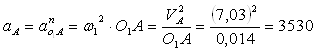 (16)
(16)
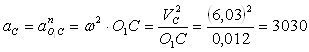 (17)
(17)
При ω=const касательная составляющая ускорений ![]() =
0,
=
0, ![]() = 0.
= 0.
Для построения плана ускорений выбирается масштаб ускорений Ka, м/(с2*мм), который рассчитывается как:
Ka = ![]() (18)
(18)
Из произвольно выбранной точки - полюса плана ускорений откладывают
(Ра) - откладывают вектор ac = ![]() направленный по
линии CO1 к полюсу вращения О1 . В результате на плане ускорений получают
точку с, к которой направлен вектор aoC = ac .
направленный по
линии CO1 к полюсу вращения О1 . В результате на плане ускорений получают
точку с, к которой направлен вектор aoC = ac .
Линейное ускорение точки D определяют путем решения следующих векторных уравнений:
 ,
(19)
,
(19)
![]() где a02 = 0 (точка О2
неподвижна).
где a02 = 0 (точка О2
неподвижна).
Величины нормальных составляющих ускорений, входящих в систему уравнений (19) определяют по формулам:
![]() =
= ![]() =
=
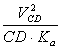 =
= 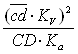 ;
(20)
;
(20)
![]() =
= ![]() (21)
(21)
![]()
![]()
![]()
Векторы касательных составляющих ускорений, входящих в систему уравнений (10) на плане ускорений направляют следующим образом:
![]()
В соответствии с
уравнением (10) из конца вектора ![]() , т.е.
точки с, на плане ускорений проводят вектор
, т.е.
точки с, на плане ускорений проводят вектор ![]() параллельно
линии CD в направлении от точки D к полюсу вращения – точке С (вниз).
Далее из конца вектора
параллельно
линии CD в направлении от точки D к полюсу вращения – точке С (вниз).
Далее из конца вектора ![]() проводят
перпендикуляр – линию действия
проводят
перпендикуляр – линию действия ![]() .
.
Во втором векторном
уравнении (10) вектор ![]() , поэтому из
полюса ускорений
, поэтому из
полюса ускорений ![]() проводят вектор
проводят вектор ![]() параллельно линии
параллельно линии ![]() в направлении от точки
в направлении от точки ![]() к точке
к точке ![]() (влево). Из конца этого
вектора проводят перпендикуляр к нему – линию действия
(влево). Из конца этого
вектора проводят перпендикуляр к нему – линию действия ![]() . Пересечение линий
действий касательных ускорений определяет положение точки d на плане ускорений.
. Пересечение линий
действий касательных ускорений определяет положение точки d на плане ускорений.
Соединив полюс плана
ускорений точку ![]() с точкой d, получают вектор ускорения
с точкой d, получают вектор ускорения ![]() . При этом все ранее
построенные векторы направлены к точке d.
. При этом все ранее
построенные векторы направлены к точке d.
Теорема подобия справедлива и для плана ускорений. Поэтому значительно проще найти положение точки е на плане ускорений, построив от линии cd треугольник cde, подобный треугольнику CDE на схеме механизма и сходственно с ним расположенный.
Для нанесения на план
ускорений точки е можно использовать метод засечек так же, как и при построении
плана скоростей. Для этого соответственно из точек d и c в
нужном направлении делают засечки дуг радиусами, равными длине векторов ![]() и
и ![]() , мм:
, мм:
![]() (22)
(22)
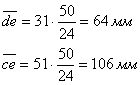
На следующем этапе
кинематического анализа из полюса плана ускорений ![]() откладывают
вектор
откладывают
вектор ![]() направленный по линии ОА1
к полюсу вращения О1. В результате на плане ускорений получают точку
а, к которой направлен вектор
направленный по линии ОА1
к полюсу вращения О1. В результате на плане ускорений получают точку
а, к которой направлен вектор ![]() .
.
Линейное ускорение точки В определяют путем решения следующих векторных уравнений:
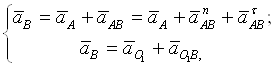 (23)
(23)
где ![]() =0 (точка О1
неподвижна).
=0 (точка О1
неподвижна).
Вектор нормальный
составляющей ускорения ![]() , входящей в
систему уравнений (23) определяют по формулам:
, входящей в
систему уравнений (23) определяют по формулам:
 .
(24)
.
(24)
![]()
Вектор касательной
составляющей ускорения ![]() , входящих в
систему уравнений (23) на плане ускорений направляют следующим образом:
, входящих в
систему уравнений (23) на плане ускорений направляют следующим образом: ![]() .
.
В соответствии с
уравнениями (14) из конца вектора ![]() , т.е.
точки а, на плане ускорений проводят вектор
, т.е.
точки а, на плане ускорений проводят вектор ![]() параллельно
линии АВ в направлении к полюсу вращения – точке
параллельно
линии АВ в направлении к полюсу вращения – точке ![]() .
Далее из конца вектора
.
Далее из конца вектора ![]() проводят
перпендикуляр – линию действия
проводят
перпендикуляр – линию действия ![]() .
.
Во втором векторном
уравнении (14) вектор ![]() , поэтому из
полюса ускорений
, поэтому из
полюса ускорений ![]() проводят вектор
проводят вектор ![]() параллельно линии
параллельно линии ![]() в направлении к точке
в направлении к точке ![]() . Пересечение линий
действий касательного ускорения
. Пересечение линий
действий касательного ускорения ![]() и
ускорения
и
ускорения ![]() определяет положение точки
в на плане ускорений.
определяет положение точки
в на плане ускорений.
Для нанесения на план
ускорений точек центров тяжести, можно воспользоваться теоремой подобия.
Например, для точки ![]() - центра тяжести
звена 5 – можно составить пропорцию:
- центра тяжести
звена 5 – можно составить пропорцию:
![]() (25)
(25)
и полученный отрезок
отложить из полюса ![]() по направлению к
точке
по направлению к
точке ![]() .
.
План ускорений позволяет
определить линейное ускорение любой точки на всяком звене, ![]() , используя следующие
формулы:
, используя следующие
формулы:
 (26)
(26)
Построив план линейных
ускорений, можно определить угловые ускорения, ![]() ,
звеньев механизма:
,
звеньев механизма:
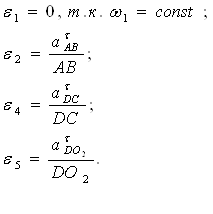 (27)
(27)
Таблица 3: данные для построения ускорений механизмов иглы и нитепритягивателя
|
|
|
|
|
|
|
| 11 | 0,54 | 3,4 | 64 | 106 | 0,028 |
| 1 | 2,9 | 1,9 | 43 | 70 | 0,058 |
| 2 | 45,4 | 2 | 64 | 106 | 0,008 |
4 Силовой анализ механизма
Силовой анализ выполняется с целью определения усилий между звеньями в кинематических парах и уравнивающей силы и момента на главном валу. Эти задачи имеют большое практическое значение. На основании первой задачи решается вопрос о коэффициенте полезного действия машины, вторая задача позволяет определить необходимую мощность двигателя для приведения в действие машины.
Силовой анализ необходим для расчета прочности звеньев, кинематических пар и станин механизмов или машин при их проектировании.
Силовой анализ проводят в порядке, обратном кинематическому анализу, т.е. начинают с наиболее удаленных от ведущего звена структурных групп и заканчивают структурной группой первого класса, состоящей из стойки и ведущего звена, т.е. кривошипа.
Началом силового анализа
является определение сил, действующих на звенья механизмов. Такими силами
являются силы тяжести звеньев ![]() , силы
полезного сопротивления
, силы
полезного сопротивления ![]() , силы
инерции
, силы
инерции ![]() и другие внешние силы.
и другие внешние силы.
Силы тяжести обычно определяются взвешиванием звеньев. Эти силы прикладываются в центрах тяжести звеньев. Силы полезного сопротивления зависят от выполняемого технологического процесса. Они устанавливаются экспериментально и прикладываются в рабочих точках механизма.
Силы инерции рассчитываются по формуле
![]() ,
(28)
,
(28)
где m – масса звена, г;
![]() - ускорение центра тяжести
звена,
- ускорение центра тяжести
звена, ![]() .
.
![]()
Силы инерции приложены в центре тяжести звена и направлены в сторону, противоположную его ускорению.
Если звено находится в сложном (плоскопараллельном) движении, то одновременно возникает сила инерции, направленная против ускорения центра тяжести, и момент пары сил инерции, направленный против углового ускорения звена.
Эта сила и момент заменяются одной результирующей силой инерции, равной произведению массы звена на ускорение его центра тяжести и приложенной в некоторой точке k.
Положение точки k, к которой приложена результирующая сила инерции, определяет плечо h, величина которого вычисляется по формуле
![]() , (29)
, (29)
где Мu – момент сил инерции
Is – момент инерции звена относительно оси, проходящей через центр тяжести звена; для стержня постоянного сечения;
![]() (30)
(30)
![]() - длина звена, м;
- длина звена, м;
![]() - угловое ускорение звена,
- угловое ускорение звена, ![]() ;
;
m – масса звена, кг;
![]() - ускорение центра тяжести звена,
- ускорение центра тяжести звена, ![]() .
.
![]()
Подставим числа в (30) формулу:
![]()
![]()
Подставим все в (29) формулу:
![]()
Для выполнения силового
анализа строят схему механизма в определенном масштабе длин ![]() , мм/мм, м/мм, и
прикладывают в соответствующих точках звеньев действующие силы. После этого
приступают к определению реакций в кинематических парах. Для швейных машин
силовой анализ, как правило, выполняют без учета сил трения. Их учитывают при
определении момента движущих сил, вводя коэффициент, равный 1,2-1,4.
, мм/мм, м/мм, и
прикладывают в соответствующих точках звеньев действующие силы. После этого
приступают к определению реакций в кинематических парах. Для швейных машин
силовой анализ, как правило, выполняют без учета сил трения. Их учитывают при
определении момента движущих сил, вводя коэффициент, равный 1,2-1,4.
Наиболее просто силовой
анализ можно выполнить графическим способом – путем построения планов сил в
некотором масштабе ![]() , Н/мм. Поскольку
при силовом анализе в расчет вводят силы инерции и реакции связей, то все силы,
действующие на структурные группы 2 класса 2 порядка, находятся в равновесии.
Поэтому векторное уравнение этих сил, равняется нулю, а многоугольник сил
замкнут. Необходимо помнить, что кинематические цепи, имеющие степень
подвижности w=0, в силовом отношении являются
статически определенными. Условие статической определимости плоских
кинематических цепей записывается в виде:
, Н/мм. Поскольку
при силовом анализе в расчет вводят силы инерции и реакции связей, то все силы,
действующие на структурные группы 2 класса 2 порядка, находятся в равновесии.
Поэтому векторное уравнение этих сил, равняется нулю, а многоугольник сил
замкнут. Необходимо помнить, что кинематические цепи, имеющие степень
подвижности w=0, в силовом отношении являются
статически определенными. Условие статической определимости плоских
кинематических цепей записывается в виде:
![]() ,
(31)
,
(31)
где n - число подвижных звеньев;
![]() - число кинематических пар 5 и 4
классов;
- число кинематических пар 5 и 4
классов;
3 – число уравнений статики, которое можно составить для каждого подвижного звена в плоскости.
В общем случае реакция в поступательной кинематической паре 5 класса известна лишь по направлению (перпендикулярно к направляющей), величина и точка ее положения неизвестны. Во вращательной кинематической паре 5 класса известна точка приложения реакции (в центре шарнира), величина же и направление ее неизвестны. В кинематической паре 4 класса известны точка приложения (в точке касания) и направление (перпендикулярно касательной к профилям кривых) реакции. Неизвестна лишь ее величина.
Для уравновешивания
кинематической цепи 1 класса вводят уравновешивающий момент ![]() или уравновешивающую силу
или уравновешивающую силу ![]() . Связь между
. Связь между ![]() и
и ![]() устанавливается
уравнением:
устанавливается
уравнением:
![]() ,
(32)
,
(32)
где ![]() - плечо силы
- плечо силы ![]() относительно оси вращения
кривошипа.
относительно оси вращения
кривошипа.
При силовом анализе при вращательном движении кривошипа вводят уравновешивающий момент.
Применительно к механизму иглы универсальной швейной машины 1022 класса силовой анализ выполняется в следующей последовательности.
Силовой анализ начинают
со структурной группы наиболее удаленной от ведущего звена, т.е. со звена II класса, 2 порядка А-2-![]() -3-В. Эту цепь мысленно
отсоединяют от ведущего звена 1 и стойки 0, при этом вводятся реакции
-3-В. Эту цепь мысленно
отсоединяют от ведущего звена 1 и стойки 0, при этом вводятся реакции ![]() и
и ![]() . Индексы на обозначениях
реакций и кинематических пар принято ставить со стороны отсоединенного звена на
рассматриваемое. Реакция
. Индексы на обозначениях
реакций и кинематических пар принято ставить со стороны отсоединенного звена на
рассматриваемое. Реакция ![]() неизвестна
по величине и направлению, реакция
неизвестна
по величине и направлению, реакция ![]() приложена
в точке В и линия ее действия перпендикулярна направляющей ползуна.
приложена
в точке В и линия ее действия перпендикулярна направляющей ползуна.
Реакцию ![]() раскладывают на две
составляющие: по звену АВ и перпендикулярно этому звену, т.е.
раскладывают на две
составляющие: по звену АВ и перпендикулярно этому звену, т.е.
![]() .
(33)
.
(33)
Векторное уравнение сил, действующих на рассматриваемую кинематическую цепь имеет вид:
![]() . (34)
. (34)
Сила полезного
сопротивления ![]() действует не во
всех положениях механизма, а лишь при рабочем ходе иглы.
действует не во
всех положениях механизма, а лишь при рабочем ходе иглы.
Как видно из уравнения
(34) силы ![]() известны полностью по
величине, направлению и точке положения. В случае, когда силы тяжести малы по
сравнению с другими силами, их можно не учитывать.
известны полностью по
величине, направлению и точке положения. В случае, когда силы тяжести малы по
сравнению с другими силами, их можно не учитывать.
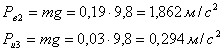
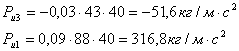
В уравнении (34) не вошли
реакции ![]() , действующие между
звеньями 2 и 3, приложенные в точке В. Эти реакции взаимно уравновешиваются
внутри структурной группы. Они относятся к разряду внутренних сил. Эти силы
определяются на последующих этапах силового анализа.
, действующие между
звеньями 2 и 3, приложенные в точке В. Эти реакции взаимно уравновешиваются
внутри структурной группы. Они относятся к разряду внутренних сил. Эти силы
определяются на последующих этапах силового анализа.
В уравнении (34) имеются три неизвестные силы, и для их определения рассматривается равновесие звена 2. Для этого звена векторное уравнение сил имеет следующий вид:
![]() (35)
(35)
Для определения ![]() необходимо составить
уравнение моментов сил относительно точки В:
необходимо составить
уравнение моментов сил относительно точки В:
![]() (36)
(36)
Моменты сил ![]() и
и ![]() равны нулю, так как их
плечи равны нулю. Тогда:
равны нулю, так как их
плечи равны нулю. Тогда:
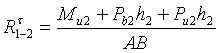 (37)
(37)
![]()
Для получения
составляющей реакции ![]() с минусом
следует повернуть ее на
с минусом
следует повернуть ее на ![]() .
.
Далее приступают к
построению плана сил. Выбирают произвольную точку ![]() и
откладывают от нее в соответствии с уравнением (34) поочередно в масштабе
векторы известных сил.
и
откладывают от нее в соответствии с уравнением (34) поочередно в масштабе
векторы известных сил.
Модули (величины)
векторов сил зависят от выбранного масштаба сил ![]() ,
Н/мм, т.е.
,
Н/мм, т.е.
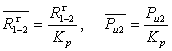 (38)
(38)
Из конца последнего
вектора силы ![]() проводят линию действия
силы
проводят линию действия
силы ![]() перпендикулярно
направляющей игловодителя (горизонтально), а из начальной точки
перпендикулярно
направляющей игловодителя (горизонтально), а из начальной точки ![]() проводят линию действия
проводят линию действия ![]() параллельно АВ. Точка
параллельно АВ. Точка ![]() пересечения последних двух
линий будет концом вектора силы
пересечения последних двух
линий будет концом вектора силы ![]() и
началом составляющей реакции
и
началом составляющей реакции![]() . В
соответствии с уравнением (34) заменяют составляющие
. В
соответствии с уравнением (34) заменяют составляющие ![]() и
и ![]() на полную величину реакции
на полную величину реакции
![]() . Из плана сил получают:
. Из плана сил получают:
![]()
Затем определяют реакцию ![]() , приложенную в шарнире
, приложенную в шарнире ![]() . Для этого используют
имеющийся уже план сил и уравнение (36). Очевидно, реакция
. Для этого используют
имеющийся уже план сил и уравнение (36). Очевидно, реакция ![]() будет направлена по прямой
линии, замыкающей начало
будет направлена по прямой
линии, замыкающей начало ![]() и конец
и конец
![]() . Тогда
. Тогда
![]()
На следующем этапе
силового анализа рассматривают структурную группу 1 класса ![]() . Векторное уравнение сил
записывают в следующем виде:
. Векторное уравнение сил
записывают в следующем виде:
![]() (39)
(39)
где ![]() , равная
, равная ![]() .
.
Для определения ![]() сразу строят план сил в
том же масштабе
сразу строят план сил в
том же масштабе ![]() . Начиная от
точки
. Начиная от
точки ![]() проводят векторы
проводят векторы ![]() ,
, ![]() ,
, ![]() . Конец последнего вектора
соединяют с точкой
. Конец последнего вектора
соединяют с точкой ![]() - началом
вектора
- началом
вектора ![]() . Значение реакции
. Значение реакции ![]() составляет:
составляет:
![]()
Величину
уравновешивающего момента ![]() определяют,
составив уравнение моментов сил, действующих на первое звено относительно точки
определяют,
составив уравнение моментов сил, действующих на первое звено относительно точки
![]() , т.е.
, т.е.
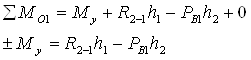 (40)
(40)
Знаки «+» и «-» показывают
истинное направление ![]() .
.
Планы сил строят для нескольких положений механизма, из которых находят наибольшее значение сил и реакций. Эти значения сил используют в расчетах на прочность деталей механизмов и кинематических пар машины.
Таблица 4: данные для силового анализа механизма и для построения плана сил
|
|
|
|
|
|
|
h | |
| 11 | 86 | 41 | -51,6 | 316,8 | -6536 | -186663,9 | 0,0014 |
| 1 | 60 | 50 | -68,4 | 316,8 | -456 | -12943,9 | 0,0024 |
| 2 | 61 | 88 | -103,2 | 316,8 | -463 | -13119,9 | 0,0042 |
ЗАКЛЮЧЕНИЕ
Выполняя курсовой проект, я обобщила, углубила и закрепила знания, полученных мною на лекциях и при выполнении лабораторных работ по дисциплине «Оборудование для швейного производства и основы проектирования оборудования», и их применение при решении технических, технологических, научных и экономических задач, возникающих при проектировании швейного оборудования.
Также в процессе работы я ознакомилась с основными этапами проектирования швейного оборудования, изучила технологический процесс, осуществляемый на универсальной швейной машине, научилась составлять и анализировать кинематические схемы исполнительных механизмов. Еще я освоила методику проведения перемещений, скоростей, ускорений звеньев механизмов и их отдельных точек, научилась устанавливать законы изменения во времени этих величин, определять силы, действующие на звенья механизмов, реакции в кинематических парах и давления на станину машины. Таким образом, я научилась решать задачи кинематического и динамического анализа механизмов, необходимого для выполнения расчетов проектируемого швейного оборудования.
При выполнении курсового проекта я учитывала основные задачи, стоящие перед швейной промышленностью по техническому перевооружению производства, применению современных средств механизации и автоматизации оборудования, созданию конкурентоспособного оборудования, экономному использованию материальных и трудовых ресурсов.
СПИСОК ИСПОЛЬЗУЕМОЙ ЛИТЕРАТУРЫ
1. Теория механизмов и механика машин [Текст]: учеб. для втузов/К. В. Фролов [и др.]; Изд. 4-е, испр.; М.: Высш. шк., 2003. 496 с.: ил.
2. Иосилевич Г. Б. Прикладная механика [Текст]: учеб. для вузов/ Под ред. Г. Б. Иосилевича; М.: Высш. шк., 1989. 351 с.: ил.
3. Оборудование швейного производства [Текст]: учеб. для вузов/ Вальщиков Н. М.; М.: Легкая индустрия, 1977, 520 с.: ил.
4. Вальщиков Н. М. Расчет и проектирование машин швейного производства [Текст]: учеб. для вузов/ Н. М. Вальщиков; Л.; Машиностроение, 1973, 343 с.
5. Гарбарук В. П. Расчет и конструирование основных механизмов челночных швейных машин [Текст]: учеб. для вузов/ В. П. Гарбарук; Л.; Машиностроение, 1977, 231 с.
6. Лабораторный практикум по машинам и аппаратам швейного производства [Текст]: учеб. пособие/ Б. А. Рубцов; М.: Легпромбытиздат, 1995, 256 с.
Рисунок 1.1 Пространственная кинематическая схема механизмов иглы и нитепритягивателя машины 1022 кл.
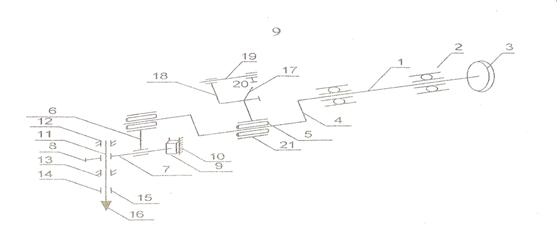
1 – главный вал
2 – втулки направляющие – подшипники скольжения
3 – шкив (маховик)
4 – кривошип игловодителя с противовесом
5 – палец кривошипа
6 – шатун
7 – поводок (шарнирная шпилька)
8 – стягивающий винт
9 – ползун
10 – направляющий паз
11 – игловодитель
12, 13 – втулки игловодителя (верхняя и нижняя)
14 – иглодержатель
15 – упорный винт для крепления иглы
16 – игла
17 – рычаг нитепритягивателя, надетый на внутреннее плечо пальца 5
18 – соединительное звено
19 – шарнирный палец
20 – установочный винт для закрепления пальца в корпусе машины
21 – игольчатый подшипник
| Ответы к экзаменационным билетам по физике 11 класс (ответы к 29 ... | |
|
Билет №1 Механическое движение - это изменение положения тела в пространстве с течением времени относительно других тел. Из всех многообразных форм ... Предположим, что тело движется без ускорения (самолет на маршруте), его скорость в течение продолжительного времени не меняется, а = 0, тогда кинематические уравнения будут иметь ... Вектор ускорения при движении по окружности направлен перпендикулярно вектору скорости (направленному по касательной), к центру окружности. |
Раздел: Рефераты по физике Тип: реферат |
| Кинематический анализ механизма транспортирования ткани | |
|
Кинематический анализ механизма верхней и нижней реек швейной машины 131-42+3 класса. Реферат Отчет с., 1 ч., 46 рис., 3 табл., 88 источников, 1 прил ... Наиболее широкое применение нашел метод замкнутых векторных контуров, предложенный В.А.Зиновьевым [2]. Метод основан на представлении кинематической цепи в виде нескольких ... В результате кинематического анализа механизма транспортирования ткани швейной машины на ЭВМ определяется ряд дискретных значений координат XQi и YQi, (i - номер положения входного ... |
Раздел: Рефераты по технологии Тип: реферат |
| Проектирование и исследование механизмов двухцилиндрового ДВС | |
|
Кафедра "Теории механизмов и машин" РАСЧЕТНО-ПОЯСНИТЕЛЬНАЯ ЗАПИСКА К КУРСОВОЙ РАБОТЕ НА ТЕМУ: "Проектирование и исследование механизмов 2-х ... Из полюса р проводим прямую, параллельную AC до пересечения с прямой, проведенной из точки b. Обозначим точку пересечения через c. Расставим стрелки векторов в соответствии с ... У каждого шатуна известны скорости точек B и D. Принимая точки B и D за полюсы, запишем векторные уравнения для определения ускорения точек Е и С: |
Раздел: Промышленность, производство Тип: курсовая работа |
| Разработка алгоритмов контроля и диагностики системы управления ... | |
|
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ "ХАРКІВСЬКИЙ ПОЛІТЕХНІЧНИЙ ІНСТИТУТ" Факультет І Кафедра "Системи та процеси ... Наряду с динамическими уравнениями рассматриваются кинематические уравнения, связывающие угловые скорости j с углами поворота триэдра осей Oxyz относительно триэдра осей некоторой ... Оси инерции (или оси формы) космического аппарата не совпадают с инерциальным базисом, а вращаются относительно него в зависимости от направления вектора скорости центра масс ... |
Раздел: Рефераты по авиации и космонавтике Тип: реферат |
| Электрические аппараты | |
|
Раздел 1. Основы теории электрических аппаратов Лекция № 1 Электрический аппарат - это электротехническое устройство, которое используется для ... Поскольку формула Максвелла учитывает реальную индукцию между полюсами, то она также может быть использована при условии, что поле в зазоре равномерно и вектор индукции ... Если изобразить соответствующими векторами, то амплитуда переменной составляющей может быть найдена из векторной диаграммы |
Раздел: Рефераты по физике Тип: учебное пособие |