Курсовая работа: Методика составления психологического опросника
ОГЛАВЛЕНИЕ:
Введение
1. Составление опросника
2. Анализ трудности задания
3. Вычисление индекса дискриминативности
3.1. Вычисление коэффициента дискриминации
3.2. Вычисление индекса дискриминации
4. Определение надёжности теста
4.1. Определение надёжности целого теста
4.2. Определение надежности частей теста
5. Определение валидности теста
6. Стандартизация показателей (z-преобразование оценок)
7. Определение асимметрии и эксцесса распределения
Заключение
Список использованной литературы
Приложение 1
Приложение 2
Приложение 3
Приложение 4
Приложение 5
ВВЕДЕНИЕ
В той или иной степени волнение и тревога знакомы каждому человеку. Даже маленькие дети испытывают чувство тревоги, хотя и не всегда осознанно. Бывают случаи, когда тревога выполняет положительную функцию - заставляет сконцентрироваться, тщательно подготовиться к предстоящему испытанию (например, к экзамену), повышает чувство ответственности. Но чаще бывает по-другому, страх приобретает совсем иную природу и вместо концентрации и мобилизации ресурсов приводит к их блокированию, начинает тормозить любые формы социальной активности и доставляет человеку (и лицам из его близкого окружения) массу неприятных переживаний. На фоне подобных переживаний могут возникать болезненные страхи, которые выражаются в навязчивых, странных и не понятных окружающим действиях, например, постоянном мытье рук из-за боязни заразиться или в навязчивом контроле за выросшими уже детьми из-за опасения, что с ними может произойти что-либо страшное.
ЦЕЛЬ ИССЛЕДОВАНИЯ: разработать тест-опросник для определения уровня страха перед будущим у студентов последних курсов гуманитарного колледжа. Мы надеемся, что разработанный нами опросник будет соответствовать установленным требованиям к опросникам и измерять подверженность страхам с достаточной валидностью и надежностью.
ОБЪЕКТ ИССЛЕДОВАНИЯ: тревога как психическое явление.
ПРЕДМЕТ ИССЛЕДОВАНИЯ: разработка теста-опросника, отражающего уровни тревоги и страха перед будущим у студентов.
ЗАДАЧИ ИССЛЕДОВАНИЯ:
1. рассмотреть понятие (структуру понятия);
2. разработать опросник;
3. провести анализ трудности задания;
4. рассчитать дискриминативность;
5. определить надёжность (ретестовую и надёж.частей теста);
6. вычислить валидность теста;
7. провести стандартизацию показателей;
8. рассчитать ассиметрию и эксцесс эмптрического исследования;
МЕТОДОЛОГИЯ: в данной курсовой работе использованы психологические методы: личностная шкала проявления тревоги Дж. Тейлор (адаптация Т. А. Немчинова) (Приложение 1), шкала лживости В. Г. Норакидзе. Также были использованы математические методы: программа «Excel». Проблеме тревожности посвящено большое число теоретических и эмпирических исследований, как в зарубежной, так и отечественной психологии. В своей работе мы опирались на труды Немова Р. С., Бурлачука Л.Ф., Морозова С.М.
ЭМПИРИЧЕСКАЯ БАЗА ИССЛЕДОВАНИЯ: Выборка, на которой проводилось исследование, представлена студентами последнего курса гуманитарного колледжа. Общее количество обследуемых - 50 человек, из них 26 девушек и 24 юноши, в возрасте от 17 - 21 года со средним возрастом 18,6 лет. Исследование проводилось 2 раза с интервалом в 1 месяц.
1. СОСТАВЛЕНИЕ ОПРОСНИКА
Целью разработки опросника является создание теста, определяющего уровень тревожности у студентов последних курсов. Наш опросник (Приложение 3) был разработан на базе опросника Дж.Тейлора, который отражает личностную шкалу проявления тревоги.
Разработанный нами опросник отражает уровень тревоги перед будущим у студентов последних курсов, направлен на диагностику страха. Тест состоит из 50 вопросов.
С помощью разработанного нами опроса на базе НОУ «Гуманитарный колледж» было протестировано 50 чел, из них 26 девушек и 24 юноши, в возрасте от 17 - 21 года со средним возрастом 18,6 лет. Исследование проводилось 2 раза с интервалом в 1 месяц. Первое исследование пилотажное и повторное - через месяц.
Структура опросника представлена в Таблице 1.
Таблица 1.
СТРУКТУРА ТРЕВОЖНОСТИ
| Шкала страха | Шкала лжи | |
| поведенческий | 5,11,14,18,30,31,32,34,41 | 8,12,36,45,47,49 |
| когнитивный |
2,3,9,15,19,21,22,24, 26,27,28,33,43,44,46,50 |
1,16,25 |
| эмоциональный |
4,6,7,10,13,17,20,29, 35,37,38,39,40,42,48 |
23 |
2. АНАЛИЗ ТРУДНОСТИ ЗАДАНИЯ (ITEM-АНАЛИЗ)
Анализ заданий по результатам, получившимся в пилотажном исследовании, имеет своей целью отбор окончательных вопросов опросника и включает в себя определение трудностей (сложностей) и дикриминативности каждого задания.
Для вычисления трудности задания используется следующая формула:
Uт=100![]() (1-
(1-![]() ) , где
) , где
Uт- индивидуальная трудность в процентах,
Nn-число испытуемых, правильно решивших данную задачу в соответствии с ключом (Приложение 4),
N- общее число испытуемых, N=50.
Вычисление трудности задания приведено таблице 2.
Таблица 2
|
Номер задания |
Nn |
Uт |
| 1 | 41 | 18 |
| 2 | 16 | 68 |
| 3 | 23 | 54 |
| 4 | 32 | 36 |
| 5 | 37 | 26 |
| 6 | 46 | 8 |
| 7 | 35 | 30 |
| 8 | 45 | 10 |
| 9 | 38 | 24 |
| 10 | 14 | 72 |
| 11 | 27 | 46 |
| 12 | 13 | 74 |
| 13 | 29 | 42 |
| 14 | 42 | 16 |
| 15 | 33 | 34 |
| 16 | 23 | 54 |
| 17 | 39 | 22 |
| 18 | 9 | 82 |
| 19 | 36 | 28 |
| 20 | 25 | 50 |
| 21 | 34 | 32 |
| 22 | 34 | 32 |
| 23 | 27 | 46 |
| 24 | 35 | 30 |
| 25 | 25 | 50 |
| 26 | 47 | 6 |
| 27 | 36 | 28 |
| 28 | 40 | 20 |
| 29 | 32 | 36 |
| 30 | 26 | 48 |
| 31 | 34 | 32 |
| 32 | 42 | 16 |
| 33 | 37 | 26 |
| 34 | 26 | 48 |
| 35 | 42 | 16 |
| 36 | 24 | 52 |
| 37 | 13 | 74 |
| 38 | 11 | 78 |
| 39 | 26 | 48 |
| 40 | 40 | 20 |
| 41 | 30 | 40 |
| 42 | 33 | 34 |
| 43 | 21 | 58 |
| 44 | 34 | 32 |
| 45 | 33 | 34 |
| 46 | 33 | 34 |
| 47 | 35 | 30 |
| 48 | 31 | 38 |
| 49 | 24 | 52 |
| 50 | 33 | 34 |
Учитывая, что допустимые пределы трудности задания составляют от 16 до 84%, то задания под номерами 6,8, 26 удаляются из опросника, так как они не соответствуют этой трудности.
3. ВЫЧИСЛЕНИЕ ИНДЕКСА ДИСКРИМИНАТИВНОСТИ
Дискриминативность – это способность отделять испытуемых с высоким общим баллом по тесту от тех, кто получил низкий балл.
Для вычисления индекса дискриминативности необходимо вычислить стандартное отклонение оценок всех испытуемых выборки по формуле:
Sx=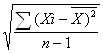 , где
, где
Sx-стандартное отклонение индивидуальных оценок всех испытуемых выборки,
Xi- индивидуальный балл каждого испытуемого по всему тесту,
![]() - среднее арифметическое оценок по
всему тесту всех испытуемых,
- среднее арифметическое оценок по
всему тесту всех испытуемых,
n-общее количество испытуемых, n=50;
Среднее арифметическое можно вычислить по формуле:
![]() =
=![]()
Индивидуальные баллы каждого испытуемого по всему тесту и их сумма приведены в таблице 3.
Таблица 3
|
i |
Xi |
| 1 | 46 |
| 2 | 43 |
| 3 | 40 |
| 4 | 30 |
| 5 | 35 |
| 6 | 17 |
| 7 | 27 |
| 8 | 22 |
| 9 | 18 |
| 10 | 38 |
| 11 | 42 |
| 12 | 39 |
| 13 | 32 |
| 14 | 45 |
| 15 | 39 |
| 16 | 44 |
| 17 | 15 |
| 18 | 47 |
| 19 | 36 |
| 20 | 35 |
| 21 | 28 |
| 22 | 16 |
| 23 | 26 |
| 24 | 38 |
| 25 | 42 |
| 26 | 30 |
| 27 | 13 |
| 28 | 43 |
| 29 | 36 |
| 30 | 21 |
| 31 | 40 |
| 32 | 48 |
| 33 | 36 |
| 34 | 18 |
| 35 | 40 |
| 36 | 43 |
| 37 | 17 |
| 38 | 27 |
| 39 | 15 |
| 40 | 19 |
| 41 | 29 |
| 42 | 26 |
| 43 | 34 |
| 44 | 32 |
| 45 | 19 |
| 46 | 16 |
| 47 | 25 |
| 48 | 17 |
| 49 | 18 |
| 50 | 39 |
|
∑Xi |
1541 |
На основании таблицы среднее арифметическое:
![]() =
=![]() =
=![]() =30,82;
=30,82;
Таблица 4
|
i |
Xi |
|
|
| 1 | 46 | 15,18 | 230,4324 |
| 2 | 43 | 12,18 | 148,3524 |
| 3 | 40 | 9,18 | 84,2724 |
| 4 | 30 | -0,82 | 0,6724 |
| 5 | 35 | 4,18 | 17,4724 |
| 6 | 17 | -13,82 | 190,9924 |
| 7 | 27 | -3,82 | 14,5924 |
| 8 | 22 | -8,82 | 77,7924 |
| 9 | 18 | -12,82 | 164,3524 |
| 10 | 38 | 7,18 | 51,5524 |
| 11 | 42 | 11,18 | 124,9924 |
| 12 | 39 | 8,18 | 66,9124 |
| 13 | 32 | 1,18 | 1,3924 |
| 14 | 45 | 14,18 | 201,0724 |
| 15 | 39 | 8,18 | 66,9124 |
| 16 | 44 | 13,18 | 173,7124 |
| 17 | 15 | -15,82 | 250,2724 |
| 18 | 47 | 16,18 | 261,7924 |
| 19 | 36 | 5,18 | 26,8324 |
| 20 | 35 | 4,18 | 17,4724 |
| 21 | 28 | -2,82 | 7,9524 |
| 22 | 16 | -14,82 | 219,6324 |
| 23 | 26 | -4,82 | 23,2324 |
| 24 | 38 | 7,18 | 51,5524 |
| 25 | 42 | 11,18 | 124,9924 |
| 26 | 30 | -0,82 | 0,6724 |
| 27 | 13 | -17,82 | 317,5524 |
| 28 | 43 | 12,18 | 148,3524 |
| 29 | 36 | 5,18 | 26,8324 |
| 30 | 21 | -9,82 | 96,4324 |
| 31 | 40 | 9,18 | 84,2724 |
| 32 | 48 | 17,18 | 295,1524 |
| 33 | 36 | 5,18 | 26,8324 |
| 34 | 18 | -12,82 | 164,3524 |
| 35 | 40 | 9,18 | 84,2724 |
| 36 | 43 | 12,18 | 148,3524 |
| 37 | 17 | -13,82 | 190,9924 |
| 38 | 27 | -3,82 | 14,5924 |
| 39 | 15 | -15,82 | 250,2724 |
| 40 | 19 | -11,82 | 139,7124 |
| 41 | 29 | -1,82 | 3,3124 |
| 42 | 26 | -4,82 | 23,2324 |
| 43 | 34 | 3,18 | 10,1124 |
| 44 | 32 | 1,18 | 1,3924 |
| 45 | 19 | -11,82 | 139,7124 |
| 46 | 16 | -14,82 | 219,6324 |
| 47 | 25 | -5,82 | 33,8724 |
| 48 | 17 | -13,82 | 190,9924 |
| 49 | 18 | -12,82 | 164,3524 |
| 50 | 39 | 8,18 | 66,9124 |
|
|
5441,38 |
На основании таблицы 4 стандартное отклонение оценок всех испытуемых выборки можно вычислить следующим образом:
Sx=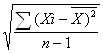 =
=![]() =10,538;
=10,538;
3.1 Вычисление коэффициента дискриминации
Исходя из того, что в нашем опроснике каждое задание будет оцениваться по двухбалльной шкале («верно», «не верно»), мы вычисляем коэффициент дискриминации по формуле:
r![]() =
=![]() , где
, где
r![]() -коэффициент дискриминации,
-коэффициент дискриминации,
![]() - среднее арифметическое оценок по тесту у испытуемых,
правильно выполнивших задание в соответствии с ключом,
- среднее арифметическое оценок по тесту у испытуемых,
правильно выполнивших задание в соответствии с ключом,
N+-число испытуемых, правильно решивших задачу (тех, чей ответ на данный пункт опросника соответствует ключу),
![]() - среднее арифметическое оценок по
всему тесту всех испытуемых,
- среднее арифметическое оценок по
всему тесту всех испытуемых, ![]() = 30,82;
= 30,82;
Sx - стандартное отклонение индивидуальных оценок всех испытуемых выборки,
Sx= 10,538;
N - общее количество испытуемых, N=50;
Вычисление коэффициента дискриминации сведено в таблицу 5.
Таблица 5
|
Номер задания |
|
|
r |
| 1 | 41 | 26,66 | -0,8 |
| 2 | 16 | 10,64 | -1,3 |
| 3 | 23 | 15,96 | -1,3 |
| 4 | 32 | 21,46 | -1,1 |
| 5 | 37 | 24,22 | -1,0 |
| 6 | 46 | 28,94 | -0,6 |
| 7 | 35 | 22,3 | -1,2 |
| 8 | 45 | 28,92 | -0,5 |
| 9 | 38 | 24,84 | -1,0 |
| 10 | 14 | 10,04 | -1,2 |
| 11 | 27 | 18,7 | -1,2 |
| 12 | 13 | 9,4 | -1,2 |
| 13 | 29 | 20,14 | -1,1 |
| 14 | 42 | 27,32 | -0,7 |
| 15 | 33 | 22,26 | -1,1 |
| 16 | 23 | 18,46 | -1,0 |
| 17 | 39 | 25,2 | -1,0 |
| 18 | 9 | 7,16 | -1,0 |
| 19 | 36 | 25,4 | -0,8 |
| 20 | 25 | 18,84 | -1,1 |
| 21 | 34 | 24,3 | -0,9 |
| 22 | 34 | 23,8 | -0,9 |
| 23 | 27 | 18,9 | -1,2 |
| 24 | 35 | 24,02 | -0,9 |
| 25 | 25 | 17,48 | -1,2 |
| 26 | 47 | 29,64 | -0,4 |
| 27 | 36 | 24,58 | -0,9 |
| 28 | 40 | 26,92 | -0,7 |
| 29 | 32 | 23,06 | -0,9 |
| 30 | 26 | 19,72 | -1,0 |
| 31 | 34 | 23,32 | -1,0 |
| 32 | 42 | 27,52 | -0,7 |
| 33 | 37 | 25,62 | -0,8 |
| 34 | 26 | 18,72 | -1,1 |
| 35 | 42 | 27,64 | -0,6 |
| 36 | 24 | 17,66 | -1,1 |
| 37 | 13 | 8,78 | -1,2 |
| 38 | 11 | 8,58 | -1,1 |
| 39 | 26 | 18,04 | -1,2 |
| 40 | 40 | 26,54 | -0,8 |
| 41 | 30 | 21,86 | -1,0 |
| 42 | 33 | 23,22 | -1,0 |
| 43 | 21 | 15,24 | -1,2 |
| 44 | 34 | 22,78 | -1,1 |
| 45 | 33 | 23,04 | -1,0 |
| 46 | 33 | 23,54 | -0,9 |
| 47 | 35 | 24,64 | -0,8 |
| 48 | 31 | 22 | -1,0 |
| 49 | 24 | 17,56 | -1,2 |
| 50 | 33 | 23,12 | -1,0 |
ВЫВОД: Учитывая, что коэффициенты дискриминации могут принимать значения от +1до -1, то задания под номерами 2, 3, 4, 7, 10, 11, 12, 13, 15, 20, 23, 25, 34, 36, 37, 38, 39, 43, 44 , 49 рассматриваются как непригодные и исключаются.
3.2 Вычисление индекса дискриминации
Индекс дискриминации – это разность между числом испытуемых, выполнивших данное задание "правильно" в «высокой» контрастной группе и числом испытуемых, выполнивших данное задание "правильно" в «низкой» контрастной группе и деленные на объемы контрастных групп.
Для вычисления индекса дискриминации используем следующую формулу:
D = (N![]()
![]() /N
/N![]()
![]() )- (N
)- (N![]()
![]() /N
/N![]()
![]() ) ,где
) ,где
D – индекс дискриминации,
N+![]() , N+
, N+![]() -числа испытуемых, выполнивших данное задание в
«высокой» и «низкой» контрольной группах.
-числа испытуемых, выполнивших данное задание в
«высокой» и «низкой» контрольной группах.
N![]() , N
, N![]() - это объёмы контрольных групп.
- это объёмы контрольных групп.
Существует несколько подходов для выбора крайних групп:
1) количество испытуемых в крайних группах одинаково (берут по 27% от общего количества испытуемых);
2) берут группы с высоким и низким показателем испытуемых, после чего считается количество испытуемых, попавших в группы.
Для вычисления объёма контрольной группы воспользуемся первым подходом, то есть «отсекаем» по 27% испытуемых из групп с «высокими» и «низкими» показателями из общего числа испытуемых.
N![]() =0,27*50=13,5 ≈ 14;
=0,27*50=13,5 ≈ 14;
N![]() =0,27*50=13,5 ≈ 14;
=0,27*50=13,5 ≈ 14;
В «высокую» контрольную группу входят испытуемые под номерами:1, 2, 3, 12, 14, 15, 16, 18, 24, 31, 32, 35, 36, 50.
В «низкую» контрольную группу входят испытуемые под номерами: 6, 9, 17, 22, 27, 30, 34, 37, 39, 40, 45, 46, 48, 49.
Результаты вычисления индекса дискриминации сведены в таблицу 6.
Таблица 6.
|
i |
N+max |
N+min |
D |
| 1 | 14 | 10 | 0,28 |
| 2 | 5 | 3 | 0,14 |
| 3 | 10 | 4 | 0,42 |
| 4 | 13 | 8 | 0,31 |
| 5 | 12 | 8 | 0,28 |
| 6 | 13 | 11 | 0,14 |
| 7 | 12 | 10 | 0,14 |
| 8 | 14 | 10 | 0,28 |
| 9 | 11 | 8 | 0,21 |
| 10 | 8 | 2 | 0,42 |
| 11 | 10 | 5 | 0,35 |
| 12 | 6 | 1 | 0,35 |
| 13 | 11 | 4 | 0,50 |
| 14 | 14 | 8 | 0,42 |
| 15 | 12 | 7 | 0,35 |
| 16 | 12 | 0 | 0,85 |
| 17 | 12 | 10 | 0,14 |
| 18 | 6 | 1 | 0,35 |
| 19 | 14 | 3 | 0,78 |
| 20 | 12 | 1 | 0,78 |
| 21 | 14 | 3 | 0,78 |
| 22 | 12 | 4 | 0,57 |
| 23 | 10 | 4 | 0,42 |
| 24 | 14 | 5 | 0,64 |
| 25 | 8 | 4 | 0,28 |
| 26 | 14 | 12 | 0,14 |
| 27 | 14 | 5 | 0,64 |
| 28 | 14 | 7 | 0,50 |
| 29 | 14 | 2 | 0,85 |
| 30 | 13 | 0 | 0,92 |
| 31 | 12 | 5 | 0,50 |
| 32 | 14 | 9 | 0,35 |
| 33 | 14 | 5 | 0,64 |
| 34 | 12 | 2 | 0,71 |
| 35 | 14 | 8 | 0,42 |
| 36 | 10 | 2 | 0,57 |
| 37 | 4 | 3 | 0,07 |
| 38 | 7 | 1 | 0,42 |
| 39 | 9 | 3 | 0,42 |
| 40 | 14 | 7 | 0,50 |
| 41 | 14 | 2 | 0,85 |
| 42 | 12 | 4 | 0,57 |
| 43 | 13 | 3 | 0,71 |
| 44 | 12 | 7 | 0,35 |
| 45 | 14 | 4 | 0,71 |
| 46 | 13 | 3 | 0,71 |
| 47 | 14 | 3 | 0,78 |
| 48 | 12 | 2 | 0,71 |
| 49 | 12 | 2 | 0,71 |
| 50 | 14 | 4 | 0,71 |
Обычно индекс дискриминации принимает знач.от -1 до +1, чем выше индекс дискриминации, тем выше дискриминативность задания.
Если D близко к 1, значит, задание хорошо разделяет испытуемых на «слабых» и «сильных».
Если D<0 , то необходимо удалить задание из теста.
Если D близко к нулю, значит задание некорректно сформулировано.
В идеале D>=0,2 и D<1
Задания, не соответствующие требованию удаляются из опросника, т.е.удаляем из опросника задания под номерами 2, 6, 7, 17, 26, 37.
4. ОПРЕДЕЛЕНИЕ НАДЁЖНОСТИ ТЕСТА
Надёжность - устойчивость результатов, которые получены при помощи теста. Надежность – это один из критериев качества теста, относящийся к точности психологических измерений. Чем больше надежность теста, тем относительно свободнее он от погрешностей измерения.
Обычно тест считается надёжным, если с его помощью получаются одни и те же показатели для каждого испытуемого при повторном тестировании/исследовании. Существует несколько способов определения надёжности.
4.1 Определение надёжности целого теста
Надёжность ретестовая предполагает повторное предъявление того же самого теста тем же самым испытуемым в тех же условиях, а затем установление корреляции между двумя рядами данных. Повторное испытание проводилось через месяц.
Для вычисления надёжности целого теста необходимо произвести вычисления:
- Определяем стандартное отклонение первого испытания:
Sx=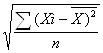 , где
, где
Sx-стандартное отклонение индивидуальных оценок всех испытуемых выборки для первого испытания,
Xi- индивидуальный балл каждого испытуемого по всему тесту для первого испытания,
![]() - среднее арифметическое оценок по
всему тесту всех испытуемых для первого испытания,
- среднее арифметическое оценок по
всему тесту всех испытуемых для первого испытания,
n-общее количество испытуемых, для первого испытания;
Стандартное отклонение первого испытания было определено нами ранее и составляет
Sx=10,538
- Теперь вычисляем стандартное отклонение второго испытания:
Sy= ,где
,где
Sу-стандартное отклонение индивидуальных оценок всех испытуемых выборки для второго испытания,
Yi- индивидуальный балл каждого испытуемого по всему тесту для второго испытания,
![]() - среднее арифметическое оценок по
всему тесту всех испытуемых для второго испытания,
- среднее арифметическое оценок по
всему тесту всех испытуемых для второго испытания, ![]() =
=![]()
Результаты вычисления стандартного отклонения всех испытуемых для второго испытания сведено в таблицу 7.
Таблица 7
|
i |
Yi |
|
|
| 1 | 45 | 13,02 | 169,5204 |
| 2 | 43 | 11,02 | 121,4404 |
| 3 | 41 | 9,02 | 81,3604 |
| 4 | 34 | 2,02 | 4,0804 |
| 5 | 35 | 3,02 | 9,1204 |
| 6 | 23 | -8,98 | 80,6404 |
| 7 | 26 | -5,98 | 35,7604 |
| 8 | 29 | -2,98 | 8,8804 |
| 9 | 21 | -10,98 | 120,5604 |
| 10 | 38 | 6,02 | 36,2404 |
| 11 | 42 | 10,02 | 100,4004 |
| 12 | 40 | 8,02 | 64,3204 |
| 13 | 34 | 2,02 | 4,0804 |
| 14 | 44 | 12,02 | 144,4804 |
| 15 | 40 | 8,02 | 64,3204 |
| 16 | 45 | 13,02 | 169,5204 |
| 17 | 18 | -13,98 | 195,4404 |
| 18 | 47 | 15,02 | 225,6004 |
| 19 | 38 | 6,02 | 36,2404 |
| 20 | 35 | 3,02 | 9,1204 |
| 21 | 28 | -3,98 | 15,8404 |
| 22 | 20 | -11,98 | 143,5204 |
| 23 | 26 | -5,98 | 35,7604 |
| 24 | 38 | 6,02 | 36,2404 |
| 25 | 43 | 11,02 | 121,4404 |
| 26 | 32 | 0,02 | 0,0004 |
| 27 | 16 | -15,98 | 255,3604 |
| 28 | 42 | 10,02 | 100,4004 |
| 29 | 38 | 6,02 | 36,2404 |
| 30 | 24 | -7,98 | 63,6804 |
| 31 | 40 | 8,02 | 64,3204 |
| 32 | 47 | 15,02 | 225,6004 |
| 33 | 37 | 5,02 | 25,2004 |
| 34 | 20 | -11,98 | 143,5204 |
| 35 | 40 | 8,02 | 64,3204 |
| 36 | 44 | 12,02 | 144,4804 |
| 37 | 19 | -12,98 | 168,4804 |
| 38 | 29 | -2,98 | 8,8804 |
| 39 | 18 | -13,98 | 195,4404 |
| 40 | 19 | -12,98 | 168,4804 |
| 41 | 29 | -2,98 | 8,8804 |
| 42 | 28 | -3,98 | 15,8404 |
| 43 | 35 | 3,02 | 9,1204 |
| 44 | 33 | 1,02 | 1,0404 |
| 45 | 19 | -12,98 | 168,4804 |
| 46 | 17 | -14,98 | 224,4004 |
| 47 | 25 | -6,98 | 48,7204 |
| 48 | 18 | -13,98 | 195,4404 |
| 49 | 18 | -13,98 | 195,4404 |
| 50 | 39 | 7,02 | 49,2804 |
|
|
4614,98 |
n-общее количество испытуемых, для первого испытания;
Таким образом:
Sy= =
=![]() =9,705
=9,705
- Затем вычисляем коэффициент корреляции между двумя тестовыми испытаниями, для этого используем формулу коэффициента корреляции произведений моментов Пирсона:
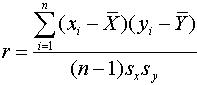
Воспользуемся следующей таблицей.
Таблица 8
|
i |
Xi |
|
Yi |
|
|
| 1 | 46 | 15,18 | 45 | 13,02 | 197,6436 |
| 2 | 43 | 12,18 | 43 | 11,02 | 134,2236 |
| 3 | 40 | 9,18 | 41 | 9,02 | 82,8036 |
| 4 | 30 | -0,82 | 34 | 2,02 | -1,6564 |
| 5 | 35 | 4,18 | 35 | 3,02 | 12,6236 |
| 6 | 17 | -13,82 | 23 | -8,98 | 124,1036 |
| 7 | 27 | -3,82 | 26 | -5,98 | 22,8436 |
| 8 | 22 | -8,82 | 29 | -2,98 | 26,2836 |
| 9 | 18 | -12,82 | 21 | -10,98 | 140,7636 |
| 10 | 38 | 7,18 | 38 | 6,02 | 43,2236 |
| 11 | 42 | 11,18 | 42 | 10,02 | 112,0236 |
| 12 | 39 | 8,18 | 40 | 8,02 | 65,6036 |
| 13 | 32 | 1,18 | 34 | 2,02 | 2,3836 |
| 14 | 45 | 14,18 | 44 | 12,02 | 170,4436 |
| 15 | 39 | 8,18 | 40 | 8,02 | 65,6036 |
| 16 | 44 | 13,18 | 45 | 13,02 | 171,6036 |
| 17 | 15 | -15,82 | 18 | -13,98 | 221,1636 |
| 18 | 47 | 16,18 | 47 | 15,02 | 243,0236 |
| 19 | 36 | 5,18 | 38 | 6,02 | 31,1836 |
| 20 | 35 | 4,18 | 35 | 3,02 | 12,6236 |
| 21 | 28 | -2,82 | 28 | -3,98 | 11,2236 |
| 22 | 16 | -14,82 | 20 | -11,98 | 177,5436 |
| 23 | 26 | -4,82 | 26 | -5,98 | 28,8236 |
| 24 | 38 | 7,18 | 38 | 6,02 | 43,2236 |
| 25 | 42 | 11,18 | 43 | 11,02 | 123,2036 |
| 26 | 30 | -0,82 | 32 | 0,02 | -0,0164 |
| 27 | 13 | -17,82 | 16 | -15,98 | 284,7636 |
| 28 | 43 | 12,18 | 42 | 10,02 | 122,0436 |
| 29 | 36 | 5,18 | 38 | 6,02 | 31,1836 |
| 30 | 21 | -9,82 | 24 | -7,98 | 78,3636 |
| 31 | 40 | 9,18 | 40 | 8,02 | 73,6236 |
| 32 | 48 | 17,18 | 47 | 15,02 | 258,0436 |
| 33 | 36 | 5,18 | 37 | 5,02 | 26,0036 |
| 34 | 18 | -12,82 | 20 | -11,98 | 153,5836 |
| 35 | 40 | 9,18 | 40 | 8,02 | 73,6236 |
| 36 | 43 | 12,18 | 44 | 12,02 | 146,4036 |
| 37 | 17 | -13,82 | 19 | -12,98 | 179,3836 |
| 38 | 27 | -3,82 | 29 | -2,98 | 11,3836 |
| 39 | 15 | -15,82 | 18 | -13,98 | 221,1636 |
| 40 | 19 | -11,82 | 19 | -12,98 | 153,4236 |
| 41 | 29 | -1,82 | 29 | -2,98 | 5,4236 |
| 42 | 26 | -4,82 | 28 | -3,98 | 19,1836 |
| 43 | 34 | 3,18 | 35 | 3,02 | 9,6036 |
| 44 | 32 | 1,18 | 33 | 1,02 | 1,2036 |
| 45 | 19 | -11,82 | 19 | -12,98 | 153,4236 |
| 46 | 16 | -14,82 | 17 | -14,98 | 222,0036 |
| 47 | 25 | -5,82 | 25 | -6,98 | 40,6236 |
| 48 | 17 | -13,82 | 18 | -13,98 | 193,2036 |
| 49 | 18 | -12,82 | 18 | -13,98 | 179,2236 |
| 50 | 39 | 8,18 | 39 | 7,02 | 57,4236 |
|
∑ |
4956,82 |
Коэффициент корреляции между двумя испытаниями равен
r=4956, 82/ ((50-1)*10,538*9,705) = 0,989
Чем ближе к 1 значение r, тем выше надёжность теста.
Минимальное значение коэффициента корреляции равно 0,7.
Тем самым примерно 98% испытуемых выполнили задание с теми самыми значениями. Это говорит о достаточной высокой надежности разработанного теста.
4.2 Определение надёжности частей теста
Надёжность частей теста определяется сопоставлением результатов тестирования по двум эквивалентным частям теста. «Разбиваем» наш тест на 2 одинаковый части по принципу деления на чётные и нечётные номера заданий.
Всех испытуемых мы протестируем сначала по одной части теста, а затем по другой.
После тестирования вычислим коэффициент корреляции:
- Сначала
вычисляем стандартные отклонения (![]() 1 и
1 и ![]() 2) для половин теста:
2) для половин теста:
![]() 1=
1=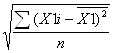 , где
, где
X1i- общий балл, полученный каждым испытуемым по первой половине теста,
![]() - это среднее арифметическое баллов, полученных
всеми испытуемыми по первой половине теста.
- это среднее арифметическое баллов, полученных
всеми испытуемыми по первой половине теста.
![]() 2=
2=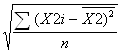 , где
, где
X2i- общий балл, полученный каждым испытуемым по второй половине теста,
![]() - это среднее арифметическое баллов,
полученных всеми испытуемыми по второй половине теста.
- это среднее арифметическое баллов,
полученных всеми испытуемыми по второй половине теста.
Значения X1i и X2i по четной и нечетной частям теста приведено в таблице 9.
Таблица 9
|
i |
X1i |
X2i |
| 1 | 24 | 22 |
| 2 | 24 | 19 |
| 3 | 19 | 21 |
| 4 | 14 | 16 |
| 5 | 19 | 16 |
| 6 | 7 | 10 |
| 7 | 14 | 13 |
| 8 | 13 | 9 |
| 9 | 10 | 8 |
| 10 | 18 | 20 |
| 11 | 22 | 20 |
| 12 | 18 | 21 |
| 13 | 17 | 15 |
| 14 | 23 | 22 |
| 15 | 20 | 19 |
| 16 | 22 | 22 |
| 17 | 9 | 6 |
| 18 | 24 | 23 |
| 19 | 19 | 17 |
| 20 | 21 | 14 |
| 21 | 14 | 14 |
| 22 | 8 | 8 |
| 23 | 11 | 15 |
| 24 | 19 | 19 |
| 25 | 22 | 20 |
| 26 | 16 | 14 |
| 27 | 7 | 6 |
| 28 | 22 | 21 |
| 29 | 19 | 17 |
| 30 | 10 | 11 |
| 31 | 18 | 22 |
| 32 | 25 | 23 |
| 33 | 17 | 19 |
| 34 | 10 | 8 |
| 35 | 20 | 20 |
| 36 | 22 | 21 |
| 37 | 9 | 8 |
| 38 | 12 | 15 |
| 39 | 7 | 8 |
| 40 | 11 | 8 |
| 41 | 15 | 14 |
| 42 | 15 | 11 |
| 43 | 18 | 16 |
| 44 | 17 | 15 |
| 45 | 11 | 8 |
| 46 | 8 | 8 |
| 47 | 11 | 14 |
| 48 | 7 | 10 |
| 49 | 11 | 7 |
| 50 | 18 | 21 |
| ∑ | 787 | 754 |
На основании данных, приведенных в таблице
![]() =
=![]() =
=![]() =15,74;
=15,74;
![]() =
=![]() =
=![]() =15,08;
=15,08;
Для
вычисления значений ![]() 1 и
1 и ![]() 2 воспользуемся следующей
таблицей.
2 воспользуемся следующей
таблицей.
Таблица 10.
| i | X1i | X2i |
|
|
|
|
| 1 | 24 | 22 | 8,26 | 6,92 | 68,2276 | 47,8864 |
| 2 | 24 | 19 | 8,26 | 3,92 | 68,2276 | 15,3664 |
| 3 | 19 | 21 | 3,26 | 5,92 | 10,6276 | 35,0464 |
| 4 | 14 | 16 | -1,74 | 0,92 | 3,0276 | 0,8464 |
| 5 | 19 | 16 | 3,26 | 0,92 | 10,6276 | 0,8464 |
| 6 | 7 | 10 | -8,74 | -5,08 | 76,3876 | 25,8064 |
| 7 | 14 | 13 | -1,74 | -2,08 | 3,0276 | 4,3264 |
| 8 | 13 | 9 | -2,74 | -6,08 | 7,5076 | 36,9664 |
| 9 | 10 | 8 | -5,74 | -7,08 | 32,9476 | 50,1264 |
| 10 | 18 | 20 | 2,26 | 4,92 | 5,1076 | 24,2064 |
| 11 | 22 | 20 | 6,26 | 4,92 | 39,1876 | 24,2064 |
| 12 | 18 | 21 | 2,26 | 5,92 | 5,1076 | 35,0464 |
| 13 | 17 | 15 | 1,26 | -0,08 | 1,5876 | 0,0064 |
| 14 | 23 | 22 | 7,26 | 6,92 | 52,7076 | 47,8864 |
| 15 | 20 | 19 | 4,26 | 3,92 | 18,1476 | 15,3664 |
| 16 | 22 | 22 | 6,26 | 6,92 | 39,1876 | 47,8864 |
| 17 | 9 | 6 | -6,74 | -9,08 | 45,4276 | 82,4464 |
| 18 | 24 | 23 | 8,26 | 7,92 | 68,2276 | 62,7264 |
| 19 | 19 | 17 | 3,26 | 1,92 | 10,6276 | 3,6864 |
| 20 | 21 | 14 | 5,26 | -1,08 | 27,6676 | 1,1664 |
| 21 | 14 | 14 | -1,74 | -1,08 | 3,0276 | 1,1664 |
| 22 | 8 | 8 | -7,74 | -7,08 | 59,9076 | 50,1264 |
| 23 | 11 | 15 | -4,74 | -0,08 | 22,4676 | 0,0064 |
| 24 | 19 | 19 | 3,26 | 3,92 | 10,6276 | 15,3664 |
| 25 | 22 | 20 | 6,26 | 4,92 | 39,1876 | 24,2064 |
| 26 | 16 | 14 | 0,26 | -1,08 | 0,0676 | 1,1664 |
| 27 | 7 | 6 | -8,74 | -9,08 | 76,3876 | 82,4464 |
| 28 | 22 | 21 | 6,26 | 5,92 | 39,1876 | 35,0464 |
| 29 | 19 | 17 | 3,26 | 1,92 | 10,6276 | 3,6864 |
| 30 | 10 | 11 | -5,74 | -4,08 | 32,9476 | 16,6464 |
| 31 | 18 | 22 | 2,26 | 6,92 | 5,1076 | 47,8864 |
| 32 | 25 | 23 | 9,26 | 7,92 | 85,7476 | 62,7264 |
| 33 | 17 | 19 | 1,26 | 3,92 | 1,5876 | 15,3664 |
| 34 | 10 | 8 | -5,74 | -7,08 | 32,9476 | 50,1264 |
| 35 | 20 | 20 | 4,26 | 4,92 | 18,1476 | 24,2064 |
| 36 | 22 | 21 | 6,26 | 5,92 | 39,1876 | 35,0464 |
| 37 | 9 | 8 | -6,74 | -7,08 | 45,4276 | 50,1264 |
| 38 | 12 | 15 | -3,74 | -0,08 | 13,9876 | 0,0064 |
| 39 | 7 | 8 | -8,74 | -7,08 | 76,3876 | 50,1264 |
| 40 | 11 | 8 | -4,74 | -7,08 | 22,4676 | 50,1264 |
| 41 | 15 | 14 | -0,74 | -1,08 | 0,5476 | 1,1664 |
| 42 | 15 | 11 | -0,74 | -4,08 | 0,5476 | 16,6464 |
| 43 | 18 | 16 | 2,26 | 0,92 | 5,1076 | 0,8464 |
| 44 | 17 | 15 | 1,26 | -0,08 | 1,5876 | 0,0064 |
| 45 | 11 | 8 | -4,74 | -7,08 | 22,4676 | 50,1264 |
| 46 | 8 | 8 | -7,74 | -7,08 | 59,9076 | 50,1264 |
| 47 | 11 | 14 | -4,74 | -1,08 | 22,4676 | 1,1664 |
| 48 | 7 | 10 | -8,74 | -5,08 | 76,3876 | 25,8064 |
| 49 | 11 | 7 | -4,74 | -8,08 | 22,4676 | 65,2864 |
| 50 | 18 | 21 | 2,26 | 5,92 | 5,1076 | 35,0464 |
| ∑ | 1445,62 | 1423,68 |
На основании приведенных данных:
![]() 1=
1=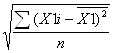 =
=![]()
![]() =5,36;
=5,36;
![]() 2=
2=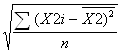 =
=![]() =5,34;
=5,34;
Поскольку ![]() 1≈
1≈![]() 2, то коэффициент надёжности
целого теста вычисляется по формуле:
2, то коэффициент надёжности
целого теста вычисляется по формуле:
r![]() =
=![]() , где
, где
r – коэффициент надёжности половин теста, вычисляемый по формуле:
![]() , где
, где
X- общий балл, полученный каждым испытуемым по первой половине теста,
![]() - это среднее арифметическое баллов,
полученных всеми испытуемыми по первой половине теста.
- это среднее арифметическое баллов,
полученных всеми испытуемыми по первой половине теста.
Y- общий балл, полученный каждым испытуемым по второй половине теста,
![]() - это среднее арифметическое баллов,
полученных всеми испытуемыми по второй половине теста.
- это среднее арифметическое баллов,
полученных всеми испытуемыми по второй половине теста.
Все исходные данные для вычисления коэффициента надёжности половин теста приведены в таблице 10.
На основании приведенных данных коэффициент надежности половин теста равен:
r=![]() =
=![]() =0,76
=0,76
Соответственно,
r![]() =
=![]() =
=![]() =
=![]() =0,86
=0,86
Обычно, если значения коэффициента rxx попадают в интервал 0,80-0,89, то говорят, что тест обладает хорошей надежностью, а если этот коэффициент не меньше 0,90, то надежность можно назвать очень высокой.
5. ОПРЕДЕЛЕНИЕ ВАЛИДНОСТИ ТЕСТА
Валидность теста показывает, насколько хорошо тест делает то, для чего он был создан. Определить коэффициент валидности теста – значит определить, как выполнение теста соотносится с другими независимо сделанными оценками знаний испытуемых.
Валидация – это улучшение качеств теста, например, после сопоставления результатов по тестам и нетестовым формам контроля.
Валидность измеряется коэффициентом валидности. Это число между 0 и 1, которое степень близости «r» между тестом и мерой выполнения «работы» (критерием). Чем больше значение коэффициента, тем более вы можете быть уверенны в предсказаниях, основанных на тестовом балле. Тем ни менее, один тест никогда не может полностью предсказать степень исполнения «работы», так как слишком много различных факторов влияют на успех в «работе». Поэтому коэффициент валидности, в отличии от коэффициентов надежности, редко превышает r = 0.40.
В данном случае нами будет рассчитываться валидность путем нахождения коэффициента корреляции между результатами тестирования разработанной нами методикой и другой методикой, исследующей данный конструкт, с доказанной валидностью. Для этого используем формулу коэффициента корреляции Пирсона:
r![]() =
=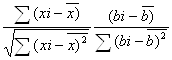
![]() ,
где
,
где
bi – результат каждого испытуемого по валидному тесту.
Подробные вычисления коэффициента корреляции Пирсона сведем в таблицу 11.
Таблица 11.
|
i |
Xi |
bi |
Xi-X |
Bi-B |
(Xi-X)^2 |
(Bi-B)^2 |
| 1 | 46 | 44 | 15,18 | 9,36 | 230,4324 | 87,6096 |
| 2 | 43 | 42 | 12,18 | 7,36 | 148,3524 | 54,1696 |
| 3 | 40 | 42 | 9,18 | 7,36 | 84,2724 | 54,1696 |
| 4 | 30 | 36 | -0,82 | 1,36 | 0,6724 | 1,8496 |
| 5 | 35 | 40 | 4,18 | 5,36 | 17,4724 | 28,7296 |
| 6 | 17 | 36 | -13,82 | 1,36 | 190,9924 | 1,8496 |
| 7 | 27 | 32 | -3,82 | -2,64 | 14,5924 | 6,9696 |
| 8 | 22 | 32 | -8,82 | -2,64 | 77,7924 | 6,9696 |
| 9 | 18 | 27 | -12,82 | -7,64 | 164,3524 | 58,3696 |
| 10 | 38 | 44 | 7,18 | 9,36 | 51,5524 | 87,6096 |
| 11 | 42 | 47 | 11,18 | 12,36 | 124,9924 | 152,7696 |
| 12 | 39 | 39 | 8,18 | 4,36 | 66,9124 | 19,0096 |
| 13 | 32 | 35 | 1,18 | 0,36 | 1,3924 | 0,1296 |
| 14 | 45 | 46 | 14,18 | 11,36 | 201,0724 | 129,0496 |
| 15 | 39 | 42 | 8,18 | 7,36 | 66,9124 | 54,1696 |
| 16 | 44 | 42 | 13,18 | 7,36 | 173,7124 | 54,1696 |
| 17 | 15 | 29 | -15,82 | -5,64 | 250,2724 | 31,8096 |
| 18 | 47 | 49 | 16,18 | 14,36 | 261,7924 | 206,2096 |
| 19 | 36 | 42 | 5,18 | 7,36 | 26,8324 | 54,1696 |
| 20 | 35 | 36 | 4,18 | 1,36 | 17,4724 | 1,8496 |
| 21 | 28 | 32 | -2,82 | -2,64 | 7,9524 | 6,9696 |
| 22 | 16 | 28 | -14,82 | -6,64 | 219,6324 | 44,0896 |
| 23 | 26 | 28 | -4,82 | -6,64 | 23,2324 | 44,0896 |
| 24 | 38 | 38 | 7,18 | 3,36 | 51,5524 | 11,2896 |
| 25 | 42 | 44 | 11,18 | 9,36 | 124,9924 | 87,6096 |
| 26 | 30 | 35 | -0,82 | 0,36 | 0,6724 | 0,1296 |
| 27 | 13 | 18 | -17,82 | -16,64 | 317,5524 | 276,8896 |
| 28 | 43 | 42 | 12,18 | 7,36 | 148,3524 | 54,1696 |
| 29 | 36 | 40 | 5,18 | 5,36 | 26,8324 | 28,7296 |
| 30 | 21 | 26 | -9,82 | -8,64 | 96,4324 | 74,6496 |
| 31 | 40 | 38 | 9,18 | 3,36 | 84,2724 | 11,2896 |
| 32 | 48 | 45 | 17,18 | 10,36 | 295,1524 | 107,3296 |
| 33 | 36 | 40 | 5,18 | 5,36 | 26,8324 | 28,7296 |
| 34 | 18 | 26 | -12,82 | -8,64 | 164,3524 | 74,6496 |
| 35 | 40 | 44 | 9,18 | 9,36 | 84,2724 | 87,6096 |
| 36 | 43 | 42 | 12,18 | 7,36 | 148,3524 | 54,1696 |
| 37 | 17 | 23 | -13,82 | -11,64 | 190,9924 | 135,4896 |
| 38 | 27 | 33 | -3,82 | -1,64 | 14,5924 | 2,6896 |
| 39 | 15 | 25 | -15,82 | -9,64 | 250,2724 | 92,9296 |
| 40 | 19 | 28 | -11,82 | -6,64 | 139,7124 | 44,0896 |
| 41 | 29 | 30 | -1,82 | -4,64 | 3,3124 | 21,5296 |
| 42 | 26 | 31 | -4,82 | -3,64 | 23,2324 | 13,2496 |
| 43 | 34 | 33 | 3,18 | -1,64 | 10,1124 | 2,6896 |
| 44 | 32 | 35 | 1,18 | 0,36 | 1,3924 | 0,1296 |
| 45 | 19 | 24 | -11,82 | -10,64 | 139,7124 | 113,2096 |
| 46 | 16 | 18 | -14,82 | -16,64 | 219,6324 | 276,8896 |
| 47 | 25 | 26 | -5,82 | -8,64 | 33,8724 | 74,6496 |
| 48 | 17 | 24 | -13,82 | -10,64 | 190,9924 | 113,2096 |
| 49 | 18 | 18 | -12,82 | -16,64 | 164,3524 | 276,8896 |
| 50 | 39 | 36 | 8,18 | 1,36 | 66,9124 | 1,8496 |
| ∑ | 1541 | 1732 | 49,75 | 35,52 | 5441,38 | 3253,52 |
Таким образом,
r![]() =
=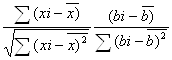 =
=![]() =
=![]() = 0, 4
= 0, 4
Наши исследования показали, что тест имеет высокий коэффициент валидности, что может свидетельствовать, что разработанный нами тест вполне может быть признан валидным и использоваться в практике.
6. СТАНДАРТИЗАЦИЯ ПОКАЗАТЕЛЕЙ (Z-ПРЕОБРАЗОВАНИЕ ОЦЕНОК)
Стандартизация – этhttp://voluntary.ru/dictionary/662/word/%D0%C0%D1%D7%C5%D2о расчет нескольких сравниваемых совокупностей в целях исключения влияния структур на величину изучаемого показателя и приведения данных к сопоставимому виду.
Стандартизация показаний позволяет сравнить показатели, полученные испытуемым с таковыми в генеральной совокупности. В данном случае стандартизированные показатели мы получаем с помощью линейного преобразования первичных показателей (сырых данных).
В этом случае показатели называются Z-стандартными и вычисляются по формуле:
![]() , где
, где
Xi- индивидуальный балл каждого испытуемого по всему тесту,
![]() - среднее арифметическое оценок по
всему тесту всех испытуемых,
- среднее арифметическое оценок по
всему тесту всех испытуемых, ![]() =30,82;
=30,82;
![]() =Sx - стандартное отклонение индивидуальных оценок всех
испытуемых выборки, данное отклонение было рассчитано нами ранее и составляет
10,538;
=Sx - стандартное отклонение индивидуальных оценок всех
испытуемых выборки, данное отклонение было рассчитано нами ранее и составляет
10,538;
Результаты расчета Z-показателей для всех испытуемых сведем в таблицу 12.
Таблица 12
|
i |
Xi |
|
Z |
| 1 | 46 | 15,18 | 1,44 |
| 2 | 43 | 12,18 | 1,16 |
| 3 | 40 | 9,18 | 0,87 |
| 4 | 30 | -0,82 | -0,08 |
| 5 | 35 | 4,18 | 0,40 |
| 6 | 17 | -13,82 | -1,31 |
| 7 | 27 | -3,82 | -0,36 |
| 8 | 22 | -8,82 | -0,84 |
| 9 | 18 | -12,82 | -1,22 |
| 10 | 38 | 7,18 | 0,68 |
| 11 | 42 | 11,18 | 1,06 |
| 12 | 39 | 8,18 | 0,78 |
| 13 | 32 | 1,18 | 0,11 |
| 14 | 45 | 14,18 | 1,35 |
| 15 | 39 | 8,18 | 0,78 |
| 16 | 44 | 13,18 | 1,25 |
| 17 | 15 | -15,82 | -1,50 |
| 18 | 47 | 16,18 | 1,54 |
| 19 | 36 | 5,18 | 0,49 |
| 20 | 35 | 4,18 | 0,40 |
| 21 | 28 | -2,82 | -0,27 |
| 22 | 16 | -14,82 | -1,41 |
| 23 | 26 | -4,82 | -0,46 |
| 24 | 38 | 7,18 | 0,68 |
| 25 | 42 | 11,18 | 1,06 |
| 26 | 30 | -0,82 | -0,08 |
| 27 | 13 | -17,82 | -1,69 |
| 28 | 43 | 12,18 | 1,16 |
| 29 | 36 | 5,18 | 0,49 |
| 30 | 21 | -9,82 | -0,93 |
| 31 | 40 | 9,18 | 0,87 |
| 32 | 48 | 17,18 | 1,63 |
| 33 | 36 | 5,18 | 0,49 |
| 34 | 18 | -12,82 | -1,22 |
| 35 | 40 | 9,18 | 0,87 |
| 36 | 43 | 12,18 | 1,16 |
| 37 | 17 | -13,82 | -1,31 |
| 38 | 27 | -3,82 | -0,36 |
| 39 | 15 | -15,82 | -1,50 |
| 40 | 19 | -11,82 | -1,12 |
| 41 | 29 | -1,82 | -0,17 |
| 42 | 26 | -4,82 | -0,46 |
| 43 | 34 | 3,18 | 0,30 |
| 44 | 32 | 1,18 | 0,11 |
| 45 | 19 | -11,82 | -1,12 |
| 46 | 16 | -14,82 | -1,41 |
| 47 | 25 | -5,82 | -0,55 |
| 48 | 17 | -13,82 | -1,31 |
| 49 | 18 | -12,82 | -1,22 |
| 50 | 39 | 8,18 | 0,78 |
После получения стандартного балла Z можно перевести тестовый балл испытуемого в любую стандартную тестовую шкалу, например в шкалу стенов. Формула пересчета выглядит следующим образом:
![]()
Результаты расчета приведем в таблице 13.
Таблица 13.
|
i |
Xi |
Xi-X |
Z |
Y |
| 1 | 46 | 15,18 | 1,44 | 7 |
| 2 | 43 | 12,18 | 1,16 | 7 |
| 3 | 40 | 9,18 | 0,87 | 6 |
| 4 | 30 | -0,82 | -0,08 | 5 |
| 5 | 35 | 4,18 | 0,40 | 6 |
| 6 | 17 | -13,82 | -1,31 | 4 |
| 7 | 27 | -3,82 | -0,36 | 5 |
| 8 | 22 | -8,82 | -0,84 | 5 |
| 9 | 18 | -12,82 | -1,22 | 4 |
| 10 | 38 | 7,18 | 0,68 | 6 |
| 11 | 42 | 11,18 | 1,06 | 7 |
| 12 | 39 | 8,18 | 0,78 | 6 |
| 13 | 32 | 1,18 | 0,11 | 6 |
| 14 | 45 | 14,18 | 1,35 | 7 |
| 15 | 39 | 8,18 | 0,78 | 6 |
| 16 | 44 | 13,18 | 1,25 | 7 |
| 17 | 15 | -15,82 | -1,50 | 4 |
| 18 | 47 | 16,18 | 1,54 | 7 |
| 19 | 36 | 5,18 | 0,49 | 6 |
| 20 | 35 | 4,18 | 0,40 | 6 |
| 21 | 28 | -2,82 | -0,27 | 5 |
| 22 | 16 | -14,82 | -1,41 | 4 |
| 23 | 26 | -4,82 | -0,46 | 5 |
| 24 | 38 | 7,18 | 0,68 | 6 |
| 25 | 42 | 11,18 | 1,06 | 7 |
| 26 | 30 | -0,82 | -0,08 | 5 |
| 27 | 13 | -17,82 | -1,69 | 4 |
| 28 | 43 | 12,18 | 1,16 | 7 |
| 29 | 36 | 5,18 | 0,49 | 6 |
| 30 | 21 | -9,82 | -0,93 | 5 |
| 31 | 40 | 9,18 | 0,87 | 6 |
| 32 | 48 | 17,18 | 1,63 | 7 |
| 33 | 36 | 5,18 | 0,49 | 6 |
| 34 | 18 | -12,82 | -1,22 | 4 |
| 35 | 40 | 9,18 | 0,87 | 6 |
| 36 | 43 | 12,18 | 1,16 | 7 |
| 37 | 17 | -13,82 | -1,31 | 4 |
| 38 | 27 | -3,82 | -0,36 | 5 |
| 39 | 15 | -15,82 | -1,50 | 4 |
| 40 | 19 | -11,82 | -1,12 | 4 |
| 41 | 29 | -1,82 | -0,17 | 5 |
| 42 | 26 | -4,82 | -0,46 | 5 |
| 43 | 34 | 3,18 | 0,30 | 6 |
| 44 | 32 | 1,18 | 0,11 | 6 |
| 45 | 19 | -11,82 | -1,12 | 4 |
| 46 | 16 | -14,82 | -1,41 | 4 |
| 47 | 25 | -5,82 | -0,55 | 5 |
| 48 | 17 | -13,82 | -1,31 | 4 |
| 49 | 18 | -12,82 | -1,22 | 4 |
| 50 | 39 | 8,18 | 0,78 | 6 |
7. ВЫЧИСЛЕНИЕ АССИМЕТРИИ И ЭКСЦЕССА ЭМПИРИЧЕСКОГО РАСПРЕДЕЛЕНИЯ
Для определения характера эмпирического распределения и степени его согласованности с нормальным мы используем следующую формулу:
А=![]() , где
, где
Xi- индивидуальный балл каждого испытуемого по всему тесту,
![]() - среднее арифметическое оценок по
всему тесту всех испытуемых,
- среднее арифметическое оценок по
всему тесту всех испытуемых, ![]() =30,82;
=30,82;
![]() =Sx - стандартное отклонение индивидуальных оценок всех
испытуемых выборки, данное отклонение было рассчитано нами ранее и составляет
10,538;
=Sx - стандартное отклонение индивидуальных оценок всех
испытуемых выборки, данное отклонение было рассчитано нами ранее и составляет
10,538;
n – количество испытуемых, n=50;
Тогда, сведем все промежуточные результаты расчетов в таблицу 14.
Таблица 14
|
i |
Xi |
|
|
| 1 | 46 | 15,18 | 3497,96 |
| 2 | 43 | 12,18 | 1806,93 |
| 3 | 40 | 9,18 | 773,62 |
| 4 | 30 | -0,82 | -0,55 |
| 5 | 35 | 4,18 | 73,03 |
| 6 | 17 | -13,82 | -2639,51 |
| 7 | 27 | -3,82 | -55,74 |
| 8 | 22 | -8,82 | -686,13 |
| 9 | 18 | -12,82 | -2107,00 |
| 10 | 38 | 7,18 | 370,15 |
| 11 | 42 | 11,18 | 1397,42 |
| 12 | 39 | 8,18 | 547,34 |
| 13 | 32 | 1,18 | 1,64 |
| 14 | 45 | 14,18 | 2851,21 |
| 15 | 39 | 8,18 | 547,34 |
| 16 | 44 | 13,18 | 2289,53 |
| 17 | 15 | -15,82 | -3959,31 |
| 18 | 47 | 16,18 | 4235,80 |
| 19 | 36 | 5,18 | 138,99 |
| 20 | 35 | 4,18 | 73,03 |
| 21 | 28 | -2,82 | -22,43 |
| 22 | 16 | -14,82 | -3254,95 |
| 23 | 26 | -4,82 | -111,98 |
| 24 | 38 | 7,18 | 370,14 |
| 25 | 42 | 11,18 | 1397,41 |
| 26 | 30 | -0,82 | -0,55 |
| 27 | 13 | -17,82 | -5658,78 |
| 28 | 43 | 12,18 | 1806,93 |
| 29 | 36 | 5,18 | 138,99 |
| 30 | 21 | -9,82 | -946,97 |
| 31 | 40 | 9,18 | 773,62 |
| 32 | 48 | 17,18 | 5070,71 |
| 33 | 36 | 5,18 | 138,99 |
| 34 | 18 | -12,82 | -2107,00 |
| 35 | 40 | 9,18 | 773,62 |
| 36 | 43 | 12,18 | 1806,93 |
| 37 | 17 | -13,82 | -2639,51 |
| 38 | 27 | -3,82 | -55,743 |
| 39 | 15 | -15,82 | -3959,31 |
| 40 | 19 | -11,82 | -1651,40 |
| 41 | 29 | -1,82 | -6,03 |
| 42 | 26 | -4,82 | -111,98 |
| 43 | 34 | 3,18 | 32,16 |
| 44 | 32 | 1,18 | 1,64 |
| 45 | 19 | -11,82 | -1651,40 |
| 46 | 16 | -14,82 | -3254,95 |
| 47 | 25 | -5,82 | -197,14 |
| 48 | 17 | -13,82 | -2639,51 |
| 49 | 18 | -12,82 | -2107,00 |
| 50 | 39 | 8,18 | 547,34 |
| ∑ | -8362,36 |
А=![]() =
= ![]() =
=![]() = -0,14
= -0,14
Таким образом, ассиметрия полученного нами эмпирического распределения равна -0,14
Е=![]()
Результаты вычисления снова сведем в таблицу.
Таблица 15
|
i |
Xi |
|
|
| 1 | 46 | 15,18 | 53099,09 |
| 2 | 43 | 12,18 | 22008,43 |
| 3 | 40 | 9,18 | 7101,84 |
| 4 | 30 | -0,82 | 0,45 |
| 5 | 35 | 4,18 | 305,28 |
| 6 | 17 | -13,82 | 36478,10 |
| 7 | 27 | -3,82 | 212,94 |
| 8 | 22 | -8,82 | 6051,66 |
| 9 | 18 | -12,82 | 27011,71 |
| 10 | 38 | 7,18 | 2657,65 |
| 11 | 42 | 11,18 | 15623,10 |
| 12 | 39 | 8,18 | 4477,27 |
| 13 | 32 | 1,18 | 1,94 |
| 14 | 45 | 14,18 | 40430,11 |
| 15 | 39 | 8,18 | 4477,27 |
| 16 | 44 | 13,18 | 30176,00 |
| 17 | 15 | -15,82 | 62636,27 |
| 18 | 47 | 16,18 | 68535,26 |
| 19 | 36 | 5,18 | 719,98 |
| 20 | 35 | 4,18 | 305,28 |
| 21 | 28 | -2,82 | 63,24 |
| 22 | 16 | -14,82 | 48238,39 |
| 23 | 26 | -4,82 | 539,74 |
| 24 | 38 | 7,18 | 2657,65 |
| 25 | 42 | 11,18 | 15623,10 |
| 26 | 30 | -0,82 | 0,45 |
| 27 | 13 | -17,82 | 100839,50 |
| 28 | 43 | 12,18 | 22008,43 |
| 29 | 36 | 5,18 | 719,98 |
| 30 | 21 | -9,82 | 9299,21 |
| 31 | 40 | 9,18 | 7101,84 |
| 32 | 48 | 17,18 | 87114,94 |
| 33 | 36 | 5,18 | 719,98 |
| 34 | 18 | -12,82 | 27011,71 |
| 35 | 40 | 9,18 | 7101,837 |
| 36 | 43 | 12,18 | 22008,43 |
| 37 | 17 | -13,82 | 36478,10 |
| 38 | 27 | -3,82 | 212,94 |
| 39 | 15 | -15,82 | 62636,27 |
| 40 | 19 | -11,82 | 19519,55 |
| 41 | 29 | -1,82 | 10,97 |
| 42 | 26 | -4,82 | 539,74 |
| 43 | 34 | 3,18 | 102,26 |
| 44 | 32 | 1,18 | 1,94 |
| 45 | 19 | -11,82 | 19519,55 |
| 46 | 16 | -14,82 | 48238,39 |
| 47 | 25 | -5,82 | 1147,34 |
| 48 | 17 | -13,82 | 36478,10 |
| 49 | 18 | -12,82 | 27011,71 |
| 50 | 39 | 8,18 | 4477,27 |
| ∑ | 1670983,16 |
Е=![]() =
=![]()
![]() =-0,29
=-0,29
Таким образом, эксцесс полученного нами эмпирического распределения равен -0,29
Тот факт, что А и Е не равны 0 говорит об аномальности оцениваемого распределения. Однако, мы видим, что эти значения очень близки к нулю. И все же нормальный закон распределения не подтвердился, и говорит о необходимости пересмотра части репрезентативности выборки, либо части теста.
ЗАКЛЮЧЕНИЕ
Итак, мы разработали тест-опросник, предназначенный для диагностики уровня тревожности у студентов последних курсов. Мы определили надежность, валидность теста, выявили вопросы, которые необходимо исключить из теста. Произведенные расчеты позволяют сделать вывод, о том, что созданный и проверенный опросник соответствует требованиям к тестам.
Проведенное исследование позволило скомпоновать блоки вопросов, которые могут рассматриваться как средство для анализа уровня тревожности.
Конечно, разработку данного опросника нельзя признать завершенной - для его стандартизации требуются значительно большие выборки, - но что касается его структуры, то она представляется достаточно оптимальной.
В заключении надо сказать, что этот опросник может быть использован прежде всего там, где есть возможность - либо в индивидуальной консультации, либо в групповой тренинговой работе - соотносить те или иные методические (коррекционные) средства с индивидуальными особенностями испытуемого.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Абрамова Г.С. Практическая психология. Изд. 3 Екатеринбург: “Деловая книга”, 1998.
2. Барлас Т.В. Психодиагностика в психологическом консультировании: задачи и подходы // Журнал практической психологии и психоанализа, №1, 2003
3. Гайда В.К., Захаров В.П. Психологическое тестирование: учебное пособие. – Л. : Изд-во ЛГУ, 1982.
4. Клайн П. Справочное руководство по конструированию тестов. Киев, 1994
5. Немов Р. С. Психология: В 3 кн. Кн. 3: Психодиагностика. М.: “ВЛАДОС”, 1998.
6. Немов Р.С. Психология. Учебник для студентов высш, учеб, заведений. В 3 кн. Кн. 1. Общие основы психологии. 2-е изд. М., 1995.
7. Словарь-справочник по психологической диагностике / Бурлачук Л.Ф., Морозов С.М., отв. ред. С.Б. Крымский. – Киев: Наук. думка, 1989.
ПРИЛОЖЕНИЕ 1
Личностная шкала проявлений тревоги Дж. Тейлора
Опросник состоит из 60 утверждений. Предъявляется испытуемому как набор карточек с утверждениями.
Вам предлагается ознакомиться с набором высказываний, касающихся черт характера. Если вы согласны с утверждением, отвечайте «Да», если не согласны - «Нет». Долго не задумывайтесь, важен первый пришедший вам в голову ответ.
1. Обычно я спокоен и вывести меня из себя нелегко.
2. Мои нервы расстроены не больше, чем у других людей.
3. У меня редко бывают запоры.
4. У меня редко бывают головные боли.
5. Я редко устаю.
6. Я почти всегда чувствую себя вполне счастливым.
7. Я уверен в себе.
8. Практически я никогда не краснею.
9. По сравнению со своими друзьями я считаю себя вполне смелым человеком.
10. Я краснею не чаще, чем другие.
11. У меня редко бывает сердцебиение.
12. Обычно мои руки достаточно теплые.
13. Я застенчив не более, чем другие.
14. Мне не хватает уверенности в себе.
15. Порой мне кажется, что я ни на что не годен.
16. У меня бывают периоды такого беспокойства, что я не могу усидеть на месте.
17. Мой желудок сильно беспокоит меня.
18. У меня не хватает духа вынести все предстоящие трудности.
19. Я хотел бы быть таким же счастливым, как другие.
20. Мне кажется порой, что передо мной нагромождены такие трудности, которые мне не преодолеть.
21. Мне нередко снятся кошмарные сны.
22. Я замечаю, что мои руки начинают дрожать, когда я пытаюсь что-либо сделать.
23. У меня чрезвычайно беспокойный и прерывистый сон.
24. Меня весьма тревожат возможные неудачи.
25. Мне приходилось испытывать страх в тех случаях, когда я точно знал, что мне ничто не угрожает.
26. Мне трудно сосредоточиться на работе или на каком-либо задании.
27. Я работаю с большим напряжением.
28. Я легко прихожу в замешательство.
29. Почти все время я испытываю тревогу из-за кого-либо или из-за чего-либо.
30. Я склонен принимать все слишком серьезно.
31. Я часто плачу.
32. Меня нередко мучают приступы рвоты и тошноты.
33. Раз в месяц или чаще у меня бывает расстройство желудка.
34. Я часто боюсь, что вот-вот покраснею.
35. Мне очень трудно сосредоточиться на чем-либо.
36. Мое материальное положение весьма беспокоит меня.
37. Нередко я думаю о таких вещах, о которых ни с кем не хотелось бы говорить.
38. Я часто испытываю чувство вины.
39. У меня бывали периоды, когда тревога лишала меня сна.
40. Временами, когда я нахожусь в замешательстве, у меня появляется сильная потливость, что очень смущает меня.
41. Даже в холодные дни я легко потею.
42. Временами я становлюсь таким возбужденным, что мне трудно заснуть.
43. Я человек легко возбудимый.
44. Временами я чувствую себя совершенно бесполезным.
45. Порой мне кажется, что мои нервы сильно расшатаны и я вот-вот выйду из себя.
46. Я часто ловлю себя на том, что меня что-то тревожит.
47. Я гораздо чувствительнее, чем большинство других людей.
48. Я почти все время испытываю чувство голода.
49. Ожидание меня нервирует.
50. Жизнь для меня связана с необычным напряжением.
51. Меня нередко охватывает отчаяние.
52. У меня нет прежней энергичности, я стал более медлительным и вялым.
53. Я люблю быть один.
54. Меня легко переубедить.
55. Я часто жалею о своих поступках.
56. Прошлое лучше настоящего.
57. Моя работа, требует значительной сосредоточенности и внимания.
58. Я нахожусь в постоянном напряжении.
59. Мне тяжело принимать решения из-за постоянных сомнений.
60. Я сам виноват во всех своих неприятностях.
ПРИЛОЖЕНИЕ 2
Шкала социальной желательности
(Шкала лжи)
1. Я внимательно читаю каждую книгу, прежде чем вернуть ее в библиотеку
2. Я не испытываю колебаний, когда кому-нибудь нужно помочь в беде.
3. Я всегда внимательно слежу за тем, как я одет.
4. Дома я веду себя за столом так же, как в столовой.
5. Я никогда ни к кому не испытывал антипатии.
6. Был случай, когда я бросил что-то делать, потому что не был уверен в своих силах.
7. Иногда я люблю позлословить об отсутствующих.
8. Я всегда внимательно слушаю собеседника, кто бы он ни был.
9. Был случай, когда я придумал вескую причину, чтобы оправдаться.
10. Случалось, я пользовался оплошностью человека.
11. Я всегда охотно признаю свои ошибки.
12. Я азартный человек.
13. Иногда вместо того, чтобы простить человека, я стараюсь отплатить ему тем же.
14. Были случаи, когда я настаивал на том, чтобы делали по-моему.
15. У меня не возникает внутреннего протеста, когда меня просят оказать услугу.
16. У меня никогда не возникает досады, когда высказывают мнение, противоположное моему.
17. Перед длительной поездкой я всегда тщательно продумываю, что взять с собой.
18. Были случаи, когда я завидовал удаче других.
19. Иногда меня раздражают люди, которые обращаются ко мне с вопросами.
20. Когда у людей неприятности, я иногда думаю, что они получили по заслугам.
21. Я никогда с улыбкой не говорил неприятных вещей.
22. В игре я предпочитаю выигрывать.
23. Если мне не грозит штраф, то я перехожу улицу там, где удобно, а не там, где положено.
24. Не мои знакомые мне нравятся.
ПРИЛОЖЕНИЕ 3
Опросник для диагностики уровня тревоги у студентов
последних курсов
Уважаемый испытуемый! Мы исследуем человеческие страхи. Многие люди хоть раз в жизни чувствовали тревогу перед будущим. Страхи есть у всех и стыдиться их нечего. Но с ними нужно бороться, а для этого нужно знать о них побольше. Понять какие меры возможно принять для устранения страха перед будущим может помочь ваше мнение. Опрос анонимный, поэтому вы можете быть полностью откровенны. Прочитайте внимательно инструкцию, и отвечайте в соответствии с нею.
Инструкция: в этом блоке просто поставьте крестик в той клетке, номер которой совпадает с Вашим мнением.
| вопросы | да | нет |
|
1. Вы всегда держите свои обещания, даже если вам это не нравится? 2. У Вас бывают холодные руки, если Вы находитесь в теплом помещении? 3. У вас часто болит голова? 4. Вы уверены в своих силах? 5. Вы нервничаете, если приходится кого-то долго ждать? 6. Были ли у вас минуты, когда Вам казалось, что Вы хуже всех? 7. Вы счастливы? 8. Вы были послушным ребенком? 9. Расстройство желудка – обычное для Вас явление? 10. Вы часто испытываете беспричинную тревогу? 11. Вы застенчивы? 12. Бывает ли, что вы говорите о чем-то, в чем мало разбираетесь? 13. Часто ли Вы краснеете? 14. Вы обращаете внимание на пустяки? 15. У вас бывает одышка? 16. Друзья Ваших друзей всегда нравятся Вам?? 17. Бывало ли, что из-за тревог Вы не могли уснуть? 18. Вас легко расстроить? 19. Вам снятся кошмары? 20. Вам говорили, что Вы все принимаете слишком серьезно? 21. Вы потеете, когда нервничаете? 22. Вы спите спокойно ночью? 23. Вы не терпите поражений в играх? 24. Считаете ли Вы себя чувствительным человеком? 25. У вас хорошее чувство юмора? 26. Ваша жизнь складывается лучше, чем у других? 27. У вас есть проблемы с желудочно-кишечным трактом? 28. У вас есть материальные проблемы? 29. Вы доверяете людям? 30. Вы легко преодолеваете трудности? 31. Вас легко смутить? 32. Часто ли Вы попадаете в конфликтные ситуации? 33. Вы часто испытываете приступы тошноты и рвоты? 34. Вас можно назвать пунктуальным человеком? 35. Случалось ли Вам чувствовать себя бесполезным? 36. Вы используете нецензурные выражения? 37. Вы испытываете тревогу по любому поводу? 38. Вы боитесь неудач? 39. Вы стараетесь не показывать своих эмоций на публике? 40. Вам приходилось испытывать отчаяние? 41. Вас легко «завести»? 42. У вас дрожат руки, когда Вы волнуетесь? 43. Вы часто в течение дня испытываете чувство голода? 44. Вы потеете в прохладные дни? 45. Вы рассказывали о своих мечтах кому-нибудь? 46. Вас часто беспокоят боли в животе? 47. После прочтения полученного письма Вы всегда сразу пишите ответ? 48. У вас меньше опасений и страхов, чем у ваших знакомых? 49. Бывает ли, что Вы откладываете на завтра то, что можно сделать сегодня? 50. Ваша учеба требует от Вас большого напряжения? |
ПРИЛОЖЕНИЕ 4
Ключ к опроснику
| вопросы | да | нет |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
+ + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + + |
+ + + + + + + + + + + + + + + + + + |
| Номер испытуемого | Балл за ответ | ПРИЛОЖЕНИЕ5 |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
хi | bi | х1i | х2i | yi | |||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 46 | 45 | 24 | td>244 | |||||||
| 2 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 43 | 43 | 24 | 19 | 42 | ||||||
| 3 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 40 | 41 | 19 | 21 | 42 | ||||||
| 4 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 30 | 34 | 14 | 16 | 36 | ||||||
| 5 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 35 | 35 | 19 | 16 | 40 | ||||||
| 6 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 17 | 23 | 7 | 10 | 36 | ||||||
| 7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 27 | 26 | 14 | 13 | 32 | ||||||
| 8 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 22 | 29 | 13 | 9 | 32 | ||||||
| 9 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 18 | 21 | 10 | 8 | 27 | ||||||
| 10 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 38 | 38 | 18 | 20 | 44 | ||||||
| 11 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 42 | 42 | 22 | 20 | 47 | ||||||
| 12 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 39 | 40 | 18 | 21 | 39 | ||||||
| 13 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 32 | 34 | 17 | 15 | 35 | ||||||
| 14 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 45 | 44 | 23 | 22 | 46 | ||||||
| 15 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 39 | 40 | 20 | 19 | 42 | ||||||
| 16 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 44 | 45 | 22 | 22 | 42 | ||||||
| 17 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 15 | 18 | 9 | 6 | 29 | ||||||
| 18 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 47 | 47 | 24 | 23 | 49 | ||||||
| 19 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 36 | 38 | 19 | 17 | 42 | ||||||
| 20 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 35 | 35 | 21 | 14 | 36 | ||||||
| 21 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 28 | 28 | 14 | 14 | 32 | ||||||
| 22 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 16 | 20 | 8 | 8 | 28 | ||||||
| 23 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 26 | 26 | 11 | 15 | 28 | ||||||
| 24 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 38 | 38 | 19 | 19 | 38 | ||||||
| 25 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 42 | 43 | 22 | 20 | 44 | ||||||
| 26 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 30 | 32 | 16 | 14 | 35 | ||||||
| 27 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 13 | 16 | 7 | 6 | 18 | ||||||
| 28 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 43 | 42 | 22 | 21 | 42 | ||||||
| 29 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 36 | 38 | 19 | 17 | 40 | ||||||
| 30 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 21 | 24 | 10 | 11 | 26 | ||||||
| 31 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 40 | 40 | 18 | 22 | 38 | ||||||
| 32 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 48 | 47 | 25 | 23 | 45 | ||||||
| 33 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 36 | 37 | 17 | 19 | 40 | ||||||
| 34 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 18 | 20 | 10 | 8 | 26 | ||||||
| 35 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 40 | 40 | 20 | 20 | 44 | ||||||
| 36 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 43 | 44 | 22 | 21 | 42 | ||||||
| 37 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 17 | 19 | 9 | 8 | 23 | ||||||
| 38 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 27 | 29 | 12 | 15 | 33 | ||||||
| 39 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 15 | 18 | 7 | 8 | 25 | ||||||
| 40 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 19 | 19 | 11 | 8 | 28 | ||||||
| 41 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 29 | 29 | 15 | 14 | 30 | ||||||
| 42 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 26 | 28 | 15 | 11 | 31 | ||||||
| 43 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 34 | 35 | 18 | 16 | 33 | ||||||
| 44 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 32 | 33 | 17 | 15 | 35 | ||||||
| 45 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 19 | 19 | 11 | 8 | 24 | ||||||
| 46 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 16 | 17 | 8 | 8 | 18 | ||||||
| 47 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 25 | 25 | 11 | 14 | 26 | ||||||
| 48 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 17 | 18 | 7 | 10 | 24 | ||||||
| 49 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 18 | 18 | 11 | 7 | 18 | ||||||
| 50 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 39 | 39 | 18 | 21 | 36 | ||||||
| 41 | 16 | 23 | 32 | 37 | 46 | 35 | 45 | 38 | 14 | 27 | 13 | 29 | 42 | 33 | 23 | 39 | 9 | 36 | 25 | 34 | 34 | 27 | 35 | 25 | 47 | 36 | 40 | 32 | 26 | 34 | 42 | 37 | 26 | 42 | 24 | 13 | 11 | 26 | 40 | 30 | 33 | 21 | 34 | 33 | 33 | 35 | 31 | 24 | 33 | 1541 | |||||