Реферат: Сводка статистических данных

Реферат

Статистика

Сводка статистических данных

Москва 2005г.

Содержание

Сводка статистических данных

Ошибки выборки

Список литературы

Сводка статистических данных

В результате первой стадии статистического исследования (статистического наблюдения) получают статистическую информацию, представляющую собой большое количество первичных, разрозненных сведений об отдельных единицах объекта исследо­вания (записи о каждом гражданине страны при переписи насе­ления: пол, национальность, возраст, образование, род занятий и многие другие признаки). Дальнейшая задача статистики заклю­чается в том, чтобы привести эти материалы в определенный по­рядок, систематизировать и на этой основе дать сводную характе­ристику всей совокупности фактов при помощи обобщающих статистических показателей, отражающих сущность социально-экономических явлений и определенные статистические законо­мерности. Это достигается в результате сводки — второй стадии статистического исследования.

Статистическая сводка — это научно организованная обработка материалов наблюдения, включающая в себя систематиза­цию, группировку данных, составление таблиц, подсчет групповых и общих итогов, расчет производных показателей (средних, относительных величин). Она позволяет перейти к обобщаю­щим показателям совокупности в целом и отдельных ее частей, осуществлять анализ и прогнозирование изучаемых процессов.

Если производится только подсчет общих итогов по изучае­мой совокупности единиц наблюдения, то сводка называется простой. Например, для получения общей численности студентов высших учебных заведений России достаточно сложить данные о численности студентов всех высших учебных заведе­ний (на конец 1998 г. — 3,6 млн. чел.).

По технике или способу выполнения сводка может быть руч­ной либо механизированной (с помощью ЭВМ).

Статистическая сводка проводится по определенной про­грамме и плану.

Программа статистической сводки устанавливает следую­щие этапы:

• выбор группировочных признаков;

• определение порядка формирования групп;

• разработка системы статистических показателей для ха­рактеристики групп и объекта в целом;

• разработка макетов статистических таблиц для представления результатов сводки.

План статистической сводки содержит указания о последовательности и сроках выполнения отдельных частей сводки, ее ис­полнителях и о порядке изложения и представления результатов.

В сводке статистического материала отдельные единицы ста­тистической совокупности объединяются в группы при помощи метода группировок.

Статистическая группировка — это процесс образования однородных групп на основе расчленения статистической сово­купности на части или объединения изучаемых единиц в част­ные совокупности по существенным для них признакам, каждая из которых характеризуется системой статистических показате­лей. Например, группировка промышленных предприятий по формам собственности, группировка населения по размеру среднедушевого дохода, группировка коммерческих банков по сумме активов баланса и т.д.

Особым видом группировок является классификация, представ­ляющая собой устойчивую номенклатуру классов и групп, обра­зованных на основе сходства и различия единиц изучаемого объ­екта. Классификация выступает в роли своеобразного статистиче­ского стандарта, устанавливаемого на определенный промежуток времени, например, ЕГРПО. Общероссийский классификатор видов экономической деятельности, продукции и услуг (ОКПД), классификация основных фондов в промышленности, строительстве, капитальных вложений, затрат на производство и т.д.

Метод статистических группировок позволяет разрабатывать первичный статистический материал. На основе группировки рассчитываются сводные показатели по группам, появляется возмож­ность их сравнения, анализа причин различий между группами, изучения взаимосвязей между признаками. Расчет сводных показа­телей в целом по совокупности позволяет изучить ее структуру.

Кроме того, группировка создает основу для последующей сводки и анализа данных. Этим определяется роль группировок как научной основы сводки.

Большие достижения в области применения метода группи­ровок имеет современная отечественная статистика. Введение группировочных таблиц, содержащих показатели международ­ной системы национальных счетов (СНС), превращает группировки (классификации) в эффективный метод анализа и вскры­тия резервов в экономике.

Ошибки выборки

При выборочном наблюдении должна быть обеспечена слу­чайность отбора единиц. Каждая единица должна иметь равную с другими возможность быть отобранной. Именно на этом основывается собственно-случайная выборка.

К собственно-случайной выборке относится отбор единиц из всей генеральной совокупности (без предварительного рас­членения ее на какие-либо группы) посредством жеребьевки (преимущественно) или какого-либо иного подобного спосо­ба, например, с помощью таблицы случайных чисел. Случай­ный отбор — это отбор не беспорядочный. Принцип случай­ности предполагает, что на включение или исключение объ­екта из выборки не может повлиять какой-либо фактор, кро­ме случая. Примером собственно-случайного отбора могут служить тиражи выигрышей: из общего количества выпущен­ных билетов наугад отбирается определенная часть номеров, на которые приходятся выигрыши. Причем всем номерам обеспечивается равная возможность попадания в выборку. При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки.

Доля выборки есть отношение числа единиц выборочной со­вокупности к числу единиц генеральной совокупности:

Так, при 5%-ной выборке из партии деталей в 1000 ед. объ­ём выборки п составляет 50 ед., а при 10%-ной выборке — 100 ед. и т.д. При правильной научной организации выборки ошибки репрезентативности можно свести к минимальным значениям, в результате — выборочное наблюдение становится достаточно точным.

Собственно-случайный отбор «в чистом виде» применяет­ся в практике выборочного наблюдения редко, но он является исходным среди всех других видов отбора, в нем заключаются и реализуются основные принципы выборочного наблюдения.

Рассмотрим некоторые вопросы теории выборочного метода и формулы ошибок для простой случайной выборки.

Применяя выборочный метод в статистике, обычно используют два основных вида обобщающих показателей: среднюю величину ко­личественного признака и относительную величину альтернативного признака (долю или удельный вес единиц в статистической совокупности, которые отличаются от всех других единиц этой сово­купности только наличием изучаемого признака).

Выборочная доля (w), или частость, определяется отношением числа единиц, обладающих изучаемым признаком т, к общему числу единиц выборочной совокупности п:

w=m/n.

Например, если из 100 деталей выборки (n =100), 95 деталей оказались стандартными (т =95), то выборочная доля

w=95/100=0,95 .

Для характеристики надежности выборочных показателей различают среднюю и предельную ошибки выборки.

Ошибка выборки ε или, иначе говоря, ошибка репрезента­тивности представляет собой разность соответствующих выбо­рочных и генеральных характеристик:

•        для средней количественного признака

;     (форм. 1)

•        для доли (альтернативного признака)

;     (форм. 2)

Ошибка выборки свойственна только выборочным наблюде­ниям. Чем больше значение этой ошибки, тем в большей степе­ни выборочные показатели отличаются от соответствующих генеральных показателей.

Выборочная средняя и выборочная доля по своей сути яв­ляются случайными величинами, которые могут принимать раз­личные значения в зависимости от того, какие единицы сово­купности попали в выборку. Следовательно, ошибки выборки также являются случайными величинами и могут принимать различные значения. Поэтому определяют среднюю из возмож­ных ошибок — среднюю ошибку выборки.

От чего зависит средняя ошибка выборки? При соблюдении принципа случайного отбора средняя ошибка выборки определя­ется прежде всего объемом выборки: чем больше численность при прочих равных условиях, тем меньше величина средней ошибки выборки. Охватывая выборочным обследованием все большее количество единиц генеральной совокупности, всё более точно характеризуем всю генеральную совокупность.

Средняя ошибка выборки также зависит от степени варьи­рования изучаемого признака. Степень варьирования, как из­вестно, характеризуется дисперсией σ² или w(1-w) — для альтернативного признака. Чем меньше вариация признака, а следовательно, и дисперсия, тем меньше средняя ошибка вы­борки, и наоборот. При нулевой дисперсии (признак не варь­ирует) средняя ошибка выборки равна нулю, т. е. любая еди­ница генеральной совокупности будет совершенно точно ха­рактеризовать всю совокупность по этому признаку.

Зависимость средней ошибки выборки от ее объема и степе­ни варьирования признака отражена в формулах, с помощью которых можно рассчитать среднюю ошибку выборки в условиях выборочного наблюдения, когда генеральные характеристики (х ,p) неизвестны, и следовательно, не представляется возмож­ным нахождение реальной ошибки выборки непосредственно по формулам (форм. 1), (форм. 2).

Ø  При случайном повторном отборе средние ошибки теоретически рассчитывают по следующим формулам:

•        для средней количественного признака

;     (форм. 3)

•        для доли (альтернативного признака)

;     (форм. 4)

Поскольку практически дисперсия признака в генеральной совокупности σ² точно неизвестна,  на практике пользуются значением дисперсии S², рассчитанным для выборочной сово­купности на основании закона больших чисел, согласно кото­рому выборочная совокупность при достаточно большом объеме выборки достаточно точно воспроизводит характеристики гене­ральной совокупности.

Таким образом, расчетные формулы средней ошиб­ки выборки при случайном повторном отборе будут следующие:

•        для средней количественного признака

;     (форм. 5)

•        для доли (альтернативного признака)

.     (форм. 6)

Однако дисперсия выборочной совокупности не равна диспер­сии генеральной совокупности, и следовательно, средние ошибки выборки, рассчитанные по формулам (форм. 5) и (форм. 6), будут прибли­женными. Но в теории вероятностей доказано, что генеральная дисперсия выражается через выборную следующим соотношением:

.     (форм. 7)

Так как п/(n -1) при достаточно больших п — величина, близкая к единице, то можно принять, что , а следова­тельно, в практических расчетах средних ошибок выборки мож­но использовать формулы (форм. 5) и (форм. 6). И только в случаях ма­лой выборки (когда объем выборки не превышает 30) необхо­димо учитывать коэффициент п/(n-1) и исчислять среднюю ошибку малой выборки по формуле:

.     (форм. 8)

Ø  X При случайном бесповторном отборе в приведенные выше формулы расчета средних ошибок выборки необходимо подко­ренное выражение умножить на 1-(n/N), поскольку в процес­се бесповторной выборки сокращается численность единиц генеральной совокупности. Следовательно, для бесповторной вы­борки расчетные формулы средней ошибки выборки примут такой вид:

•        для средней количественного признака

;     (форм. 9)

• для доли (альтернативного признака)

.     (форм. 10)

Так как п всегда меньше N, то дополнительный множи­тель 1-(n/N) всегда будет меньше единицы. Отсюда следу­ет, что средняя ошибка при бесповторном отборе всегда будет меньше, чем при повторном. В то же время при сравнительно небольшом проценте выборки этот множитель близок к еди­нице (например, при 5%-ной выборке он равен 0,95; при 2%-ной — 0,98 и т.д.). Поэтому иногда на практике пользуются для определения средней ошибки выборки формулами (форм. 5) и (форм. 6) без указанного множителя, хотя выборку и организуют как бесповторную. Это имеет место в тех случаях, когда число единиц генеральной совокупности N неизвестно или безгра­нично, или когда п очень мало по сравнению с N, и по су­ществу, введение дополнительного множителя, близкого по значению к единице, практически не повлияет на значение средней ошибки выборки.

Механическая выборка состоит в том, что отбор единиц в выборочную совокупность из генеральной, разбитой по ней­тральному признаку на равные интервалы (группы), произво­дится таким образом, что из каждой такой группы в выборку отбирается лишь одна единица. Чтобы избежать систематиче­ской ошибки, отбираться должна единица, которая находится в середине каждой группы.

При организации механического отбора единицы совокуп­ности предварительно располагают (обычно в списке) в опре­деленном порядке (например, по алфавиту, местоположению, в порядке возрастания или убывания значений какого-либо по­казателя, не связанного с изучаемым свойством, и т.д.), после чего отбирают заданное число единиц механически, через оп­ределенный интервал. При этом размер интервала в генеральной совокупности равен обратному значению доли выборки. Так, при 2%-ной выборке отбирается и проверяется каждая 50-я единица (1 : 0,02), при 5%-ной выборке — каждая 20-я едини­ца (1 : 0,05), например, сходящая со станка деталь.

При достаточно большой совокупности механический отбор по точности результатов близок к собственно-случайному. По­этому для определения средней ошибки механической выборки используют формулы собственно-случайной бесповторной вы­борки (форм. 9), (форм. 10).

Для отбора единиц из неоднородной совокупности применя­ется, так называемая типическая выборка, которая используется в тех случаях, когда все единицы генеральной совокупности можно разбить на несколько качественно однородных, однотипных групп по признакам, влияющим на изучаемые показатели.

При обследовании предприятий такими группами могут быть, например, отрасль и подотрасль, формы собственности. Затем из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность.

Типическая выборка обычно применяется при изучении слож­ных статистических совокупностей. Например, при выборочном обследовании семейных бюджетов рабочих и служащих в отдель­ных отраслях экономики, производительности труда рабочих пред­приятия, представленных отдельными группами по квалификации.

Типическая выборка дает более точные результаты по сравнению с другими способами отбора единиц в выбороч­ную совокупность. Типизация генеральной совокупности обеспечивает репрезентативность такой выборки, представи­тельство в ней каждой типологической группы, что позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки.

При определении средней ошибки типической выборки в ка­честве показателя вариации выступает средняя из внутригрупповых дисперсий.

Среднюю ошибку выборки находят по формулам:

•        для средней количественного признака

(повторный отбор);     (форм. 11)

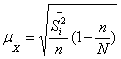(бесповоротный отбор);     (форм. 12)

•        для доли (альтернативного признака)

(повторный отбор);     (форм.13)

(бесповторный отбор),     (форм. 14)

где - средняя из внутригрупповых дисперсий по вы­борочной совокупности;

- средняя из внутригрупповых дисперсий доли (альтернативного признака) по выборочной совокупности.

Серийная выборка предполагает случайный отбор из генераль­ной совокупности не отдельных единиц, а их равновеликих групп (гнезд, серий) с тем, чтобы в таких группах подвергать наблюде­нию все без исключения единицы.

Применение серийной выборки обусловлено тем, что многие товары для их транспортировки, хранения и продажи упаковываются в пачки, ящики и т.п. Поэтому при контроле качества упакованного товара рациональнее проверить не­сколько упаковок (серий), чем из всех упаковок отбирать необходимое количество товара.

Поскольку внутри групп (серий) обследуются все без исключе­ния единицы, средняя ошибка выборки (при отборе равновеликих серий) зависит только от межгрупповой (межсерийной) дисперсии.

Ø  Среднюю ошибку выборки для средней количественного признака при серийном отборе находят по формулам:

(повторный отбор);     (форм.15)

(бесповторный отбор),     (форм. 16)

где r - число отобранных серий; R - общее число серий.

Межгрупповую дисперсию серийной выборки вычисляют сле­дующим образом:

,

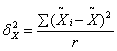где  - средняя i - й серии;  - общая средняя по всей выбо­рочной совокупности.

Ø  Средняя ошибка выборки для доли (альтернативного при­знака) при серийном отборе:

(повторный отбор);     (форм. 17)

(бесповторный отбор).     (форм. 18)

Межгрупповую (межсерийную) дисперсию доли серийной вы­борки определяют по формуле:

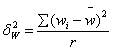,     (форм. 19)

где  - доля признака в i-й серии; - общая доля признака во всей выборочной совокупности.

В практике статистических обследований помимо рассмот­ренных ранее способов отбора применяется их комбинация (комбинированный отбор).

Список литературы

Гусаров В.М. Теория статистики: уч. М.: ЮНИТИ, Аудит, 1998

Колбачёв Е.Б. Основы статистики. Учебник. М.: Ростов-на-Дону, Феникс,1999