Контрольная работа: Общая теория статистики
Задача № 1
Для изучения производительности труда рабочих завода было проведено 10% -ое выборочное обследование по методу случайного бесповторного отбора, в результате которого получены следующие данные о дневной выработке изделий рабочими:
Дневная выработка рабочих.
Таблица 1
| Количество изделий за смену, шт. | Число рабочих |
| До 20 | 5 |
| 20-22 | 15 |
| 22-24 | 35 |
| 24-26 | 80 |
| 26-28 | 95 |
| 28-30 | 4 |
| Свыше 30 | 1 |
На основании этих данных вычислите:
1. среднюю сменную выработку;
2. моду и медиану;
3. размах вариаций;
4. среднее линейное отклонение;
5. дисперсию;
6. среднее квадратичное отклонение;
7. коэффициент вариации, оцените однородность совокупности;
8. с вероятностью 0,954 предельную ошибку выборки и возможные границы, в которых можно ожидать среднюю выработку рабочих завода;
9. с той же вероятностью пределы удельного веса числа рабочих, вырабатывающих за смену свыше 26 изделий.
Сделайте выводы.
Решение:
За величины открытых интервалов (у которых верхняя или нижняя границы точно не определены) условно примем величины смежного закрытого интервала. Т.е. величина интервала первого интервала равна величине второго интервала и равна 2, а величина 7-го интервала равна величине 6-го и равна 2. Найдем среднее значение признака по формуле:
![]() ,
,
где ![]() -
среднее значение признака; xi - значение признака на интервале (середина
интервала); mi - частота повторения признака на интервале.
-
среднее значение признака; xi - значение признака на интервале (середина
интервала); mi - частота повторения признака на интервале.
![]() .
.
Найдем моду и медиану выборки. Мода - это наиболее часто повторяющееся значение признака. Для данной выборки мода равна группе 26-28. Медиана - величина признака, которая делит упорядоченную последовательность его значений на две равные по численности части. Для данной выборки медианный интервал равен 24-26. Таким образом, чаще всего, изготавливают от 24 до 26 деталей, причем половина рабочих изготавливает больше 25 деталей. Найдем размах вариаций. Нижняя граница выборки равна xmin= 18; верхняя граница выборки равна xmax= 30 + 2 = 32.
Размах вариаций H = xmax - xmin = 32 - 18 = 14.
Среднее линейное отклонение найдем по формуле:
 ,
,
где Л - среднее линейное отклонение.
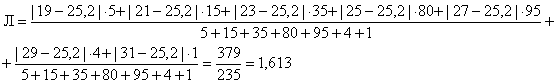
Найдем дисперсию признака по формуле:
![]() ,
,
где ![]() -
дисперсия признака.
-
дисперсия признака.
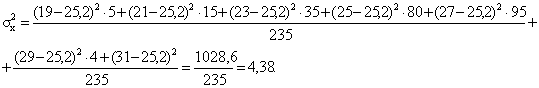
Среднее квадратичное отношение ![]() .
.
Коэффициент вариации ![]() .
.
Коэффициент вариации меньше 33 %, значит выборка однородная.
Возможные пределы, в которых ожидается средняя выработка рабочих завода с вероятностью 0,954 найдем из формулы:
![]()
где t - коэффициент доверия при заданной степени вероятности (находится по таблице).
![]() -
средняя ошибка выборочной средней;
-
средняя ошибка выборочной средней;
![]() -
предельная ошибка выборки Δ.
-
предельная ошибка выборки Δ.
Средняя ошибка выборочной средней находится по формуле:
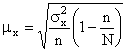 ,
,
где N - общее число изделий.
В нашем случае n / N = 0,1, т.к проводилось обследование 10% изделий.
![]() .
.
t (0,954; 100) = 2,0, следовательно предельная ошибка и интервал равны:
Δ = 2,0 · 0,13 = 0,26 шт.
(25,2 - 0,26; 25,2 + 0,26) (24,94; 25,46).
Т. е. средняя выработка рабочих завода с вероятностью 0,954 будет в интервале от 24,94 до 25,46 штук за смену.
Возможные пределы удельного веса числа рабочих, вырабатывающих более 26 изделий за смену с вероятностью 0,954 найдем из формулы:
![]() ,
,
где![]() -
средняя ошибка выборочной доли. Она находится по формуле:
-
средняя ошибка выборочной доли. Она находится по формуле:
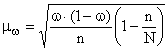 ,
,
![]() -
частота появления альтернативного признака, равная m/n, где m - число случаев в
выборке, когда стаж попадает в заданный интервал. В нашем случае m = 95 + 4 + 1
= = 100 и
-
частота появления альтернативного признака, равная m/n, где m - число случаев в
выборке, когда стаж попадает в заданный интервал. В нашем случае m = 95 + 4 + 1
= = 100 и ![]() = 100/235 = 0,43. Тогда:
= 100/235 = 0,43. Тогда:
![]() ,
,
t (0,954) = 2,0, предельная
ошибка выборочной доли равна ![]() = 0,06
= 0,06
Следовательно интервал равен:
(0,43 - 0,06; 0,43 + 0,06); (0,424; 0,436).
Т. е. с вероятностью 0,954 от 42,4% до 43,6% рабочих будет вырабатывать более 26 изделий за смену.
Задача №2.
Имеются следующие данные о продаже товаров на колхозном рынке города.
Таблица 2. Реализация товаров на рынке города
| Наименование товара | Средняя цена единицы товара, руб. | Продано товара, тыс. ед. | ||
| Базис | Отчет | Базис | Отчет | |
| Молоко, л | 3500 | 3000 | 500 | 500 |
| Картофель, кг | 1500 | 1000 | 600 | 700 |
| Морковь, кг | 3000 | 2000 | 150 | 200 |
Определите:
1. индивидуальные индексы цен и количества проданных товаров;
2. общий индекс цен;
3. общий индекс физического объема товарооборота;
4. выполните факторный анализ.
На основании индексов, исчисленных в пунктах 2,3, используя взаимосвязь индексов определить, на сколько процентов изменился товарооборот в фактических ценах.
Решение:
Индивидуальный индекс цены найдем по формуле:
![]() ,
,
гдеip - индивидуальный индекс цены продукции,
p1 и p0 - цена продукции в отчетном и базисном периодах соответственно.
Найдем индивидуальные индексы цен для всех товаров
[молоко] ip = 3000/3500 = 0,857.
[картофель] ip = 1000/1500 = 0,667.
[морковь] ip = 2000/3000 = 0,667.
Индивидуальный индекс объема продукции найдем по формуле:
![]() ,
,
гдеiq - индивидуальный индекс объема продукции,
q1 и q0 - объем продукции в отчетном и базисном периодах соответственно. Найдем индивидуальные индексы физического объема для всех товаров:
[молоко] iq = 500/500 = 1,0., [картофель] iq = 700/600 = 1,667.
[морковь] iq = 200/150 = 1,333.
Общий индекс цен найдем по формуле:
![]() ,
,
где Ip - общий индекс цен.
![]() .
.
Общий индекс физического объема найдем по формуле:
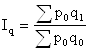 ,
,
где Iq - общий индекс физического объема.
![]() .
.
Общий индекс товарооборота найдем, используя индексную факторную модель.
Поскольку товарооборот равен произведения цены товаров на объем продаж, то общий индекс товарооборота равен произведению общего индекса цен на общий индекс физического объема товарооборота:
Ipq = Ip · Iq., где Ipq - общий индекс товарооборота.
Т.о. общий индекс товарооборота:
Ipq = 0,765 · 1,097 = 0,839.
Т. к. общий индекс товарооборота меньше 1, то товарооборот в фактических ценах уменьшился на 16,1% (1 - 0,839 = 0,161)
Задача № 3.
Динамика себестоимости и объема продукции "А" на двух заводах характеризуется следующими данными:
Таблица 3. Выпуск продукции "А".
| Заводы | Себестоимость единицы продукции, тыс. руб. | Выработано продукции, тыс. руб. | ||
| Базис | Отчет | Базис | Отчет | |
| 1. | 4,0 | 3,4 | 2,0 | 3,0 |
| 2. | 3,5 | 3,0 | 3,0 | 5,0 |
На основании этих данных вычислите:
1. индекс себестоимости переменного состава;
2. индекс себестоимости постоянного состава;
3. индекс структурных сдвигов.
Покажите взаимосвязь исчисленных индексов.
Решение:
Индексом переменного состава в статистике называют отношение двух средних величин. Найдем индекс переменного состава по следующей формуле:
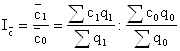 ,
,
где ![]() -
индекс переменного состава;
-
индекс переменного состава;
![]() и
и
![]() - средняя себестоимость в
отчетном и базисном периодах соответственно;
- средняя себестоимость в
отчетном и базисном периодах соответственно;
p1 и p0 - цена продукции в отчетном и базисном периодах соответственно.
q1 и q0 - объем продукции в отчетном и базисном периодах соответственно.
![]() .
.
Индекс себестоимости постоянного состава найдем как общий индекс по формуле:
 ,
,
где Iс - индекс себестоимости постоянного состава.
![]() .
.
Индекс структурных сдвигов найдем по формуле:
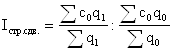 ,
,
где Iстр. сдв. - индекс структурных сдвигов.
![]() .
.
Индексы переменного, постоянного состава и структурных сдвигов связаны соотношением:
![]() =
Iс · Iстр. сдв.
=
Iс · Iстр. сдв.
Проверим: 0,854 · 0,996 = 0,851.
Малая величина индекса структурных сдвигов (-0,4%) говорит о том, что изменение соотношения объемов производства из-за структуры себестоимости менее ощутимо. Основное изменение затрат связано с уменьшением себестоимости продукции.
Задача №4
Имеются следующие данные по промышленному предприятию:
Таблица 4
| ПОКАЗАТЕЛИ | ТЫС. РУБ. |
| Полная первоначальная стоимость основных фондов на начало года | 6000 |
| Введено новых фондов в течении года | 1900 |
| Выбыло фондов | 800 |
| Численность рабочих, чел. | 8000 |
| Валовая продукция в сопоставимых ценах | 1950 |
Определить:
стоимость основных фондов на конец года;
среднегодовую стоимость основных фондов;
коэффициенты выбытия и обновления фондов;
фондоотдачу (2-мя способами).
Решение:
Стоимость основных фондов на конец года найдем прибавив к стоимости основных фондов на начало года (6000) стоимость новых введенных фондов (1900) и отняв стоимость выбывших фондов (800). Тогда стоимость основных фондов на коней года равна:
ОПФк = ОПФн + ОПФввед - ОПФвыб
ОПФк = 6000 + 1900 - 800 = 7100 тыс. руб.
Среднегодовая стоимость основных фондов равна полусумме стоимости основных фондов на начало и конец года:
![]() =
(ОПФн + ОПФк) / 2
=
(ОПФн + ОПФк) / 2
![]() =
(6000 + 7100) / 2 = 6550 тыс. руб.
=
(6000 + 7100) / 2 = 6550 тыс. руб.
Коэффициент выбытия основных фондов равен отношению стоимости выбывших основных фондов к стоимости основных фондов на начало года.
Квыб = ОПФвыб / ОПФн, Квыб = 800/6000 = 0,133
Коэффициент обновления основных фондов равен отношению стоимости введенных основных фондов к стоимости основных фондов на конец года.
Кобн = ОПФввед / ОПФк, Кобн = 1900/7100 = 0,267
Фондоотдача равна отношению стоимости валовой продукции к среднегодовой стоимости основных фондов.
Фо = PQ / ![]() , Фо = 1950/6550 = 0,2977
, Фо = 1950/6550 = 0,2977
Фондоемкость продукции равна отношению среднегодовой стоимости основных фондов к стоимости валовой продукции за год.
Фе = ![]() /
PQ
/
PQ
Фе = 6550/1950 = 3,359
Фондоотдача равна единице деленной на фондоемкость:
Фо = 1/Фе
Фо = 1/3,359 = 0,2977
Задача № 5
Фактическая стоимость реализованной продукции (в оптовых ценах предприятия) за полугодие составила 2090 тыс. руб. при плане 2005 тыс. руб. Определить выполнение плана по числу оборотов оборотных средств, если известны следующие данные о наличии оборотных средств (тыс. руб.)
Таблица 5
| Оборотные средства, тыс. руб. | ||
| По плану | Фактически | |
| на 1.07.95 | 410 | 400 |
| на 1.08.95 | 500 | 500 |
| на 1.09.95 | 500 | 510 |
| на 1.10 95 | 500 | 495 |
| на 1.11.95 | 510 | 505 |
| на 1.12.95 | 510 | 515 |
| на 1.01.96 | 510 | 508 |
Решение:
Средний уровень для моментного ряда рассчитывается по формуле:
![]() ;
;
Рассчитаем среднее значения стоимости оборотных средств за второе полугодие 1995 г.
![]() тыс. руб.
тыс. руб.
![]() тыс. руб.
тыс. руб.
Число оборотов оборотных средств найдем как отношение стоимости реализованной продукции к средней стоимости оборотных средств.
ОБплан = 2005/510 = 3,93
ОБфакт = 2090/497,3 = 4,2
Выполнение плана по числу оборотов:
4,2/3,93 · 100 = 106,87%
Задача № 6
Производство электроэнергии характеризуется следующими показателями:
Таблица 6.
| Год | Производство электроэнергии, млрд. квт. ч |
| 1 | 506,7 |
| 2 | 544,6 |
| 3 | 587,7 |
| 4 | 638,6 |
| 5 | 689,0 |
| 6 | 740,0 |
Для анализа ряда динамики рассчитайте:
1. показатели, характеризующие динамику производства энергии: абсолютный прирост, темпы роста и прироста, результаты расчетов изложите в табличной форме (табл.7);
2. средний уровень и среднегодовой темп ряда динамики;
3. покажите взаимосвязь между цепными и базисными показателями;
4. для определения основной тенденции ряда произведите выравнивание ряда динамики с помощью уравнения прямой.
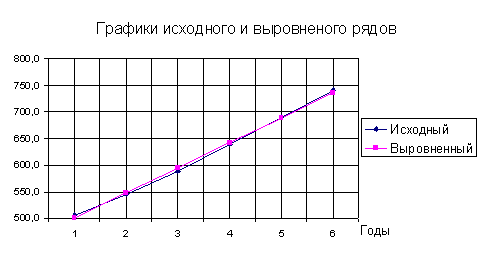
Изобразите первоначальный и выровненный динамические ряды.
Сделайте выводы.
Решение:
Рассчитаем показатели динамики по следующим формулам:
Абсолютный прирост базисный:
Di баз = Yi - Y1,
где Y1 - уровень производства электроэнергии в первый год, Yi - уровень производства электроэнергии в i-ый год. Абсолютный прирост цепной:
Di цеп = Yi - Yi-1,
где Yi-1 - уровень производства электроэнергии в предшествующий i-му год.
Ускорение: а2 = Di цеп - Di-1 цеп.. Темп роста базисный: Тр = (Yi / Y1) ·100.
Темп роста цепной: Тр = (Yi / Yi-1) ·100. Темп прироста базисный: Тпр = Тр - 100. Темп прироста цепной: Тпр = Тр - 100. Рассчитанные показатели сведем в таблицу:
Таблица 7. Показатели динамики производства электроэнергии
| Годы | Производство электроэнергии, млрд. квт. ч | Абсолютный прирост | Темп роста,% | Темп прироста,% | |||
| базисный | цепной | базисный | цепной | базисный | цепной | ||
| 1 | 506,7 | - | - | 100 | - | - | - |
| 2 | 544,6 | 37,9 | 37,9 | 107,48 | 107,48 | 7,48 | 7,48 |
| 3 | 587,7 | 81 | 43,1 | 115,99 | 107,91 | 15,99 | 7,91 |
| 4 | 638,6 | 131,9 | 50,9 | 126,03 | 108,66 | 26,03 | 8,66 |
| 5 | 689,0 | 182,3 | 50,4 | 135,98 | 107,89 | 35,98 | 7,89 |
| 6 | 740,0 | 233,3 | 51 | 146,04 | 107,40 | 46,04 | 7,40 |
Средний уровень для моментного ряда рассчитывается по формуле:
![]() ;
;
![]() .
.
Для определения среднегодового темпа роста воспользуемся формулой:
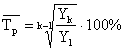 ,
,
где k - число субпериодов в ряду динамики.
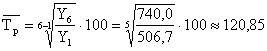
Явно видна взаимосвязь между цепными и базисными показателями только у абсолютного прироста.
Она вытекает из методов расчета этих показателей.
Т. е. базисный абсолютный прирост какого-либо года равен сумме всех цепных приростов от этого года до начала периода.
Т. к. темп роста вычисляется в процентах, то множитель 100 затеняет связь между показателями, если же перейти к коэффициенту роста равному темпу роста, деленному на 100, то видна взаимосвязь через произведение:
![]() или
или
![]() .
.
Для определения основной тенденции ряда произведем выравнивание ряда динамики с помощью уравнения прямой:
Yi теор = а0 + а1ti,
где Yi теор - рассчитанное выровненное значение производства электроэнергии, после подставления в уравнение значения ti. Для нахождения а0 и а1 решим следующую систему.
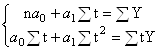
Для решения системы составим таблицу:
Таблица 8
| Годы | Производство электроэнергии, млрд. квт. ч | t | Y*t | t2 | f (t) |
| 1 | 506,7 | -5 | -2533,5 | 25 | 499,87 |
| 2 | 544,6 | -3 | -1633,8 | 9 | 547,03 |
| 3 | 587,7 | -1 | -587,7 | 1 | 594, 19 |
| 4 | 638,6 | 1 | 638,6 | 1 | 641,35 |
| 5 | 689,0 | 3 | 2067 | 9 | 688,51 |
| 6 | 740,0 | 5 | 3700 | 25 | 735,67 |
| Итого | 3706,6 | 0 | 1650,6 | 70 | 3706,6 |
а0 = 3706,6/6 = 617,8 и а1 = 1650,6/70 = 23,58.
Таким образом, f (t) = 617,8 + 23,58t, для t= -5, -3, …, +3, +5, или
f (t) = 452,7 + 47,16t, для t = 1, 2, 3, 4, 5,6. а1 = 47,16 - показатель силы связи, т.е. за период 6 лет происходило увеличение производства на 47,16% ежегодно. Изобразим исходный и выровненный ряды. Как видим, исходный ряд несильно отличается от выровненного, т.е. уравнение прямой адекватно отражает сложившуюся в ряду динамики тенденцию.
Задача №7
Из отчетов 26 предприятий отрасли получены следующие данные об их работе в отчетном периоде:
Таблица 9.Результаты работы предприятий
| Заводы, п/п | Продукция, в сопоставимых ценах, млрд. руб. | Стоимость основных производственных фондов, млрд. руб. |
| 1. | 7,1 | 7,3 |
| 2. | 2,9 | 4,1 |
| 3. | 14,0 | 10,7 |
| 4. | 4,8 | 7,3 |
| 5. | 15,7 | 12,5 |
| 6. | 11,8 | 8,4 |
| 6. | 16,1 | 11,5 |
| 8. | 16,6 | 12,7 |
| 9. | 10,2 | 7,8 |
| 10. | 0,6 | 0,7 |
| 11. | 0,9 | 0,9 |
| 12. | 2,6 | 2,5 |
| 13. | 5,5 | 5,6 |
| 14. | 4,1 | 4,0 |
| 15. | 4,9 | 4,8 |
| 16. | 0,9 | 1,0 |
| 17. | 1,3 | 1,2 |
| 18. | 6,4 | 5,2 |
| 19. | 2,8 | 2,5 |
| 20. | 0,8 | 0,9 |
| 21. | 0,7 | 0,8 |
| 22. | 4,9 | 3,9 |
| 23. | 12,1 | 10,6 |
| 24. | 12,2 | 11,7 |
| 25. | 11,8 | 10,7 |
| 26. | 8,5 | 6,1 |
С целью выявления зависимости между стоимостью основных производственных фондов и выпуском продукции произведите группировку заводов по размеру основных фондов, образовав к групп заводов с равными интервалами. Величину интервалов определите с помощью правила Стерджесса. По каждой группе подсчитайте:
число заводов;
стоимость основных производственных фондов - всего и в среднем на один завод;
стоимость валовой продукции - всего и в среднем на один завод;
фондоотдачу (в процентах).
Результаты представьте в групповой итоговой таблице 10. Сделайте выводы.
Исследуйте зависимость между стоимостью продукции (результативный признак - у) и стоимостью основных производственных фондов (факторный признак - х). На основании исходных данных:
1. постройте поле корреляции, составьте корреляционную таблицу, определив число интервалов по правилу Стреджесса, нанесите эмпирическую линию регрессии на поле корреляции и сделайте выводы о возможной форме связи;
2. в целях синтезирования моделей зависимостей задайте вид и вычислите параметры уравнения связи, нанесите полученную теоретическую линию регрессии на график.
3. для установления практической значимости модели вычислите возможные показатели тесноты связи (коэффициент детерминации, эмпирическое и теоретическое корреляционные отношения, линейный коэффициент корреляции);
4. оцените надежность полученных коэффициентов, сделайте выводы по п. п.2, 3, 4;
5. используя полученную модель, сделайте прогноз стоимости продукции для предприятия со стоимостью основных фондов 14 млрд. руб.
Решение:
Определим количество интервалов по правилу Стерджесса. Разделим выборку на L классов, где L = 1 + 3,322·lg (26) = 6. При группировке с равными интервалами для расчета длины одного интервала применяется формула:
![]() ,
,
где h - длина одного интервала;
xmax - максимальное значение группировочного признака;
xmin - минимальное значение группировочного признака;
Найдем длину интервала:
![]()
Найдем в какую группу попадает каждый завод и запишем ее номер в дополнительный столбец в таблице исходных данных. Рассчитаем требуемые параметры по группам и полученные значения сведем в таблицу:
Таблица 10.
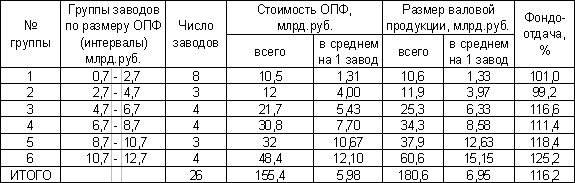
Итак, наибольшие стоимость ОПФ и размер валовой продукции имеет группа заводов №6, у заводов этой же группы наибольшее среднее значение размера валовой продукции и фондоотдачи.
Определим количество интервалов по правилу Стерджесса. Разделим выборку на L классов, где L = 1 + 3,322·lg (26) = 6.
Найдем длину интервала по размеру валовой продукции:
![]()
Составим корреляционную таблицу
| Х \ Y | 0,6 - 3,3 | 3,3 - 5,9 | 5,9 - 8,6 | 8,6 - 11,2 | 11,2 - 13,9 | 13,9 - 16,6 | Итого |
| 0,7 - 2,07 | 6 | 0 | 0 | 0 | 0 | 0 | 6 |
| 2,07 - 4,07 | 3 | 2 | 0 | 0 | 0 | 0 | 5 |
| 4,07 - 6,07 | 0 | 2 | 2 | 0 | 0 | 0 | 4 |
| 6,07 - 8,07 | 0 | 1 | 1 | 1 | 1 | 0 | 4 |
| 8,07-10,07 | 0 | 0 | 0 | 0 | 2 | 1 | 3 |
| 10,07-12,07 | 0 | 0 | 0 | 0 | 1 | 3 | 4 |
| Итого | 9 | 5 | 3 | 1 | 4 | 4 | 26 |
Построим поле корреляции и нанесем на него эмпирическую линию корреляции.
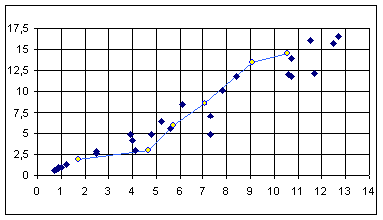
Анализируя поле корреляции и линию регрессии можем видеть, что зависимость имеет скорее всего линейный вид и связь сильная.
Запишем уравнение регрессии как
Yiтеор = a0 + a1Xi,
где Yiтеор - рассчитанное выравненное значение результативного признака после подстановки в уравнение Х. Параметры a0 и a1 найдем по формулам вытекающей из МНК:
a1 = ,a0 =
,a0 = ![]() .
.
Итак:
a1 = 1,26; a0 = 7,05 - 1,26 · 4,45 = 0,15.
Т. е. Yiтеор = 0,15 + 1,26·Xi.
Нанесем теоретическую линию регрессии на график
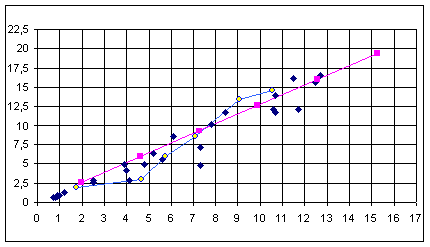
Коэффициент детерминации R2 рассчитывается по формуле
R2
=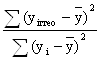 .
.
R2 = (67,68/80,65) = 0,84
Т. е. теоретическая регрессия на 84 процента совпадает с эмпирическими данными.
Теоретическое корреляционное отношение R равно корню квадратному из коэффициента детерминации:
R = ![]() = 0,916
= 0,916
Т. е. 91,6% вариации обусловлено различием между заводами.
Линейный коэффициент корреляции рассчитаем по формуле:
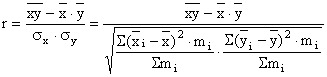 .
.
![]() .
.
Т.к. линейный коэффициент корреляции равен 0,643, то связь средняя или заметная. Надежность коэффициентов оценим по отношению:
 ;
; 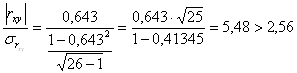
Т. к. отношение больше чем t = 2,56, то коэффициенты надежны.
Итак получена линейная модель Yiтеор = 0,15 + 1,26·Xi, которая будучи нанесенной на график достаточно хорошо характеризует выборку. Связанность факторного и результативного признака заметная и линейный коэффициент надежен.
Спрогнозируем по модели стоимость продукции для предприятия со стоимостью основных фондов 14 млрд. руб.
Y = 0,15 + 1,26·14 = 17,79 млрд. руб.