Курсовая работа: Расчет системы водоснабжения
Московский Государственный Университет Путей Сообщения
Институт Транспортной Техники и Организации Производства
(ИТТОП)
Кафедра: «Теплоэнергетика железнодорожного транспорта»
(ТЖТ)
Курсовая работа по дисциплине:
«Технологические энергоносители промышленных предприятий»
Выполнила:
Ст. гр. ТЭН-412
Проверил:
Москва 2009
Расчет системы водоснабжения
Необходимо:
- Построить график нагрузки сети и установить параметры режимов – максимального водопотребления и максимального транзита,
- Выбрать диаметры труб для участков сети, исходя из режима максимального транзита,
- Выполнить внутреннюю увязку сети для двух указанных режимов,
- Построить пьезометрические графики сети и вычислить характеристики водопитателей.
График нагрузки сети
Строится как сумма графиков потребления воды всеми потребителями. Режим максимального водопотребления соответствует часам максимальной нагрузки сети. В режиме максимального транзита нагрузки сети – минимально.
| Потребитель |
Расход, м3/с |
Геодезическая высота | |||
| 0-6 | 6-12 | 12-18 | 18-24 | ||
| 1 | 0,02 | 0,08 | 0,05 | 0,03 | 3,5 |
| 2 | 0,01 | 0,13 | 0,09 | 0,03 | 5,0 |
| 3 | 0,04 | 0,10 | 0,12 | 0,05 | 1,5 |
| 4 | 0,02 | 0,04 | 0,05 | 0,01 | 4,0 |
| 5 | 0,02 | 0,07 | 0,07 | 0,03 | 5,5 |
| НС | 0,5 | ||||
| Б | 10,5 | ||||
| ∑ | 0,11 | 0,42 | 0,38 | 0,15 |
Qср – среднесуточная нагрузка системы определяется интегрированием графика нагрузки сети по времени
![]()
![]() =(Q0-6*6+Q6-12*6+Q12-18*6+Q18-24*6)/24=(0,11+0,42+0,38+0,15)/4= 1,06/4=0,265
м3/с
=(Q0-6*6+Q6-12*6+Q12-18*6+Q18-24*6)/24=(0,11+0,42+0,38+0,15)/4= 1,06/4=0,265
м3/с
Эта величина равна производительности насосной станции при условии, что в течении суток вода подается насосами равномерно.
![]()
Поток воды в водонапорную башню при минимальной нагрузке сети Qсmin =0,11 м3/с (режим максимального транзита)
QБ= QН – Qсmin=0,265 – 0,11 = 0,155 м3/с
В часы максимального водопотребления башня отдает воду в сеть в количестве:
QБ=Qcmax – QНС=0,42 – 0,265=0,155 м3/с,
где Qcmax =0,42 м3/с – максимальная нагрузка сети
Выбор диаметров труб для участков сети
Режим максимального транзита (Qс=min) является определяющим для выбора диаметров. Вначале задается начальное потокораспределение, которое удовлетворяет первому закону Кирхгофа. Для этого, рассматривая конфигурацию сети, как граф, рекомендуется построить дерево графа путем удаления части участков сети, число которых равно n
n=p-m+1 (1),
где p- число участков, m – число узлов, n – количество элементарных контуров
n=9-7+1=3
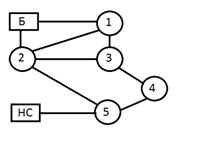
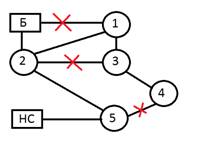
В результате сеть становится тупиковой (контуры в сети отсутствуют, n=0). Для нее просто задать начальное потокораспределение путем суммирования потребления воды, начиная с концевых узлов. На исключенных участках поток воды принимается равным нулю.

Для каждого i-того участка дерева диаметр труб выбирается из таблицы 1 по величине приведенного расхода qiп
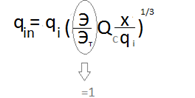 ,
,
где qi – поток на участке, м3/с
Э – действительный экономический фактор,
Эт – табличный экономический фактор,
х – доля единичного расхода на участке,
Единичный расход на участке:

Qс – нагрузка сети для рассматриваемого режима, м3/с (Qс=min):
1уч. НС-5 qп=0,265*(0,11*0,3/0,265)1/3= 0,198 м3/с=198 литр/с → D=450мм=0,45м
2уч. 5-2 qп=0,245*(0,11*1/0,245) 1/3=0,189 м3/с=189 литр/с → D=450мм=0,45м
3уч. 2-Б qп=0,155*(0,11*0,7/0,155) 1/3=0,123 м3/с=123 литр/с → D=350мм=0,35м
4уч. 2-1 qп=0,08*(0,11*0,3/0,08) 1/3=0,060 м3/с=60 литр/с → D=250мм=0,25м
5уч. 1-3 qп=0,06*(0,11*0,3/0,06) 1/3=0,040 м3/с=49 литр/с → D=250мм=0,25м
6уч. 3-4 qп=0,02*(0,11*0,3/0,02) 1/3=0,024 м3/с=24 литр/с → D=175мм=0,175м
Диаметры исключенных участков принимаются равными средним значениям диаметров тех участков, которые они соединяют.
7уч. Б-1 D=(D2-Б+D2-1)/2=(0,35+0,25)/2=0,3м
8уч. 3-2 D=(D1-2+D1-3)/2=(0,25+0,25)/2=0,25м
9уч. 5-4 D=(D2-5+D3-4)/2=(0,45+0,175)/2=0,3125≈0,3м
Режим минимального транзита (Qс=max) :
1уч. НС-5 qп=0,265*(0,42*1/0,265)1/3= 0,309 м3/с=309 литр/с
2уч. 5-2 qп=0,245*(0,42*1/0,245) 1/3=0,293 м3/с=293 литр/с
3уч. 2-Б qп=0,155*(0,42*0,7/0,155) 1/3=0,192 м3/с=192 литр/с
4уч. 2-1 qп=0,08*(0,42*0,3/0,08) 1/3=0,093 м3/с=93 литр/с
5уч. 1-3 qп=0,06*(0,42*0,3/0,06) 1/3=0,077 м3/с=77 литр/с
6уч. 3-4 qп=0,02*(0,42*0,3/0,02) 1/3=0,037 м3/с=37 литр/с
Внутренняя увязка сети:
Увязка выполняется по методу Лобачева-Кросса. Для каждого участка сети вычисляется гидравлическая характеристика si
![]()
где Di – диаметр трубы, м; Li – длина участка, м; а – коэффициент, учитывающий местные сопротивления.
Падение давления на участке связано с расходом квадратической зависимостью
pi=siqi2
где pi – падения давления, м вод ст; si – гидравлическая характеристика; qi – расход воды на участке, м3/с
По соотношению Эйлера (1) определяется количество элементарных контуров сети. Увязка выполняется следующих образом:
1. Для каждого участка сети задается положительное направление потока и его величина, причем все потоки на участках должны удовлетворять первому закону Кирхгофа; для этого удобно рассматривать его как нулевое приближение,
2. В каждом контуре вычисляется невязка ∆hn, определяющая меру несоответствия потоков воды в сети второму закону Кирхгофа,
∆hn=∑siqiabs(qi)
Суммирование выполняется по участкам сети, составляющим контур, с учетом знаков и направления обхода, принятых при формулировке второго закона Кирхгофа,
3. Если модуль максимальной невязки меньше допустимой величины, увязка заканчивается; в противном случае процесс итераций продолжается,
4. Для каждого контура вычисляется поправка ∆qn, положительное направление которой противоположно обходу контура по второму закону Кирхгофа
![]()
Суммирование в знаменателе выполняется по участкам контура,
5. Контурные поправки используются для коррекции значений потоков воды на участках
qik+1=qik+∑∆qn
Суммируются поправки только тех контуров, в состав которых входит рассматриваемый участок; суммирование выполняется с учетом направлений, принятых для потоков и контурных поправок; далее вычисления повторяются, начиная с пункта 2.

По программе получилось, что выбранные направления на участках 5,6,8,9 надо изменить на противоположные. Это будет выглядеть так:

Пьезометрический график
|
Номер узла |
Геодез. Высота Z, м |
Свободный Напор (предвар) Н,м |
Пьез. Высота (предвар) П, м |
Н, м |
П, м |
|
НС |
0,5 | 32,636 | 33,136 | 63,8 | 64,3 |
|
1 |
3,5 | 1,504 | 5,004 | 21,5 | 25 (дикт) |
|
2 |
5,0 | 19 | 24 | 38,996 | 43,996 |
|
3 |
1,5 | 21,728 | 23,228 | 41,724 | 43,224 |
|
4 |
4,0 | 20 | 24 (дикт) | 51,164 | 55,164 |
|
5 |
5,5 | 18,453 | 23,953 | 49,617 | 55,117 |
|
Б |
10,5 | -5,507 | 4,993 | 14,489 | 24,989 |
Выбираю диктующего потребителя: 4. Задаю П4=24 м, H4=П4-z4=24-4=20 м
П5=П4-∆p4-5=24-0,047=23,953
П3=П4-∆p3-4=24-0,772=23,228
П1=П3-∆p1-3=23,228-18,224=5,004
П2=П3+∆p2-3=23,228+0,772=24
![]()
ПНС=П5+∆pНС-5=23,953+9,183=33,136
ПБ=П1-∆pБ-1=5,004-0,001=5,003
ПБ=П2-∆pБ-2=24-19,017=4,983 ПБ≈4,993
ННС=ПНС-zНС=33,136-0,5=32,636
Н1=П1-z1=5,004-3,5=1,504
Н2=П2-z2=24-5=19
Н3=П3-z3=23,228-1,5=21,728
Н5=П5-z5=23,953-5,5=18,453
НБ=ПБ-zБ=4,993-10,5= -5,507
Минимальный свободный напор получился для потребителя 1
Принимаю П1=25м
П3=П1+∆p1-3=25+18,244=43,224
П2=П3+∆p2-3=43,224+0,772=43,996
П4=П3+∆p3-4=43,224+11,940=55,164
П5=П4-∆p4-5=55,164-0,047=55,117
![]()
ПНС=П5+∆pНС-5=55,117+9,183=64,3
ПБ=П1-∆pБ-1=25-0,001=24,999
ПБ=П2-∆pБ-2=43,996-19,017=24,979 ПБ≈24,989
ННС=ПНС-zНС=64,3-0,5=63,8
Н1=П1-z1=25-3,5=21,5
Н2=П2-z2=43,996-5=38,996
Н3=П3-z3=43,224-1,5=41,724
Н4=П4-z4=55,164-4=51,164
Н5=П5-z5=55,117-5,5=49,617
НБ=ПБ-zБ=24,989-10,5=14,489
Характеристики водопитателей
Рабочий объем водонапорной башни Vp находится с помощью графика нагрузки сети. Необходимо вычислить интеграл
Vp=ʃ(Qc(τ)-Qc)d τ=6*[(0,42-0,265)+(0,38-0,265)]=1,62 м3
Если диаметр бака башни и максимальный уровень его заполнения относятся как 2:1, то с учетом 10% запаса воды диаметр бака равен
DБ=1,46Vp1/3=1,46*1,61/3=1,715 м,
h0=,5*DБ=0,8575 м
где h0 – максимальный уровень заполнения бака водой,
DБ – диаметр бака
Vp – рабочий объем
H’НС=Нтр+(zA-zНС)+∑∆p’i=20+(3,5-,5)+89,434=112,434
H”НС=HБ+(zБ-zНС)+h0+∑∆p’’i=14,489+(10,5-0,5)+0,8575+36,907=62,2535
Где ∆p’ падения давления при Qc=max, ∆p’’ падения давления при Qc=min, а
HБ, H’НС – max ; H”НС – min
Итоговая таблица
| Уч | D, м | L, м |
q’, м3/с |
q’’,м3/с |
∆p’, м вод ст | ∆p’’, м вод ст |
| 1 (НС-5) | 0,45 | 700 | 0,309 | 0,198 | 9,183 | 3,771 |
| 2 (5-2) | 0,45 | 900 | 0,301 | 0,194 | 11,215 | 4,671 |
| 3 (2-Б) | 0,35 | 1000 | 0,191 | 0,123 | 19,017 | 7,817 |
| 4 (2-1) | 0,25 | 800 | 0,088 | 0,056 | 19,015 | 7,817 |
| 5 (1-3) | 0,25 | 850 | 0,083 | 0,053 | 18,244 | 7,472 |
| 6 (3-4) | 0,175 | 700 | 0,029 | 0,019 | 11,940 | 4,995 |
| 7 (Б-1) | 0,3 | 650 | 0,001 | 0,000 | 0,001 | 0,000 |
| 8 (3-2) | 0,25 | 1200 | 0,014 | 0,010 | 0,772 | 0,344 |
| 9 (5-4) | 0,3 | 600 | 0,008 | 0,005 | 0,047 | 0,020 |
| ∑ |
89,434 |
36,907 |
Где ∆p’ и q’- падения давления и расход при Qc=max, а ∆p’’ и q” - падения давления и расход при Qc=min
| Газопровод среднего давления | ||||||||
| потребитель | Расход по часам суток, куб.м /час | |||||||
| 0-6 | 6-12 | 12-18 | 18-24 | |||||
| 1 | 150 | 550 | 400 | 200 | ||||
| 2 | 200 | 950 | 750 | 250 | ||||
| 3 | 150 | 400 | 800 | 100 | ||||
| 4 | 100 | 500 | 550 | 200 | ||||
| 5 | 250 | 850 | 850 | 150 | ||||
| 6 | 100 | 150 | 150 | 100 | ||||
| 7 | 100 | 200 | 250 | 100 | ||||
| 8 | 150 | 350 | 250 | 200 | ||||
| 9 | 200 | 100 | 200 | 100 | ||||
| сумма | 1400 | 4050 | 4200 | 1400 | ||||
| Газопровод низкого давления | ||||||||
| потребитель | Расход по часам суток, куб.м /час | |||||||
| 0-6 | 6-12 | 12-18 | 18-24 | |||||
| 6 | 100 | 150 | 150 | 100 | ||||
| 7 | 100 | 200 | 250 | 100 | ||||
| 8 | 150 | 350 | 250 | 200 | ||||
| 9 | 200 | 100 | 200 | 100 | ||||
| сумма | 550 | 800 | 850 | 500 |
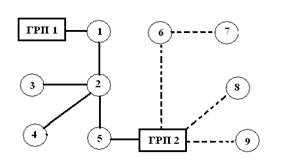
Диаметры труб участков сети выбираются с помощью номограммы, исходя из найденного оптимального pi , а также Li , и расхода газа Vi
| Участок | Длина, м |
Расход, м3/ч |
Удельные потери, Па/м | Диаметр стандартный, м |
| 1 – ГРП1 | 900 | |||
| 1 - 2 | 900 | |||
| 2 - 3 | 1000 | |||
| 2 - 4 | 550 | |||
| 2 - 5 | 750 | |||
| 5 – ГРП2 | 500 | |||
| 6 – ГРП2 | 250 | |||
| 6 - 7 | 400 | |||
| 6 - 8 | 150 | |||
| 9 – ГРП 2 | 250 |
Испр_max
N=9
DIM flux(N), diam(N), length(N),s(N), press(N)
READ dHmin, a
DATA 0.001, 0.15
for i=1 to N
READ b
flux(i)=b
READ b
length(i)=b
READ b
diam(i)=b
NEXT i
DATA 0.309, 700, 0.450
DATA 0.293,900, 0.450
DATA 0.192,1000, 0.350
DATA 0.093, 800,0.250
DATA 0.077, 850,0.250
DATA 0.037, 700, 0.175
DATA 0, 650, 0.300
DATA 0, 1200, 0.250
DATA 0, 600, 0.300
for i=1 to N
s(i)=0.001735*(1+a)*length(i)/diam(i)^5.3
next i
[A]
dH1=s(3)*flux(3)*Abs(flux(3))-s(7)*flux(7)*Abs(flux(7))-s(4)*flux(4)*Abs(flux(4))
dH2=s(4)*flux(4)*Abs(flux(4))-s(5)*flux(5)*Abs(flux(5))-s(8)*flux(8)*Abs(flux(8))
dH3=s(2)*flux(2)*Abs(flux(2))+s(8)*flux(8)*Abs(flux(8))-s(6)*flux(6)*Abs(flux(6))-s(9)*flux(9)*Abs(flux(9))
if Abs(dH1)<dHmin and Abs(dH2)<dHmin and Abs(dH3)<dHmin goto [B]
dq1=0.5*dH1/(s(4)*Abs(flux(4))+s(7)*Abs(flux(7))+s(3)*Abs(flux(3)))
dq2=0.5*dH2/(s(4)*Abs(flux(4))+s(5)*Abs(flux(5))+s(8)*Abs(flux(8)))
dq3=0.5*dH3/(s(8)*Abs(flux(8))+s(2)*Abs(flux(2))-s(9)*Abs(flux(9))+s(6)*Abs(flux(6)))
flux(1)=flux(1)
flux(2)=flux(2)-dq3
flux(3)=flux(3)-dq1
flux(4)=flux(4)+dq1-dq2
flux(5)=flux(5)+dq2
flux(6)=flux(6)+dq3
flux(7)=flux(7)+dq1
flux(8)=flux(8)+dq2-dq3
flux(9)=flux(9)-dq3
goto [A]
[B]
for i=1 to N
press(i)=s(i)*flux(i)*Abs(flux(i))
next i
for i=1 to N
PRINT "i="; i;
PRINT ";lenght="; length(i);
PRINT ";diam="; diam(i);
PRINT ";flux="; using ("#.###", flux(i));
PRINT ";press="; using ("##.###", press(i))
next i
PRINT "dH1="; using ("#.#####", dH1) ;";dH2="; using ("##.#####",dH2); ";dH3="; using("#.#####", dH3)
end
Испр_min
N=9
DIM flux(N), diam(N), length(N),s(N), press(N)
READ dHmin, a
DATA 0.001, 0.15
for i=1 to N
READ b
flux(i)=b
READ b
length(i)=b
READ b
diam(i)=b
NEXT i
DATA 0.198, 700, 0.450
DATA 0.189,900, 0.450
DATA 0.123,1000, 0.350
DATA 0.060, 800,0.250
DATA 0.049, 850,0.250
DATA 0.024, 700, 0.175
DATA 0, 650, 0.300
DATA 0, 1200, 0.250
DATA 0, 600, 0.300
for i=1 to N
s(i)=0.001735*(1+a)*length(i)/diam(i)^5.3
next i
[A]
dH1=s(3)*flux(3)*Abs(flux(3))-s(7)*flux(7)*Abs(flux(7))-s(4)*flux(4)*Abs(flux(4))
dH2=s(4)*flux(4)*Abs(flux(4))-s(5)*flux(5)*Abs(flux(5))-s(8)*flux(8)*Abs(flux(8))
dH3=s(2)*flux(2)*Abs(flux(2))+s(8)*flux(8)*Abs(flux(8))-s(6)*flux(6)*Abs(flux(6))-s(9)*flux(9)*Abs(flux(9))
if Abs(dH1)<dHmin and Abs(dH2)<dHmin and Abs(dH3)<dHmin goto [B]
dq1=0.5*dH1/(s(4)*Abs(flux(4))+s(7)*Abs(flux(7))+s(3)*Abs(flux(3)))
dq2=0.5*dH2/(s(4)*Abs(flux(4))+s(5)*Abs(flux(5))+s(8)*Abs(flux(8)))
dq3=0.5*dH3/(s(8)*Abs(flux(8))+s(2)*Abs(flux(2))-s(9)*Abs(flux(9))+s(6)*Abs(flux(6)))
flux(1)=flux(1)
flux(2)=flux(2)-dq3
flux(3)=flux(3)-dq1
flux(4)=flux(4)+dq1-dq2
flux(5)=flux(5)+dq2
flux(6)=flux(6)+dq3
flux(7)=flux(7)+dq1
flux(8)=flux(8)+dq2-dq3
flux(9)=flux(9)-dq3
goto [A]
[B]
for i=1 to N
press(i)=s(i)*flux(i)*Abs(flux(i))
next i
for i=1 to N
PRINT "i="; i;
PRINT ";lenght="; length(i);
PRINT ";diam="; diam(i);
PRINT ";flux="; using ("#.###", flux(i));
PRINT ";press="; using ("##.###", press(i))
next i
PRINT "dH1="; using ("##.#####", dH1) ;";dH2="; using ("##.#####",dH2); ";dH3="; using("##.#####", dH3)
end