Курсовая работа: Розрахунок двошарнірної арки методом сил
Полтавський національний технічний університет
імені Юрія Кондратюка
Факультет будівельний
Кафедра будівельної механіки
РОЗРАХУНКОВО-ГРАФІЧНА
Полтава 2010
Зміст
1. Кінематичний аналіз заданої системи та визначення кількості невідомих методу сил
2. Вибір основної системи методу сил
3. Запис канонічного рівняння методу сил
4. Визначення коефіцієнта і вільного члена канонічного рівняння методу сил і їх перевірка
5. Розв’язання канонічного рівняння методу сил
6. Побудова епюр внутрішніх зусиль для заданої арки та перевірка
Література
Додаток А. Графічний матеріал роботи: Епюри внутрішніх зусиль для заданої арки
Вихідні дані
l = 12 м; 
= 0,20 = 2,4 м; EaIa = 34×104 кПа×м4;
q1 = 18 кН/м; q2 = 18 кН/м; F1= 180 кН.
Окреслення осі
арки по квадратній параболі: 
Розрахункова схема
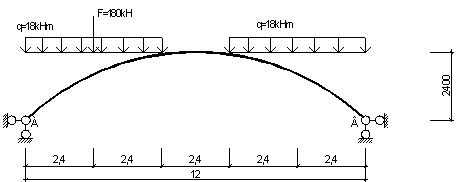
1. Кінематичний аналіз.
а). Визначимо ступінь свободи системи:
,
де Д – кількість дисків;
Ш – кількість простих шарнірів;
В0 – кількість опорних в’язей.
Ступінь статичної
невизначеності системи 
.
Отже, дана арка є один раз статично невизначною (має 1 невідоме методу сил) і може бути геометрично незмінна.
б). Аналіз геометричної структури заданої рами.
Дана арка складається із одного криволінійного елементу, який опирається на нерухому основу за допомогою чотирьох опорних в’язей (на дві шарнірно-нерухомі опори) і є геометрично незмінна.
Двошарнірна арка є розпірною системою, оскільки при дії вертикального навантаження виникають горизонтальні складові опорних реакцій, які називають розпором і позначають – Н.
2. Вибираємо основну систему методу сил шляхом відкидання зайвої в’язі, навантаживши при цьому її зовнішніми силами та зусиллям відкинутої зайвої в’язі - Х1.
Х1 є основне невідоме методу сил.
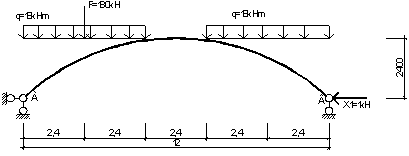
3.Для основної системи методу сил канонічне рівняння матиме вигляд:
d11×Х1 + D1F = 0;
де Х1 – основне невідоме методу сил (величина розпору);
d11 – переміщення перерізу, де прикладена Х1 в напрямку Х1, від Х1 = 1;
D1F – переміщення перерізу, де прикладена Х1, у напрямку Х1, від зовнішнього навантаження або інших впливів.
Зміст канонічного рівняння полягає в тому, що переміщення перерізу , де прикладена невідома Х1, в напрямку невідомої Х1, від зовнішнього навантаження дорівнює нулю. Тобто цим рівнянням ми заперечуємо взаємне зближення перерізів А і В.
4. Визначення коефіцієнта і вільного члена канонічного рівняння методу сил і їх перевірка.
4.1Значення d11 обчислюється за формулою:
де 
- внутрішні зусилля в арці
від Х1 = 1;
m - коефіцієнт, що враховує форму поперечного перерізу арки;
- відповідні жорсткості арки
та затяжки.
При розрахунку двошарнірних арок із постійними жорсткостями, осі яких окреслені за квадратною параболою, можна скористатися такими спрощеннями:
-
при
співвідношенні висоти перерізу арки до її прольоту 
,
а також 
нехтують поперечними та поздовжніми
силами при
обчисленні коефіцієнта і вільного члена канонічного рівняння методу сил;
-
коли 
, тоді інтегрування за
довжиною дуги арки , при обчисленні коефіцієнта і вільного члена канонічного
рівняння методу сил, змінюється інтегруванням за горизонтальною проекцією арки
(dS
dx).
В цьому разі d11 обчислюємо так:
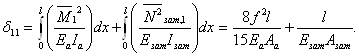
Для арки без затяжки:
Отже , переміщення перерізу:
4.2.1 При розрахунку двошарнірних арок із постійними жорсткостями, осі яких окреслені за квадратною параболою, у випадку, коли можна скористатися спрощеннями, що вказані вище, значення D1F обчислюється за формулою:
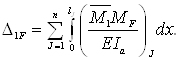
Побудуємо для
заданої арки епюру внутрішніх зусиль від одиничного значення невідомого – 
.
Так, як вісь арки
окреслюється по квадратній параболі, то значення 
визначимо,
як:
Якщо використати принцип незалежності дії сил, можна записати:
D1F = D1F1 + D1g1 +D1g2 ;
Таким чином, визначимо переміщення, де прикладене невідоме зусилля Х1 від кожного виду заданного навантаження.
Розглянемо Ділянку АО 0 ≤ х ≤ 4,8 Ділянка ВО 0 ≤ х ≤ 7,2
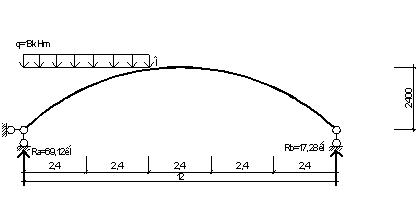
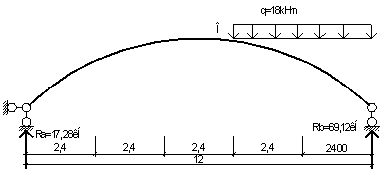
Розглянемо ділянку АО 0 ≤ х ≤ 7,2
Ділянка В0
0 ≤ х ≤ 4,8
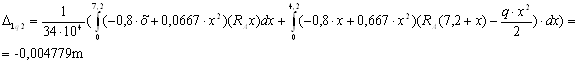
Розглянемо ділянку АО
0 ≤ х ≤ 2,4
Ділянка ВО
0 ≤ х ≤ 9,6
Маємо:
D1F = -0,011 – 0,004779 – 0,005
=
(м).
5. Розв’язання канонічного рівняння методу сил
d11×Х1 + D1F = 0;
Звідси: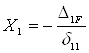
;
Після визначення з канонічного рівняння невідомого Х1, його значення перевіряємо за допомогою рівняння лінії впливу Х1 для двошарнірних арок з постійними жорсткостями, осі яких окреслені за квадратною параболою (у випадку коли можна скористатися спрощеннями, що вказані вище).
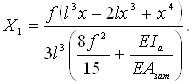
Для заданої арки без затяжки розпір Х1 обчислюється з умови, що ЕАзат = ∞.
В цьому разі:
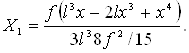
Від дії рівномірно розподіленого по довжині навантаження - g1.
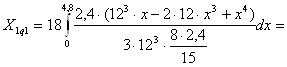46.742кН
Від дії – g2.
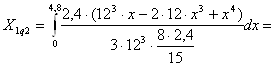13.003кН
Від дії зосередженої сили - F1 (x = 5,6)
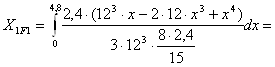130.032кН
Значення X1 визначене вірно. Х1=191,68кН
Подальший розрахунок ведемо в табличній формі. Для цього розбиваємо арку на n = 20 кількість ділянок та визначаємо тригонометричні характеристики в кожному конкретному перерізі, згідно формул:
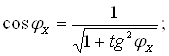
Далі проводимо аналогію – задаємось аркою такого самого прольоту, як і арка і з таким же навантаженням та визначаємо для неї внутрішні зусилля в кожному перерізі.
Маючи балочні внутрішні зусилля використовуємо формулу для визначення внутрішніх зусиль в перерізах двошарнірної арки.
Література
1. Смирнов А.Ф., Александров А.В., Лащеников Б.Я., Шапошников Н.Н. Строительная механика стержневых систем. – М.: Стройиздат, 1981.
2. Дарков А.В., Шапошников Н.Н. Строительная механика. – 8-е изд., перераб. и доп. – М.: Высшая школа, 1986.
3. Киселев В.А. Строительная механика, общий курс – 4-е изд., исправленное и доп. – М.: Стройиздат, 1986.
4. Бутенко Ю.И., Канн С.Н., Пустовойтов В.П. и др. Строительная механика стержневых систем и оболочек. – К.: Вища школа, 1980.
5. Строительная механика. Руководство к практическим занятиям / Под ред. Ю.И. Бутенко. – К.: Вища школа, 1989.
6. Руководство к практическим занятиям по курсу строительной механики (статически определимые и неопределимые системы) / Под ред. Г.К. Клейна. – 3-е изд., перераб. и доп. – М.: Высшая школа, 1973.
7. Методичні вказівки та контрольні завдання з дисципліни „Будівельна механіка (спецкурс)” для студентів денної форми навчання. Частина 2 (статично невизначні системи) / Полтава: ПНТУ, 2003. Укладачі: О.А. Шкурупій, Б.П. Митрофанов, А.М. Пащенко.
Додаток А
