Курсовая работа: Передача дискретных сообщений
ИСХОДНЫЕ ДАННЫЕ ДЛЯ КУРСОВОЙ РАБОТЫ
Скорость модуляции:
В= 1200 Бод;
Скорость распространения сигнала по каналу связи:
v = 80000км/с;
Среднее время наработки на отказ группового устройства:
Тгу= 1500ч;
Среднее время восстановления группового устройства:
tгу = 1.5 ч;
Среднее время восстановления устройства защиты от ошибок :
tузо = 0.33ч;
Среднее время восстановления УПС:
tупс = 0.33ч;
Вероятность ошибки в дискретном канале:
Ро ш= 0 .0005 и 0.005;
Элементная база 555;
Уровень сигнала на выходе канала:
Рс в ы х=-44.4 дБ;
Принципиальная схема - распредилитель;
Вид модуляции - ЧМ;
Эффективное значение аддитивной флуктуационной помехи:
Uп эф = 1.0 мВ;
Время восстановления работоспособности:
Тв = 0.5ч;
Вероятность необнаруженной ошибки: Рно=3,0×10-6
Расстояние между оконечными станциями: L=5500 км
Коефициент груповых ошибок a=0.55
Минимальная кодовае ростояние циклического кода d0=4
Время нароботки на отказ Tузо,ч=350
Время нароботки на отказ Тупс,ч=500
Коефициент готовности Кг=0.95
Вероятность безотказной работы на протяжении 12 ч. Не менее
Р (t=12ч)=0.915
1. Модели частичного описания дискретного канала
В реальных каналах связи ошибки возникают по многим причинам. В проводных каналах наибольшее количество ошибок вызывается кратковременными прерываниями и импульсными помехами. В радиоканалах заметное влияние оказывают флуктуационные шумы. В коротковолновых радиоканалах основное количество ошибок возникает при изменениях уровня сигнала вследствие влияния замирания. Во всех реальных каналах ошибки распределяются во времени очень неравномерно, из-за этого неравномерны и потоки ошибок.
Существует большое количество математических моделей дискретного канала. Также помимо общих схем и частных моделей дискретного канала, существует большое число моделей, дающих частичное описание канала. Остановимся на одной из таких моделей модели А. Л. Пуртова.
Формула модели дискретного канала с независимыми ошибками.
![]()
Ошибки несут пакетный характер, поетому вводится коефициент a
По этой модели можно определить зависимость вероятности появления искаженной комбинации от ее длины n и вероятность появления комбинаций длиной n с t ошибками(t<n).
Вероятность P( >1,n) является неубывающей функцией n.
При n=1 P(>1,n)=pош
При n вероятность P(>1,n)
Вероятность появления искажений кодовой комбинации длиной n
![]()
Где a -- показатель
группирования ошибок.
При a®0 имеем случай независимого появления ошибок, а при a®1 появление групповых ошибок (при a=1 вероятность искажений кодовой комбинации не зависит от n, так как в каждой ошибочной комбинации все елементы приняты с ошибкой) Наибольшее значение d(0,5 до 0,7) наблюдается, на КЛС, поскольку кратковременное прерывание приводит к появлению групп с большей плотностью ошибок. В радиорелейных линиях, где наряду с интервалами большой плотности ошибок наблюдается интервалы с редкими ошибками, значение d лежит в пределах от 0,3 до 0,5. В КВ радиотелеграфных каналах показатель группирования ошибок самый небольшой(0,3-0,4).
Распределение ошибок в комбинациях различной длины
![]()
оценивает не только вероятность появления искаженных комбинаций(хотя бы одна ошибка), но и вероятность комбинаций длиной n с t наперед заданными ошибками P(>t,n).
Следовательно, группирование ошибок приводит к увеличению числа кодовых комбинаций, пораженную ошибками большей кратности. Анализируя все выше сказанное, можно заключить, что при группирование ошибок уменьшается число кодовых комбинаций заданной длины n. Это понятно также из чисто физических соображений. При одном и том же числе ошибок пакетирование приводит к сосредоточению их на отдельных комбинациях, (кратность ошибок возрастает), а число искаженных кодовых комбинаций уменьшается.
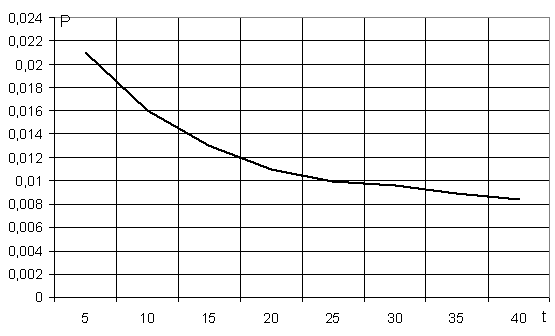
Графики зависимости необнаруженой ошибки в блоке от его длины.
Вероятность Р1=0.0005; Р2=0.005
![]()
![]()
получаем Рис 1.
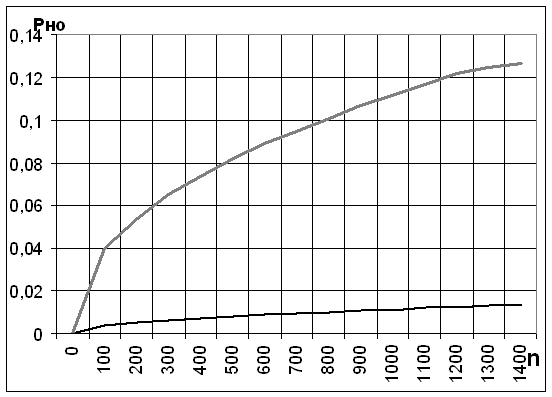
|
|||
|
Расчёт вероятности ошибки на выходе канала связи для ЧМ выполним по формулам:

где
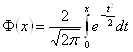 – функция Крампа;
– функция Крампа;
Уровень выходного сигнала Uп.эф =1.0 мВ
По условию нам задан уровень мощности сигнала на выходе канала связи: Pс.вых= -44.4 дБ. Зная уровень сигнала по напряжению (U0 = 0,775 В) найдём напряжение сигнала по формуле:
![]()
Тогда :
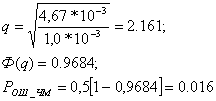
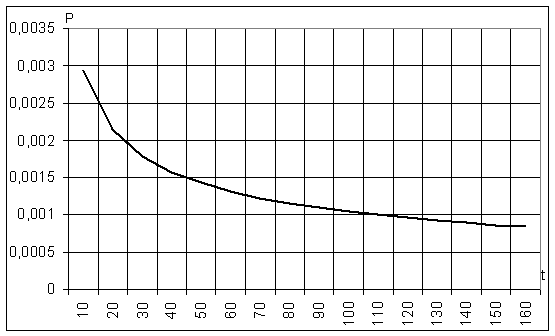
Построим графики зависимости вероятностей ошибок в блоке в зависимости от его длины.
Вероятность Р=0.016
![]() ;
; ![]()
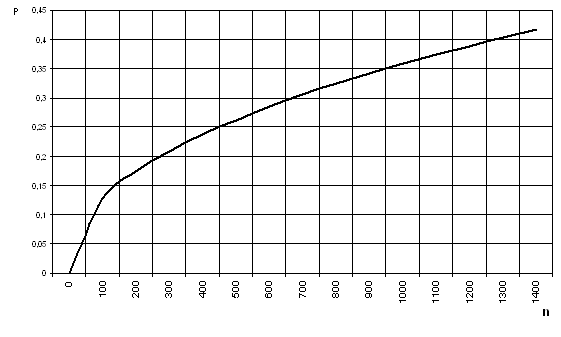 |
Рис Зависимость вероятности ошибки от длины блока.
2. СИСТЕМА С РОС И НЕПРЕРЫВНОЙ ПЕРЕДАЧЕЙ ИНФОРМАЦИИ (РОС-нп)
Построить структурную схему системы с РОСнп и блокировкой и описать алгоритм её функционирования использовав временные диаграммы.
В системах с РОС-нп передатчик передает непрерывную последовательность комбинаций, не ожидая получения сигналов подтверждения. Приемник стирает лишь те комбинации, в которых решающее устройство обнаруживает ошибки, и по ним дает сигнал переспроса. Остальные комбинации выдаются ПИ по мере их поступления. При реализации такой системы возникают трудности, вызванные конечным временем передачи и распространения сигналов. Если в некоторый момент времени закончен прием кодовой комбинации 2, в которой обнаружена ошибка, то к этому моменту времени по прямому каналу уже ведется передача следующей кодовой комбинации. Если время распространения сигнала в канале tc превышает длительность кодовой комбинации nto, то к моменту t’ может закончиться передача одной или нескольких комбинаций, следующих за второй. Еще некоторое число кодовых комбинаций будет передано до того времени (t’), пока будет принят и проанализирован сигнал переспроса по второй комбинации.
Таким
образом, при непрерывной передаче за время между моментом обнаружения ошибки
(t’) и приходом повторенной кодовой комбинации (t"’) будет принято еще h
комбинаций, где ![]()
где символ [х] означает наименьшее целое число, большее или равное х.
Так как передатчик повторяет лишь комбинации, по которым принят сигнал переспроса, то в результате повторения с запаздыванием на h комбинаций порядок следования комбинаций в информации, выдаваемой системой ПИ, будет отличаться от порядка поступления кодовых комбинаций в систему. Но получателю кодовые комбинации должны поступать в том же порядке, в котором они передавались. Поэтому для восстановления порядка следования комбинаций в приемнике должны быть специальное устройство и буферный накопитель значительной емкости (не менее ih, где i — число повторений), поскольку возможны многократные повторения.
Во избежание усложнения и удорожания приемников системы с РОС-нп строят в основном таким образом, что после обнаружения ошибки приемник стирает комбинацию с ошибкой и блокируется на h комбинаций (т.е. не принимает h последующих комбинаций), а передатчик по сигналу переспроса повторяет h последних комбинаций (комбинацию с ошибкой и h—1, следующий за ней). Такие системы с РОС-нп получили название систем с блокировкой РОС-нпбл. Эти системы позволяют организовать непрерывную передачу кодовых комбинаций с сохранением порядка их следования. Временная диаграмма (рис. 2.3) иллюстрирует работу системы с РОС-нпбл при обнаружении ошибки во второй комбинации в случае h=4. Как видно из диаграммы, передача комбинаций ИИ осуществляется непрерывно до момента получения передатчиком сигнала переспроса (после передачи пятой комбинации). После этого передача информации от ИИ прекращается на время h и четыре комбинации (начиная со второй и h—1=3 последующие) передаются из накопителя передатчика. Заметим, что его емкость должна быть равна/г комбинациям, т, е. kh бит. В это время в приемнике стираются h комбинаций: вторая комбинация, в которой обнаружена ошибка (отмечена звездочкой на рис. 2.3) и три последующие комбинации (заштрихованы на рисунке). Получив переданные из накопителя комбинации (от второй до пятой включительно) приемник выдает их ПИ, а передатчик продолжает передачу шестой и последующих комбинаций.
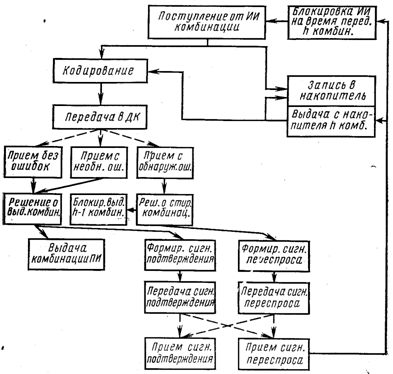
Рис. 2.2. Структурная схема алгоритма системы с РОС-нпбл
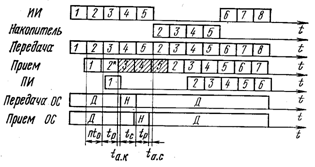
Рис. 2.3. Временные диаграммы работы системы с РОС-нпол
Хранение в передатчике каждой комбинации до получения сигнала подтверждения правильности приема (нуля) осуществляется в запоминающем устройстве. Переспрос реализуется передачей единицы. При этом кодовая комбинация, во время передачи которой принят сигнал переспроса, преднамеренно искажается передатчиком путем инвертирования последнего бита. Работу системы с циклической нумерацией в случае h=2 иллюстрирует временная диаграмма рис. 2.4. При этом рис. 2.4а соответствует случаю обнаружения ошибки в комбинации а14. На рис. 2.4б показан случай перехода сигнала подтверждения на комбинацию
а22 в сигнал переспроса (Н). При этом передатчик, получив сигнал переспроса, искажает
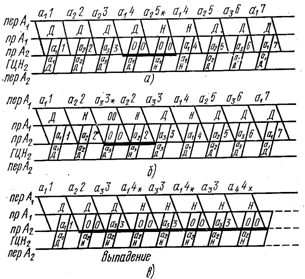
Рис. 2.4. Временные диаграммы работы системы с РОС-нпбл и циклической нумерацией сообщений
передаваемую в это время комбинацию а33. Получив трансформированный сигнал, передатчик по окончании передачи комбинации а33 повторяет комбинацию а22. Так как комбинация а33 преднамеренно искажена передатчиком, приемник обнаруживает эту ошибку и стирает комбинацию а33, давая сигнал на ее повторную передачу. Циклический номер а2 принятой затем комбинации а22 меньше ожидаемого номера а3, поэтому комбинации а22 также стирается, а по обратному каналу поступает сигнал подтверждения (Д), после чего передатчик повторяет комбинацию а33. При отсутствии цикловой нумерации в рассмотренной ситуации произошла бы вставка комбинации а22. На рис. 4б представлен случай, когда сигнал переспроса на комбинацию а22 перешел в сигнал подтверждения, что в случае отсутствия цикловой нумерации привело бы к выпадению этой комбинации. В рассматриваемом случае приемник одновременно с выдачей сигнала переспроса по комбинации а22 стирает комбинацию а33 и посылает на нее сигнал переспроса. Передатчик, получив этот сигнал, искажает комбинацию а14 и т. д„ т. е. система переходит в режим постоянного переспроса. Это фиксируется специальным устройством, и работа системы останавливается. Так удается избежать выпадения комбинаций. Поскольку большинство каналов связи является четырехпроходным, то с целью повышения их использования, кроме рассмотренных выше однонаправленных (симплексных или полудуплексных) СПДИ, широко применяются дуплексные СПДИ, в которых передача информации производится одновременно в двух направлениях. Это оказывается возможным благодаря тому, что переспросы в системе с РОС-нпбл происходят сравнительно редко и подавляющую часть времени обратный канал может быть использован для передачи.
Структурная схема дуплексной системы с -РОС-нпбп представлена на рис. 2.5. Сигналы решения.
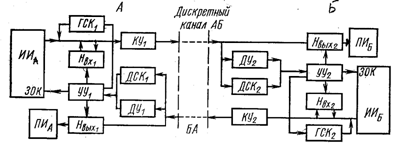
Рис. 2.5. Структурная схема дуплексной системы с РОС-нпбп
кодируются в виде комбинаций такой же длины, что и информационные комбинации, и передаются в обоих направлениях одновременно с информацией в общем потоке. Обмен информацией в такой системе при отсутствии ошибок в дискретных каналах АБ и БА происходит в обоих направлениях независимо в следующей последовательности. Передатчик станции А, запросив (сигнал ЗОК—запрос очередной комбинации) и получив информационную комбинацию от ИИа, вводит в нее избыточность (с помощью кодирующего устройства KУ1) и передает по дискретному каналу АБ на станцию Б. Приемник станции Б с помощью декодирующего устройства ДУ2 декодирует кодовую комбинацию и выдает ее ПИб. Одновременно по дискретному каналу БА аналогичным образом происходит передача информации от ИИб к ПИа. Такой режим функционирования системы (в условиях отсутствия ошибок) называют режимом работы. При наличии ошибок в дискретных каналах передача информации осуществляется в режиме переспроса. Информационные комбинации по запросу передатчика станции А от ИИа подаются на кодирующее устройство KУ1 и во входной накопитель Нвх1 рассчитанный на хранение М* последних информационных комбинаций, расположенных в той последовательности, в которой они должны выдаваться в дискретный канал. Закодированные помехоустойчивым кодом информационные комбинации по каналу АБ передаются через декодирующее устройство ДУ2 в выходной накопитель приемника станции Б Нвых2 и параллельно на дешифратор служебных комбинаций (сигнала переспроса) ДСК2. В тех случаях, когда ДУ2 обнаруживает ошибки в информационной комбинации или ДСК2 — сигнал переспроса, устройство управления УУ2 переводит приемник станции Б в режим переспроса. Аналогично работает приемник на станции А при передаче в обратном направлении и возникновении ошибки в канале БА. Случай возникновения ошибок одновременно в обоих каналах рассмотрен ниже.
Пусть, например, при передаче в направлении АБ искажена кодовая комбинация знака В (рис. 2.6а). После обнаружения ошибки в момент t1 ** по команде УУ2 приемник станции Б блокируется на М==5 циклов (стирает в Нвых2 пришедшую комбинацию и следующие М—1==4 комбинации), генератор служебных комбинаций ГСК2 выдает в обратный канал (БА) комбинацию запроса (КЗ), передатчик передает в канал БА М информационных комбинаций из Нвх2. При этом передатчик станции Б не выдает ИИб запросов на очередные информационные комбинации. Приемник станции А после получения комбинации запроса (момент t2) также блокируется на М=5 циклов и по сигналу ДСК. управляющее устройство дает команду ГСК1 на выдачу комбинации запроса, после передачи которой (момент t3) передатчик станции А повторно передает хранящиеся в Нвх1 М информационных комбинаций. В результате, как видно из диаграммы, в каналах обоих направлений передачи сохраняется нормальный порядок прохождения информации. Необходимость такого, на первый взгляд, переусложненного алгоритма, содержащего, казалось бы, лишние операции повторной передачи информации со станции Б и выдачи запроса со станции А, связана с возможностью искажения комбинации запроса.
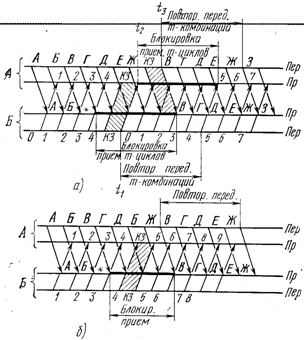
Рис. 2.6. Временные диаграммы работы дуплексной системы с РОС-нпвл при искажениях комбинаций в одном канале
Действительно, при безыскаженной передаче запросной комбинации алгоритм работы системы может быть упрощен: при приеме искаженного знака В станция Б блокирует приемник на М'==4 цикла и посылает комбинацию запроса, а информация не повторяется (рис. 2.6б). Станция А по получении сигнала запроса сразу же осуществляет повторную передачу. Однако в случае, когда запросная комбинация КЗ, посланная со станции Б, также искажается и воспринимается приемником станции А как искаженная информационная комбинация (рис. 2.6в), передатчик А посылает запрос на повторение этой комбинации и продолжает передачу следующей по порядку кодовой комбинации — знака 3. Однако, поскольку приемник станции Б после посылки запроса заблокировался на М=4 цикла, произойдет выпадение знаков В, Г, Д, Е, Ж. Для избежания такой ситуации используется более сложный алгоритм, временная диаграмма которого показана на рис. 2.6а.
Подобные системы часто называют системами с автоматическим запросом ошибок—АЗО. Эти системы используются в основном для передачи данных по каналам ТЧ. При применении модемов согласно рекомендации МККТТ V. 23 в канале ТЧ образуются два частотных подканала: прямой со скоростью передачи 1200 или 600 бит/с для передачи данных и обратный со скоростью 75 бит/с для передачи служебных комбинаций. В соответствии с рекомендацией МККТТ V 41 и ГОСТ кодовая комбинация содержит 240, 480 или 960 информационных единичных элементов, 16 проверочных единичных элементов, соответствующих порождающему многочлену х16+х12+х5+1, и четыре служебных единичных элемента. Для борьбы со вставками и выпадениями, возникающими по тем же причинам, которые были рассмотрены выше, применяют циклическую нумерацию вводимых в систему комбинаций с периодом h+1.
За данными:
Nopt=511 B=1200 V=80000 L=5500
За формулами:
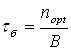 =0,426
=0,426
![]() =0,069
=0,069
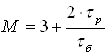 =3,323 ³ 4
=3,323 ³ 4
Временная диаграмма работы системы с РОС-нпбл представлена на Рис 2.7.
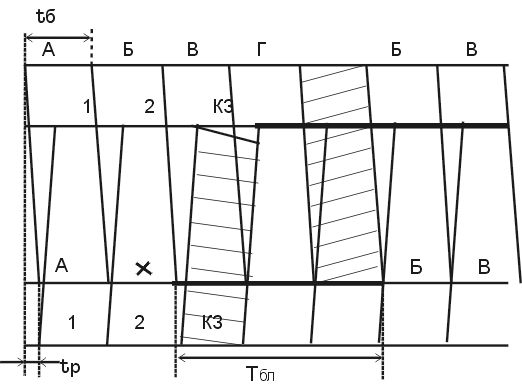
Рис. 2.7. Временные диаграммы работы дуплексной системы с РОС-нпвл.
3. Выбор оптимальной длины кодовой комбинации при использовании циклического кода в системе с РОС
Длина кодовой комбинации n должна быть выбрана таким образом, чтобы обеспечить наибольшую пропускную способность канала связи. При использовании корректирующего кода кодовая комбинация содержит n разрядов, из которых к разрядов являются информационными, а r разрядов - проверочными: n = k+r;
Если в системе связи используются двоичные сигналы (сигналы типа 1 и 0) и каждый единичный элемент несет не более одного бита информации, то между скоростью передачи информации и скоростью модуляции существует соотношение: C = k/n×B
где С - скорость передачи информации, бит/с,
В - скорость модуляции . Бод.
Очевидно, что чем меньше r, тем больше отношение k/n приближается к 1, тем меньше отличается С от В, т.е. тем выше пропускная способность системы связи.
Известно также, что для циклических кодов с минимальным кодовым расстоянием d0=3 справедливо соотношение:
r ³ log (n+1);
С точки зрения внесения постоянной избыточности в кодовую комбинацию выгодно выбирать длинные кодовые комбинации, так как с увеличением n относительная пропускная способность: R = C/B = k/n;
увеличивается, стремясь к пределу равному 1.
В реальных каналах связи действуют помехи, приводящие к появлению ошибок в кодовых комбинациях. При обнаружении ошибки декодирующим устройством в системах с РОС производится переспрос группы кодовых комбинаций. Во время переспроса полезная информация не передается, поэтому скорость передачи информации уменьшается.
В этом случае:
C = B k/n[1- Poo(M+1)/Pпп+Poo(M+1)]
где Pоо - вероятность обнаружения ошибки декодером (вероятность переспроса) ;
Рпп - вероятность правильного приема (безошибочного приема) кодовой комбинации;
М - емкость накопителя передатчика в числе кодовых комбинаций .
При малых вероятностях ошибки в канале связи (Рош<0.005) вероятность Роо также мала, поэтому знаменатель мало отличается от 1 и можно считать:
C»B×k/n[1-Poo(M+1)];
При независим ых ошибках в канале связи, при n ×Ро ш <<1
Poo» n×Poш;
тогда C» B×k/n[1-n×Poш(M+1)];
Емкость накопителя M= [3+2×tp/tкомб];
где tр-время распространения сигнала по каналу связи, с
tкомб - длительность кодовой комбинации из n разрядов , с
Но tp = L/v; tкомб = n/B;
После подстановок имеем R = k/n[1-Poш (4n+2LB/v)]; (1)
При наличии ошибок в канале связи величина R является функцией Рош, n, k, L, В, v. следовательно, существует оптимальное n при котором относительная пропускная способность будет максимальной.
Формула (1) еще более усложняется в случае зависимых ошибок в канале связи (при пакетировании ошибок).
Выведем эту формулу для модели ошибок Пуртова. Необходимо определить вероятность:
Р(³tоб,n ) = (n/ tоб) × Pош = (n/do-1) ×Pош
Рно»1/2 ×P(³tоб, n);
Подставляя значение заменой tоб на dо-1, имеем
r = {3.32[(1-a)×lg n/dо-1+lg Pош - lg Pно]} (2)
Окончательно
R = {1-3.32/n [(1-a)×lg n/d0-1+lg Pош - lg Pно]}× 1- Pош ×n (4+2LB/vn) (3)
К параметрам циклического кода относятся:
n- длина кодовой комбинации;
k- длина информационной части кодовой комбинации;
r- длина проверочной части кодовой комбинации;
Определим оптимальную длину кодовой комбинации n, обеспечивающую наибольшую относительную пропускную способность R и число проверочных разрядов r обеспечивающих заданную вероятность необнаруженной ошибки Рош при заданной кратности ошибок tоб внутри кодовой комбинации и заданной вероятности ошибок Рош в канале связи.
По результатам расчетов составляем таблицы для Рош = 0,0005 и Рош = 0,005:
L=5500 км; a=0.55; a0=4; V=80000 ; B=1200 Бод; Рно=3.0×10-6
n=2![]() -1
,где m=5...12
-1
,где m=5...12
R = {1-3.32/n [(1-a)×lg n/d0-1+lg Pош - lg Pно]}× 1- Pош ×n (4+2LB/vn)
r = {3.32[(1-a)×lg n/dо-1+lg Pош - lg Pно]}
k=n-r
Таблица 1 Рош = 0,0005
| R | n | r | k |
| 0.69758 | 31 | 9 | 22 |
| 0.83337 | 63 | 10 | 53 |
| 0.90115 | 127 | 10 | 117 |
| 0,93277 | 255 | 11 | 244 |
| 0.94402 | 511 | 11 | 500 |
| 0.94254 | 1023 | 12 | 1011 |
| 0.93163 | 2047 | 12 | 2035 |
| 0.91202 | 4095 | 13 | 4082 |
nопт=511
Из таблицы 1 видно, что наибольшую пропускную способность R=0.94402 обеспечивает циклический код с параметрами n= 511, r= 11. k=500
Таблица 1 Рош = 0,005
| R | n | r | k |
| 0.47359 | 31 | 13 | 18 |
| 0.62827 | 63 | 13 | 50 |
| 0.6865 | 127 | 14 | 113 |
| 0,68048 | 255 | 14 | 241 |
| 0.62465 | 511 | 15 | 496 |
| 0.52192 | 1023 | 15 | 1008 |
| 0.36679 | 2047 | 15 | 2032 |
| 0.14655 | 4095 | 16 | 4079 |
nопт=127
Из таблицы 2 видно, что наибольшую пропускную способность R= 0,6865 обеспечивает циклический код с параметрами n= 127, r= 14 k=113.
 |
Для полученой длинны блока построить граф розделения вероятности кратности ошибки.
Граф вероятностей P(t,n=n опт).
![]()
t£n/3
n=n оптимальный
n=511 P=0.0005
n=127 P=0.005