Курсовая работа: Разработка функциональной схемы конечного автомата
Елабужский Филиал Казанского Государственного Технического Университета им. А.Н. Туполева
Курсовая работа
по дисциплине:
"Схемотехника"
на тему:
"Разработка функциональной схемы конечного автомата"
Выполнила: студентка 3 курса
группы 22304 Шакирова Г.Р.
Проверила: Калганова Е.С.
Елабуга 2009
Содержание
Абстрактный синтез
Автомат Мили
Структурный синтез
Кодирование состояний автомата
Таблица кодирования входных сигналов
Таблица кодирования выходных сигналов
Таблица переходов и выходов абстрактного автомата
Абстрактный синтез
Товары стоимостью 3 и 7 рублей, принимаемые монеты достоинством 1 и 2 рубля.
1-й товар:
1+1+1
1+1+2 (сдача 1 руб.)
1+2
2+1
2+2 (сдача 1 руб.)
2-й товар:
1+1+1+1+1+1+1
2+1+1+1+1+1
1+2+1+1+1+1
1+1+2+1+1+1
1+1+1+2+1+1
1+1+1+1+2+1
1+1+1+1+1+2
2+2+1+1+1
2+1+2+1+1
2+1+1+2+1
2+1+1+1+2
1+2+2+1+1
1+1+2+2+1
1+1+1+2+2
1+2+1+2+1
2+2+2+1
1+2+2+2
2+1+2+2
2+2+1+2
2+2+2+2 (сдача 1 руб.)
1+1+1+1+1+1+2 (сдача 1 руб.)
1+1+1+2+1+2 (сдача 1 руб.)
1+1+2+1+1+2 (сдача 1 руб.)
1+2+1+1+1+2 (сдача 1 руб.)
2+1+1+1+1+2 (сдача 1 руб.)
1+1+1+1+2+2 (сдача 1 руб.)
X= (x1, x2, x3, x4) - множество входных сигналов
x1 - выбор 1-го товара
x2 - выбор 2-го товара
x3 - бросок 1 рубля в монетоприемник
x4 - бросок 2 рублей в монетоприемник
Y= (y0, y1, y2, y3; y4, y5) - множество выходных сигналов
y0 - ожидание выбора товара, щель монетоприемника закрыта
y1 - идет прием денег
y2 - выдача 2-го товара без сдачи
y3 - выдача 2-го товара со сдачей 1 руб.
y4 - выдача 1-го товара
y5 - выдача 1-го товара со сдачей 1 руб.
A= (a0, a1, a3, a4, a5, a6, a7, a8, a9, a10, a11, a12, a13, a14) - множество состояний
a0 - начальное состояние
a1 - выбран 1-ый товар, в автомате 0 руб.
a2 - выбран 1-ый товар, в автомате 1 руб.
a3 - выбран 1-ый товар, в автомате 2 руб.
a4 - выбран 1-ый товар, в автомате 3 руб. - выдача 1-го товара
a5 - выбран 1-ый товар, в автомате 4 руб. - выдача 1-го товара со сдачей 1 руб.
a6 - выбран 2-ой товар, в автомате 0 руб.
a7 - выбран 2-ой товар, в автомате 1 руб.
a8 - выбран 2-ой товар, в автомате 2 руб.
a9 - выбран 2-ой товар, в автомате 3 руб.
a10 - выбран 2-ой товар, в автомате 4 руб.
a11 - выбран 2-ой товар, в автомате 5 руб.
a12 - выбран 2-ой товар, в автомате 6 руб.
a13 - выбран 2-ой товар, в автомате 7 руб. - выдача 2-го товара
a14 - выбран 2-ой товар, в автомате 8 руб. - выдача 2-го товара со сдачей 1 руб.
Автомат Мили
Запишем алгоритм работы автомата Мили в табличном виде.
ai - состояния абстрактного автомата, xj - входные сигналы абстрактного автомата
| Таблица № 1 | |||||||||||||||
|
ai xj |
a0 | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 | a13 | a14 |
| x1 |
a1 y1 |
a1 y1 |
a2 y1 |
a3 y1 |
a0 y0 |
a0 y0 |
a6 y1 |
a7 y1 |
a8 y1 |
a9 y1 |
a10 y1 |
a11 y1 |
a12 y1 |
a0 y0 |
a0 y0 |
| x2 |
a2 y1 |
a1 y1 |
a2 y1 |
a3 y1 |
a0 y0 |
a0 y0 |
a6 y1 |
a7 y1 |
a8 y1 |
a9 y1 |
a10 y1 |
a11 y1 |
a12 y1 |
a0 y0 |
a0 y0 |
| x3 |
a0 y0 |
a2 y1 |
a3 y1 |
a4 y4 |
a0 y0 |
a0 y0 |
a7 y1 |
a8 y1 |
a9 y1 |
a10 y1 |
a11 y1 |
a12 y1 |
a13 y2 |
a0 y0 |
a0 y0 |
| x4 |
a0 y0 |
a3 y1 |
a4 y4 |
a5 y5 |
a0 y0 |
a0 y0 |
a8 y1 |
a9 y1 |
a10 y1 |
a11 y1 |
a12 y1 |
a13 y1 |
a14 y3 |
a0 y0 |
a0 y0 |
Запишем алгоритм работы автомата Мили, используя графический способ задания автомата.
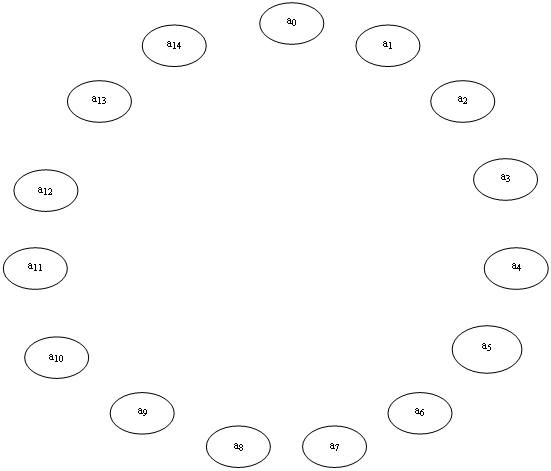
Рисунок № 1
Структурный синтез
R =] log215 [=4 - количество элементов памяти
L=] log24 [=2 - количество входных каналов
N=] log26 [=3 - количество выходных каналов
Синтез автомата Мили будем проводить на Т-триггерах.
Т-триггер (триггер со счетным входом) имеет один вход. Он "переворачивается", изменяя свое состояние, каждый раз, когда на его вход поступает сигнал, соответствующий логической единице.
При поступлении фронта импульса значение входного напряжения изменяет значение с уровня, равного логическому нулю, на значение, равное логической единице. При поступлении среза импульса значение входного напряжения изменяет значение с уровня, равного логической единице, на значение, равное уровню логического нуля.
Кодирование состояний автомата
Qk - состояния элементарного автомата, ai - состояния абстрактного автомата
| Таблица № 2 | ||||
|
Qk ai |
Q1 | Q2 | Q3 | Q4 |
| a0 | 0 | 0 | 0 | 0 |
| a1 | 0 | 0 | 0 | 1 |
| a2 | 0 | 0 | 1 | 0 |
| a3 | 0 | 0 | 1 | 1 |
| a4 | 0 | 1 | 0 | 0 |
| a5 | 0 | 1 | 0 | 1 |
| а6 | 0 | 1 | 1 | 0 |
| а7 | 0 | 1 | 1 | 1 |
| а8 | 1 | 0 | 0 | 0 |
| а9 | 1 | 0 | 0 | 1 |
| а10 | 1 | 0 | 1 | 0 |
| а11 | 1 | 0 | 1 | 1 |
| а12 | 1 | 1 | 0 | 0 |
| а13 | 1 | 1 | 0 | 1 |
| а14 | 1 | 1 | 1 | 0 |
Таблица кодирования входных сигналов
αm - входные сигналы структурного автомата, xj - входные сигналы абстрактного автомата
| Таблица № 3 | ||
|
αm xj |
α1 | α2 |
| x1 | 0 | 0 |
| x2 | 0 | 1 |
| x3 | 1 | 0 |
| x4 | 1 | 1 |
Таблица кодирования выходных сигналов
zp - выходные сигналы структурного автомата, ys - входные сигналы абстрактного автомата
| Таблица № 4 | |||
|
zp ys |
z1 | z2 | z3 |
| y0 | 0 | 0 | 0 |
| y1 | 0 | 0 | 1 |
| y2 | 0 | 1 | 0 |
| y3 | 0 | 1 | 1 |
| y4 | 1 | 0 | 0 |
| y5 | 1 | 0 | 1 |
Таблица переходов и выходов абстрактного автомата
ai - состояния абстрактного автомата, xj - входные сигналы абстрактного автомата
| Таблица № 5 | ||||||||
|
ai xj |
a0 0000 |
a1 0001 |
a2 0010 |
a3 0011 |
a4 0100 |
a5 0101 |
a6 0110 |
a7 0111 |
| 00 |
0001 001 |
0001 001 |
0010 001 |
0011 001 |
0000 000 |
0000 000 |
0110 001 |
0111 001 |
| 01 |
0010 001 |
0001 001 |
0010 001 |
0011 001 |
0000 000 |
0000 000 |
0110 001 |
0111 001 |
| 10 |
0000 000 |
0010 001 |
0011 001 |
0100 100 |
0000 000 |
0000 000 |
0111 001 |
1000 001 |
| 11 |
0000 000 |
0011 001 |
0100 100 |
0101 101 |
0000 000 |
0000 000 |
1000 001 |
1001 001 |
| Таблица № 5 (продолжение) | |||||||
|
ai αm |
a8 1000 |
a9 1001 |
a10 1010 |
a11 1011 |
a12 1100 |
a13 1101 |
a14 1110 |
| 00 |
1000 001 |
1001 001 |
1010 001 |
1011 001 |
1100 001 |
0000 000 |
0000 000 |
| 01 |
1000 001 |
1001 001 |
110 001 |
1011 001 |
1100 001 |
0000 000 |
0000 000 |
| 10 |
1001 001 |
1010 001 |
1011 001 |
1100 010 |
1101 010 |
0000 000 |
0000 000 |
| 11 |
1010 001 |
1011 001 |
1100 001 |
1101 001 |
1110 011 |
0000 000 |
0000 000 |
| Таблица № 6 | ||||||||||||||||
| α1 | α2 | Q1 | Q2 | Q3 | Q4 | Q1 (t+1) | Q2 (t+1) | Q3 (t+1) | Q4 (t+1) | z1 | z2 | z3 | T1 | T2 | T3 | T4 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | - | - | - | - | - | - | - | - | - | - | - |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 1 | 1 | - | - | - | - | - | - | - | - | - | - | - |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 | - | - | - | - | - | - | - | - | - | - | - |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 | - | - | - | - | - | - | - | - | - | - | - |
| Т1 Таблица № 7 | ||||||||||||||||
|
Qk αm |
0000 | 0001 | 0011 | 0010 | 0110 | 0111 | 0101 | 0100 | 1100 | 1101 | 1111 | 1110 | 1010 | 1011 | 1001 | 1000 |
| 00 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | - | 1 | 0 | 0 | 0 | 0 |
| 01 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | - | 1 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | - | 1 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | - | 1 | 0 | 0 | 0 | 0 |
| Т2 Таблица № 8 | ||||||||||||||||
|
Qk αm |
0000 | 0001 | 0011 | 0010 | 0110 | 0111 | 0101 | 0100 | 1100 | 1101 | 1111 | 1110 | 1010 | 1011 | 1001 | 1000 |
| 00 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | - | 1 | 0 | 0 | 0 | 0 |
| 01 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | - | 1 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | - | 1 | 1 | 1 | 0 | 0 |
| 10 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | - | 1 | 0 | 1 | 0 | 0 |
| Т3 Таблица № 9 | ||||||||||||||||
|
Qk αm |
0000 | 0001 | 0011 | 0010 | 0110 | 0111 | 0101 | 0100 | 1100 | 1101 | 1111 | 1110 | 1010 | 1011 | 1001 | 1000 |
| 00 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | - | 1 | 0 | 0 | 0 | 0 |
| 01 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | - | 1 | 0 | 0 | 0 | 0 |
| 11 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | - | 1 | 1 | 1 | 1 | 1 |
| 10 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | - | 1 | 0 | 1 | 1 | 0 |
| Т4 Таблица № 10 | ||||||||||||||||
|
Qk αm |
0000 | 0001 | 0011 | 0010 | 0110 | 0111 | 0101 | 0100 | 1100 | 1101 | 1111 | 1110 | 1010 | 1011 | 1001 | 1000 |
| 00 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | - | 0 | 0 | 0 | 0 | 0 |
| 01 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | - | 0 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | - | 0 | 0 | 0 | 0 | 0 |
| 10 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | - | 0 | 1 | 1 | 1 | 1 |
| Z1 Таблица № 11 | ||||||||||||||||
|
Qk αm |
0000 | 0001 | 0011 | 0010 | 0110 | 0111 | 0101 | 0100 | 1100 | 1101 | 1111 | 1110 | 1010 | 1011 | 1001 | 1000 |
| 00 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | - | 0 | 0 | 0 | 0 | 0 |
| 01 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | - | 0 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | - | 0 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | - | 0 | 0 | 0 | 0 | 0 |
| Z2 Таблица № 12 | ||||||||||||||||
|
Qk αm |
0000 | 0001 | 0011 | 0010 | 0110 | 0111 | 0101 | 0100 | 1100 | 1101 | 1111 | 1110 | 1010 | 1011 | 1001 | 1000 |
| 00 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | - | 0 | 0 | 0 | 0 | 0 |
| 01 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | - | 0 | 0 | 0 | 0 | 0 |
| 11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | - | 0 | 0 | 0 | 0 | 0 |
| 10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | - | 0 | 0 | 0 | 0 | 0 |
| Z3 Таблица № 13 | ||||||||||||||||
|
Qk αm |
0000 | 0001 | 0011 | 0010 | 0110 | 0111 | 0101 | 0100 | 1100 | 1101 | 1111 | 1110 | 1010 | 1011 | 1001 | 1000 |
| 00 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | - | 0 | 1 | 1 | 1 | 1 |
| 01 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | - | 0 | 1 | 1 | 1 | 0 |
| 11 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | - | 0 | 1 | 1 | 1 | 1 |
| 10 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | - | 0 | 1 | 1 | 1 | 1 |
Записываем выражения для функции возбуждения и выходов.
T1=α1 α2Q1Q2Q3+ α1Q1Q2Q3Q4+Q1Q2Q4+Q1Q2Q3=
=Q2 (α1Q1 (Q3 (α2+Q4)) +Q1 (Q4+Q3))
T2= α1Q1Q2Q3Q4+ α1 α2 Q1Q3+ +α1Q1Q2Q4+Q1Q2Q3+Q1Q2Q4+Q1Q2Q3+ α1 α2Q1Q3+
+α1 Q1Q2Q3Q4=
=α1 Q3 (α2+Q2Q4) +Q2
T3= α1 α2Q1Q2Q3Q4+ α1Q1Q2Q4+ α1 α2Q1+ +α1Q1Q2Q3Q4+ α1 α2Q1Q2Q3Q4+Q1Q2Q3+ α1 α2Q1Q2+ +α1Q1Q2Q4=
=α1Q1 (α2+Q2Q3Q4) + α2Q3Q4+Q1 (α1Q2 (α2+Q4) +Q2Q3)
T4= α1 α2Q1Q2Q3Q4+ α1 α2Q1+ α1 α2Q1+Q1Q2Q3Q4+ +α1 α2Q1Q2Q3+Q1Q2Q4+ α1 α2Q1Q2=
= α1 α2Q1 (Q2Q3+Q2) + α2Q1 ( α1Q2Q3Q4+ +α1) +Q2Q4 (Q1Q3+Q1)
z1= α1Q1Q2Q3Q4+ α1 α2Q1Q2Q3=
= α1Q1Q2 (Q3 (Q4+ α2))
z2= α1Q1Q2Q2Q4
z3= α1Q1Q2+ α2Q1Q2Q4+ α1 α2Q1Q3Q4+Q1Q2Q3+
+ α1Q1Q2Q3Q4+ α2Q1Q2Q3Q4=
=Q1Q2Q3Q4 ( α1+α2) + Q1 (Q2 ( α1+ α2Q4)) +Q3 (α1 α2Q4+Q2)