Курсовая работа: Теория автоматического управления
Запишем передаточную функцию разомкнутой системы:
![]() . (1)
. (1)
Передаточная функция замкнутой системы имеет вид:
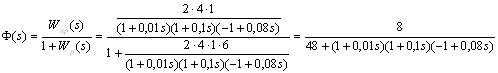 .
.
Характеристическое уравнение замкнутой системы:
![]() (2)
(2)
Корни характеристического уравнения (2):
![]()
Характеристическое уравнение (2) имеет два правых корня, следовательно, данная замкнутая система неустойчива.
1.2 Анализ устойчивости системы по алгебраическому критерию
Для характеристического уравнения (2) замкнутой системы коэффициенты ai, i=0..3,
а0=0.00008,
a1=0.0078,
a2= – 0.03,
a3=48.
Необходимым условием устойчивости системы является:
ai>0, i=0..3
Данное условие не выполняется (a2<0), следовательно, замкнутая система неустойчива.
1.3 Анализ устойчивости системы по частотным критериям
а) Критерий Найквиста (на комплексной плоскости)
Используя передаточную функцию разомкнутой системы (1) запишем характеристическое уравнение разомкнутой системы:
![]() . (3)
. (3)
Найдем корни характеристического уравнения (3):
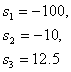
Характеристическое уравнение разомкнутой системы (3) имеет один правый корень, следовательно, разомкнутая система неустойчива.
Построим годограф Найквиста. Для этого определим частотную передаточную функцию разомкнутой системы и ее действительную и мнимую части.
 (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
Используя выражения (5) и (6), заполним таблицу:
Таблица 1.3.1
|
w |
0 | - | - | ∞ |
|
P |
-48 | 0 | - | 0 |
|
Q |
0 | - | 0 | 0 |
Построим годограф Найквиста (Рис. 1.3.1):
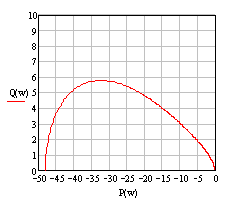
Рис. 1.3.1
Для случая,
когда разомкнутая система неустойчива критерий Найквиста звучит следующим
образом: для устойчивости замкнутой системы необходимо и достаточно, чтобы
годограф Найквиста охватывал особую точку (![]() ;
;
![]() ) в положительном
направлении на угол
) в положительном
направлении на угол ![]() , где l – число правых корней
характеристического уравнения разомкнутой системы.
, где l – число правых корней
характеристического уравнения разомкнутой системы.
Число правых корней характеристического уравнения разомкнутой системы (3) равно единице (l=1), полученный годограф не охватывает особую точку (-1, j0) на угол lπ=π (годограф охватывает особую точку в направлении по часовой стрелке), следовательно, критерий Найквиста не выполняется и система неустойчива.
б) Критерий Найквиста (на плоскости ЛЧХ)
Построим ЛЧХ заданной системы, для этого определим расчетные выражения для L(w) и φ(w):
![]() (7)
(7)
![]() (8)
(8)
Для построения асимптотической ЛАЧХ найдем параметры:
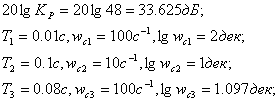
ЛФЧХ системы также можно построить как геометрическую сумму ЛФЧХ отдельных звеньев системы.
Графики расчетных ЛЧХ, построенные по формулам (7) и (8) изображены на рисунке (1.3.2):
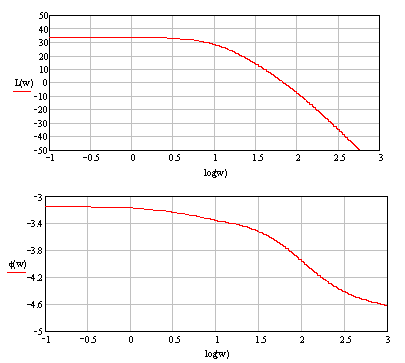
Рис. 1.3.2
wср(частота среза) – частота, соответствующая пересечению ЛАЧХ с осью lgw;
wкр(критическая частота) – частота, соответствующая пересечению ЛФЧХ уровня –π;
Система устойчива, если выполняется условие:
wср< wкр
Данное условие не выполняется, следовательно, система неустойчива. Аналогичный вывод можно сделать по асимптотической ЛАЧХ и ЛФЧХ системы, построенной как сумма отдельных звеньев, входящих в систему, изображенной на рисунке (1.3.3):
в) Критерий Михайлова
Используя характеристическое уравнение замкнутой системы (2) введем функцию Михайлова:
![]() , где
, где
![]() ,
,
![]() .
.
Для заданной системы функция Михайлова примет вид:
![]()
![]() (9)
(9)
![]() (10)
(10)
Графическое
изображение функции Михайлова на комплексной плоскости при ![]() называется годографом
Михайлова. Для устойчивости системы n-го порядка необходимо и достаточно, чтобы
годограф Михайлова начинался на вещественной положительной полуоси и при
увеличении частоты до ∞ проходил последовательно в положительном
направлении n
квадрантов, нигде не обращаясь в ноль.
называется годографом
Михайлова. Для устойчивости системы n-го порядка необходимо и достаточно, чтобы
годограф Михайлова начинался на вещественной положительной полуоси и при
увеличении частоты до ∞ проходил последовательно в положительном
направлении n
квадрантов, нигде не обращаясь в ноль.
Используя выражения (9) и (10), заполним таблицу:
Таблица 1.3.3
|
w |
0 | 77,625 | - | ∞ |
|
X(w) |
47 | 0 | - | -∞ |
|
Y(w) |
0 | -39,748 | 0 | -∞ |
Построим годограф Михайлова (Рис. 1.3.4):
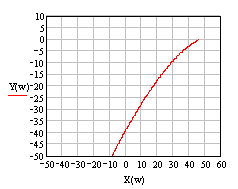
Рис. 1.3.4
Полученный годограф начинается на вещественной положительной полуоси, проходит 2 квадранта в отрицательном направлении, таким образом, критерий Михайлова не выполняется, следовательно, система неустойчива.
2. Построение области устойчивости в плоскости параметра Кр
Построим область устойчивости, используя критерий Гурвица.
Запишем характеристическое уравнение замкнутой системы в общем виде:
![]() .
.
![]()
![]()
Для конкретного случая характеристическое уравнение замкнутой системы имеет вид:
![]() (11)
(11)
Для устойчивости системы КР должно удовлетворять необходимому условию
![]()
![]()
Рис. 2.1
Но заметим, что исходный КР удовлетворяет этому условию, и его изменением устойчивости замкнутой системы добиться невозможно, т. к. в ХУ ЗС (2.3) а2<0, и зависит этот коэффициент от постоянных времени.
Построим область устойчивости в плоскости параметра Т2
Необходимое условие устойчивости:
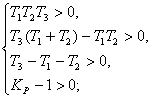
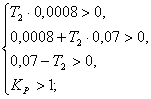
Достаточное условие устойчивости для системы третьего порядка по критерию Гурвица имеет вид:
![]()
![]()
![]()
![]()
![]()
Учитывая все условия:
![]()
![]()
Рис. 2.2
3. Коррекция системы
Для обеспечения устойчивости системы необходимо ввести корректирующее звено с передаточной функцией вида:
![]()
Структурная схема скорректированной системы (Рис. 3.1):
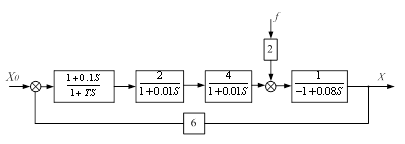
Рис. 3.1
Передаточная функция скорректированной разомкнутой системы имеет вид:
![]() (12)
(12)
Определим параметр Т из условия обеспечения минимального запаса устойчивости (Lзап=5 дБ).
Запас по амплитуде определяется на критической частоте – частоте, на которой функция φ(w) принимает значение, равное -π
Расчетное выражение для φ(w):
![]()
![]() , отсюда
, отсюда
![]() (13)
(13)
Расчетное выражение для L(w):
![]() (14)
(14)
Подставим найденное выражение Т (13) в функцию L(w) (14):
![]()
На критической частоте значение функции L(w), исходя из условия обеспечения минимального запаса устойчивости, должно быть равно не менее 5 дБ.
![]()
Из данного выражения найдем wкр
wкр=308,4185, следовательно,
Т=0,001198
Анализируя
данное значение и область устойчивости, найденную в п. 2, можно сделать
вывод, что введение корректирующего звена с передаточной функцией ![]() обеспечит не только
устойчивость системы, но и более чем минимальный запас устойчивости по
амплитуде.
обеспечит не только
устойчивость системы, но и более чем минимальный запас устойчивости по
амплитуде.
4. Построение и анализ ЛЧХ системы и годографа Найквиста скорректированной системы
Используя передаточную функцию скорректированной разомкнутой системы (12), запишем характеристическое уравнение скорректированной разомкнутой системы:
![]() (15)
(15)
Найдем корни характеристического уравнения (15):
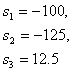
Уравнение (15) имеет один правый корень, следовательно, скорректированная разомкнутая система неустойчива.
Построим годограф Найквиста. Для этого определим частотную передаточную функцию скорректированной разомкнутой системы и ее действительную и мнимую части.

![]() (16)
(16)
![]() (17)
(17)
Используя выражения (16) и (17), заполним таблицу:
Таблица 4.1
|
w |
0 | - | 328,8237 | ∞ |
|
P |
-48 | 0 | -0,485 | 0 |
|
Q |
0 | - | 0 | 0 |
Построим годограф Найквиста (Рис. 4.1):
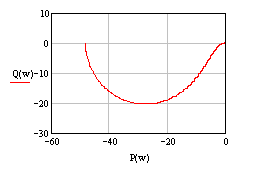
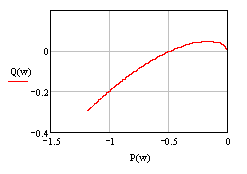
Рис. 4.1
Для случая,
когда разомкнутая система неустойчива критерий Найквиста звучит следующим
образом: для устойчивости замкнутой системы необходимо и достаточно, чтобы
годограф Найквиста охватывал особую точку (![]() ;
;
![]() ) в положительном
направлении на угол
) в положительном
направлении на угол ![]() , где l – число правых корней характеристического
уравнения разомкнутой системы.
, где l – число правых корней характеристического
уравнения разомкнутой системы.
Число правых корней характеристического уравнения разомкнутой системы равно единице (l=1), полученный годограф охватывает особую точку (-1, j0) на угол lπ=π, следовательно, критерий Найквиста выполняется и система устойчива.
Построим ЛЧХ разомкнутой скорректированной системы:
Определим расчетные выражения для L(w) и φ(w):
![]() (18)
(18)
![]() (19)
(19)
Для построения асимптотической ЛАЧХ найдем параметры:
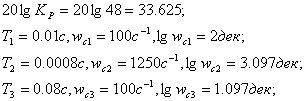
ЛФЧХ системы также можно построить как геометрическую сумму ЛФЧХ отдельных звеньев системы.
Графики расчетных ЛЧХ, построенные по формулам (18) и (19), изображены на рисунке (4.2):
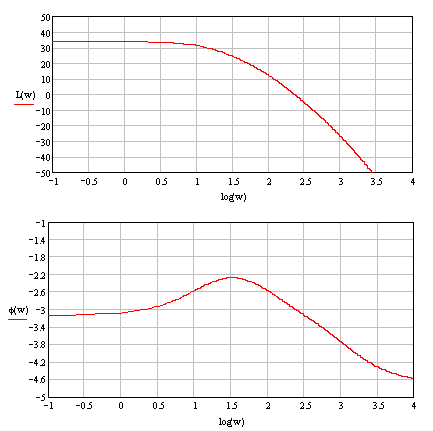
Рис. 4.2
wср(частота среза) – частота, соответствующая пересечению ЛАЧХ с осью lgw;
wкр(критическая частота) – частота, соответствующая пересечению ЛФЧХ уровня –π;
Система устойчива, если выполняется условие:
wср< wкр
Данное условие выполняется, следовательно, система устойчива. Запас устойчивости по амплитуде: Lзап= 5,8 дБ
Запас устойчивости по фазе: φзап=0,2 рад
Аналогичный вывод можно сделать по асимптотической ЛАЧХ и ЛФЧХ системы, построенной как сумма отдельных звеньев, входящих в систему.
5. Анализ качества системы в переходном режиме
Определим прямые показатели качества, для этого построим переходную характеристику:
![]() , где (20)
, где (20)
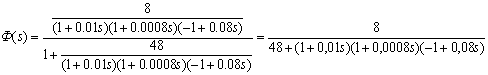 (21)
(21)
Ф(s) – передаточная функция скорректированной замкнутой системы.
Переходная характеристика, построенная по формуле (20), изображена на рисунке (5.1):
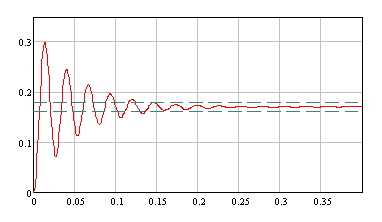
Рис. 5.1
По рисунку (5.1) определим: hmax=0.3; hуст=0.17; h(0)=0, время регулирования на уровне 0.05 (hуст-h(0)).
Коридор: [0.95 (hуст-h(0)); 1.05 (hуст-h(0))].
Коридор: [0.1615; 0.1785].
Время регулирования: tрег= 0,15 с.
Перерегулирование равно:
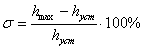 (5.3)
(5.3)
![]() .
.
Определим показатель коллебательности. Используя передаточную функцию скорректированной замкнутой системы (21), запишем частотную передаточную функцию скорректированной замкнутой системы:

Выделим действительную и мнимую части:
![]()
![]()
Модуль частотной передаточной функции замкнутой системы:
![]() (22)
(22)
Построим амплитудно-частотную характеристику, используя выражение (22) (Рис. 5.2):
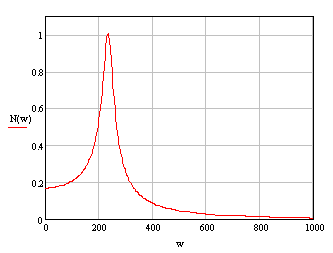
Рис. 5.2
По рисунку
(5.2) определим: ![]() ;
; ![]() .
.
Показатель колебательности M есть отношение максимальной ординаты амплитудно-частотной характеристики замкнутой системы к начальной ординате:
![]()
![]()
Определим запасы устойчивости системы.
Найдем критическую частоту – частоту, на которой значение φ(w) равняется –π.
![]() (23)
(23)
![]()
wкр=328,824
Рассчитаем запас по амплитуде:
![]() (24)
(24)
![]()
Запас по амплитуде: Lзап= 5,797 дБ
Найдем частоту среза – частоту, на которой значение L(w) равняется 0, используя выражение (24):
![]()
wср=232,624
Рассчитаем запас по фазе, используя выражение (23):
![]()
Запас по фазе: φзап=0,168 рад.
6. Анализ качества системы в установившемся режиме
Установившаяся ошибка системы равна:
![]() (25)
(25)
εустХо=С0Х0(t)+ С1Х'0(t)+…
εуст f =С0F0(t)+ С1F'0(t)+…
Так как в заданном случае задающее и возмущающее воздействия – константы, необходимо найти лишь первые коэффициенты функций ошибок.
Запишем передаточную функцию замкнутой системы по ошибке по задающему воздействию:
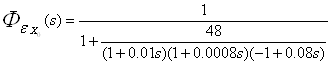
![]()
Установившаяся ошибка системы по задающему воздействию:
![]()
Запишем передаточную функцию замкнутой системы по ошибке по возмущению:
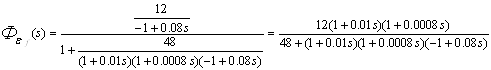
![]()
Установившаяся ошибка системы по задающему воздействию:
![]()
Рассчитаем установившуюся ошибку системы, используя выражение (25):
![]()
Приведем размерность установившейся ошибки к размерности входного сигнала:
![]() ;
;
![]()
Система является статической как относительно возмущения, так и относительно задающего воздействия, установившаяся ошибка системы равна 7/282.