Курсовая работа: Уравнения равновесия
Министерство образования РБ
Учреждение образования
« Гомельский Государственный
университет имени Ф. Скорины »
Математический факультет
Кафедра дифференциальных уравнений
Курсовая работа
«Уравнения равновесия»
Исполнитель:
Студентка группы М-41 ____________ Поляк Е. М.
Научный руководитель:
Кандидат физико-математических наук
____________ Вересович П.П.
Гомель 2006
Содержание
Введение 3
Постановка задачи 4
Уравнения равновесия 5
Решение уравнений равновесия 12
Заключение 16
Список использованной литературы 17
Введение
Актуальным направлением научно-технического прогресса является развитие и широкое использование возможностей современных высокопроизводительных компьютеров, сетей мультипрограммных ЭВМ и на этой основе - применение математических методов моделирования в научных исследованиях. Развитие вычислительной техники в Республике Беларусь приводит к необходимости создания систем и сетей ЭВМ, эффективно обслуживающих запросы различных пользователей. Благодоря задачам, связанным с математическим моделированием мультипрограммных вычислительных систем и анализом их производительности, с проектированием и анализом сетей передачи данных и сетей ЭВМ теория сетей массового обслуживания (СМО) является сравнительно новым и быстро развивающимся разделом теории массового обслуживания.
Исходным материалом для аналитического исследования СМО является стационарное (инвариантное) распределение вероятностей состояний. Ввиду сложности и многомерности случайных процессов, описывающих функционирование таких сетей, большинство аналитических результатов связано с получением стационарного распределения в форме произведения множителей, характеризующих стационарное распределение отдельных узлов сети.
Актуальным вопросом, связанным с исследованием СМО является доказательство инвариатности стационарного распределения таких сетей относительно функционального вида распределений длительности обслуживания в узлах, позволяющее при проектировании и эксплуатации реальных сетей, считать, что обслуживание в узлах имеет наиболее простое для анализа распределение - экспоненциальное.
Постановка задачи
Сеть
состоит из двух приборов, на каждый из которых поступает простейший поток с
параметрами ![]() и
и ![]() соответственно. В случае,
если прибор занят, заявка, поступающая на него выбивает заявку находящуюся на
приборе, и та становится в очередь на дообслуживание. После обслуживания на I
приборе заявка с вероятностью
соответственно. В случае,
если прибор занят, заявка, поступающая на него выбивает заявку находящуюся на
приборе, и та становится в очередь на дообслуживание. После обслуживания на I
приборе заявка с вероятностью ![]() уходит
из сети, а с вероятностью
уходит
из сети, а с вероятностью ![]() поступает
на II прибор. Аналогично, после обслуживания на II приборе заявка с
вероятностью
поступает
на II прибор. Аналогично, после обслуживания на II приборе заявка с
вероятностью ![]() уходит из сети, а с
вероятностью
уходит из сети, а с
вероятностью ![]() поступает на I прибор.
поступает на I прибор.
Пусть
![]() - число заявок в очереди
на I приборе,
- число заявок в очереди
на I приборе, ![]() - число заявок в
очереди на II приборе,
- число заявок в
очереди на II приборе, ![]() - функция
распределения времени обслуживания
- функция
распределения времени обслуживания ![]() -ой
заявки на I приборе,
-ой
заявки на I приборе, ![]() - функция
распределения времени обслуживания
- функция
распределения времени обслуживания ![]() -ой
заявки на II приборе. Предполагается, что
-ой
заявки на II приборе. Предполагается, что
 =
= 
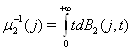 =
= 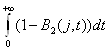
Требуется
доказать, что стационарное распределение ![]() не
зависит от вида функций распределения времени обслуживания
не
зависит от вида функций распределения времени обслуживания ![]() . При этом можно считать,
что
. При этом можно считать,
что
 ,
,
где
![]() ,
, ![]() ,
,
т.е.
когда ![]() - экспоненциальны.
- экспоненциальны.
Уравнения равновесия
Введем случайный процесс
![]() ,
,
где
![]() - число заявок в очереди
на I приборе в момент времени
- число заявок в очереди
на I приборе в момент времени ![]() ,
, ![]() - число заявок в очереди
на II приборе в момент времени
- число заявок в очереди
на II приборе в момент времени ![]() ,
, ![]() -время, которое еще будет
дообслуживаться заявка с момента
-время, которое еще будет
дообслуживаться заявка с момента ![]() , стоящая
i-ой в очереди I прибора,
, стоящая
i-ой в очереди I прибора, ![]() -время,
которое еще будет дообслуживаться заявка с момента
-время,
которое еще будет дообслуживаться заявка с момента ![]() ,
стоящая j-ой в очереди II прибора.
,
стоящая j-ой в очереди II прибора.
Пусть
существует стационарное эргодическое распределение процесса ![]() и процесса
и процесса ![]() , т.к. процесс
, т.к. процесс ![]() - это процесс
- это процесс ![]() , дополненный непрерывными
компонентами до того, чтобы быть марковским.
, дополненный непрерывными
компонентами до того, чтобы быть марковским.
Изучим
поведение процесса ![]() в устойчивом
режиме. Пусть
в устойчивом
режиме. Пусть
![]()
Введем в рассмотрение событие А, состоящее в том, что
![]()
![]()
а)
Предположим, что за время от ![]() до
до ![]() не было поступления
требований. Тому, чтобы
не было поступления
требований. Тому, чтобы ![]() не
изменило за время
не
изменило за время ![]() своего значения
и при этом выполнилось событие А, отвечает выражение:
своего значения
и при этом выполнилось событие А, отвечает выражение:
![]()
![]()
б)
Тому, что за время от ![]() до
до ![]() на 1-ом приборе обслужена
заявка и ушла из сети, отвечает слагаемое:
на 1-ом приборе обслужена
заявка и ушла из сети, отвечает слагаемое:
![]()
![]()
Тому,
что за время от ![]() до
до ![]() на 2-ом приборе обслужена
заявка и ушла из сети, отвечает слагаемое:
на 2-ом приборе обслужена
заявка и ушла из сети, отвечает слагаемое:
![]()
![]()
в)
Тому, что за время от ![]() до
до ![]() на 1-ый прибор поступила
заявка. Количество времени на дообслуживание этой заявки должно быть не больше,
чем
на 1-ый прибор поступила
заявка. Количество времени на дообслуживание этой заявки должно быть не больше,
чем ![]() , где
, где ![]() - определяется моментом
поступления заявки внутри интервала
- определяется моментом
поступления заявки внутри интервала ![]() . Этому
случаю отвечает слагаемое:
. Этому
случаю отвечает слагаемое:
![]()
![]()
![]()
Тому,
что за время от ![]() до
до ![]() на 2-ой прибор поступила
заявка. Количество времени на дообслуживание этой заявки должно быть не больше,
чем
на 2-ой прибор поступила
заявка. Количество времени на дообслуживание этой заявки должно быть не больше,
чем ![]() , где
, где ![]() - определяется моментом
поступления заявки внутри интервала
- определяется моментом
поступления заявки внутри интервала ![]() . Этому
случаю отвечает слагаемое:
. Этому
случаю отвечает слагаемое:
![]()
![]()
![]()
г)
Если в интервале ![]() заявка окончила
свое обслуживание на I приборе и перешла на II, то время на ее дообслуживание
II прибором должно быть не больше, чем
заявка окончила
свое обслуживание на I приборе и перешла на II, то время на ее дообслуживание
II прибором должно быть не больше, чем ![]() ,
где
,
где ![]() - определяется моментом
поступления заявки внутри интервала
- определяется моментом
поступления заявки внутри интервала ![]() .
.
![]()
![]()
![]()
Если
в интервале ![]() заявка окончила свое
обслуживание на II приборе и перешла на I, то время на ее дообслуживание I
прибором должно быть не больше, чем
заявка окончила свое
обслуживание на II приборе и перешла на I, то время на ее дообслуживание I
прибором должно быть не больше, чем ![]() , где
, где ![]() - определяется моментом
поступления заявки внутри интервала
- определяется моментом
поступления заявки внутри интервала ![]() .
.
![]()
![]()
![]()
Наконец,
остальные случаи, благодаря событию А сводятся к тому, что за время ![]() либо поступало, либо
обслужено более одной заявки, или заявки поступали и обслуживались. Для
простейшего входящего потока вероятность поступления двух и более заявок за
время
либо поступало, либо
обслужено более одной заявки, или заявки поступали и обслуживались. Для
простейшего входящего потока вероятность поступления двух и более заявок за
время ![]() есть
есть ![]() . Если же мы будем
рассматривать слагаемые, соответствующие возможности окончания обслуживания в
сочетании с поступлением заявок, то, очевидно, что эти слагаемые есть
. Если же мы будем
рассматривать слагаемые, соответствующие возможности окончания обслуживания в
сочетании с поступлением заявок, то, очевидно, что эти слагаемые есть ![]() . Таким образом, приходим к
следующим соотношениям:
. Таким образом, приходим к
следующим соотношениям:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Вводя обозначение
![]()
![]()
и учитывая, что
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
последнее соотношение перепишется в виде
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рассматривая
все слагаемые в последнем соотношении как сложные функции от ![]() , разлагаем их в ряд
Тейлора в окрестности 0 с остаточным членом в форме Пеано:
, разлагаем их в ряд
Тейлора в окрестности 0 с остаточным членом в форме Пеано:
![]()
![]()
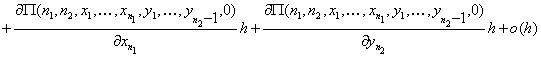 .
.
После
чего приводим подобные слагаемые и устремляем ![]() к
к
![]() . Тогда вводя обозначение
. Тогда вводя обозначение
![]()
и учитывая, что
![]() ,
,
![]() ,
,
![]() ,
,
получаем,
что свободные члены сократились, а слагаемые, содержащие своим сомножителем ![]() образуют уравнениям
равновесия.
образуют уравнениям
равновесия.
Таким образом, приходим к уравнениям равновесия:
![]()
![]()
![]()
![]()
![]()
![]()
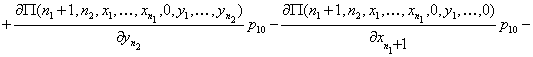
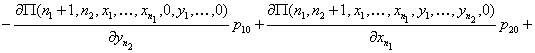
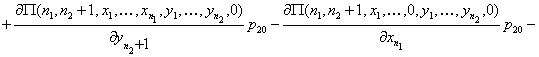
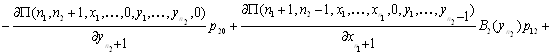
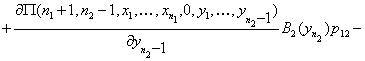
![]()
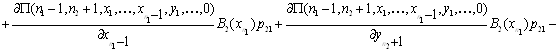
![]() .
.
Решение уравнений равновесия
Покажем,
что ![]() удовлетворяет нашим
уравнениям равновесия, где
удовлетворяет нашим
уравнениям равновесия, где ![]() - решение
для случая, когда
- решение
для случая, когда ![]() и
и ![]() - экспоненциальны, т.е.
- экспоненциальны, т.е.
 ,
,
 .
.
Для
этого распишем все частные производные функции ![]() .
.

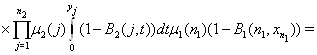
![]()
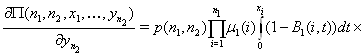

![]() .
.
С
учетом вида функции ![]() уравнения
равновесия перепишутся в виде
уравнения
равновесия перепишутся в виде
![]()
![]()
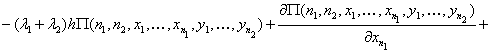
![]()
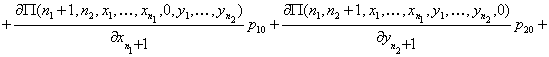
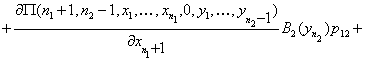
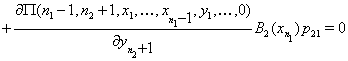 .
.
Подставив
![]() в это уравнение и,
учитывая, что
в это уравнение и,
учитывая, что
![]()
![]()
![]()
приходим к выводу, что функция
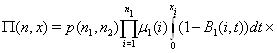
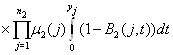 .
.
есть неотрицательное, абсолютно-непрерывное решение исходных уравнений равновесия.
Отсюда
следует, что стационарное распределение ![]() не
зависит от вида функций распределения времени обслуживания
не
зависит от вида функций распределения времени обслуживания ![]() и
и ![]() , поскольку
, поскольку ![]() , при этом можно считать,
что
, при этом можно считать,
что
 ,
,
где
![]() ,
, ![]() ,
,
т.е.
когда ![]() и
и ![]() - экспоненциальны.
- экспоненциальны.
Заключение
Таким
образом, для рассматриваемой сети массового обслуживания установлена инвариантность
стационарного распределения относительно функционального вида распределений
длительности обслуживания в узлах, т.е. установили, что стационарное
распределение ![]() не зависит от
вида функций распределения времени обслуживания
не зависит от
вида функций распределения времени обслуживания ![]() и
и
![]() , если известно, что для
них выполняется следующие ограничения:
, если известно, что для
них выполняется следующие ограничения:
 =
= 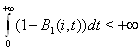
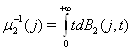 =
= 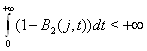
При
этом, можно считать, что функции распределения времени обслуживания ![]() и
и ![]() имеют экспоненциальный
вид.
имеют экспоненциальный
вид.
Список использованной литературы
1. Буриков А.Д., Малинковский Ю.В., Маталыцкий М.А.//Теория массового обслуживания: Учебное пособие по спецкурсу.-Гродно: 1984г.-108с.
2. Гнеденко Б.В., Коваленко И.Н. // Введение в теорию массового обслуживания.-Москва: Наука. 1966г.-432с.
| Лекции по твердотельной электронике | |
|
Московский энергетический институт (технический университет) ТВЕРДОТЕЛЬНАЯ ЭЛЕКТРОНИКА Конспект лекций Москва, 2002 г. Содержание Лекция 1 5 1 ... При приложении к переходу (диоду) обратного смещения U<0 концентрация неосновных носителей экспоненциально уменьшается, поскольку из соседней области носители перестают поступать ... Обозначим 1/(1+ѭѭp) как Ѭ2p, диффузионную длину зависящую от частоты, тогда уравнение (4_106) примет такой же вид как решенное нами ранее для транзистора стационарное уравнение: |
Раздел: Рефераты по радиоэлектронике Тип: реферат |
| Оборудование летательных аппаратов | |
|
Практическая работа N12-6 СИСТЕМА ВОЗДУШНЫХ СИГНАЛОВ СВС-72-3 (Продолжительность практической работы - 4 часа) I. ЦЕЛЬ РАБОТЫ Целью работы ячвляется ... 1-ой скорости 1мм/с соответствует интервал, который у Прибор питается U постоянного тока 27В, которое поступает на ста- |
Раздел: Рефераты по авиации и космонавтике Тип: реферат |
| Разработка и исследование имитационной модели разветвленной СМО ... | |
|
Аннотация к работе "Разработка и исследование имитационной модели разветвленной СМО (системы массового обслуживания) в среде VB5" Работа посвящена ... На вход системы из N станций поступает поток заявок с заданным законом распределения времени прихода (экспоненциальным или нормальным). Для простейшего потока с интенсивностью l интервал между соседними событиями имеет так называемое экспоненциальное распределение с плотностью |
Раздел: Рефераты по радиоэлектронике Тип: реферат |
| Моделирование систем массового обслуживания | |
|
Содержание ВВЕДЕНИЕ ГЛАВА I. ПОСТАНОВКА ЗАДАЧ МАССОВОГО ОБСЛУЖИВАНИЯ 1.1 Общие понятие теории массового обслуживания 1.2 Моделирование систем ... Для такого потока заявок время между двумя соседними заявками Т распределено экспоненциально с плотностью вероятности: Поскольку предельные вероятности системы постоянны, то заменив в уравнениях Колмогорова соответствующие производные нулевыми значениями, получим систему линейных алгебраических ... |
Раздел: Рефераты по экономико-математическому моделированию Тип: курсовая работа |
| Владимира Иннокентьевича Бабецкого (3 семестр) | |
|
Лекции по физике Владимира Иннокентьевича Бабецкого (III семестр физики на факультете "Прикладная математика и физика" МАИ) 2000г. §1. Введение Вот то ... Когда устанавливается равновесие, излучаемая площадкой энергия в заданном интервале должна равняться поглощаемой энергии в данном интервале (иначе эта площадка либо охлаждалась бы ... Как теория эту проблему решила, мы уже сейчас знаем: в стационарных состояниях пространственная конфигурация не меняется, она застывшая (это было видно из решения уравнения ... |
Раздел: Рефераты по физике Тип: реферат |