Реферат: Фильтры нижних частот
Академия
Кафедра Физики
Реферат
Фильтры нижних частот
Орёл 2009
Содержание
Вступление
1. Полиномиальные ФНЧ с максимально плоскими характеристиками затухания (фильтры Баттерворта)
2. Полиномиальные ФНЧ с равно волновыми характеристиками затухания (фильтры Чебышева)
3. ФНЧ со всплесками затухания (фильтры Золотарёва)
Заключение
Литература
Вступление
В простейшем и наиболее часто используемом варианте фильтр включается между резистивными нагрузками (рисунок 1.).
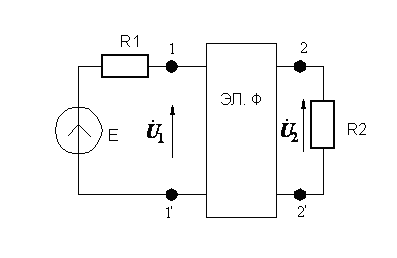
Рисунок 1.
Как уже отмечалось, для формирования требования к фильтру используется рабочее затухание
где
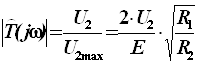
есть нормированная (рабочая) АЧХ фильтра. Кроме нормированной АЧХ для удобства расчётов может использоваться нормирование и других величин:
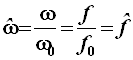- нормированная частота;
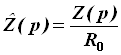- нормированное операторное сопротивление;
- нормированная индуктивность;
- нормированная ёмкость;
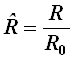- нормированное резистивное
сопротивление;
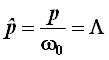- нормированный оператор Лапласа.
Здесь ω0, f0, R0 являются нормирующими величинами.
Если в результате решения задачи найдены нормированные величины, то денормирование производится по формулам:
; 
;
; 
; 
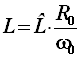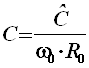Графики АЧХ и затухания идеальных ФНЧ показаны на рисунке 2.
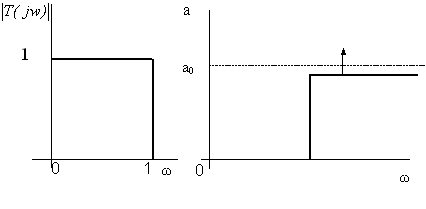
Рисунок 2.
Именно эти зависимости являются исходными при аппроксимации.
1. Полиномиальные ФНЧ с максимально плоскими характеристиками затухания (Баттерворта)
Полиномиальными называются ФНЧ, у которых ОПФ имеет вид:
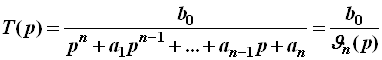(1)
Не трудно показать, что нормированная АЧХ полиномиального фильтра определяется следующим выражением:
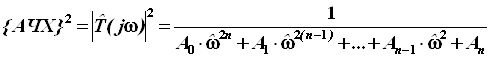(2)
Осуществим аппроксимацию по Тейлору АЧХ фильтра нижних частот.
При этом потребуем, чтобы
в точке 
=0, функция 
была равна единице, а все её │n-1│ первых производных
обращались бы в нуль. В этом случае АЧХ синтезируемого фильтра будет
максимально плоской.
Решение аппроксимации даёт следующий результат:
An=1; A1=A2=...=An-1=0; A0>0,
то есть любое вещественное положительное число (в противном случае нарушается УФР).
Следовательно, а(
) = 10lg 
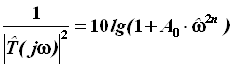(дБ).
Чрезвычайно удобно положить А0=(100,1Δа–1), где Δа - допустимая неравномерность затухания в полосе пропускания.
Так, при Δа = 3дБ получается100,1*3=100,3=2, следовательно А0=1 и формула приобретает вид:
a(
) = 10lg(1+
2n)
нормирующая частота ω0 в таком случае выбирается из условия:
а = Δа=3дБ.
Эту частоту принято
называть граничной частотой ПП фильтра. На рисунке 3 приведено семейство АЧХ 
для разных значений n.
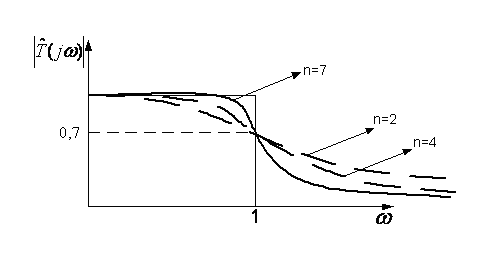
Рисунок 3.
Из него следует, что чем выше n, тем точнее аппроксимируется характеристика идеального фильтра.
Затухание рассматриваемых фильтров:
а = 10lg(1+2n)
в полосе задерживания,
где 
>>1 приближенно равно а
20nlg и возрастает со скоростью 6n дБ/октаву.(Октава – удвоение частоты).
Если заданы требования к ФНЧ, то выбор порядка фильтра при Δа = 3дБ осуществляется из условия, которое следует из графика на рисунке 4.
Рисунок 4.
В случае, когда Δа
3дБ и а0
10дБ, порядок фильтра может быть
подсчитан по формуле:
(3)
Нормированная операторная передаточная функция находится для выражения:
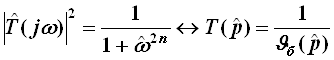
Полиномы 
, образующие определённый
подкласс полиномов Гурвица, получили название полиномов Баттерворта по имени
автора, предложившего максимально плоскую аппроксимацию АЧХ фильтров. Они
приводятся в справочной литературе, например в [Л2], стр. 290.
Реализация функции Т(р) может быть осуществлена любым из ранее рассмотренных методов. Однако для полиномиальных передаточных функций наибольшее распространение получила лестничная реализация, показанная на рисунке 5.
Рисунок 5.
Заметим, что число реактивных элементов этих схем всегда будет равно порядку передаточных функций Т(р), то есть числу n. Предпочтительное применение эти фильтры получили в случаях, когда надо уменьшить искажение формы передаваемых сигналов и не возникает необходимости в фазовом корректировании.
В настоящее время имеется большое число справочной литературы с табулированными решениями для фильтров Баттерворта, например [Л.2], стр. 291.
2. Полиномиальные ФНЧ с равноволновыми характеристиками затухания ( ф-ры Чебышева)
Пусть задана неравномерность затухания Δа, которая может быть на любой частоте полосы пропускания. Потребуем, чтобы при заданном n (числе элементов) затухания фильтра в полосе задержания, а0 было бы максимально возможным.
Решение задачи аппроксимации, соответствующей сформулированным требованиям, основано на экстремальных свойствах равномерного (чебышевского) приближения. Аналитическая запись такого решения имеет вид:
а = 10lg(1+A0Pn2()),
где Рп()=cos(n·arccos()) – полином Чебышева степени n.
Поскольку cos a=chj
, то существует и другая форма записи полиномов
Чебышева:
Рп(
)=ch(n·arch(
)).
В литературе приводятся
доказательства, что Рп(
)
действительно является полиномом степени n. Эти полиномы приводятся в справочной литературе, например в
[Л.2], стр. 290.
n=2; P2()=cos(2·arccos)=22-1;
n=5; Ps()=cos(5·arcos)=165-20
3+5.
В полосе пропускания, то
есть на интервале от 0 до 
квадрат полинома Чебышева
будет меняться в пределах [0;1], принимая
поочерёдно крайние значения (n+1) раз. При этом функция а на рассматриваемом интервале частот будет принимать
такое же число раз значения[0;Δа].
Рисунок 6.
На рисунке 6 приведены графики затухания чебышевских полиномиальных ФНЧ для значений n=2 и n=5 при одинаковых Δа.
Исследование функции а() позволяет
сделать ряд важных и интересных для практики выводов:
1. При одном и том же значении Δа увеличение порядка передаточной функции приводит к увеличению крутизны характеристики затухания за пределами полосы пропускания.
2. При неизменном значении n затухание вне полосы пропускания тем больше, чем больше Δа.
3. Наименьшие (равные 0) и наибольшие (равные Δа) значения затухания чередуются в полосе пропускания. Именно поэтому аппроксимацию по Чебышеву часто называют «равноволновой».
4. Затухание фильтра в полосе задержания с увеличением частоты возрастает монотонно.
По заданным требованиям к
характеристике затухания в полосе задерживания порядок ФНЧ Чебышева
рассчитывается так же, как и порядок ФНЧ Баттерворта, исходя из условия а(
)а0.
Решив данное неравенство относительно n получим:
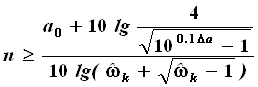(4).
Конструирование функции Т(р) по известной |T(j)|2 производится обычным
путём. Схемы лестничной реализации будут иметь тот же вид, что и у любого
другого полиномиального ФНЧ при одинаковом n.
Различие будет лишь в значениях величин параметров элементов. Табулированные решения по расчёту чебышевских ФНЧ приводятся в справочной литературе.
Преимущество фильтра Чебышева состоит в том, что при одинаковом количестве элементов и при одинаковом, Δа в полосе пропускания, этот фильтр имеет большее затухание в полосе задерживания по сравнению с фильтром Баттерворта.
3. ФНЧ со всплесками затухания (ф-ры Золотарева)
Отличительной особенностью характеристик затухания полиномиального ФНЧ является их монотонное возрастание по мере удаления от полосы пропускания. Однако, если необходимо синтезировать ФНЧ со значительным уровнем гарантированного затухания а0 и при узкой полосе перехода, то применение полиномиальных конструкций приводит к неоправданно большому количеству элементов в таких случаях имеет смысл обратиться к другим передаточным функциям, в частности имеющими нули полинома, а в полосе задержания всплеск затухания, то есть к функциям вида:
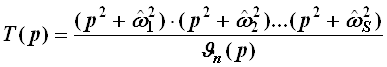(5)
где 
– полином Гурвица степени n; 
1, 2, ....., 
–
частоты в полосе задержания, где АЧХ фильтра обращается в нуль(затухание
принимает бесконечно большое значение, то есть имеет место его «всплеска»).
Частотная зависимость затухания имеет вид:
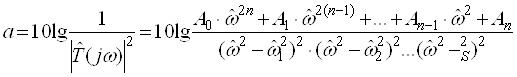(6)
Среди ФНЧ, передаточная функция которых имеет вид дроби (5), наибольшее распространение получили ФНЧ с изоэкстремальными характеристиками затухания или ФНЧ Золотарёва.
Требования к характеристике затухания ФНЧ такого типа формулируется следующим образом: затухание фильтра в полосе пропускания не должно превышать заданной величины Δа, а в полосе задержания быть не менее заданной величины а0.
В подобных случаях, при
аппроксимации характеристик затухания фильтра используется одна из задач
наилучшего приближения функций, сформулированная и решённая Е.И. Золотарёвым
(1847-1878), профессором Петербургского университета, учеником П.Л. Чебышева, а
именно задача о рациональной функции порядка n, значения которой по абсолютной величине в интервале -1 1 не превышали бы единицы, а в интервале || > 1 наименьшее по абсолютной величине её значение было бы
максимально возможным.
Соответствующая рациональная функция может быть названа дробью Золотарёва.
Если в выражение а = 10lg(1+A0Pn2()) под Pn() понимать дробь Золотарёва, то в
соответствии со свойствами последней наименьшее значение затухания такого
фильтра в полосе задержания будет максимально возможным по сравнению со всеми
другими фильтрами с теми же значениями.
График затухания ФНЧ с характеристиками Золотарёва, а также возможные схемы реализации приведены для случая n = 5 на рисунке 7.
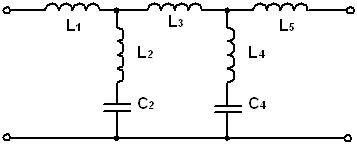
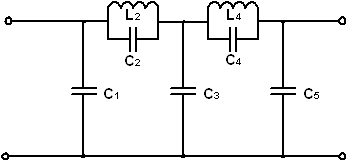
Рисунок 7.
Видно, что всплески затухания расположены так, что значения минимумов в полосе задержания оказываются одинаковыми и равными.
Фильтры с характеристиками Золотарёва (или просто ФНЧ Золотарёва) называют иногда эллиптическими, поскольку значения нулей и полюсов дроби Золотарёва выражаются через эллиптические функции.
Решения, связанные с расчётом ФНЧ Золотарёва, в настоящее время табулированы и доведены до схем и значений параметров элементов (см. Л.2, стр. 292-295).
Эффективность ФНЧ Золотарёва может быть подтверждена примером, где к ФНЧ предъявляются довольно жёсткие требования.
Δа=0,01 Hп, a0=5.0 Hп, 
к=1,08.
(7)
Расчёт порядка n различных фильтров, удовлетворяющий указанным требованиям, даст следующие результаты:
Число элементов равняется соответственно 7, 18, 80.
В данном примере ФНЧ Золотарёва явно оказывается вне конкуренции.
Заключение
Подробное изучение свойств различных фильтров позволяет сделать вывод, что в отдельных частных случаях при сравнительно широких полосах перехода минимальным числом элементов может обладать полиномиальный ФНЧ. Могут иметь место такие ситуации, когда по числу элементов ФНЧ Золотарёва и полиномиальный ФНЧ Чебышева оказываются одинаковыми. Тогда предпочтение отдают тому типу, который более полно удовлетворяет другим требованиям (габариты, технология изготовления и т.д.).
Литература, используемая для подготовки лекции
1. Белецкий А.Ф. «Теория линейных электрических цепей » Москва 1986 c 368-395