Лабораторная работа: Цифрова обробка сигналів
Міністерство освіти та науки України
Житомирський інженерно-технологічний інститут
Кафедра АУТС
Розрахунково-графічна робота
“Цифрова обробка сигналів”
Житомир 2006
Задача №1.
Знайти згортку послідовностей x(n) і y(n) двома способами: прямим обчисленням і з використанням z-перетворення. Результат обчислень представити графічно.
таблиця 1.1
| N | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| x(n) | 3 | 0 | -1 | 1 | 2 | 3 | 0 |
| y(n) | 1 | 0 | 2 | -1 | -2 | 0 | 2 |
Для побудови графіків я використовую програму MathCAD 2001і Professional.
Знайдемо згортку прямим обчисленням:
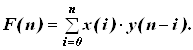
F(0)=x(0)×y(0) = 3;
F(1)=x(0)×y(1)+x(1)×y(0) = 0+0 = 0;
F(2)=x(0)×y(2)+x(1)×y(1)+x(2)×y(0) = 3×2+0×0+(-1) ×1 = 5;
F(3)=x(0)×y(3)+x(1)×y(2)+x(2)×y(1)+x(3)×y(0) = -3+0+0+1 = -2;
F(4)=x(0)×y(4)+x(1)×y(3)+x(2)×y(2)+x(3)×y(1)+x(4)×y(0) = -6+0-2+0+2= -6;
F(5)=x(0)×y(5)+x(1)×y(4)+x(2)×y(3)+x(3)×y(2)+x(4)×y(1)+x(5)×y(0) = 0+0+1+2+0+3 = 6;
F(6)=x(0)×y(6)+x(1)×y(5)+x(2)×y(4)+x(3)×y(3)+x(4)×y(2)+x(5)×y(1)+x(6)×y(0) = 6+0+2-1+4+0+0 = 11.
F(7)= x(0)×y(7)+x(1)×y(6)+x(2)×y(5)+x(3)×y(4)+x(4)×y(3)+x(5)×y(2)+x(6)× y(1)+x(7)×y(0) = 0+0-2-2+6+0 = 2;
F(8)=x(0)×y(8)+x(1)×y(7)+x(2)×y(6)+x(3)×y(5)+x(4)×y(4)+x(5)×y(3)+x(6)×y(2)+x(7)×y(1)+x(8)×y(0) =0+0-2+0-4-3+0+0+0 = -9;
F(9)=x(0)×y(9)+x(1)×y(8)+x(2)×y(7)+x(3)×y(6)+x(4)×y(5)+x(5)×y(4)+x(6)×y(3)+x(7)×y(2)+x(8)×y(1)+x(9)×y(0)= 0+0+0+2+0-6+0+0+0+0 = -4;
F(10)= x(0)×y(10)+x(1)×y(9)+x(2)×y(8)+x(3)×y(7)+x(4)×y(6)+x(5)×y(5)+x(6)× y(4)+x(7)×y(3)+x(8)×y(2)+x(9)×y(1)+x(10)×y(0) = 0+0+0+0+4+0+0+0+0+0+0 = 4;
F(11)= x(0)×y(11)+x(1)×y(10)+x(2)×y(9)+x(3)×y(8)+x(4)×y(7)+x(5)×y(6)+x(6)× y(5)+x(7)×y(4)+x(8)×y(3)+x(9)×y(2)+ x(10)×y(1)+x(11)×y(0) = 0+0+0+0+0+6+0+0+0+0+0+0 = 6;
F(12)= x(0)×y(12)+x(1)×y(11)+x(2)×y(10)+x(3)×y(9)+x(4)×y(8)+x(5)×y(7) +x(6)× y(6)+x(7)×y(5)+x(8)×y(4)+x(9)×y(3)+ x(10)×y(2)+x(11)×y(1)+x(12)×y(0) = 0+0+0+0+0+0+0+0+0+0+0+0+0 = 0;
F(n)={3;0;5;-2;-6;6;11;2;-9;-4;4;6;0}
Знайдемо згортку з використанням z-перетворення:
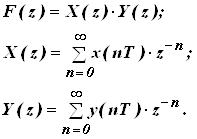
![]()
Перемножаю і отримую результат z-перетворення:

f(0)=3 f(4)=-6 f(8)=-9 f(12)=0
f(1)=0 f(5)=6 f(9)=-4
f(2)=5 f(6)=11 f(10)=4
f(3)=-2 f(7)=2 f(11)=6
Результати обчислень представляю графічно:



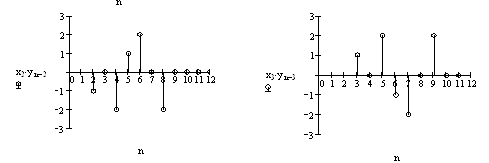
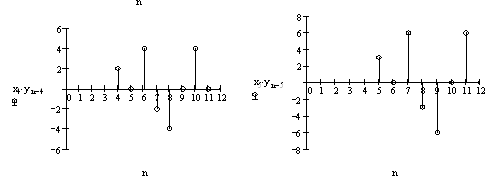

Задача №2
Цифровий фільтр описується наступним різницевим рівнянням:
![]()
Період дискретизації Т= 2мс.
Знайти системну функцію фільтра, імпульсну характеристику, частотну характеристику (аналітичні вирази). Зобразити розташування нулів і полюсів системної функції на z-площині. Побудувати графік АЧХ фільтра, зобразити структурну схему фільтра, з'ясувати, чи стійкий даний фільтр. Побудувати початкову частину імпульсної характеристики фільтра (не менш 30 відліків).
Знайдемо системну функцію фільтра:
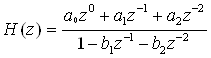
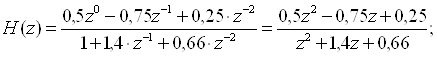
Знайдемо нулі і полюси системної функції:
Нулі: ![]()
![]()
![]()
![]()
Полюса
![]()
![]()
Отже корені комплексні:
![]()
![]()
Розташування нулів та полюсів системної функції на z-площині (рис. 2.1):
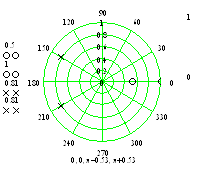
рис. 2.1
По даному графіку можна зробити висновок, що наш фільтр стійкий, оскільки його полюси лежать в межах кола одиничного радіуса.
Знайдемо імпульсну характеристику:

Кінцевий результат:
![]()
Визначимо початкову частину імпульсної характеристики фільтра (30 відліків) (таблиця 2.1. і рис. 2.2):
таблиця 2.1.
| n | h(n) | n | h(n) | n | h(n) |
| 0 | 0,12 | 10 | -0,33 | 20 | -0,05 |
| 1 | -1,46 | 11 | 0,13 | 21 | 0,04 |
| 2 | 1,96 | 12 | 0,04 | 22 | -0,02 |
| 3 | -1,78 | 13 | -0,13 | 23 | 0,08 |
| 4 | 1,20 | 14 | 0,16 | 24 | 0,05 |
| 5 | -0,50 | 15 | -0,14 | 25 | -0,01 |
| 6 | -0,08 | 16 | 0,09 | 26 | 0,01 |
| 7 | 0,44 | 17 | -0,03 | 27 | -0,01 |
| 8 | -0,57 | 18 | -0,01 | 28 | 0,06 |
| 9 | 0,5 | 19 | 0,04 | 29 | -0,02 |
30 -0,02
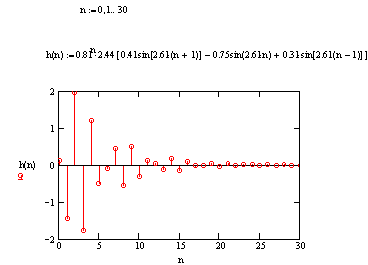
рис. 2.2
Знайдемо частотну характеристику:

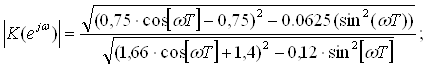
Побудуємо графік АЧХ фільтра (рис. 2.3):
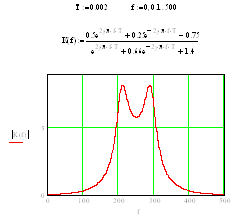
рис. 2.3
Структурна схема фільтра (рис. 2.4):

рис. 2.4