Контрольная работа: Основы теории излучения звуковых волн
Основы теории излучения звуковых волн
Основным устройством, применяемым для излучения звука, является громкоговоритель прямого излучения, использующий для преобразования механических колебаний в акустические мембрану, которую часто называют диффузором (т.е. рассеивателем звука).
В общем случае диффузор может иметь сложную форму. Однако, проведенные эксперименты показали, что основне особенности процесса излучения звукових волн дифузором нетрудно получить с достаточной для практики точностью, если заменить его плоской пластиной.
Механизм излучения звукових волн прост. Колеблющаяся мембрана приводит в движение примыкающие к ней частицы воздуха, создавая периодическое сжатие и разрежение.
Эти колебания дваления передаються соседним слоям воздуха, образуя волны, распространяющиеся со скоростью звука. Задача состоит в том, чтобы описать этот процесс количественно.
Рассмотрим частный случай – излучение пульсирующей сферы. В этом случае поверхость сферы совершает радиальные колебания, возбуждая в окружающей среде сферические звукове волны.
Звуковое давление:
![]() .
.
Если радиус пульсирующей
сферы равен![]() и амплитуда скорости колебаний
и амплитуда скорости колебаний ![]() , то производительность источника
, то производительность источника ![]() . Чтобы
определить постоянную
. Чтобы
определить постоянную ![]() в выражении для звукового
давления, воспользуемся уравнением движения среды. В нашем случае:
в выражении для звукового
давления, воспользуемся уравнением движения среды. В нашем случае:
![]() .
.
Производная:
![]() .
.
Подставляя в уравнение
движения это выражение и сокращая на ![]() , получим:
, получим:
![]() .
.
Если ![]() « λ, то 1/r2»
к/r и при r = а:
« λ, то 1/r2»
к/r и при r = а:
![]() или
или ![]() .
.
Подставляя значение А в выражение для звукового давления, получим:
![]()
![]() .
.
Выражение определяет звуковое давление, создаваемое так называемым точечным источником.
Зная звуковое давление
нетрудно вычислить излучаемую мощность. Для этого найдем среднее за период
значение интенсивности звука, вычисленное для расстояния ![]() от центра пульсирующей
сферы:
от центра пульсирующей
сферы:
![]() .
.
Излучаемую мощность получим, умножив интенсивность звука на площадь сферы радиуса r:
![]() .
.
Полученные формулы для поля точечного источника позволяют рассчитать поле излучателей другой конфигурации и размеров.
Для этого поверхность исследуемого излучателя разбивается на множество участков малых размеров, каждый участок рассматривается как точечный излучатель и звуковое давление в заданной точке пространства находится путем сложения полей всех точечных излучателей в этой точке пространства.
Другими словами, звуковое давление в заданной точке находим путем интегрирования выражения по поверхности излучателя.
Конфигурация излучающей поверхности может быть достаточно сложной и, потому, не всегда удаётся выполнить интегрирование. Можно получить приближенное решение задачи, заменяя реальный излучатель излучателем более простой конфигурации.
Так, достаточно хорошее приближение к реальному громкоговорителю с коническим диффузором можно получить, заменяя реальный диффузор круглым плоским диском.
Круглый диск в бесконечном экране. Применив указанную методику к круглому диску, расположенному в отверстии бесконечного плоского экрана, получили выражение для звукового давления:
![]() ,
,
где ![]() функция Бесселя первого
рода первого порядка от аргумента
функция Бесселя первого
рода первого порядка от аргумента ![]() ;
;
![]() – радиус диска,
– радиус диска,
![]() - волновое число;
- волновое число;
![]() - угол между осью диска и
направлением на точку наблюдения.
- угол между осью диска и
направлением на точку наблюдения.
При ![]() звуковое давление:
звуковое давление:
![]() .
.
Отношение ![]() называют коэффициентом
направленности
называют коэффициентом
направленности ![]() . График, изображающий зависимость
коэффициента направленности от угла
. График, изображающий зависимость
коэффициента направленности от угла ![]() , называют нормированной
диаграммой направленности излучения громкоговорителя.
, называют нормированной
диаграммой направленности излучения громкоговорителя.
На рис. 1 показана
диаграмма направленности круглого диска в экране, рассчитанная для трёх
значений ![]() :
0.25, 2.5, 5.
:
0.25, 2.5, 5.
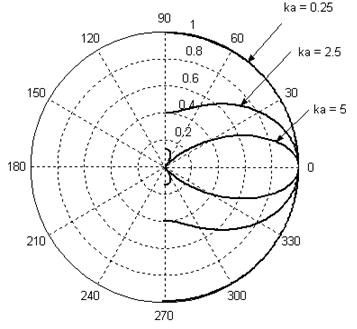
Диаграмма направленности
излучения диска радиуса а в плоском экране для разных значений ![]()
(Если принять ![]() , то диаграмма
соответствует частотам 136 Гц, 1360 Гц и 2780 Гц ).
, то диаграмма
соответствует частотам 136 Гц, 1360 Гц и 2780 Гц ).
Приведенные на рис. 1 диаграммы показывают, что с повышением частоты направленность излучения в направлении оси диска растёт.
При расположении
слушателей в стороне от оси диска (![]() ) это будет проявляться в
относительном уменьшении уровня высоких частот.
) это будет проявляться в
относительном уменьшении уровня высоких частот.
При описании диаграмм
направленности часто пользуются понятием индекс направленности, который равен ![]() .
.
С диаграммой направленности связано такое понятие, как угол излучения громкоговорителя. Углом излучения громкоговорителя называют угол, в пределах которого индекс направленности спадает менее чем на 10дБ.
В нашем примере для частоты 2780 Гц угол излучения равен ~ 70о.
Наконец, ещё одно понятие, характеризующее направленные свойства излучателя.
Это – коэффициент осевой концентрации. Коэффициентом осевой концентрации называют отношение акустической мощности, излучаемой ненаправленным излучателем, к акустической мощности, излучаемой направленным излучателем, если он создаёт на заданном расстоянии такое же осевое давление, как ненаправленный.
Мощность, излучаемая ненаправленным излучателем:
![]() .
.
Мощность, излучаемая направленным излучателем с диаграммой направленности, обладающей осевой симметрией:
![]()
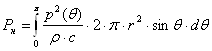 .
.
Коэффициент осевой концентрации:
Колебания диффузора легче создать в вакууме, чем в воздушной среде, т.к. воздух оказывает сопротивление колебаниям.
Это сопротивление
добавляется к механическому сопротивлению диффузора и называется сопротивлением
излучения![]() .
Для колеблющегося диска в экране получены такие выражения:
.
Для колеблющегося диска в экране получены такие выражения:
![]()
![]()
![]()
![]() ,
,
где ![]() ,
, ![]() - безразмерные
величины,
- безразмерные
величины,
![]() - площадь диска,
- площадь диска,
![]() - функция Бесселя 1-го рода
первого порядка от аргумента
- функция Бесселя 1-го рода
первого порядка от аргумента ![]() ,
,
![]() функция Струве первого порядка.
функция Струве первого порядка.
Полная излучаемая
мощность ![]() .
.
В общем случае сопротивление излучения – комплексная величина. Следовательно, имеется активная составляющая мощности, определяющая энергию, уходящую в бесконечность, и реактивная составляющая, определяющая запас энергии в звуковом поле.
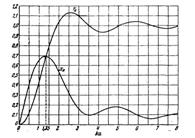
Поведение безразмерных
коэффициентов ![]() и
и ![]() в зависимости от значений
параметра
в зависимости от значений
параметра ![]() для
диска в экране показано на рис. 2.
для
диска в экране показано на рис. 2.
В области низких частот ![]() , тогда
активная составляющая сопротивления излучения
, тогда
активная составляющая сопротивления излучения ![]() , реактивная составляющая
, реактивная составляющая ![]()
Откуда присоединенная
масса воздуха ![]() . При
. При ![]()
![]() , а
, а ![]() .
.
Следует отметить, что приведенные формулы получены в предположении, что диск совершает колебания как абсолютно жесткое тело. Для реальных диффузоров это предположение справедливо, если размеры диффузора меньше длины волны звуковых колебаний.
Такой режим работы диффузора называют поршневым. На высоких частотах на поверхности диффузора могут возникать стоячие волны и разные точки поверхности будут двигаться с различными скоростями.
Граничную частоту, до которой режим работы диффузора можно считать поршневым, можно оценить по формуле:
![]() ,
,
где ![]() радиус диффузора.
радиус диффузора.
Реальные головки громкоговорителей имеют диффузор чаще всего конической формы. Математическое исследование работы такого диффузора значительно сложнее, чем диска.
Приведем результаты приближенного анализа. Осевое давление может быть описано формулой:
![]() ,
,
где ![]() - амплитуда осевого
давления, создаваемого диском радиуса а;
- амплитуда осевого
давления, создаваемого диском радиуса а;
![]() - функция, учитывающая влияние
конусности диффузора;
- функция, учитывающая влияние
конусности диффузора;
![]() - длина образующей конуса;
- длина образующей конуса;
![]() - угол между осью диффузора и
образующей (см. рис. 3 а).
- угол между осью диффузора и
образующей (см. рис. 3 а).
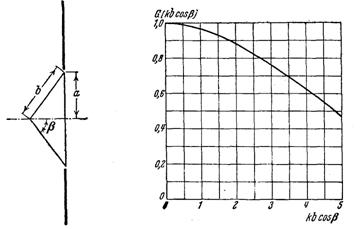
На рис. 3 б приведен
график функции ![]() . Из графика следует, что при
. Из графика следует, что при ![]() , т.е. для
волн, длина которых велика по сравнению с размерами диффузора, звуковое поле
конического диффузора мало отличается от поля диска таких же размеров.
, т.е. для
волн, длина которых велика по сравнению с размерами диффузора, звуковое поле
конического диффузора мало отличается от поля диска таких же размеров.
При ![]() конус создаёт меньшее
осевое давление, чем диск при той же скорости колебаний. Диаграммы
направленности излучения конического диффузора менее острые, чем у диска (см.
рис. 4). Таким образом, результаты, полученные для диска, могут быть
распространены на реальные излучатели.
конус создаёт меньшее
осевое давление, чем диск при той же скорости колебаний. Диаграммы
направленности излучения конического диффузора менее острые, чем у диска (см.
рис. 4). Таким образом, результаты, полученные для диска, могут быть
распространены на реальные излучатели.
Аналогичные исследования были проведены для осциллирующего диска без экрана и для диска, помещенного в отверстии ящика. Ненкоторые результаты этих исследований представлены в таблице 1.
Как следует из таблицы 1, наиболее эффективный излучатель – осциллирующий диск в отверстии бесконечно протяженного плоского экрана.
Таблица 1. Некоторые характеристики простейших излучателей
| Характеристики излучателя | Источник излучения | ||
| Осциллирующий диск в экране | Осциллирующий диск без экрана | Осциллирующий диск в ящике | |
|
Осевое давление |
|
|
|
|
|
1 |
При |
При |
| Диаграмма направленности | Полуокружность | Восьмерка | - |
|
Активная составляющая сопротивления
излучения |
|
|
|
| Присоединенная масса |
|
|
|
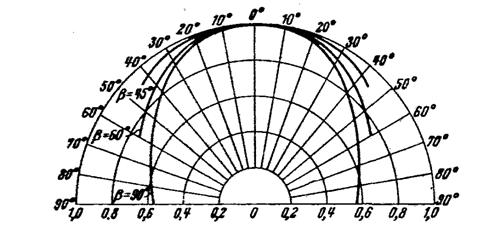
Диаграммы направленности конического диффузора при разных значениях угла β