Курсовая работа: Оптимизация алгоритмов поиска
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
Государственное образовательное учреждение высшего профессионального образования "Воронежский государственный технический университет"
Радиотехнический факультет
Кафедра радиотехники
Специальность 210302 "Радиотехника"
Оптимизация алгоритмов поиска
Выполнил студент гр. РТ-041 Д.С. Чёткин
Проверил доцент кафедры В.П. Литвиненко
Воронеж 2007
Содержание
Введение. 4
1. Разработка оптимального дихотомического алгоритма поиска при равновероятном распределении вероятностей и числе событий М=16. 5
2. Разработка оптимального алгоритма поиска для экспоненциального закона распределения вероятностей при М=16. 7
3. Разработка оптимального алгоритма поиска экспоненциального закона распределения при числе измерений от N=15 до N=log2M.. 9
4. Разработка оптимального алгоритма поиска для 9-го варианта распределения при числе измерений от N=1 до 15. 12
Заключение. 19
Список литературы.. 20
Введение
Скрытность характеризует затраты
(времени, средств), необходимые для выявления реасобытия с заданной
достоверностью (вероятностью правильного решения, доверительной вероятностью ![]() ).
).
При формировании оценки скрытности случайного события в качестве оправной принята двухальтернативная пошаговая поисковая процедура, сущность которой заключается в следующем.
Множество Х с соответствующим
законом распределения вероятностей разбивается на два подмножества ![]() и
и ![]() (верхний
индекс - номер разбиения). Двоичный измеритель проводит двоичное измерение, выявляя,
в каком подмножестве находится реасобытие (его след). Затем подмножество, в
котором обнаружено реасобытие (на рис.2.1. это
(верхний
индекс - номер разбиения). Двоичный измеритель проводит двоичное измерение, выявляя,
в каком подмножестве находится реасобытие (его след). Затем подмножество, в
котором обнаружено реасобытие (на рис.2.1. это ![]() ), вновь разбивается на два
подмножества
), вновь разбивается на два
подмножества ![]() и
и ![]() и выявляется след реасобытия в
одном из них. Процедура заканчивается, когда в выделенном подмножестве
оказывается одно событие. Поиск может быть последовательным и дихотомическим. В
первом алгоритме (
и выявляется след реасобытия в
одном из них. Процедура заканчивается, когда в выделенном подмножестве
оказывается одно событие. Поиск может быть последовательным и дихотомическим. В
первом алгоритме (![]() ) производится последовательный
перебор состояний от первого до последнего, пока не встретится реасобытие.
) производится последовательный
перебор состояний от первого до последнего, пока не встретится реасобытие.
Второй алгоритм поиска (![]() ) предполагает
разделение всего множества состояний пополам, проверку наличия реасобытия в
каждой из этих частей, затем разделение выбранной половины множества X на две равные части с проверкой наличия в них реасобытия и
так далее. Поиск заканчивается, когда в выделенном подмножестве оказывается
одно событие.
) предполагает
разделение всего множества состояний пополам, проверку наличия реасобытия в
каждой из этих частей, затем разделение выбранной половины множества X на две равные части с проверкой наличия в них реасобытия и
так далее. Поиск заканчивается, когда в выделенном подмножестве оказывается
одно событие.
Существует несколько способов минимизации двоичных поисковых процедур. Примерами могут служить методы Циммермана-Хафмена и Шеннона-Фоно. Оптимизировать алгоритм можно по различным параметрам с учетом стоимости измерения и без. В данной лабораторной работе исследовали оптимизацию дихотомического алгоритма поиска по наименьшей величине средней скрытности.
1. Разработка оптимального дихотомического алгоритма поиска при равновероятном распределении вероятностей и числе событий М=16
Включите режим дихотомического
поиска. Установите число событий ![]() при равномерном распределении
вероятностей и задайте число измерений
при равномерном распределении
вероятностей и задайте число измерений ![]() . Разработайте оптимальный
алгоритм поиска, задайте его на наборном поле, проведите моделирование,
определите потенциальную скрытность.
. Разработайте оптимальный
алгоритм поиска, задайте его на наборном поле, проведите моделирование,
определите потенциальную скрытность.
В данном случае наиболее оптимальным алгоритмом поиска является алгоритм разработанный по принципу Шеннона-Фано. Данный метод предполагает исходное множество элементов с заданным распределением разбить на два подмножества с номерами 0 и 1 так, чтобы вероятности попадания в них были максимальны близки (в идеале пополам). Затем каждое из полученных подмножеств отдельно разбивается на два подмножества с тем же условием и номерами с 00,01,10,11. Разбиение заканчивается когда все элементы подмножества будут иметь только по одному элементу.
В результате разработан оптимальный алгоритм поиска для равновероятного закона распределения вероятностей.
Проведем расчет потенциальной скрытности для равновероятного закона распределения вероятностей:
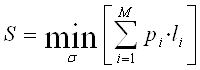 (1)
(1)
В результате для данного случая:
![]()
В результате получено простое выражение для определения потенциальной скрытности равномерного закона распределения, который при дихотомическом алгоритме поиска не зависит от перебора комбинации измерений, а только от вида дерева поиска.
2. Разработка оптимального алгоритма поиска для экспоненциального закона распределения вероятностей при М=16
Выберите экспоненциальное
распределение вероятностей событий вида ![]() ,
, ![]() ,
, ![]() - нормирующий множитель, при том
же
- нормирующий множитель, при том
же ![]() , что и
в пункте 1. Определите оптимальный алгоритм поиска, задайте его на наборном
поле, проведите моделирование, определите потенциальную скрытность.
, что и
в пункте 1. Определите оптимальный алгоритм поиска, задайте его на наборном
поле, проведите моделирование, определите потенциальную скрытность.
Первоначально оставим дерево поиска таким же, что в предыдущем пункте. «Print Screen» программы «Poisk» для данного случая для экспоненциального закона распределения.
Глядя на ход кривой снятия неопределенности приходим выводу, что ее ход является неоптимальным. Используя известные алгоритмы оптимизации поиска приходим к тому, что в данном случае оптимальным алгоритмом поиска является вовсе не дихотомический алгоритм при любых комбинациях нахождения реасобытия, а последовательный. Для данного случая он является оптимальным, так как первым измерением проверяется наиболее вероятное, затем следующее и так пока не останется неопределенности принятия решения.
Доказательство использования последовательного алгоритма поиска. Для этого используется метод Циммермана-Хаффмена. Данный метод оптимизации состоит из двух этапов: «Заготовительные операции» и «Считывание». Более подробно про это говорится в книге [1].
Так как показатель степени больше 1, а это удовлетворяет неравенству:
![]()
Где λ – показатель степени распределения вероятностей, равный 1, то для данного случая оптимальным является последовательный алгоритм поиска.
![]()
В результате выполнения данного пункта показано, что оптимальным является последовательный алгоритм поиска. Сравнивая результаты выполнения двух пунктов приходи к выводу, что для каждого закона распределения вероятностей имеется свой оптимальный алгоритм поиска либо последовательный, либо дихотомический, либо комбинированный алгоритм поиска.
3. Разработка оптимального алгоритма поиска экспоненциального закона распределения при числе измерений от N=15 до N=log2M
Для экспоненциального
распределения вероятностей из пункта 2 последовательно уменьшая максимальное
число измерений от ![]() до
до ![]() , разработайте оптимальные алгоритмы
поиска и по результатам моделирования определите соответствующие значения
среднего числа измерений
, разработайте оптимальные алгоритмы
поиска и по результатам моделирования определите соответствующие значения
среднего числа измерений ![]() .
.
При N=15 из предыдущего пункта оптимальным является последовательный алгоритм поиска и для него значение среднее значение двоичных измерений определяется так же как и для потенциальной скрытности. Значение Rcp представлено в таблице 1.
Таблица 1 – Зависимость среднего числа измерений
от числа измерений при оптимальных алгоритмах поиска
| ТN | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 111 | 112 | 113 | 114 | 115 |
| КRср | ннельзя | 4 | 22.875 | 22.4062 | 22. 2011 | 22.0956 | 22.0343 | .2.0077 | 22.0038 | 22.0013 | 12.0003 | 11,9998 | 11.9997 |
Далее при N=14.
Проведем расчет потенциальной скрытности для каждого случая по формуле 1:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
При числе измерений равному 3-м, разработать алгоритм поиска невозможно, так это не удовлетворяет условию реализуемости поиска, а именно:
![]() (2)
(2)
В результате построен график зависимости среднего числа измерений от числа измерений представленный на рисунке 8.
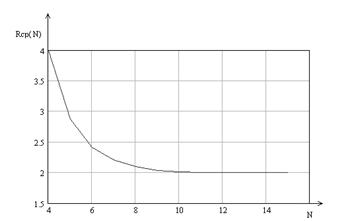
Рисунок 8 – Зависимость среднего числа измерений от числа измерений для экспоненциального закона распределения вероятности
4. Разработка оптимального алгоритма поиска для 9-го варианта распределения при числе измерений от N=1 до 15
Для своего варианта
распределения вероятностей при числе событий ![]() разработайте оптимальный алгоритм
поиска, постройте дерево поиска, объясните его форму, чем она обусловлена?
разработайте оптимальный алгоритм
поиска, постройте дерево поиска, объясните его форму, чем она обусловлена?
На наборном поле задайте
оптимальный полный алгоритм поиска. Последовательно исключая последние
измерения (до ![]() ), рассмотрите зависимость
среднего числа измерений
), рассмотрите зависимость
среднего числа измерений ![]() , вероятности неполного решения
, вероятности неполного решения ![]() и остаточной
скрытности
и остаточной
скрытности ![]() от
продолжительности поиска
от
продолжительности поиска ![]() . Результаты представлены в
таблице 2.
. Результаты представлены в
таблице 2.
Таблица 2 – Зависимость среднего числа измерений,
остаточной скрытности, вероятности неопределенности от числа измерений
| n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| R | 4 | 3.775 | 4.325 | 4.725 | 5.1625 | 5.375 | 5.5 | 5.65 | 5.7 | 5.7625 | 5.8 | 5.8 | |||
| Pнеоп | 0.55 | 0.7625 | 0.875 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sост | 0.801 | 0.785 | 0.791 | 0.802 | 0.814 | 0.826 | 0.837 | 0.848 | 0.858 | 0.868 | 0.877 | 0.885 | 0.893 | 0.901 |
В данной таблице Sост считалось при доверительной вероятности 0.9. «Print Screen» программы «Poisk» при различных значениях числа измерений представлен на рисунках 8-11.
При числе измерений меньше 4-х появляется вероятность неполного решения, связанная с тем, что невозможно проверить все события. В результате приходится проверять не все, оптимальным вариантом будет проверка наиболее вероятных событий. «Print Screen» программы «Poisk» при числе измерения меньше 3-х представлена на рисунке 12.
Построим график зависимости потенциальной скрытности от числа измерения, который представлен на рисунке 13.
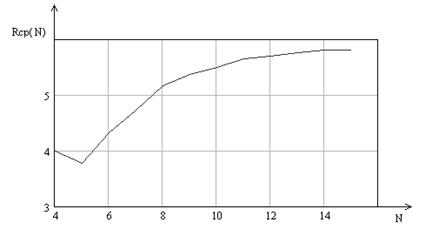
Рисунок 13 – Зависимость среднего числа измерений от числа измерений для 9-го закона распределения вероятности
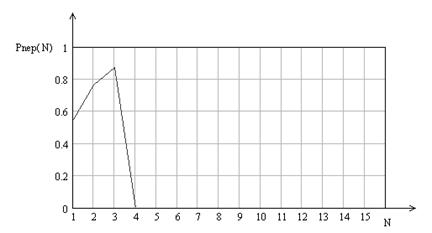
Рисунок 14 – Зависимость вероятности неполного решения от числа измерений для 9-го закона распределения вероятности
Далее требуется провести расчет остаточной скрытности от числа измерений.
![]() (3)
(3)
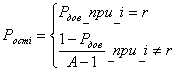 (4)
(4)
Доверительную вероятность будем менять в пределах 0.7÷0.9. В результате получен график зависимости остаточной скрытности от числа измерений, который представлен на рисунке 15.
Ност(Pдов) Pдов=0.9
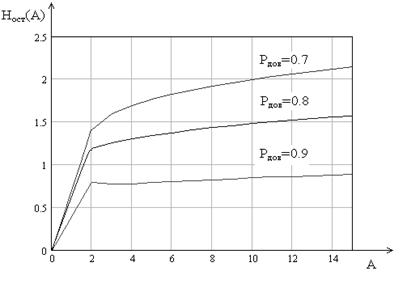
Рисунок 15 – Зависимость остаточной скрытости при значениях доверительной вероятности 0.7÷0.9
Из представленного выше графика можно сделать вывод, что Pдов следует выбирать близким к единице, это приведет к уменьшению остаточной скрытности, однако не всегда такое возможно.
Далее предполагается построить график зависимости остаточной скрытности при фиксированных значениях числа измерений. Проведем построение при 4,8,16, соответствующий график приведен на рисунке 16.
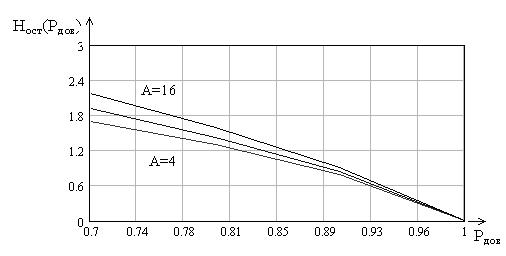
Рисунок 16 – Зависимость остаточной скрытости при значениях числа измерений 4,8,16
Из данного графика следует что, при большом числе измерений остаточная скрытность выше, хотя по логике большее число измерений приведет к уменьшению вероятности неопределенности решения.
Заключение
В данной работе были проведены исследования оптимизации дихотомического алгоритма поиска с помощью программы Poick. Проведено сравнение с последовательным алгоритмом. Исследован вид КСН при равномерном, экспоненциальном и заданном по варианту распределении событий. Наработаны навыки в обращении с программой Poick.
В ходе выполнения лабораторной работы была произведена разработка оптимальных алгоритмов поиска для последовательного и дихотомического алгоритмов поиска.
Проведен расчет кривой снятия неопределенности и установлено, что в некоторых случаях более правильнее использовать последовательный алгоритм поиска, а в других дихотомический. Но это может быть связано только с исходным распределением вероятности.
Правильность работы программы Poisk потверждена с помощью расчётов проведённых в пакете программ Matcard 2001.
Список литературы
1. Основы теории скрытности: учебное пособие для студентов специальности 200700 «Радиотехника» дневной формы обучения / Воронежский государственный технический университет; Сост.З.М. Каневский, В.П. Литвиненко, Г.В. Макаров, Д.А. Максимов; под редакцией З.М. Каневского. Воронеж, 2006. 202с.
2. Методические указания к лабораторным работам «Исследование алгоритмов поиска» по дисциплине «Основы теории скрытности» для студентов специальности 200700 «Радиотехника» дневной форм7 обучения / Воронежский государственный технический университет; сост.З.М. Каневский, В.П. Литвиненко. Воронеж, 2007.54с.
3. СТП ВГТУ 005-2007. Курсовое проектирование. Организация, порядок, оформление расчетно-пояснительной записки и графической части.