Контрольная работа: Основная задача механики
Механическая система под действием сил тяжести приходит в движение из состояния покоя, начальное положение системы показано на рис. 1. Учитывая сопротивление качению тела 3, катящегося без скольжения, пренебрегая другими силами сопротивления и массами нитей, предполагаемых нерастяжимыми, определить скорость тела 1 в тот момент времени, когда пройденный путь станет равным s.
В задании приняты следующие обозначения: m1, m2, m3, m4 – массы тел 1, 2, 3, 4; R3 – радиус большой окружности; δ – коэффициент трения качения.
Необходимые для решения данные приведены в таблице 1. Блоки и катки считать сплошными однородными цилиндрами. Наклонные участки нитей параллельны соответствующим наклонным плоскостям.
Таблица 1.
|
m1, кг |
m2, кг |
m3, кг |
m4, кг |
R3 |
δ, см |
s, м |
| m | 1/2m | 5m | 4m | 25 | 0,20 | 2 |
Решение
Применим теорему об изменении кинетической энергии системы:
![]() (1)
(1)
где T0 и T –
кинетическая энергия системы в начальном и конечном положениях; ![]() - сумма работ внешних сил,
приложенных к системе;
- сумма работ внешних сил,
приложенных к системе; ![]() - сумма работ
внутренних сил системы.
- сумма работ
внутренних сил системы.
Для рассматриваемых систем, состоящих из абсолютно твердых тел, соединенных нерастяжимыми нитями,
![]()
Так как в начальном положении система находится в покое, то Т0=0.
Следовательно, уравнение (1) принимает вид:
![]() (2)
(2)
Кинетическая энергия рассматриваемой системы Т в конечном ее положении (рис.2) равна сумме кинетических энергий тел 1, 2, 3 и 4:
Т = Т1 + Т2 + 4Т3 + Т4. (3)
Кинетическая энергия груза 1, движущегося поступательно,
![]() (4)
(4)
Кинетическая энергия барабана 2, совершающего вращательное движение,
![]() , (5)
, (5)
где J2x – момент инерции барабана 2 относительно центральной продольной оси:
![]() , (6)
, (6)
w2 – угловая скорость барабана 2:
![]() .(7)
.(7)
После подстановки (6) и (7) в (5) выражение кинетической энергии барабана 2 принимает вид:
![]() . (8)
. (8)
Кинетическая энергия колеса 3, совершающего плоскопараллельное движение:
![]() , (9)
, (9)
где VC3 – скорость центра тяжести С3 барабана 3, J3x – момент инерции барабана 3 относительно центральной продольной оси:
![]() , (10)
, (10)
w3 – угловая скорость барабана 3.
Мгновенный центр скоростей находится в точке СV. Поэтому
![]() , (11)
, (11)
![]() . (12)
. (12)
Подставляя (10), (11) и (12) в (9), получим:
![]() . (13)
. (13)
Кинетическая энергия груза 4, движущегося поступательно
![]() . (14)
. (14)
Кинетическая энергия всей механической системы определяется по формуле (3) с учетом (4), (8), (13), (15):
![]()
Подставляя и заданные значения масс в (3), имеем:
![]()
или
![]() . (15)
. (15)
Найдем сумму работ всех внешних сил, приложенных к системе, на заданном ее перемещении (рис. 3).
Работа силы тяжести ![]() :
:
![]() (16)
(16)
Работа силы тяжести ![]() :
:
![]() (17)
(17)
Работа пары сил сопротивления качению ![]() :
:
![]() (18)
(18)
где
![]() (19)
(19)
![]() (20)
(20)
![]() (21)
(21)
Подставляя (19), (20) и (21) в (18), получаем:
![]() (22)
(22)
Работа силы тяжести ![]() :
:
![]() (17)
(17)
Работа силы тяжести ![]() :
:
![]() (23)
(23)
Сумма работ внешних сил определится сложением работ, вычисляемых по формулам (17) – (24):
![]() .
.
Подставляя заданные значения, получаем:
![]()
Или
![]() . (24)
. (24)
Согласно теореме (2) приравняем значения Т и ![]() ,
определяемые по формулам (16) и (24):
,
определяемые по формулам (16) и (24):
![]() ,
,
откуда выводим
![]() м/с.
м/с.
Дано:
R2=30; r2=20; R3=40; r3=40
X=C2t2+C1t+C0
При t=0 x0=7 ![]() =0
=0
t2=2 x2=557 см
X0=2C2t+C1
C0=7
C1=0
557=C2 *52+0*5+7
25C2=557-7=550
C2=22
X=22t2+0t+7
![]() =V=22t
=V=22t
a=![]() =22
=22
V=r2![]() 2
2
R2![]() 2=R3
2=R3![]() 3
3
![]() 3=V*R2/(r2*R3)=(22t)*30/20*40=0,825t
3=V*R2/(r2*R3)=(22t)*30/20*40=0,825t
![]() 3=
3=![]() 3=0,825
3=0,825
Vm=r3*![]() 3=40*(0,825t)=33t
3=40*(0,825t)=33t
atm=r3![]()
![]() =0,825t
=0,825t
atm=R3![]() =40*0,825t=33t
=40*0,825t=33t
anm=R3![]() 23=40*(0,825t)2=40*(0,825(t)2
23=40*(0,825t)2=40*(0,825(t)2
a=![]()
***********************************
Дано :R2=15; r2=10; R3=15; r3=15
X=C2t2+C1t+C0
При t=0 x0=6 ![]() =3
=3
t2=2 x2=80 см
X0=2C2t+C1
C0=10
C1=7
80=C2 *22+3*2+6
4C2=80-6-6=68
C2=17
X=17t2+3t+6
![]() =V=34t+3
=V=34t+3
a=![]() =34
=34
V=r2![]() 2
2
R2![]() 2=R3
2=R3![]() 3
3
![]() 3=V*R2/(r2*R3)=(34t+3)*15/10*15=3,4t+0,3
3=V*R2/(r2*R3)=(34t+3)*15/10*15=3,4t+0,3
![]() 3=
3=![]() 3=3,4
3=3,4
Vm=r3*![]() 3=15*(3,4t+0,3)=51t+4,5
3=15*(3,4t+0,3)=51t+4,5
atm=r3![]()
![]() =3,4t
=3,4t
atm=R3![]() =15*3,4t=51t
=15*3,4t=51t
anm=R3![]() 23=15*(3,4t+0,3)2=15*(3,4(t+0,08)2
23=15*(3,4t+0,3)2=15*(3,4(t+0,08)2
a=![]()
Решение второй задачи механики
Дано:
m=4.5 кг; V0=24 м/с;
R=0.5V H;
t1=3 c;
f=0.2;
Q=9 H; Fx=3sin(2t) H.
Определить: x = f(t) – закон движения груза на участке ВС
Решение:
1) Рассмотрим движение на промежутке АВ

учитывая, что R=0.5V H;
![]()
Разделяем переменные и интегрируем
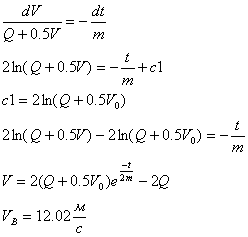
2) Рассмотрим движение на промежутке ВС (V0=VB)
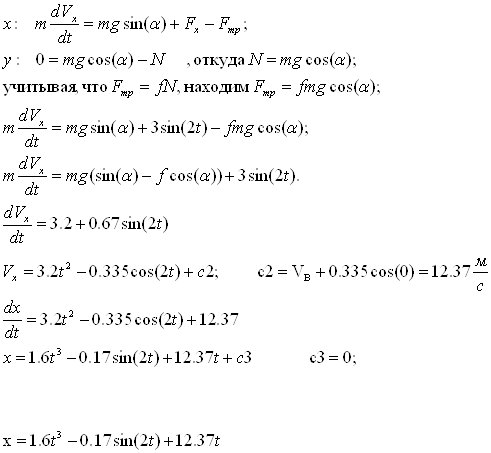
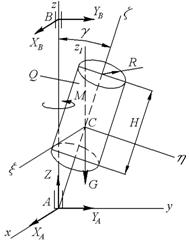
Дано:
m=36 кг
R=6 см=0,06 м
H=42 см=0,42 м
yC=1 см=0,01 м
zС=25 см=0,25 м
АВ=52 см=0,52
М=0,8 Н·м
t1=5 с
Найти реакции в опорах А и В.
Решение
Для решения задачи используем систему уравнений, вытекающую из принципа Даламбера:
 (1)
(1)
Для определения углового ускорения ε из последнего уравнения системы (1) найдем момент инерции тела относительно оси вращения z по формуле
![]() , (2)
, (2)
где Jz1− момент инерции тела относительно центральной оси Сz1, параллельной оси z; d – расстояние между осями z и z1.
Воспользуемся формулой
![]() , (3)
, (3)
где α, b, g - углы, составленные осью z1 с осями x, h, z соответственно.
Так как α=90º, то
![]() . (4)
. (4)
Определим моменты инерции тела ![]() ,
, ![]() как однородного сплошного
цилиндра относительно двух осей симметрии h, z
как однородного сплошного
цилиндра относительно двух осей симметрии h, z
![]() ;
;
![]() .
.
Вычисляем
![]() ;
;
![]() .
.
Определяем угол g из соотношения
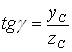 ;
;
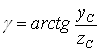 ;
;
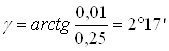 .
.
Угол b равен
![]() ;
;
![]() .
.
По формуле (4), вычисляем
![]() .
.
Момент инерции тела относительно оси вращения z вычисляем по формуле (2):
![]() ,
,
где d=yC;
![]() .
.
Из последнего уравнения системы (1)
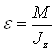 ;
;
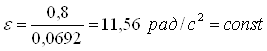 .
.
Угловая скорость при равноускоренном вращении тела
![]() ,
,
поэтому при ω0=0 и t=t1=5 c
![]() .
.
Для определения реакций опор следует
определить центробежные моменты инерции ![]() и
и
![]() тела.
тела. ![]() , так как ось х,
перпендикулярная плоскости материальной симметрии тела, является главной осью
инерции в точке А.
, так как ось х,
перпендикулярная плоскости материальной симметрии тела, является главной осью
инерции в точке А.
Центробежный момент инерции тела ![]() определим по формуле
определим по формуле
![]() ,
,
где ![]() , т.е.
, т.е.
![]() .
.
Тогда
![]() .
.
Подставляя известные величины в систему уравнений (1), получаем следующие равенства
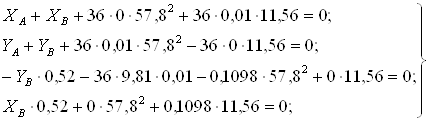
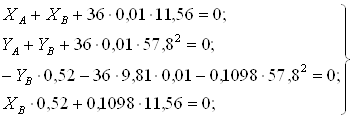
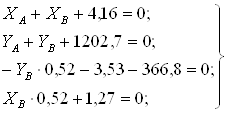
Отсюда
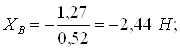
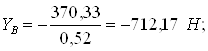
![]()
![]()
Ответ: ![]() ,
,
![]() ,
, ![]() ,
, ![]() .
.
Определение скорости и ускорения точки по заданным уравнениям ее движения
Задание: по заданным уравнениям движения точки М установить вид ее траектории и для момента времени t = t1 (с) найти положение точки на траектории, ее скорость, касательное и нормальное ускорения, а также радиус кривизны траектории.
Исходные данные:
x=5cos(pt2/3); y= -5sin(pt2/3); (1)
t1=1 (x и y – в см, t и t1 – в с).
Решение:
Уравнения движения (1) можно рассматривать как параметрические уравнения траектории точки. Получим уравнения траектории в координатной форме.
x2 + y2 = (5cos(pt2/3))2 + (-5sin(pt2/3))2;
Получаем x2 + y2 = 25, т. е. траекторией точки является окружность, показанная на рис. 1.
Вектор скорости точки
![]() (2)
(2)
Вектор ускорения точки
![]()
Здесь Vx , Vy , ax, ay – проекции скорости и ускорения точки на соответствующие оси координат.
Найдем их, дифференцируя по времени уравнения движения (1)
 (3)
(3)
По найденным проекциям определяем модуль скорости:
V=Ö(Vx2 + Vy2); (4)
и модуль ускорения точки:
а =![]() Ö(ах2 +ау2).
(5)
Ö(ах2 +ау2).
(5)
Модуль касательного ускорения точки
аt=|dV/dt|, (6)
аt= |(Vxax+Vyay)/V| (6’)
Знак “+” при dV/dt означает, что движение точки ускоренное, знак “ - “ - что движение замедленное.
Модуль нормального ускорения точки
ап= V2/p; (7)
p – радиус кривизны траектории.
Модуль нормального ускорения точки можно найти и следующим образом:
an =![]() Ö(а2 -at2); (8)
Ö(а2 -at2); (8)
После того как найдено нормальное ускорение по формуле (8), радиус кривизны траектории в рассматриваемой точке определяется из выражения:
p=V2/ an. (9)
Результаты вычислений по формулам (3)-(6), (8), (9) для момента времени t1=1с приведены ниже в таблице
|
Координаты см |
Скорость см/с |
Ускорение, см/с2 |
Радиус см |
|||||||
| х | у |
Vx |
Vy |
V |
ax |
ay |
a |
at |
an |
p |
| 2.5 | -2.5Ö3 | -5p/Ö3 | -5p/3 | 10p/3 | -20.04 | 13.76 | 24.3 | 10.5 | 21.9 | 5 |
Ниже на рисунке показано положение точки М в заданный момент времени.
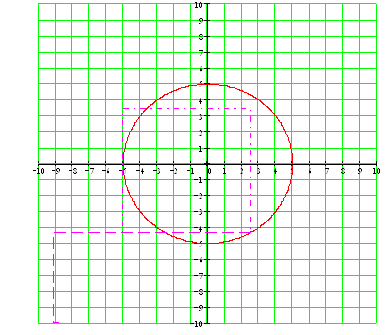
Дополнительное задание:
z=1.5t x=5cos(pt2/3); y= -5sin(pt2/3); t1=1 (x и y – в см, t и t1 – в с).
Найдем скорости и ускорения дифференцируя по времени уравнения движения

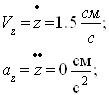
По найденным проекциям определяем модуль скорости:
V=Ö(Vx2 + Vy2+Vz2);
и модуль ускорения точки:
а =![]() Ö(ах2 +ау2+
аz2).
Ö(ах2 +ау2+
аz2).
V=![]() ;
;
a=24.3 см/с;
Касательное ускорение точки
аt= |(Vxax+Vyay+ Vzaz)/V|
at=(-9.069*(-20.04)+(-5.24)*13.76+1.5*0)/10.58=10.36 см/с
Модуль нормального ускорения точки можно найти и следующим образом:
an =![]() Ö(а2 -at2);
Ö(а2 -at2);
an=21.98 см/с2.
Радиус кривизны траектории в рассматриваемой точке определяется из выражения:
p=V2/ an. р=5.1 см
Результаты вычислений для момента времени t1=1с приведены ниже в таблице
Координаты см |
Скорость см/с |
Ускорение, см/с2 |
Радиус см |
||||||||||
| x | y | z |
Vx |
Vy |
Vz |
V |
ax |
ay |
az |
a |
at |
an |
p |
| 2.5 | -4.33 | 1.5 | -9.07 | -5.24 | 1.5 | 10.58 | -20.04 | 13.76 | 0 | 24.3 | 10,36 | 21.98 | 5.1 |
Задание: точка М движется относительно тела D. По заданным уравнениям относительного движения точки М и движения тела D определить для момента времени t=t1 абсолютную скорость и абсолютное ускорение точки М.
Дано:
ОМ=Sr=120pt2 см;
jе=8t2 – 3t рад ;
t1=1/3 c; R=40 см.
Решение:
1) Положение точки М на теле D определяется расстоянием Sr=ОМ
при t=1/3 c Sr=120p/9=41.89 см.
![]()
При t=1/3с Vr=80p=251.33 см/с.
art=d2Sr/dt2 art=240p=753.98 см/с2
arn=Vr2/R arn=(80p)2/40=1579.14 см/с2
2) Ve=wer , где r- радиус окружности, описываемой той точкой тела, с которой в данный момент совпадает точка М.
a=OM/R. r=R*sina=40*sin(p/3)=34.64 см.
wе=dje/dt=16t-3 при t=1/3 wе=7/3=2.33 с-1
Ve=80.83 см/с.
аец=we2 r аец=188.6 см/с2.
аев=eеr eе= d2je/dt2=16 с-2 аев=554.24 см/с2.
3) ![]()
ас=2*wеVrsin(wе, Vr) sin(wе, Vr)=90-a=p/6 ac=585.60 см/с2
4) 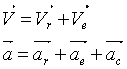
V=Ö(Ve2+Vr2) V=264.01 см/с
Модуль абсолютного ускорения находим методом проекций.
ax=aев+ас
ay=arncos(p/3)+artcos(p/6)
az=-аец - arncos(p/6)+artcos(p/3)
а=Ö(ax2+ay2+az2)
Результаты расчетов сведены в таблицу
|
we, c-1 |
Скорость см/с |
eе с-2 |
Ускорение , см/с2 |
||||||||||
|
Ve |
Vr |
V |
аец |
aев |
arn |
аrt |
ас |
ax |
ay |
az |
а |
||
| 2.33 | 80.8 | 251.3 | 264 | 16 | 188.6 | 554 | 1579 | 754 | 586 | 1140 | 1143 | -1179 | 1999 |
Определение реакций опор твердого тела
Дано:
Q=10 kH;
G=5 kH;
a=40 см; b=30 см; c=20 см;
R=25 см; r=15 см.
Задание:
Найти реакции опор конструкции.
Решение:
Для определения неизвестных реакций составим уравнения равновесия.

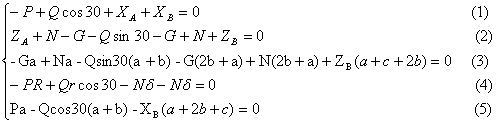
Из уравнения (4) определяем P, а затем находим остальные реакции опор. Результаты вычислений сведем в таблицу.
Силы, кНР |
ХА |
ZA |
XB |
ZB |
| 5.15 | -0.17 | 2.08 | -3.34 | 2.92 |
Проверка.
Составим уравнения относительно точки В.