Контрольная работа: Основы тепломассообмена
1. Стационарная передача через плоскую стенку
Теплота дымовых газов передаётся через стенку воде. Принимая температуру газов tж1, воды tж2, коэффициент теплоотдачи газами стенки α1 и от стенки воде α2 и считая стенку плоской, требуется:
1. Подсчитать термические сопротивления, коэффициенты теплопередачи и количество передаваемой теплоты от газов к воде через 1м2 стенки для следующих случаев:
а) стенка стальная совершенно чистая, толщиной δ2 (λ2=50 Вт/(м·ºС);
б) стенка стальная, со стороны воды покрыта слоем накипи толщиной δ3 (λ3=2 Вт/(м·ºС);
в) стенка стальная, со стороны газов покрыта слоем сажи толщиной δ1=2 мм (λ1=0,2 Вт/(м·ºС);
г) стенка стальная, со стороны воды покрыта слоем накипи толщиной δ3, а со стороны газов – сажей толщиной δ1.
2. Определить температуры всех слоев стенки для случая г.
3. Построить в масштабе линию падения температуры в стенке для случая г.
Дано: tж1=950ºС, tж2=210ºС, α1=65 Вт/(м2·ºС), α2·10-3=2,1 Вт/(м2·ºС), δ2=19 мм, δ3=5 мм.
Термическое сопротивление теплопередаче:
![]()
![]()
![]()
![]()
Коэффициенты теплопередачи
![]()
![]()
![]()
![]()
Количество передаваемой теплоты от газов к воде через 1 м2 стенки определим из уравнения теплопередачи:
![]()
![]()
![]()
![]()
![]()
Температуры всех слоев стенки для случая г.
Плотность теплового потока от газов к стенке
![]()
отсюда ![]()
Плотность теплового пока через слой сажи
![]()
Отсюда ![]()
Плотность теплового потока через стальную стенку
![]()
Отсюда ![]()
Плотность теплового потока через слой накипи
![]()
Отсюда ![]()
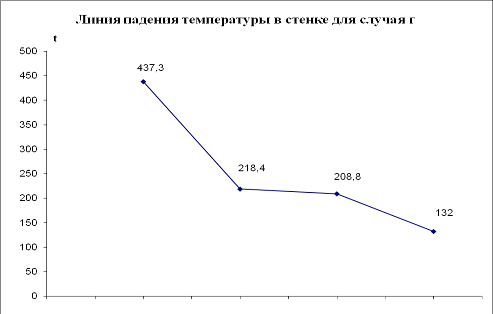
2. Расчет тепловой изоляции
Стальная труба (λтр) внутренним диаметром d с толщиной стенки δ1 покрыта слоем изоляции, коэффициент теплопроводности которой λиз. По трубе протекает вода, температура которой tж1. Коэффициент теплоотдачи воды к стенке α1. Снаружи труба омывается свободным потоком воздуха, температура которого tж2=20ºС; коэффициент теплоотдачи к воздуху α2 =10 Вт/(м2·ºС);
Требуется:
1. Найти толщину изоляционного материала, обеспечивающую температуру наружной поверхности изоляции 60ºС.
2. Сопоставить тепловые потоки через трубу с изоляцией и без неё при тех же tж1, tж2, α1 и α2.
3. Дано: d=66 мм; tж1=250°С; α110-3=1,7 Вт/(м2°С); λиз=0,08 Вт/(м2°С); λтр=48Вт/(м2°С).
Линейная плотность теплового потока через изолированную трубу

Линейная плотность теплового потока от изоляции к наружному воздуху
![]()
Приравниваем правые части этих уравнений и представим решение в виде
![]()
Где
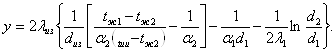
Подставим значение соответствующих величин и получим
![]()
Для
графического решения полученного уравнения зададимся значениями dиз, определим y и ![]() , а полученные результаты
представим в таблице:
, а полученные результаты
представим в таблице:
|
dиз |
0,082 | 0,092 | 0,102 | 0,112 | 0,122 | 0,132 | 0,142 |
|
dиз/ d2 |
1,139 | 1,278 | 1,417 | 1,556 | 1,694 | 1,833 | 1,972 |
|
|
0,130 | 0,245 | 0,348 | 0,442 | 0,527 | 0,606 | 0,679 |
|
y |
0,925 | 0,824 | 0,743 | 0,677 | 0,621 | 0,574 | 0,533 |
![]()
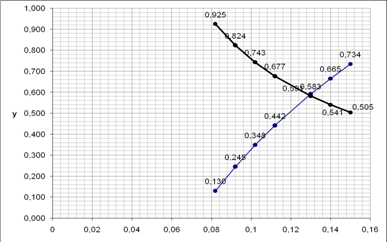
Полученные
данные наносим на график и получаем значение корня dиз=0,129 м, которое
удовлетворяет уравнению ![]()
Линейная плотность теплового потока через изолированную трубу

Линейная плотность теплового потока неизолированного трубопровода
 =515,5
=515,5
Следовательно, у неизолированного трубопровода потери теплоты с 1 м в 3,2 раза больше, чем у изолированного.
3. Нестационарный нагрев длинного круглого вала
Длинный стальной вал диаметром D с начальной температурой tо=20ºС помещен в печь, температура в которой tж. Суммарный коэффициент теплоотдачи к поверхности вала α.
Определить:
1. Время τ1, необходимое для нагрева вала, если нагрев считается законченным, когда температура на оси вала tr=0=tж-20ºС.
2. Значение температуры на поверхности вала tr=R в конце нагрева.
3. Значение температур на поверхности и оси вала через τ2=(0,2; 0,4; 0,6; 0,8) · τ1 после начала нагрева.
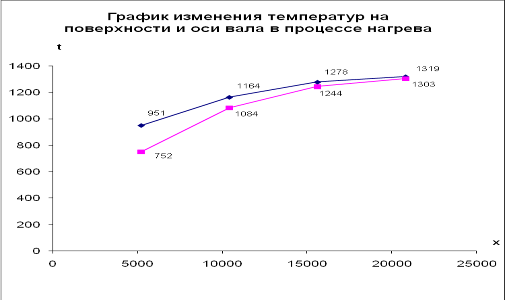
4. Построить в масштабе график изменения температур на поверхности и оси вала в процессе нагрева.
Дано: D=750 мм; tж=1350°С; α=155 Вт/(м2°С)
1. Температуру на оси и на поверхности вала при его нагреве в среде с постоянной tж будем определять с помощью номограмм.
По известным значениям радиуса и коэффициента α найдем значения критерия Био
![]()
![]()
По номограмме F0=2,3
2. Безразмерную температуру на поверхности вала найдем из номограммы на стр. 257
![]()
![]()
|
τ2 |
0,2τ1 |
0,4τ1 |
0,6τ1 |
0,8τ1 |
|
τ2, с |
5200 | 10400 | 15600 | 20800 |
|
|
0,46 | 0,92 | 1,39 | 1,85 |
|
Θr=R |
0,3 | 0,14 | 0,054 | 0,023 |
|
tr=R,°C |
951 | 1164 | 1278 | 1319 |
|
Θr=0 |
0,45 | 0,2 | 0,08 | 0,035 |
|
tr=0 |
752 | 1084 | 1244 | 1303 |
4. Сложный теплообмен
Паропровод наружным диаметром d, мм, расположен в большом помещении с температурой воздуха tж, ºС. Температура поверхности паропровода tс1, ºС. Определить тепловые потери с единицы длины паропровода за счет излучения и конвекции и сравнить их. Приведенная степень черноты поверхности εпр. Температуру стен помещения принять равной температуре воздуха, т.е. tс2=tж.
Дано: d=320 мм, tж=29 ºС, εпр=0,8, tс1=300 ºС.
Решение:
Тепловые потери излучением:
![]()
Тепловые потери конвекцией
![]()
Для определения коэффициента теплоотдачи конвекцией используем критериальное уравнение
![]()
При tж=29ºС из таблиц находим Prж=0,7012; λж=2,66·10-2Вт/(м·ºС); υж=15,91·10-6 м2/с.
Значение
Nuж=0,47·(![]() ·106)0,25=84
·106)0,25=84
Средний коэффициент теплоотдачи
![]()
Тепловые потери конвекцией
![]()
Следовательно, потери теплоты излучением 4,5/1,91=2,4 раза больше, чем конвекцией.