Учебное пособие: Понятие устойчивости
Реферат
По физике
УСТОЙЧИВОСТЬ
Лекция 14.
Будем называть равновесное состояние устойчивым, если оно мало изменяется при малых возмущениях.
Приведём некоторые примеры.
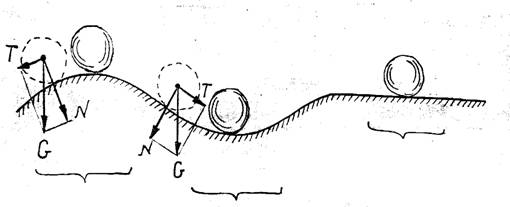
1. Тяжелый шар на поверхности, имеющей вершины, впадины и горизонтальные участки.
|
|
В том случае, когда шарик находится на вершине, составляющая силы тяжести Т, возникающая при его отклонении, уводит его от первоначального состояния, для шарика, находящегося во впадине сила Т будет возвращать отклонённый шарик в первоначальное состояние и он будет колебаться в окрестности наиболее низкой точки впадины, т.е. при малых отклонениях состояние шарика будет также меняться мало. Случай шарика, находящегося на горизонтальной поверхности, будет случаем разграничивающим рассмотренные выше не устойчивые и устойчивые равновесные состояния. Такое состояние называется безразличным.
2. Хорошо знакомую картину разрушение образца при растяжении с образованием шейки можно трактовать, как потерю устойчивости цилиндрической формы образца.
По мере приближения состояния образца становится неустойчивой, образуется шейка и малым изменениям силы соответствуют значительные изменения конфигурации системы.

Рис. 98
3. Центрально сжатый гибкий стержень
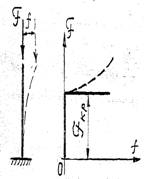
Предполагается, что стержень идеально прямой, а сила прилаженная строго по оси (что, конечно, практически невозможно).
Для того, чтобы судить устойчиво ли данное равновесное состояние, надо приложить горизонтальную возмущающую силу, которая вызовет прогиб. Если сила Р невелика, то прогиб окажется малым, равновесное состояние (прямолинейное) фактически не изменится . Однако если сила Р превысит некоторое значение называется критическим (F кр ), то равновесное состояние становится неустойчивым, т. е. любые малые возмущения приведут к значительным прогибам. Зависимость между прогибом и силой показана действительное поведение стержня, которое можно обнаружить с помощью нелинейных решений, сплошной чертой показано грубое, линейное решение задачи.
Задача Эйлера
Рассмотрим центрально сжатый шарнирно закрепленный с обоих концов стержень. Эта задача была решена Л. Эйлером.
Существо задачи состоит в том, что задача об устойчивости по отношению к заданному возмущению подменяется задачей о возможности существования двух различных форм равновесия при одном и том же значении силы F. Очевидно, что прямолинейная равновесная форма возможна (y = 0). Допустим, что наряду с прямолинейной равновесной формой возможна и криволинейная равновесная форма, показанная на рисунке.
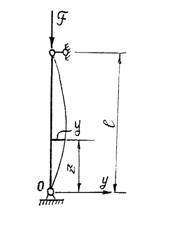
Кривизна стержня на
основании закономерности известной из теории изгиба выразится 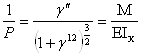
Будем полагать, что угол поворота y’ – величина малая по сравнению с единицей и тем более мал квадрат этой величины по сравнению с единицей
![]()
Изгибающий момент в
произвольном сечении с координатой Z: ![]() (знак минус увязывает
прогиба и кривизны).
(знак минус увязывает
прогиба и кривизны).
Дифференциальное уравнение изогнутой оси выглядит
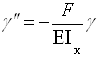 или
или ![]()
![]() (1)
(1)
Решение этого дифференциального уравнения хорошо известно
![]()
Из граничных условий попробуем найти произвольные постоянные
C1 и С2
1)
при Z=0: ![]()
2)
при Z=![]() :
: ![]()
Возможны две ситуации
C1=0, откуда y![]() 0, т. е. получаем прямолинейную
равновесную форму,
0, т. е. получаем прямолинейную
равновесную форму,
Sin K![]() (n
(n![]() N) подставим в (1) выражение R2 =
N) подставим в (1) выражение R2 =
![]()
![]() откуда найдем значение силы, при
которой помимо прямолинейной равновесной формы появляется смежная криволинейная
равновесная форма
откуда найдем значение силы, при
которой помимо прямолинейной равновесной формы появляется смежная криволинейная
равновесная форма
![]()
реальный смысл имеет наименьшее значение силы при n=1 эйлерова сила – критическая сила.
Fкр=![]()
![]()
Очевидно, что Ix – минимальный момент инерции.
Потери устойчивости будет
происходить по синусоиде y = C1Sin![]()
однако произвольную C1 мы так и не смогли найти.
Дело в том, что задача о потере устойчивости задача существенно нелинейно, а мы поступили непоследовательно. С одной стороны мы подошли к задаче как нелинейной, отойдя от принципа начальных размеров, и определив изгибающий момент с учетом изгиба стержня. С другой стороны, приняв приближенное выражение для кривизны, мы линеаризовали задачу. Для того, чтобы определить прогибы в закритической стадии надо исходить из нелинейного дифференциального уравнения.
Однако главная цель – определение критической силы для стержня нами достигнута.
Влияние условий закрепления концов стержня на величину критической силы
Формула (2) даёт возможность определить критическую силу только в том случае шарнирного опирания обоих концов стержня. Обобщим полученный результат на некоторые другие часто встречающиеся случаи закрепления.
а). Стержень, закреплённый жёстко одним концом и свободный от закрепления на другом. Очевидно изгиб стержня в этом случае будет таким же, как и в случае шарнирно опертого стержня, но имеющего длину в 2 раза большую.
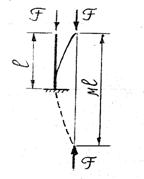
Критическая сила в этом случае
будет равна критической силе шарнирно опёртого стержня, имеющего длину 2![]() .
.
Введём понятие
коэффициента привидения длины - ![]() , т. е.
числа показывающего во сколько раз нужно увеличить длину шарнирно опёртого
стержня, чтобы критическая сила для него равнялась критической силе стержня
длиной
, т. е.
числа показывающего во сколько раз нужно увеличить длину шарнирно опёртого
стержня, чтобы критическая сила для него равнялась критической силе стержня
длиной ![]() при заданном закреплении.
при заданном закреплении.
Очевидно, что в нашем
случае коэффициент ![]() можно трактовать
, как число показывающее сколько раз длина стержня укладывается в длине
полуволны синусоиды, по которой происходит потеря устойчивости.
можно трактовать
, как число показывающее сколько раз длина стержня укладывается в длине
полуволны синусоиды, по которой происходит потеря устойчивости.
Обобщим формулу Эйлера
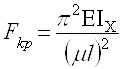 (3)
(3)
Для некоторых других случаев закрепления коэффициент приведения длины равен:
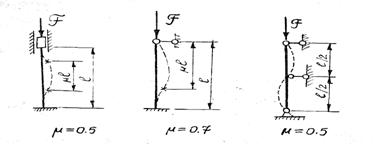
Рис. 102
Пределы применимости формулы Эйлера
Формула Эйлера выведена в предположении, что материал линейно упруг, и, естественно, применила, в тех случаях пока справедлив закон Гука.
Придадим формуле (3) иной вид.
Введём понятие критического напряжения, т. е. напряжения соответствующего критической силе.
![]() ;
; ![]() (4)
(4)
но ![]() где
где ![]() - минимальный радиус
инерции сечения.
- минимальный радиус
инерции сечения.
Введём ещё одну величину – гибкость стержня.
![]() , тогда
, тогда ![]()
Тогда можно оказать, что формула Эйлера справедлива, если критические напряжения не превышают предела пропорциональности при сжатии.
![]()
Выясним при каких гибкостях можно использовать формулу Эйлера .
Приравняем в (4)
![]() =
=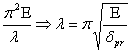
Если ![]() , то можно использовать
формулу (3)
, то можно использовать
формулу (3)
Для малоуглеродистых
сталей, особенно часто используемых для сжатых элементов: ![]() МПа, E = 2*105 МПа
тогда,
МПа, E = 2*105 МПа
тогда,
![]() т.е. для малоуглеродистых сталей формулу Эйлера можно
использовать при гибкостях больших 100.
т.е. для малоуглеродистых сталей формулу Эйлера можно
использовать при гибкостях больших 100.
Коэффициент запаса на устойчивость
Представляет собой отношение критической силы для стержня к силе, действующей на него.
![]()
Коэффициент запаса на
устойчивость может выступать, некоторая заданная нормативная величина, тогда 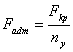 ,где
,где ![]() Fadm – нагрузка допускаемая из условия
устойчивости.
Fadm – нагрузка допускаемая из условия
устойчивости.
Пример.
Для заданного сжатого стержня определить допускаемую силу
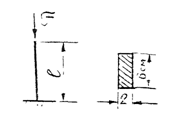
![]() = 50 см; материал Ст. 3
= 50 см; материал Ст. 3
E = 2 105 МПа; ![]() = 210 МПа
= 210 МПа
ny= 2
Ix = Imin = 4 см2 ; A = 2*6 = 12 см2;
![]()
![]() = 2*50 = 100 см;
= 2*50 = 100 см;
Fkp =
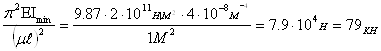
 МПа;
МПа; ![]() kp
kp![]() МПа
МПа![]() МПа
МПа![]() pr
pr
формула Эйлера применима
Fadm = 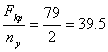 кН
кН
Расчет сжатых стержней на устойчивость по коэффициенту снижения допускаемых напряжений
Приведенное выше решение пригодно только для сравнительно длинных и тонких стержней. В случае коротких и жестких стержней потеря устойчивости происходит при возникновении пластических деформаций и задача требует специального рассмотрения. Существует решения (Т. Карман, Энгессер) об устойчивости стержня за пределами упругости. Иногда прибегают к эмпирическим формулам типа формулы Ясинского.
![]() , где a и b-константы зависящие от
свойств материала.
, где a и b-константы зависящие от
свойств материала.
Изложим методику расчёта на устойчивость, предложенную русским инженером Ясинского в конце прошлого века. Суть этой методики состоит в том, что расчёт на устойчивость подменяется расчетом на обыкновенное сжатие, но допускаемые напряжения при этом полагаются переменными, зависящими от гибкости. Допускаемое напряжение на устойчивость полагается равным
![]()
![]() - допускаемое напряжение при сжатии;
- допускаемое напряжение при сжатии;
![]() - коэффициент снижения допускаемых
напряжений. Он может трактоваться, как следующее отношение.
- коэффициент снижения допускаемых
напряжений. Он может трактоваться, как следующее отношение.
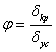
Коэффициент снижение
допускаемых напряжений зависит от гибкости ![]()
С увеличением гибкости величины его уменьшается.
Разумеется, что![]() зависит не только от
гибкости, но и от свойств материала. Для наиболее употребительных материалов он
вычислен и приведён в таблицах. Приведем такую таблицу для ст. 3 материала
наиболее часто применяемого для сжатых элементов.
зависит не только от
гибкости, но и от свойств материала. Для наиболее употребительных материалов он
вычислен и приведён в таблицах. Приведем такую таблицу для ст. 3 материала
наиболее часто применяемого для сжатых элементов.
|
|
|
|
|
| 0 | 1,00 | 110 | 0,52 |
| 10 | 0,99 | 120 | 0,45 |
| 20 | 0,96 | 130 | 0,40 |
| 30 | 0,94 | 140 | 0,36 |
| 40 | 0,92 | 150 | 0,32 |
| 50 | 0,89 | 160 | 0,29 |
| 60 | 0,86 | 170 | 0,26 |
| 70 | 0,81 | 180 | 0,23 |
| 80 | 0,75 | 190 | 0,21 |
| 90 | 0,69 | 200 | 0,19 |
| 100 | 0,60 | --- | --- |
Для промежуточных
значений ![]() соответствующие значения
определяются путем линейной интерполяции.
соответствующие значения
определяются путем линейной интерполяции.
Примеры.
Если известно сечение сжатого элемента, то нагрузку которую может воспринять стержень из условия устойчивости определяется.
Nadm = ![]()
![]()
1. Определить величину допускаемой нагрузки на ферму из условия устойчивости поясов АВ и ВД.
Материал – Ст. 3, ![]() = 160МПа
= 160МПа
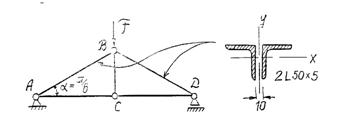
Рис. 104
Площадь сечения А = 2АL = 2*4,8 = 9,6 см2 ;
Минимальный момент инерции сечения будет
Ix = 2ILx
Минимальный радиус инерции
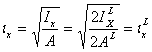
По сортаменту определяем ![]() =1,53см
=1,53см
Приведенная длина верхнего пояса
![]()
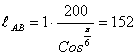 см
см
Гибкость ![]()
![]() по таблице
по таблице
Допускаемое усилие из условия устойчивости для стержня AB:
![]()
![]()
Свяжем между собой силу, действующую на ферму F и усилие NAB
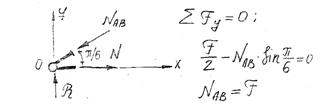
Рис. 105
Допускаемая нагрузка на ферму
Fadm=48.5кн
Другим типом задачи является подбор размером сечения заданного типа. Можно записать
A=![]()
Однако ![]() зависит от размеров и формы сечения,
таким образом круг замыкается и задача может быть решена только методом
попыток. По сути задача подбора сечения сводится к некоторой последовательности
задач первого типа.
зависит от размеров и формы сечения,
таким образом круг замыкается и задача может быть решена только методом
попыток. По сути задача подбора сечения сводится к некоторой последовательности
задач первого типа.
2. Подобрать размеры квадратного
поперечного сечения для сжатого стержня. F=280кн. Материал Ст.3 ![]() =160МПа:
=160МПа:
![]() =1м. Разберемся с
геометрическими характеристиками
=1м. Разберемся с
геометрическими характеристиками
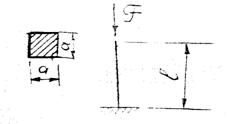
Рис. 106
A=a2
; Ix=![]() ;
; ![]()
1) ![]()
![]() см
см
a=![]() см;
см; ![]() см2;
см2;
Нагрузка, которую может воспринять сечение при заданных размерах
![]()
Размеры сечения слишком велики
2)![]()
![]() см
см
a=![]() см;
A=24см2;
см;
A=24см2;
![]()
Размеры сечения слишком малы
3)
Т. к. в обоих
случаях мы оказались далеки от истины, то попробуем в качестве следующего
значения ![]() среднее арифметическое из
первых двух
среднее арифметическое из
первых двух
![]()
![]()
![]() см; a =
см; a =![]() см; A=36см2;
см; A=36см2;
![]() кн
кн
Обычно считается, что результат достигнут, если сила, которую воспринимает сечение отличается от действующей силы не более чем на 5% в ту или другую сторону т. е.
0,95F ![]()
В нашем случае это условие выполнено.
Принимает размер сечения a = 6см
Лекция 15
Энергетический способ определения критических сил
В сколь-нибуть сложных случаях, получить критическую силу из решения дифференциального уравнения изогнутой оси сжатого стержня затруднительно.
Поэтому в подобной ситуации проще получить приближённое решение, например, энергетическим методом.
Рассмотрим стержень центрально сжатый силой F. Условно на рисунке стержень показан шарнирно опёртым, но вопрос о граничных условиях пока оставим открытым
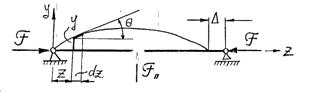
Рис. 106
Пусть сила F меньше эйлеровой критической силы. Если приложить к стержню некоторую поперечную нагрузку Fп, то стержень изогнётся, но будет находиться в устойчивом равновесном состоянии. Сжимающая сила совершит при этом работу на перемещении ▲, которое можно найти следующим образом.
Укорочение малого элемента длиной dz будет равно
![]() ▲=
▲= ![]()
учтём, что ![]() = y'
= y'
Тогда ▲=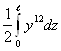
Потенциальная энергия деформации изогнутого стержня
U=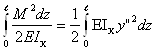
Здесь учтено, что M = EIxy”
Изменение полной энергии при малом изгибе будет
![]()
Если ![]() , то стержень устойчив,
если же
, то стержень устойчив,
если же ![]() , т.е. F
, т.е. F![]() производит работу большую, чем может
на копиться в стержне в виде энергии упругой деформации, избыточная работа идёт
на сообщение кинетической энергии, стержень приходит в движение и прогибается
дальше. Т.е. он не устойчив. Очевидно, что когда сила достигает критического
значения, то Fкр
производит работу большую, чем может
на копиться в стержне в виде энергии упругой деформации, избыточная работа идёт
на сообщение кинетической энергии, стержень приходит в движение и прогибается
дальше. Т.е. он не устойчив. Очевидно, что когда сила достигает критического
значения, то Fкр![]() или
или
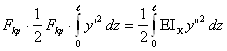 откуда
откуда
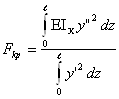
Для получения значения критической силы необходимо задаться формой изогнутой оси. Функцию y = y(z) надо подбирать таким образом, чтобы она удовлетворяла граничным условиям.
Примеры
1) Вначале попробуем решить рассмотренную ранее задачу о критической силе для шарнирно опёртого по обоим концам стержня. Точное решение известно.
Fkp =
![]()
Форма изогнутой оси в этом случае известна
y = CSin![]()
но предположим, что это нам не известно и аппроксимируем изогнутую ось полиномом четвёртой степени
![]()
Граничные условия следующие
А) при Z = 0: y=0 (1) ; y”=0 (2) прогиб равен нулю и момент равен нулю,
Б) при Z = ![]() : y = 0 (3) ;y”=0 (4)
: y = 0 (3) ;y”=0 (4)
Возьмём производные
y’ = 4Az3+3Bz2+2Cz+D;
y” = 12 Az2+6Bz+2C
Из (1) E = 0 ; bp (2) C = 0
Используем (3) ![]() ; из (4) следует
; из (4) следует
12 A![]() подставляя в (3): A
подставляя в (3): A![]()
D=A![]() y’=A(4z3-6
y’=A(4z3-6![]() ; y”=12A(z2-
; y”=12A(z2-![]()
Подставим эти выражения в формулу (1)
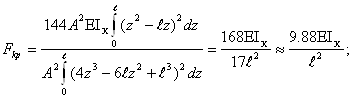
Как видим, приближённое решение практически не отличается от точного.
2)Рассмотрим более сложную задачу.
Определить критическую силу для стержня , показанного на рисунке.
Аналогично предыдущему случаю, аппроксимируем изогнутую ось полиномом
y = Az4+Bz3 +Cz2 +Dz+E
Запишем граничные условия
1) при z = 0 y = 0 (1)
y’ = 0 (2)
2) при z =3![]() :
y” = 0 (свободный конец и момент
отсутствует) (4)
:
y” = 0 (свободный конец и момент
отсутствует) (4)
Найдем производные
y' = 4Az3+3Bz2+2Cz+D
y” = 12Az2+6Bz+2C;
Используем граничные условия
Из (1) E = 0 ; из (2) D = 0
Из (3) A16![]() 4+B8
4+B8![]() 3+C4
3+C4![]() =0
=0
4![]() 2A+2
2A+2![]() B+C=0 (3а)
B+C=0 (3а)
Из (4) 12A*9![]() 2+6B*3
2+6B*3![]() +2C=0
+2C=0
54![]() 2A+9
2A+9![]() B+C=0 (4а)
B+C=0 (4а)
Решим совместно (3а) и (4а)
_9![]() B+C=-54
B+C=-54![]() 2A
2A
2![]() B+C=-4
B+C=-4![]() 2A
2A
------------------------
7![]() B=-50
B=-50![]() 2A B=
2A B=![]() ;
;
C=-4![]() 2-2
2-2![]() (
( ![]() )=
)=![]()
Подставим найденные значения коэффициентов полинома в выражения для
y’=2A(2z3-![]()
![]() z2+
z2+![]() )
)
y” = 12A(z2-![]()
![]() z+
z+![]() .
.
Подставим в (1)

Вычисляя интеграл, получаем
Fkp![]()