Курсовая работа: Расчет параметров вентильного электропривода
Министерство общего и профессионального образования РФ
Саратовский государственный технический университет
Кафедра "Приборостроение "
Расчет параметров вентильного электропривода
Пояснительная записка к курсовой работе
по курсу "Электрический привод"
Выполнила:
студентка
Проверил :
Здражевский Р.А.
Саратов 2005
Содержание
Исходные данные для выполнения курсовой работы
1. Принцип действия вентильного электропривода
2. Вывод математической модели ВЭП
3. Расчет устойчивости
4. Математическое моделирование ВЭП
5. Построение АЧХ и ФЧХ ВЭП
6. Расчет суммарного момента возмущения
Заключение
Исходные данные для выполнения курсовой работы
Вариант №5
| См | Се | J | Кос | Кт | Lэ |
Кi |
Tω |
Т1 |
Rэ |
МКS |
МКС |
| Нм/А | Вс/рад |
Кг*м2 |
Вс/рад | Ом | Гн | сек | сек | Ом | Нм | Нм | |
| 0, 205 | 0, 205 | 8,00E-05 | 2,30E-02 | 0,27 | 6,50E-04 | 1,3 | 1,52E-03 | 2,80E-03 | 0,52 | 5,40E-03 | 2, 20E-03 |
1. Принцип действия вентильного электропривода
При протекании тока в рамке (см. рис.2) возникает вращающий момент:
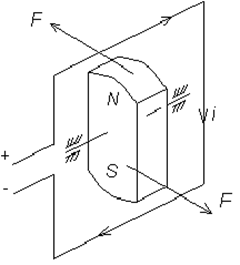
Рис.1 Формирование вращающего момента.
![]() (1)
(1)
где: В - магнитная индукция, Тл; S-площадь рамки, см2; W-число витков рамки; i-ток, А; a-угол между намагничивающей силой и рамкой с током.
Этот момент повернет ротор (постоянный магнит) на 90°. В вентильном электродвигателе в статоре расположено 3 обмотки и в зависимости от положения ротора относительно статора подключаются 2 обмотки, скорость и момент определяются питающим напряжением. При постоянном питающем напряжении скорость вращения постоянна. Управление подключением обмоток осуществляется транзисторной схемой переключения (рис.3), сигналы на которую поступают с датчика положения ротора. Если условно принять за положительное напряжение вращения вала направление вращения против часовой стрелки, то момент на валу двигателя будет определяться по формуле:
![]()
где: q-угол между векторами Ф0 и F; Mmax=Ф0·F; К= 1/ 9810.
Наибольшее значение момента двигателя достигается при = 90°+30°
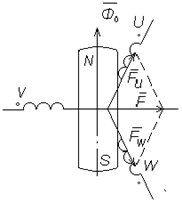
Рис 2. Формирование результирующей намагничивающей силы.
Система автоматического управления (САУ) (рис.3), управляемая датчиком положения ротора, обеспечивает одновременное открытие транзисторных ключей, одного из группы VT1-VT3 и другого из группы TV4-VT6, что обеспечивает в свою очередь одновременное включение двух статорных обмоток двигателя.
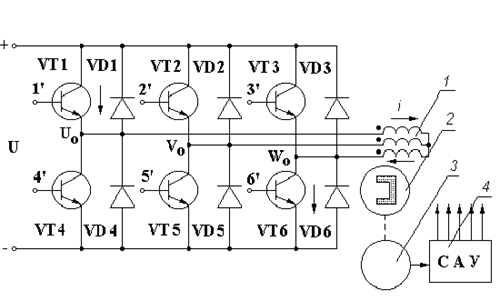
Рис 3. ВЭП. Схема электрическая функциональная.
На рис.4 приведена типовая электрическая схема переключения полюсов вентильного электропривода, где: 1-статорные обмотки ВЭП; 2-ротор двигателя; 3 - ДПД; 4 - САУ.
Рассмотрим работу ВЭП, когда например, открыты транзисторы VT1 и VT6 (рис 4). Тогда ток от источника U будет протекать через эти транзисторы и обмотки двигателя U и W. При этом создается результирующая намагничивающая сила F, которая при взаимодействии с магнитным потоком постоянных магнитов ротора Ф0 создает вращающий момент, величина которого определяется углом рассогласования между векторами Ф0 и F.
2. Вывод математической модели ВЭП
На рис.4 изображена структурная схема ВЭП, где приняты следующие обозначения: 1-сумматор напряжений (устройство суммирования построено на ОУ); 2-передаточная функция регулятора скорости, которая является суммой форсирующего 1-го порядка и интегрирующего элементов (е1 и е2 - напряжения на входе и выходе регулятора); 3-сумматор напряжений; 4-усилитель мощности на транзисторах и тиристорах; 5-сумматор напряжений (обмотка статора); 6-передаточная функция обмотки статора (Rэ - активное сопротивление обмотки, Т - постоянная времени обмотки, Lэ - индуктивность обмотки); 7-усилитель тока; 8-передаточная функция электромагнитной части электродвигателя, в которой реализуется закон Ампера, т.е. ток преобразуется в силу (Сm - постоянная по моменту, Се - постоянная по ЭДС); 9-передаточная функция по ЭДС электродвигателя; 10-сумматор моментов - ротор электродвигателя (Мт - момент трения; Мр - реактивный момент); 11-передаточная функция механической части электропривода (J - приведенный момент инерции электропривода); 12 - обратная связь по угловой скорости ( (в качестве измерителя угловой скорости выступает тахогенератор, закрепленный на валу электродвигателя, который позволяет стабилизировать заданное значение угловой скорости на выходе электропривода); 13 - интегрирующее звено; 14-наблюдающее устройство идентификации (НУИ).
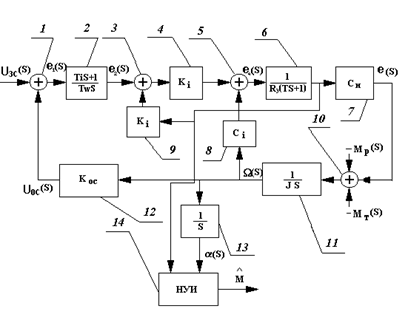
Рис 5. Структурная схема ВЭП.
На основе данной схемы можно получить уравнения описывающие поведение ВЭП:
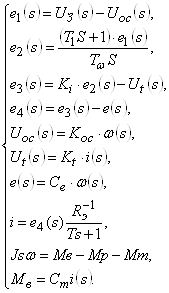 (2)
(2)
Записывая характеристическое уравнение системы (2) можно получить уравнения, которые характеризуют динамику тока в обмотках ВЭП и динамику скорости вращения его вала. Эти уравнения соответственно имеют вид:
![]() (3)
(3)
![]() (4)
(4)
где приняты следующие обозначения:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Таким образом динамика ВЭП описывается двумя линейными дифференциальными уравнениями третьего порядка (3), (4). В качестве переменных состояния выступают частота вращения w вала двигателя и ток в обмотках i. В качестве управляющего воздействия выступает напряжение питания Uз, а в качестве возмущающего воздействия - момент трения и реактивный момент.
Для заданных параметров ВЭП коэффициенты уравнений (3), (4) будут иметь следующие значения:
| a1 | a2 | a3 | | | 1 |
| 1,32E-02 | 1,73E-05 | 1,29E-08 | 7,46E-04 | 2,16E-01 | 1,32E-02 |
3. Расчет устойчивости
Для исследования устойчивости ВЭП по соответствующей математической модели воспользуемся алгебраическим критерием устойчивости в форме определителей составляемых из коэффициентов характеристического уравнения (критерий устойчивости Гурвица). Критерий устойчивости формулируется следующим образом: для того чтобы система была устойчива, необходимо и достаточно, чтобы все определители Гурвица имели знаки, одинаковые со знаком первого коэффициента характеристического уравнения.
Для характеристического уравнения третьего порядка условия устойчивости будут иметь вид:
D1=а2>0;
D2=а2·а1-а3>0;
D3=а2·а1-а3>0;
В нашем случае условия устойчивости выполняются, следовательно, система характеризующая динамику ВЭП, описываемая уравнениями (3-4) является асимптотически устойчивой.
4. Математическое моделирование ВЭП
Математическое моделирование производилось при помощи математического редактора MatLab 6.12 с использованием приложения для построения и моделирования динамических систем Simulink по структурной схеме.
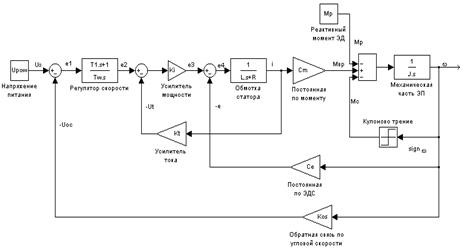
Рис.6 Структурная схема ВЭП для моделирования в среде MatLab 6.12
Результаты моделирования приведены на рис.7-8.
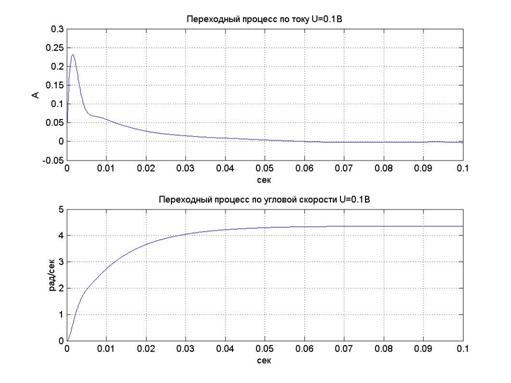
а)
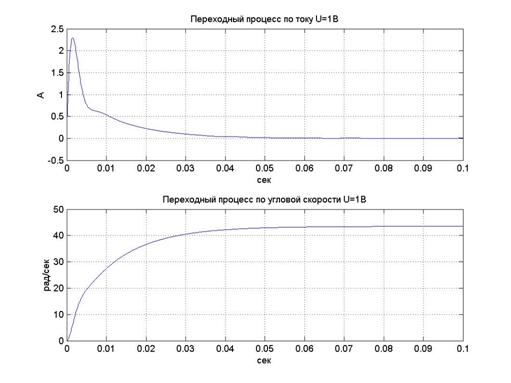
б)
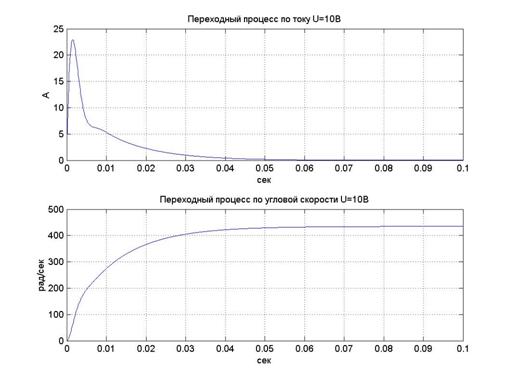
с)
Рис.7 Результаты моделирования переходных процессов по угловой скорости и по току для различных напряжений питания ВЭП: а) 0.1В (tпп 0,05 сек); б) 1В (tпп 0,05 сек); с) 10В (tпп 0,05 сек).
5. Построение АЧХ и ФЧХ ВЭП
Выражения (3) и (4) можно записать в изображениях Лапласа в виде:
![]() (5)
(5)
![]() (6)
(6)
где W1 (s), W2 (s), W3 (s), W4 (s) - передаточные функции ВЭП по w для управления и возмущения, и соответственно по i для управления и возмущения, которые имеют вид:
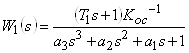 (7)
(7)
![]() (8)
(8)
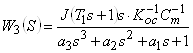 (9)
(9)
 (10)
(10)
Для получения аналитических
зависимостей для АЧХ и ФЧХ ВЭП по w
для управления произведем замену в (7): ![]()
W![]() ,
,
W![]() , W
, W
![]()
![]()
 ,
, ![]()
Для построения АЧХ и ФЧХ ВЭП использовались стандартные процедуры пакета MatLab 6.12
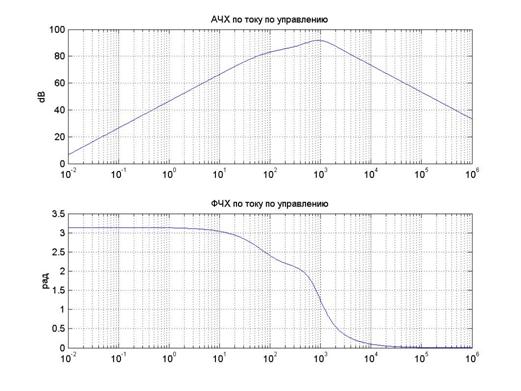
Рис 8. АЧХ и ФЧХ по току для управления.
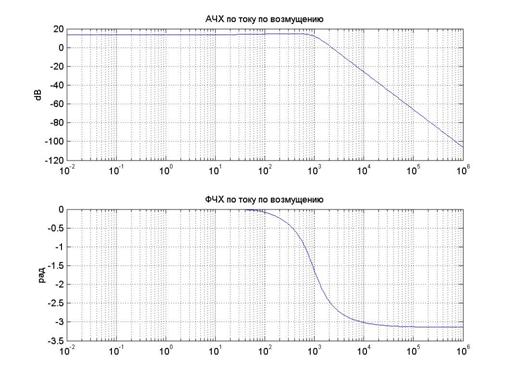
Рис 9. АЧХ и ФЧХ по току для возмущения.
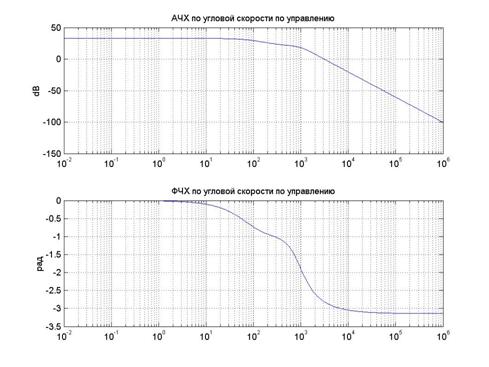
Рис 10. АЧХ и ФЧХ по угловой скорости для управления.
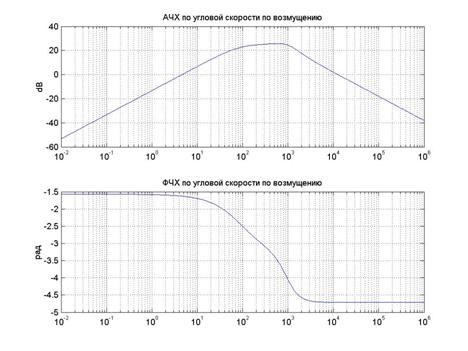
Рис 11. АЧХ и ФЧХ по угловой скорости для возмущения.
6. Расчет суммарного момента возмущения
Мв определяется по формуле:
![]() (26)
(26)
Полагаем ![]()
Реактивный момент представляется в виде ряда Фурье:
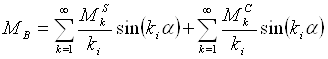 (27)
(27)
где
![]() и
и
![]() - амплитуды синусной и
косинусной составляющих в ряду Фурье.
- амплитуды синусной и
косинусной составляющих в ряду Фурье.
ki - номер гармоник разложения.
Суммарный момент выглядит следующим образом:
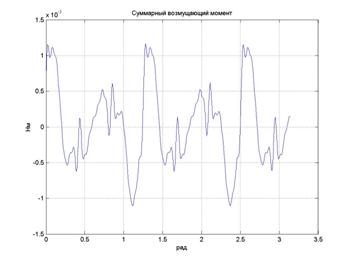
Рис 10. Суммарный момент возмущения.
Время динамического запаздывания (сек) из ФЧХ по току и угловой скорости для управления:
![]()
| Частота (Гц) | 0,1592 | 1,1273 | 2,0955 | 3,0637 | 4,0318 | 5,0000 |
| Время запаздывания по току | 3,1312 | 0,4331 | 0,2283 | 0,1530 | 0,1139 | 0,0901 |
| Время запаздывания по скорости | 0,0104 | 0,0104 | 0,0103 | 0,0102 | 0,0101 | 0,0099 |
Заключение
В курсовой работе была проанализирована математическая модель вентильного электропривода, построены частотные графики модели (по току и по W), а так же графики переходных процессов при различных программных напряжениях. На основании вида этих графиков, а также проведенного расчета устойчивости можно сделать вывод о устойчивости вентильного электропривода (его математической модели).