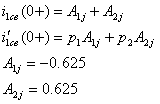Контрольная работа: Расчет переходных процессов в линейных электрических цепях
Министерство образования и науки Украины
Донбасская государственная машиностроительная академия
Кафедра электротехники и электрооборудования
Расчетно-графическая работа
Расчет переходных процессов в линейных электрических цепях
Выполнил:
Проверил:
Краматорск
Задание
В заданных вариантах необходимо: для каждой цепи рассчитать токи и напряжения во время переходного процесса вызванного коммутацией - определить их аналитические выражения и построить временные графики i (t), u (t). Задачи решить классическим и операторным методами.
Задача №1
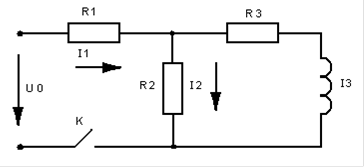
U0=1000 В
R1=120 Ом
R2=50 Ом
R3=10 Ом
L=0.4 Гн
Рис. 1.
Решение задачи классическим методом
Составим уравнения по 1-му и 2-му законам Кирхгофа в дифференциальной форме для послекоммутационного режима.
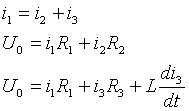
Составленную систему уравнений называют математической моделью динамического режима работы цепи.
Токи и напряжения до коммутации:
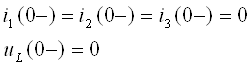
Принужденные составляющие токов и напряжения
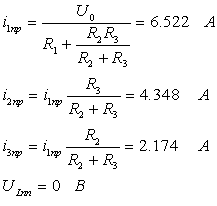
Определим полные значения токов и напряжений в первый момент после коммутации. На основании первого закона коммутации:
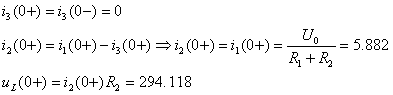
Свободные составляющие токов и напряжений в первый момент после коммутации.
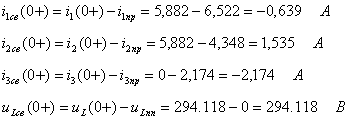
Составляем характеристическое уравнение и определяем показатель затухания:
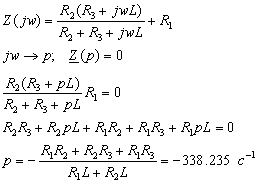
Постоянная времени переходного процесса
![]()
7. Выражения для свободных токов и напряжений:
![]()
8. Определяем постоянные интегрирования:

9. Свободные токи и напряжения:
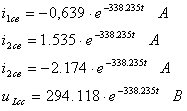
10. Полные токи и напряжения во время переходного процесса
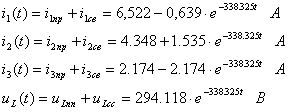
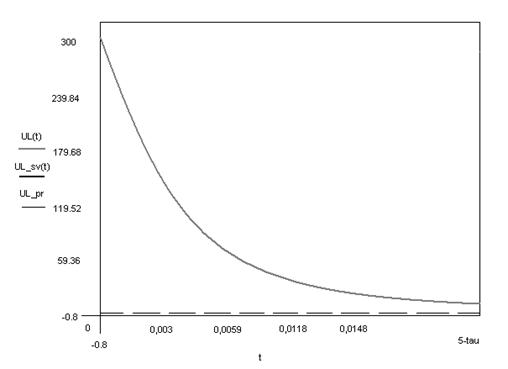
11. Построим графики токов и напряжений во время переходного процесса:
График тока i1
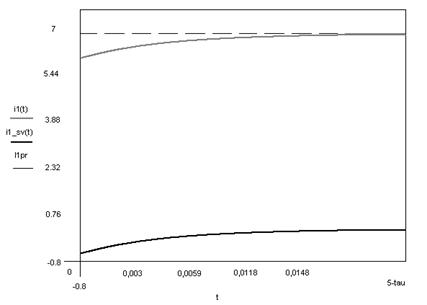
График тока i2
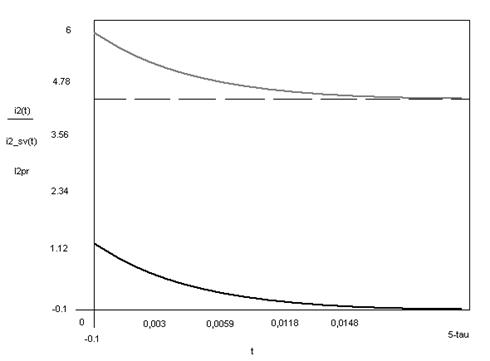
График тока i3
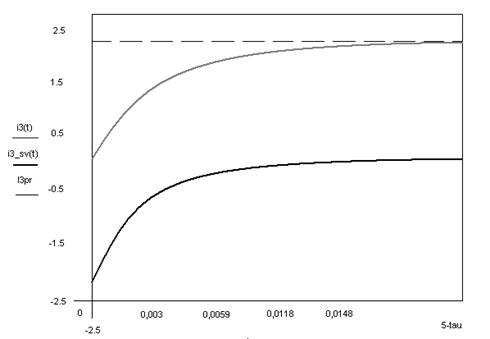
График напряжения на индуктивности ul
Решение задачи операторным методом
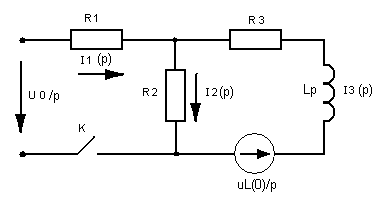
Рис.2.
Представим схему замещения цепи в операторной форме (рис.2) для после коммутационного режима.
Для расчета токов и напряжения U1в операторной форме используем метод непосредственного применения законов Кирхгофа. Составим уравнения по 1-му и 2-му законам Кирхгофа в операторной форме:

Так как напряжение на
индуктивности до коммутации было равно нулю, внутренняя ЭДС ![]() также равна нулю, в
дальнейших расчетах ее не учитываем.
также равна нулю, в
дальнейших расчетах ее не учитываем.
Из второго уравнения:

Из третьего уравнения:

Значения I2 (р) и I3 (р) подставим в первое уравнение:
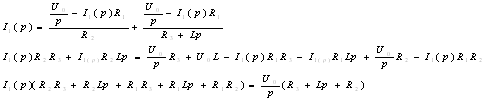
Выражение для тока первой ветви в операторной форме:
![]()
![]()
Выражение для I1 (р) получено в виде дроби, числитель и знаменатель которой полиномы.
![]()
N (p) =150000 + 400р – полином числителя, где
М (р) = 23000р + 68p2 - полином знаменателя
Определяем корни полинома знаменателя:
23000p + 68 p2 = p (23000 + 68 p)
p1=0;
p2=![]()
Для перевода тока I2 (р) из области изображений в область временных функций применяем формулу
![]()
где N (р1) и N (р2) - соответственно значения полиномов числителя при корнях р1 и р2 М' (р1) и М' (р2) - значения производной от полинома знаменателя соответственно при корнях р1 и р2. Полиномы числителя при корнях р1 и р2:
N (р1) = 150000; N (р2) = 14706
Производная от полинома знаменателя:
М (р) = 23000 + 136p
Производная от полинома знаменателя при корнях р1 и р2.
м' (р1) = 23000; М' (р2) = - 23000;
Ток i1 во время переходного процесса:
![]()
Остальные токи и напряжения определим используя законы Ома и Кирхгофа
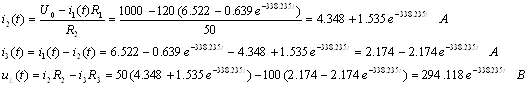
При расчете операторным методом получены те же выражения для токов и напряжения как и при расчете классическим методом, что подтверждает правильность выполненного расчета переходного процесса.
Задача №2
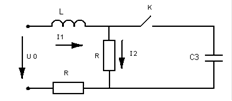
U0=160 B
R=80 Oм
L=0.8 Гн
С=20*10-6 Ф
Рис 3.
Необходимо найти закон изменения токов во всех ветвях и напряжений UL и UC в зависимости от времени и построить графики.
Решение задачи классическим методом
Математическая модель динамического режима работы цепи для послекоммутационного режима:
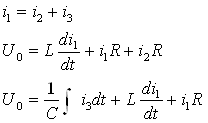
Решая данную систему дифференциальных уравнений, можно получить закон изменения токов и напряжений во времени в момент переходного процесса, не используя специальных методов. Доя упрощения решения системы воспользуемся классическим методом.
1. Токи и напряжения до коммутации.
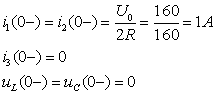
2. Принужденные значения токов и напряжений
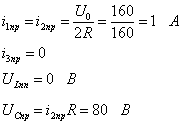
3. Полные значения токов и
напряжений в первый момент после коммутации: ![]()
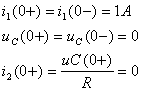
![]()
3. Свободные значения токов и напряжений в первый момент после коммутации:
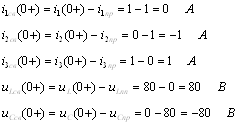
Определим производные свободных токов и напряжений в момент времени непосредственно после коммутации, для чего составим систему уравнений, используя законы Кирхгофа.
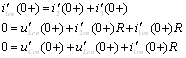
Производные от тока на индуктивности и напряжения на емкости:

Отсюда
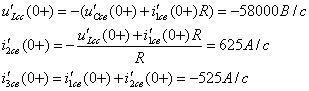
Все полученные результаты занесем в таблицу:
|
i1 |
i2 |
i3 |
UL |
uс |
|
|
t = 0 + |
1 |
0 |
1 |
80 |
0 |
| t=∞ |
1 |
1 |
0 |
0 |
80 |
|
Iсв (0+) |
0 |
-1 |
1 |
||
|
Uсв (0+) |
80 |
-80 |
|||
|
I’св (0+) |
100 |
625 |
|||
|
U’св (0+) |
-58000 |
50000 |
Составим характеристическое уравнение (для послекоммутационного режима) и определим его корни:
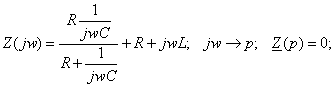
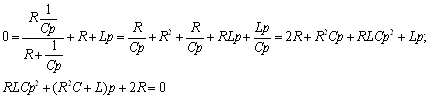
Подставим численные значения параметров цепи:
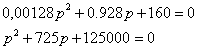
Решив квадратное уравнение получаем:
р1 = - 282.461
р2 = - 442.539
7. Определим постоянные интегрирования А1 и А2, и запишем выражения для токов и напряжений а) Для тока i1св: