Курсовая работа: Расчет трансформатора двухтактных преобразовательных устройств
Тольяттинский политехнический институт
Кафедра «Промышленная электроника»
Пояснительная записка
к курсовой работе
по дисциплине «Магнитные элементы электронных устройств»
Расчет трансформатора двухтактных преобразовательных устройств
Студент:
Моторин С.К.
Группа:
Э-206
Преподаватель:
Слукин А.М.
Тольятти 2002
Содержание.
1. Исходные данные для расчета
1.2. Исходные Данные уточняемые в процессе расчета
2. Оценочный расчет
2.1. Выбор материала сердечника
2.2. Определение типоразмера сердечника
2.3. Определение массы и объёма трансформатора
3. Конструктивный расчет
Выводы
Список используемой литературы
Исходные данные к расчёту.
1.1. Основные исходные данные:
совокупность чисел, характеризующих фазность обмоток:
m1=2, m2=3;
напряжение, подключённое к вторичной обмотке:
U21=30 В; U22=5; U23= 12
мощность:
P2=10 Вт;
электродвижущая сила (ЭДС) прикладываемая к первичной обмотке:
E1=600 B;
частота коммутаций силовых ключей:
f=30 кГц;
температура окружающей среды:
То=40 оС;
максимально допустимая относительная величина тока намагничивания:
Im max<=0.2;
максимально допустимая температура наиболее нагретой точки трансформатора;
Tт max=130 оС;
коэффициент теплоотдачи:
a=1.2×10-3 Вт/(см2 К);
коэффициент полезного действия (КПД):
h=0.9.
максимальный коэффициент заполнения окна сердечника обмотки:
l0 max=0.7;
1.2 Исходные данные, уточняемые в процессе расчета:
Коэффициент заполнения сечения обмотки проводниковым материалом(п):
0.5 £п (ПЭЛ)
п 0.65 (ПЭЛШО)
Простейшая схема преобразователя (рис.1.1.) состоит из трансформатора Т с двумя секциями первичной обмотки, ключей S1 и S2, поочерёдно замыкающих цепь постоянного тока с определённой частотой, сопротивления нагрузки Rн, подключенного к вторичной обмотке.
Расчёт ориентирован преимущественно на проектирование трансформаторов тороидальной конструкции (рис.1.2.) и состоит из двух частей: оценочного и конструктивного.
2. Оценочный расчёт.
2.1. Выбор материала сердечника:
Целью оценочного расчета является определение основных параметров трансформатора, выполненного на кольцевом сердечнике разных типоразмеров их стандартного ряда.
Для работы на частоте от 10 кГц и выше в качестве материала сердечника применяются ферриты 2000НМ-1, 1500НМ-1 и др. Выбирали марку сердечника. Для этого построили зависимости удельных потерь мощности в сердечнике от перепада индукции DВ в нём:
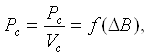 (2.1.)
(2.1.)
Где Рс - потери мощности в сердечнике, Вт;
Vc - объём сердечника, м3.
Использовали выражение:
Схема простейшего преобразователя напряжения.
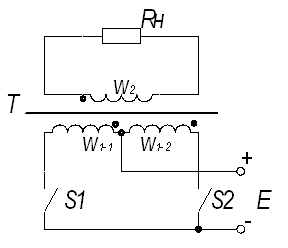
Рис. 1.1.
Трансформатор тороидальной конструкции.
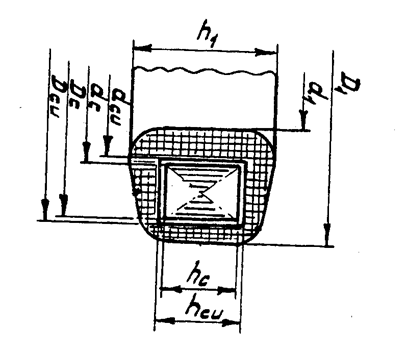
Рис. 1.2.
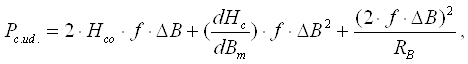 (2.2.)
(2.2.)
где f - заданная частота, кГц;
DВ - изменение магнитной индукции в сердечнике трансформатора за ту
часть периода Т/2, когда это изменение происходило в одном направлении, Тл;
Hco, dHc/dBm, Rв – величины найденные по таблице 2.1 [1].
По формуле (2.2.) рассчитали для каждого материала зависимость Рс.уд. от DВ в виде таблицы, задаваясь последовательно значениями:
![]()
где N – целое число;
х = 0,1..0,2;
Bm – амплитудное значение магнитной индукции, Тл [1, табл.2.1].
Данные для расчета взяли из таблицы 2.1:
Таблица 2.1.
Параметры аппроксимирующих выражений, описывающих магнитные свойства ряда ферримагнетиков.
|
№ пп |
Тип фер. | B, Тл |
|
|||||||||||||||
|
Hco, A/m |
dHc/dBm A/(m×Тл) |
DH0/dBm, A/(m×Тл) |
H0, A/mH0, A/m |
Bm2, Тл |
b |
RВ коМ/м |
|
|||||||||||
|
1. | 6000НМ | 6.4 | 0 | 48.3 | 776 | 0.355 | 15 | 4.4 | |||||||||
| 2. | 4000НМ | 1.06 | 8 | 80 | 758 | 0.38 | 16 | 26 |
|
|||||||||
| 3. | 3000НМ | 3.68 | 16 | 94.4 | 755 | 0.37 | 20 | 31 |
|
|||||||||
| 4. | 2000НМ | 1.2 | 40 | 164 | 719 | 0.39 | 12 | 56 |
|
|||||||||
| 5. | 2000НМ1 | 7.2 | 40 | 160 | 725 | 0.34 | 7 | 63 |
|
|||||||||
| 6. | 1500НМ2 | 0 | 65.4 | 240 | 699 | 0.33 | 10 | 180 |
|
|||||||||
| 7. | 1500НМ3 | 6.77 | 37 | 212 | 699 | 0.38 | 10 | 180 |
|
|||||||||
| 8. | 1000НМ3 | 20 | 0 | 250 | 715 | 0.258 | 10 | 280 |
|
|||||||||
| 9. | 700НМ | 0 | 75.4 | 844 | 749 | 0.4 | 2 | 1000 |
|
|||||||||
Для материала 6000НМ:
Hco = 6.4 А/м,
dHc/dBm = 0 А/(м×Тл),
Rв = 4,4 кОм/м.
x = 0.15
Подставляя числовые значения в (2.1.) получилипри В = 0 Тл
Рс.уд.=0 Вт/м3
при В=0,1 Тл
![]()
Рс.уд.= 38,4 Вт/м3,
при В=0,2 Тл
![]()
Рс.уд.= 76,8 Вт/м3, и т.д.
Аналогично рассчитали зависимости Рс.уд.(В) для других материалов Результаты вычислений занесли в табл.2.1.
Таблица 2.1.
Рассчитанные значения Рс.уд., Вт/м3.
| Тип фер. | B, Тл | |||||||
| 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 | |
| 6000НМ | 0 | 38,4 | 76,8 | 115,2 | 153,7 | 192,2 | 230,7 | 269,2 |
| 4000НМ | 0 | 8,7 | 22,3 | 40,7 | 63,8 | 91,8 | 124,6 | 162,2 |
| 3000НМ | 0 | 26,8 | 63,3 | 109,4 | 165,1 | 230,4 | 305,3 | 389,8 |
| 2000НМ | 0 | 19,2 | 62,4 | 129,6 | 220,8 | 336,1 | 475,2 | 638,4 |
| 2000НМ1 | 0 | 55,2 | 134,4 | 237,6 | 164,8 | 516,1 | 691,2 | 890,4 |
| 1500НМ2 | 0 | 19,6 | 78,5 | 176,6 | 313,9 | 490,5 | 706,3 | 961,3 |
| 1500НМ3 | 0 | 51,7 | 125,6 | 221,7 | 340,1 | 480,6 | 643,3 | 828,2 |
| 1000НМ3 | 0 | 120 | 240 | 360 | 480 | 600 | 720 | 840 |
| 700НМ | 0 | 22,6 | 90,5 | 203,6 | 361,9 | 565,5 | 814,3 | 1108,4 |
По данным таблицы 2.1. построили графики (рис. 2.1.).
Анализируя график, увидели, что наименьшими удельными потерями в заданных условиях обладает материал 4000НМ. Следовательно, выбрали для нашего сердечника материал 4000НМ.
2.2 Определение типоразмера сердечника
Определили типоразмер, начиная с которого в стандартном ряде (таб.2.2) сердечники пригодны для изготовления трансформатора с заданными исходными параметрами.
2.2.1 Приняли:
l0 =l0макс=0,7.
2.2.2 Из стандартного ряда (табл. 2.2, [1]);
Таблица 2.2.
Данные для расчета трансформаторов, выполненных на сердечниках различного размера из стандартного ряда при l0= 0.7.
|
№ сердеч. |
Тип сердечника |
Pp*, Вт/(Тл*кГц)2 |
Sт, см2 |
Vт, см3 |
Мт, г |
| 1. | К12х8х3 | 4.71 | 4.71 | 0.98 | 5.3 |
| 2. | К28х16х9 | 582.3 | 25.6 | 12.28 | 45.2 |
произвольно выбрав сердечник с размерами Dc´dc´hc и определили для него предельную мощность потерь PТмакс и объем Vc по формулам
![]() (2.3.)
(2.3.)
где a=1.2×10-3 Вт/(см2 К) - коэффициент теплоотдачи;
Sт - площадь поверхности охлаждения трансформатора, см2 (табл.2.2),
и
![]() (2.4.)
(2.4.)
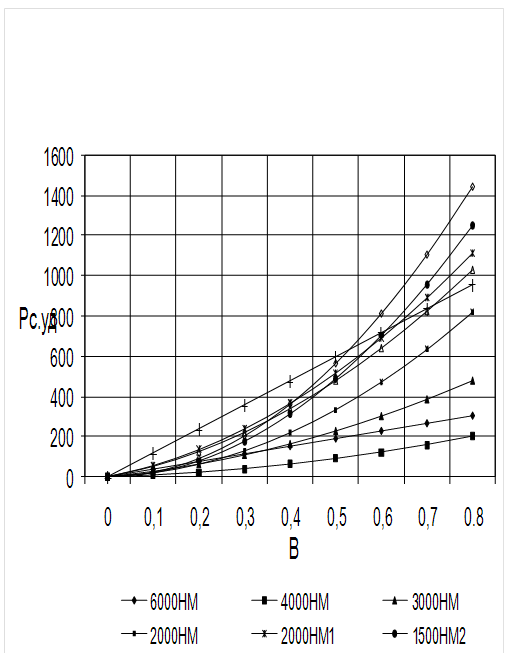
Зависимость удельных потерь мощности Рс.уд. от изменения магнитной индукции в сердечнике B.
|
Sт = 4,71 см2,
PТмакс= 3,14×1,2×10-3/(1.4× (130 -40) ×4,71) = 1,597
PТмакс = 1,597 Вт,
Vc = 3,14/(4×(82-32) ×12)
Vc = 0,000188 м3.
2.2.3. Для выбранного сердечника определили оптимальный режим перемагничивания:
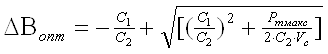 , (2.5.)
, (2.5.)
где
![]() ;
;
![]() .
.
C1=30000×1,06=31800
C2=30000×8+(2×30000)2/26000=378461
DBопт=-31800/378461+[(31800/378461)2 +1,597/(2×378461×0,000188)]0.5=1,76
Получили DBопт =1,76 Тл. т.к. DBопт > Bmax то за величину DBопт приняли Bmax=2×Вm2:
DBопт=0.76 Тл;
2.2.4. Для найденных значений DBопт определили амплитудное значение напряженности магнитного поля Hm при DBопт:
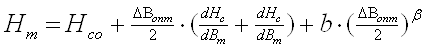 , (2.6.)
, (2.6.)
где dHo/dBm , b взяты из таблицы 2.1, b=3.849×109.
Для выбранного сердечника
Hm = 1,06 + (0,76/2) × (8+80) + 3.849×109× (0,76 /2)16
Hm = 762,1 А/м.
2.2.5 Определили относительную величину амплитуды тока намагничивания
по формуле, в которую поставляли DB=DBопт и Hm, вычисленное ранее по выражению (2.5.) при DBопт:
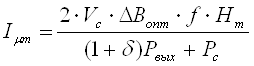 , (2.7.)
, (2.7.)
Где Pвых - мощность, Вт, которая может быть передана в нагрузки на вторичной стороне при числе вторичных обмоток n³2:
Pвых=åPn
где Pn - мощность, Вт, передаваемая через каждую из вторичных обмоток, из исходных данных;
d - отношение потерь мощности в каждой из обмоток Pwn к мощности Pn, передаваемой через нёё;
Величину d определили по выражению:
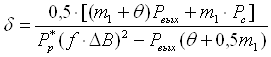 , (2.8.)
, (2.8.)
где m1,m2 - фазность, соответственно, первичной и вторичной обмоток. Для вторичных обмоток учитывается в виде:
q=åmn×Pn/Рвых=3;
Рс - потери в сердечнике, Вт, определяемые через удельные потери по формуле (2.1) и для выбранного сердечника равны - 0,0352Вт;
P*p - приведенная расчётная мощность сердечника, из таблицы 2.2 с учетом поправки на 130 оС:
P*p= 4,71 / (1+0.004×(130оС-40оС)) = 3,46 (Вт). (2.9.)
Подставляя числовые значения, получили
d = 0.5×((3+1)×100+3×0,352)/3,46×(30000×0,76)2-10·(3+0.5×3), (2.8.)
d=0,0021.
Таким образом, величина тока намагничивания
м=2×0,000188×0,76×30000× 799,88/(1+0,021) ×10 +0,352
Imм =0.651.
2.2.6 Вычислили максимальную выходную мощность трансформатора, выполненного на выбранном сердечнике:
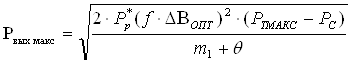 , (2.10.)
, (2.10.)
Pвых макс=[2× 3,46× (30000×0,76)2× ( 1,597-0,352)/(3+3)]0.5 = 10.247 Вт.
2.2.7 По таблице 2.2 определили объём трансформатора, соответствующий вычисленному значению максимальной мощности, т.е. VТ (Pвых.макс)
Vт=1,15см3.
Аналогично проводится расчет и для других сердечников. Вычислили значения Pвых.макс и VТ для типоразмера для К28´16´9:
Pвых.макс =1540,71 Вт,
Vт=12,28см3.
2.2.8 Построили зависимость
Vт(Pвых.макс). По графику этой зависимости определили ориентировочный объём трансформатора, для которого Pвых.макс = 10 Вт (рис. 2.2.). Получили ориентировочный объём равный:
Vт = 0,9 см3.
![]()
2.2.9. По таблице 2.2 выбрали
типоразмеры сердечников, для которых при lо=l0макс=0,7 трансформаторы имеют объём, отличающийся от найденного
в значениях на +20...40%: 2К10´6´3, К12´8´3, К12´5´5.5.
2.3. Для выбранных в пункте 2.2.9. сердечников определим минимальный размер массу трансформатора с заданными исходными параметрами. С этой целью для каждого из выбранных сердечников при нескольких значениях lо (0.7; 0.5; 0.3; 0.1) проведем следующие операции.
2.3.1. По уравнению (2.3.) определим Рт.макс(0). Величина Sт(0), необходимая для расчета, находится по таблице 2.2.
Рис. 2.2.
Зависимость объема трансформатора от мощности потерь в трансформаторе.
|
|
||||
При 0=0,1
PТмакс=3,14´1,2´10-3/1.4´(130-40)´4,71=0,7498
Для других 0 расчет аналогичен. Данные расчета занесены в таблицу 3.1.
Таблица 3.1.
Зависимость максимальной мощности потерь трансформатора от 0 , мВт
| l | Типоразмер сердечника | ||
| 2К10´6´3 | К12´8´3 | К12´5´5.5 | |
| 0.1 | 749.8 | 658 | 986.4 |
| 0.2 | 848.2 | 816.7 | 1054.2 |
| 0.3 | 947.6 | 979.1 | 1119.7 |
| 0.4 | 1047 | 1148.7 | 1187.5 |
2.3.2. По вычисленной таблице Рс.уд.(В) данного сердечника объемом Vc нашли зависимость Рс(В) c учетом выражения (2.1.)
2.3.3. С использованием уравнения:
![]() , (2.11.)
, (2.11.)
где Рт - мощность потерь в трансформаторе, Вт, а также уравнений (2.8.) и (2.1.), находя по таблице 2.2 значения Р*р с учётом поправки (2.9.), вычислим зависимость Рт(DВ) (табл.2.4.-2.6.).
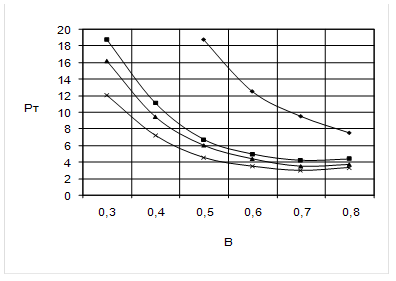
Таблица 2.4.
Рт для сердечника 2К10´6´3, Вт
| | B, Тл | |||||
| 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | |
| | - | - | 18.75 | 12.50 | 9.50 | 7.50 |
| | 18.75 | 10.50 | 6.75 | 5.00 | 4.00 | 3.75 |
| | 16.25 | 9.51 | 6.05 | 4.43 | 3.53 | 3.36 |
| | 12.05 | 7.22 | 4.55 | 3.50 | 3.00 | 3.00 |
Таблица 2.5.
Рт для сердечника К12´8´3, Вт.
| | B, Тл | ||||||
| 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
| | - | - | 17.00 | 11.00 | 7.00 | 5.00 | 4.75 |
| | - | 11.00 | 5.00 | 3.50 | 2.32 | 1.87 | 1.75 |
| | 15.70 | 6.50 | 3.50 | 2.00 | 1.31 | 1.25 | 1.25 |
| | 10.50 | 5.00 | 2.20 | 1.14 | 0.75 | 0.75 | 1.00 |
Таблица 2.6.
Рт для сердечника К12´5´5.5, Вт.
| | B, Тл | ||||||
| 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | |
| | - | - | 10.00 | 5.50 | 4.30 | 3.35 | 3.00 |
| | 15.00 | 6.25 | 3.25 | 2.00 | 1.27 | 1.00 | 1.00 |
| | 9.75 | 3.94 | 2.00 | 1.00 | 0.75 | 0.67 | 0.75 |
| | 6.25 | 2.75 | 1.00 | 0.52 | 0.38 | 0.43 | 0.51 |
Графики этих зависимостей представлены на рис. 2.3.-2.5.
Зависимость Рт от B для сердечника 2К10´6´3.
![]()
|
Зависимость Рт от B для сердечника К12´8´3.
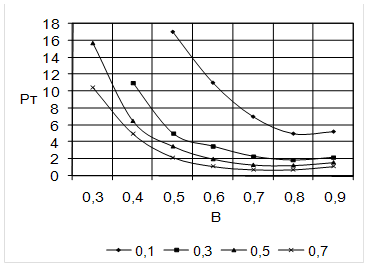
![]()
|
![]()
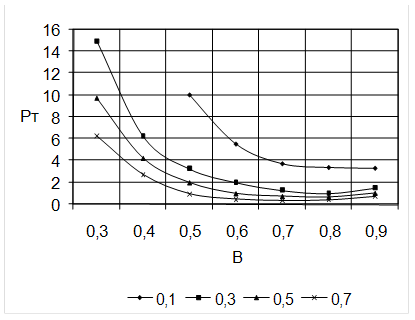
Рис. 2.5.
Зависимость Рт от B для сердечника К12´5´5.5.
2.3.4. По графикам (ри3.4. По графикам (рис. 2.3.-2.5.), при каждом значении 0, определили Ртопт - минимальную величину Рт. Если график имеет минимум при DВ>DВm, то за Ртопт приняли значение Рт соответствующее DВm. Найденные значения Ртопт и вычисленные в п.2.3.1. величины Рт.макс. заносли в таблицы 2.7.-2.9..
Таблица 2.7.
Сердечник 2К10´6´3 Рт, Вт.
|
|
||||
| 0,1 | 0,3 | 0,5 | 0,7 | |
| Рт.опт. | 9.80 | 4.20 | 3.80 | 3.00 |
| Рт.макс. | 0.75 | 0.85 | 0.95 | 1.05 |
Таблица 2.8.
Сердечник К12´8´3 Рт, Вт.
|
|
||||
| 0,1 | 0,3 | 0,5 | 0,7 | |
| Рт.опт. | 7.0 | 2.00 | 1.2 | 0.9 |
| Рт.макс. | 0.66 | 0.82 | 0.98 | 1.15 |
Таблица 2.9.
Сердечник К12´5´5.5 Рт, Вт.
|
|
||||
| 0,1 | 0,3 | 0,5 | 0,7 | |
| Рт.опт. | 3.5 | 1.50 | 0.8 | 0.60 |
| Рт.макс. | 0.99 | 1.05 | 1.12 | 1.2 |
На рис.2.6.- 2.8. представлены зависимости мощности потерь в оптимальном режиме и предельно допустимой мощности трансформатора от коэффициента заполнения окна сердечника обмотками. Пунктиром обозначена величина заданных потерь
Рт = Рвых.(1/ .
Рт = 70×(1/0,9 .
![]()
|
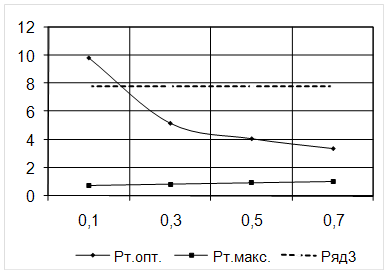
Зависимость мощности потерь в оптимальном режиме и предельно допустимой мощности трансформатора от коэффициента заполнения окна сердечника обмоткой для сердечника 2К10´6´3.
Зависимость мощности потерь в оптимальном режиме и предельно допустимой мощности трансформатора от коэффициента заполнения окна сердечника обмоткой для сердечника К12´8´3.
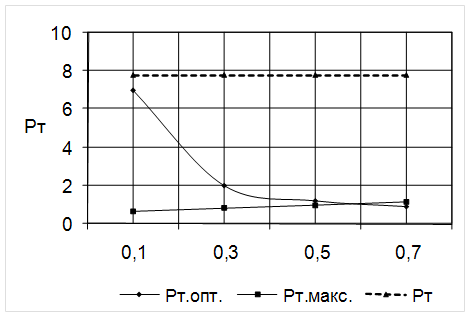
Рис.2.7.
Зависимость мощности потерь в оптимальном режиме и предельно допустимой мощности трансформатора от коэффициента заполнения окна
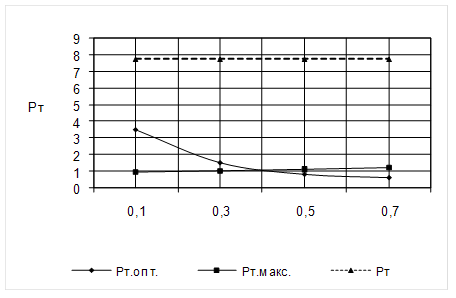
Рис. 2.8.
сердечника обмоткой для сердечника К12´5´5.5.
2.3.5. По полученным графикам определим величину мин, как абсциссу точки пересечения Рт.макс. и Рт.опт. Получили для типоразмера:
К12´8´3: мин =0.6.
К12´5´5.5: мин =0.4.
Для сердечника 2К10´6´3 значение мин очень велико, поэтому не принимали его во внимание. Из других двух типоразмеров выгоднее использовать К12´8´3, т.к. у него более высокий коэффициент заполнения окна обмоткой.
2.4. С использованием данных таблицы 2.2 построили зависимости Vт(lо) и Мт(lо) (рис.2.9, 2.10.). Из рисунка видно, что меньшим объемом и массой обладает сердечник К12´5´5.5. Следовательно, при заданных условиях использование этого сердечника является наиболее выгодным.
2.5 Для выбранного сердечника рассчитали величины B,
DBопт=-72000/497143+[(72000/497143)2+ +1,597/(2×497143×0,000188)]0.5=1,332
Т.к. DBопт > 2Bm поэтому за DB берется 2Bm.
B=0,780Тл,
d=0.5× ((2+1) ×70+2×0.74)/3,271× (60000×0,78)2-70 (1+0.5×2),
Вычислили значения плотностей тока для первичной и вторичной обмоток по формулам:
j1= d×2×DВ×f×S/q×lw , j2=d×2×DВ×f×S/((1+d)×q×lw.
где q- удельное электрическое сопротивление материала провода обмотки, равное 2.477*10-5 Ом×мм;
lw - средняя длинна витка обмотки, м:
![]()
S - сечение магнитопровода, м2:
S=0.5×hc(Dc-dc).
Получим:
lw=2×12+(5,52+0,4×52)0,5 - 5× (1-0,4) 0,5 = 26,4;
S=0.5×12(5,5-5)=3 см.
j1=1,71 А/мм2,
j2=1,73 А/мм2.
Зависимость объема трансформатора от коэффициента заполнения окна обмоткой.
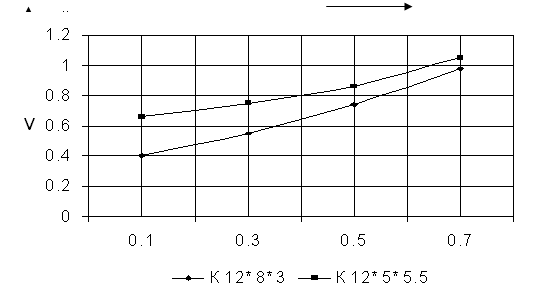 |
Рис. 2.9.
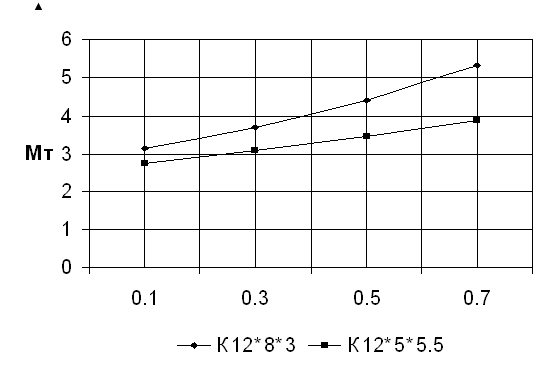 |
Зависимость массы трансформатора от коэффициента заполнения окна обмоткой.
3. Конструктивный расчет
3.1 Определим конструктивные данные первичной обмотки
3.1.1 Найдем число витков:
W1=E/(2(1+d)×DB×f×S)
W1=6/(2(1+0,0082) ×0,78×60000×3×10-6)=22
Сечение провода в первом приближении:
q1,1=Рвых /(hт×Е×j1)
q1,1=70 /(0,9×6×1,71)=0,076 (мм2).
3.1.2. По вычисленному значению q1,1
найдем по таблице П3[1] диаметр голого провода (без изоляции) dпр и с изоляцией dиз,, и по ним рассчитаем коэффициент заполнения. При рядовой намотке
lп1,1=Ку×(p/4)×(dпр/dиз)2=0,47
lп1,1=Ку×(p/4)×(dпр/dиз)2=0,47
3.1.3. По известным значениям найдем площадь окна сердечника, занятую первичной обмоткой
S1,1=m1×W1×q1,1/lп1,1=7,12 (мм2),
коэффициент заполнения окна сердечника обмоткой
lо1,1=4S1,1/p×dcu2
где dcu - внутренний диаметр изолированного кольцевого сердечника.
После изоляции размеры сердечника:
dcu=dc-2×Dв
Dcu=Dc+2×Dн
hcu=hc+Dв+Dн
где Dв и Dн - толщины изоляции по внутреннему и наружному диаметрам кольцевого сердечника, мм (приняты равными 0,1мм).
Поэтому
lо1,1=0.39.
3.1.4 Найдем среднюю длину витка первичной обмотки:
lw1,1=2×hcu+ÖDcu2+lo1,1×dcu2-dcuÖ1-lo1,1 =28 (мм).
3.1.5 Определим во втором приближении сечение провода первичной обмотки:
q1,2=rt×W1× lw1,1(1+d)2× ((1+d)Pвых+Pc)/(d ×E2) =0,193 (мм2).
3.1.6 Точность наших вычислений определяется следующим образом:
2(q1,2- q1,1)/( q1,2+ q1,1)=0.06
Эта величина достаточно мала, чтобы остановить расчет на значении
q1=0.076 мм2.
3.1.7 Определим размеры эквивалентного тороидального сердечника после намотки на него первичной обмотки:
внешний диаметр:
D1=ÖDcu2+lo1,1×dcu2 =6,44 (мм).
внутренний диаметр:
d1=dcuÖ1-lo1,1 =3,75 (мм).
высота:
h1=hcu+0.5(dcu(1-Ö1-lo1,1)+ ÖDcu2+lo1,1×dcu2-Dcu)=13,1 (мм).
3.2 Определим конструктивные данные вторичной обмотки.
3.2.1 Найдем число витков:
W2=U2× (1+d)/2DB×S×f = 862,
сечение провода в первом приближении:
q2,1=P2/U2×j2=0.0017 (мм2).
3.2.2. По величине q1,2 и таб.П3 определим диаметры провода dпр (активное сечение) и dиз, а по ним величину коэффициента lп2,1 по аналогично п.3.1.2.
lп2,1=0.245.
3.2.3 В первом приближении найдем площадь занятую вторичной обмоткой:
S2,1=m2×W2×q2,1/lп2,1=5,98 (мм2),
коэффициент:
l02,1=4S2,1/p×d12=0,54.
среднюю длину витка вторичной обмотки:
lw2,1=2×h1+ÖD12+lo2,1×d12-d1Ö1-lo2,1=30,6 (мм).
и во втором приближении сечение провода вторичной обмотки:
q2,2=rt×W1×lw2,1×P2/d×U22 =0,002 (мм2).
3.2.4. Делаем проверку:
(q2,2- q2,1)/(q2,2+ q2,1)=0.081.
т.е. результат получен с достаточно высокой точностью.
3.2.5 Определим размеры эквивалентного тороидального сердечника, образовавшегося после намотки на него обмоток первичной и вторичной:
внешний диаметр:
D2=ÖD12+lo2,1×d12=7,00 (мм);
внутренний диаметр:
d2= d1Ö1-lo2,1 =2,54 (мм);
высота:
h0 (мм);
внутренний диаметр:
d2= d1Ö1-lo2,1 =2,54 (мм);
высота:
h2=h1+0.5(d1(1-Ö1-lo2,1)+ ÖD12+lo2,1×d12-D1)=14 (мм).
Вывод
В результате выполнения работы рассчитали трансформатор двухтактного преобразовательного устройства. Расчет вели по методу описанному в методичке [1]. На основании первых расчетов был выбран материал сердечника, удовлетворяющий условиям расчета и предельно-допустимым эксплутационным значениям. При выборе сердечника учитывали максимально-допустимую температуру окружающей среды. Так как в задании не сказано на какой нагрузке будет работать трансформатор, необходимо было брать тот сердечник, который проходил по температурным параметрам с запасом.
Произвели выбор типоразмера, на котором будет изготавливаться трансформатор, который должен отвечать следующим требованиям:
а) должен иметь минимальную массу и объем,
б) в нем должно быть как можно меньше активных потерь, иначе будет происходить нагрев трансформатора.
Исходя из этих условий выбрали типоразмер К12´5´5.5 объёмом V=0.8 см3 и массой М=4.1 г.
Произведя конструктивный расчет рассчитали число витков в первичной и вторичной обмотках, а также оптимальный коэффициент заполнения окна сердечника. Выполненные проверки подтверждают правильность сделанного расчета.
Литература
1. Методические указания к выполнению курсового проекта “Расчет трансформатора двухтактных преобразовательных устройств”. СлукинА.М.,1994г.
2. Ферриты и магнитодиелектрики: Справочник Общ. ред. Н.Д. Горбунов, Г.А.Матвеев. М.: Сов. радио, 1972. 239с.
3. Бальян Р.Х. Трансформаторы для радио электроники. – М.: Сов. радио, 1971. 720с.