Контрольная работа: Расчет электрической цепи постоянного тока
Задание на выполнение работы
Схема исследуемой цепи:
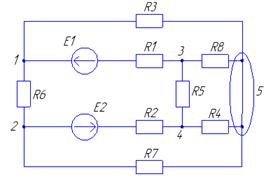
Рис. 1. Принципиальная схема исследуемой цепи
Таблица 1. Параметры элементов схемы
| Элемент схемы |
E1 |
E2 |
R1 |
R2 |
R3 |
R4 |
R5 |
R6 |
R7 |
R8 |
| U, V | 20 | 47 | ||||||||
|
RF, W |
51 | 130 | 175 | 240 | 300 | 140 | 179 | 500 |
Пункт 1. Рассчитаем значения токов ветвей методом уравнений Кирхгофа. Для расчета используем схему, приведенную на рис. 1. Данная схема содержит 5 узлов, 8 ветвей, 2 источника ЭДС и не содержит источников тока. Подсчитаем количество уравнений системы, составленной по методу Кирхгофа.
Количество уравнений для первого закона равно:
![]()
где Nу – количество узлов рассматриваемой принципиальной схемы.
Количество уравнений для второго закона равно:
![]() ,
,
где Nв, NT – количество узлов и источников тока соответственно.
Подставив значения, получаем, что количество уравнений, составленных по первому закону равно 4, а по второму также 4. Приняв положительное направление обхода контуров и направления токов в ветвях, отметим это на схеме (рис. 2.).
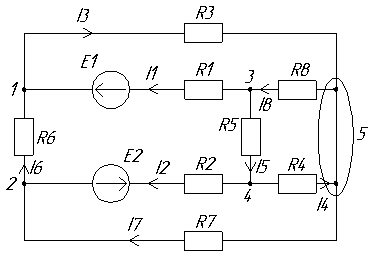
Рис. 2
Составим систему уравнений, основываясь на направлениях токов и положительном направлении обхода.

Подставив значения сопротивлений резисторов из таблицы 1, сформируем матричное уравнение вида A X = B, где

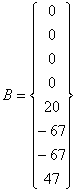
Решая указанную систему, получаем искомую матрицу Х, которая содержит значения токов.
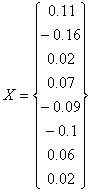
Найденные токи перечислены в таблице 2.
Таблица 2
| Номер тока | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Значение тока, mA | 11 | -16 | 2 | 7 | -9 | -10 | 6 | 2 |
Пункт 2. Рассчитаем токи в исходной схеме по методу контурных токов. Количество уравнений для данного метода равно количеству уравнений для второго закона Кирхгофа, которое было подсчитано ранее. Исследуемая принципиальная схема содержит 4 контура, в которых действуют 4 контурных тока, направления которых показаны на рис. 3.
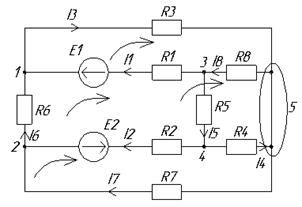
Рис. 3. Условные положительные направления контурных токов
Учитывая эти положительные направления можно записать систему уравнений по методу контурных токов в общем виде:
![]()
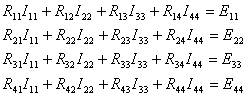
Собственные сопротивления контуров:
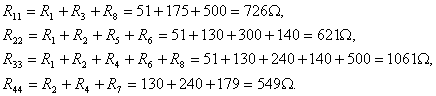
Общие сопротивления контуров:
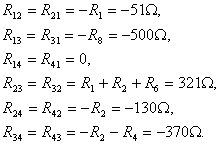
Контурные Э.Д.С.:
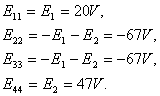
Матрицы, составленные по представленным данным имеют вид:
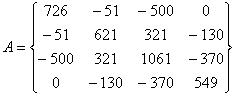
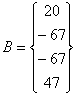
Решив систему, получим:
![]()
Зная контурные токи, находим токи в ветвях:
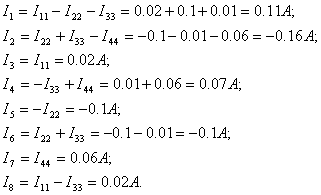
Сравнивая значения токов, полученные методом контурных токов и методом уравнения Кирхгофа, видим, что они практически совпадают.
Пункт 3. Рассчитаем токи методом узловых напряжений. Схема с нумерацией узлов и условными положительными направлениями узловых напряжений показана на рис. 4.
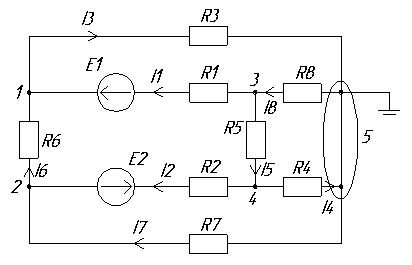
Рис. 4. Направления узловых напряжений.
Анализируемая схема содержит четыре независимых узла, значит количество уравнений будет равно количеству уравнения первого закона Кирхгофа, а общий вид системы для определения узловых напряжений будет таким:
![]()
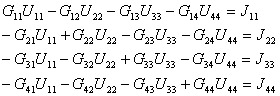
Собственные проводимости узлов:
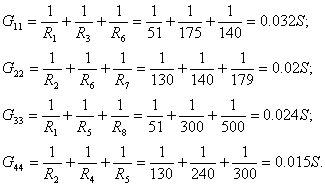
Общие проводимости узлов:
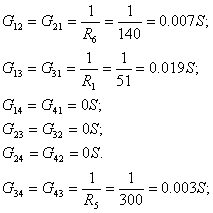
Узловые токи:
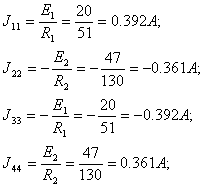
Матрицы имеют вид:
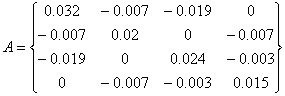
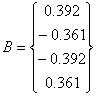
Решив систему, получим:
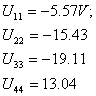
Зная узловые напряжения, найдем токи ветвей. Для этого воспользуемся вторым законом Кирхгофа:

Найденные токи совпадают с рассчитанными ранее другими методами.
Пункт 4. Преобразование заданной схемы в трёхконтурную.
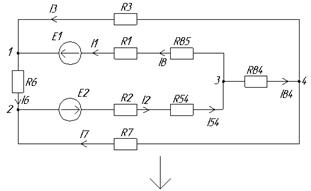
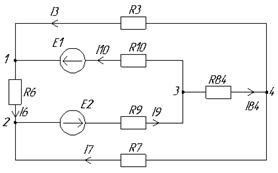
Рис. 5. Преобразование заданной схемы в трёхконтурную
Изменяются параллельно соединённые участки цепи одним эквивалентным.
![]()
![]()
![]()
Пункт 5. Рассчитаем токи в исходной схеме по методу контурных токов. Схема содержит три независимых контура с тремя контурными токами, она изображена на рис. 6.
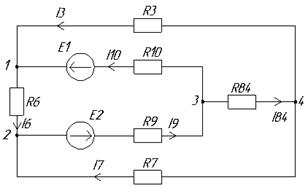
Рис. 6. Нахождение тока в преобразованной цепи
Необходимо составить систему уравнений для первого и второго уравнения Кирхгофа.
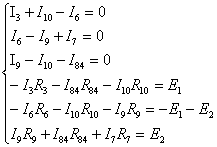
Составляем матрицу для получения нужных токов.

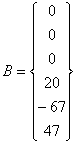
Получаем искомые токи:
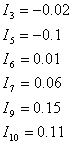
Пункт 6. Расчёт тока в заданной ветке методом эквивалентного генератора.
После разрыва исследуемой ветви схема примет вид, показанный на рис. 7.
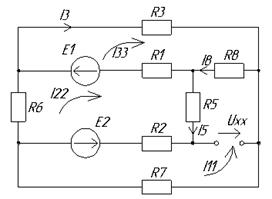
Рис. 7.
После разрыва
ветви ![]() схема упрощается:
резисторы
схема упрощается:
резисторы ![]() теперь образуют одну ветвь
с током
теперь образуют одну ветвь
с током ![]() .
.
Рассчитаем напряжение холостого хода, составив уравнение второго закона Кирхгофа:
![]() .
.
Для того,
чтобы рассчитать ![]() , необходимо
знать токи знать токи
, необходимо
знать токи знать токи ![]() и
и ![]() . После разрыва
. После разрыва ![]() схема содержит 3
независимых контура и 4 независимых узла. Поэтому рассчитаем токи методом
контурных токов. Система уравнений в общем виде будет такой:
схема содержит 3
независимых контура и 4 независимых узла. Поэтому рассчитаем токи методом
контурных токов. Система уравнений в общем виде будет такой:
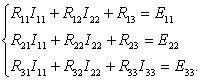
Собственные сопротивления контуров:
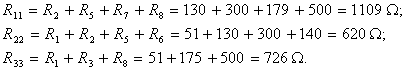
Общие проводимости узлов:
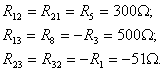
Узловые токи:
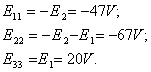
Матрицы имеют вид:
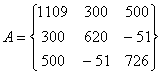 ,
, 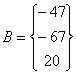
Ее решение: ![]() Искомые токи
Искомые токи ![]()
![]()
Теперь можно
найти![]() :
:
![]()
Для расчета ![]() исключим из схемы
источники энергии, оставив их внутренние сопротивления. Для этого имеющиеся в
схеме источники напряжения необходимо замкнуть накоротко. Схема без источников
имеет вид (рис. 8):
исключим из схемы
источники энергии, оставив их внутренние сопротивления. Для этого имеющиеся в
схеме источники напряжения необходимо замкнуть накоротко. Схема без источников
имеет вид (рис. 8):
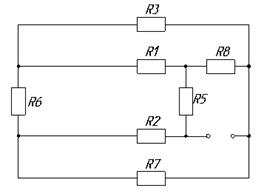
Рис. 8.
Схема для определения ![]()
В
принципиальной схеме резисторы ![]() ,
, ![]() и
и ![]() соединены треугольником.
Заменим это соединение эквивалентной звездой
соединены треугольником.
Заменим это соединение эквивалентной звездой ![]() ,
,
![]() ,
, ![]() . Имеем:
. Имеем:

![]()
После замены схема имеет вид (рис. 9):
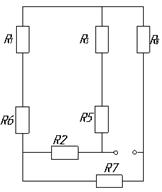
Рис. 9.
Проведём нужные преобразования ещё раз:
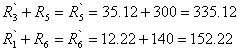
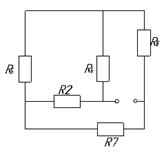
Рис. 10.
После
сделанных преобразований мы имеем еще один условный треугольник ![]() ,
,
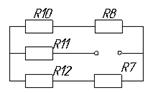
Рис. 11.

Эквивалентное сопротивление генератора можно найти следующим способом:
![]()
Для проверки
правильности расчетов определим по формуле эквивалентного генератора ток в
ветви с ![]() в исходной схеме:
в исходной схеме:
![]()
Этот ток практически совпадает с найденным ранее, что свидетельствует о буквальной правильности вычислений.
| Ток | Метод уравнений закона Кирхгофа | Метод контурных токов | Метод узловых напряжений | Метод уравнений Кирхгофа для преобразованной схемы | Метод эквивалентного генератора |
|
I1 |
0,11 | 0,11 | 0,11 | ||
|
I2 |
-0,16 | -0,16 | -0,12 | ||
|
I3 |
0,02 | 0,02 | 0,02 | -0,02 | |
|
I4 |
-0,07 | -0,07 | 0,07 | -0,1 | -0,07 |
|
I5 |
-0,1 | -0,1 | -0,1 | ||
|
I6 |
-0,01 | -0,01 | -0,01 | 0,01 | |
|
I7 |
0,06 | 0,06 | 0,06 | 0,06 | |
|
I8 |
0,02 | 0,02 | 0,02 | ||
|
I9 |
0,15 | ||||
|
I10 |
0,11 |