Контрольная работа: Решение задач по теоретической механике

Вариант 4

Задача 1

Дано:

Q=15 кН

G= 1,8кН

a=0,10м

b=0,40м

c=0,06м

f=0,25

Решение:

Рассмотрим по отдельности участки конструкции и приложенные к ним силы:

а) ΣX_S= X_D –T=0

б) ΣY_S= Y_D – Q=0

в) Σm_O( F_S)= T*R – Q*R=0

Из уравнения «в» находим T и Q:

T=Q=15 кН

X_D=T=15 кН

Y_D=15кН

2) а)ΣX_O= X_O +T+ F_ТР._max =0

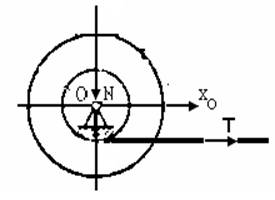
б)ΣY_O= Y_O – N-G=0

в)Σm_O( F_S)= T*R – F_ТР._max*2R=0 F_ТР._max

Из уравнения «в» находим силу трения

F_ТР._max=T/2=7,5кН

После чего находим нормальную реакцию N

F_ТР._max=f*N откуда:

N= F_ТР._max/ f = 7,5 / 0,25=30 кН

После чего находим X_O_иY_O:

X_O= 30 - 7,5=22,5 кН

Y_O= 30 + 1,8= 31,8 кН

3) а) ΣX_A= X_A –F_ТР._max =0

б) ΣY_A= Y_A – P_min +N=0

в) Σm_O( F_S)= -N*B + P_min(a+b) - F_ТР_.max *c=0

Из уравнения «а»: X_A=F_ТР._max=7,5 кН

Из уравнения «в» находим минимальное значение силы P:

P_min= (N * b + F_ТР_.max* c) / (a + b)= ( 30 * 0,4 + 7,5 * 0,06) / 0,5 = 24,9 кН

После чего из уравнения «б» находим Y_A:

Y_A= 24,9 -30 = - 5,1 кН

Ответ: P_min= 24,9 кН X_O= 22,5 кН

Y_A= - 5,1 кН Y_O= 31,8 кН

X_A=7,5 кН F_ТР._max=7,5 кН

N=30 кН

Задача 2

Даны уравнения движения точки в прямоугольных декартовых координатах.

x=4t+4

y=-4/(t+1)

t1=2

Траектория точки (рис.1) - часть параболы с вертикальной осью симметрии.

Определим положение точки на траектории в рассматриваемый момент времени.

При t = 1c x = 0м y = 4м (координата равна -4)

Определяем скорость и ускорение точки с помощью уравнений движения по их проекциям на оси декартовых координат:

Vx = x' = 2

Vy = y' = -8t

V=√(Vx2 + Vy2) = √(4 + 64t2) = 2√(1+16t2)

При t=1c: Vx=2 м/с

Vy = -8 м/с

V=8,246 м/с

Направляющие косинусы для скорости равны

Cos (V^x) = Vx/V = 2/8,246 = 0,2425

Cos (V^y) = Vy/v = -8/8,246 = 0,97

ax = x'' = 0

ay = -8 м/с2

a=√(ax2 + ay2)

a= |ay| = 8 м/с2

cos (a^x) = ax/a =0

cos (a^y) = ay/a =1

Вектор ускорения направлен параллельно оси oy (по оси oy) в отрицательную сторону.

Уравнения движения точки в полярных координатах

r=√(x2 + y2)

φ = arctg y/x

Получаем: r= √[(2t-2)2 + 16t4] = √[4t2 - 8t + 4 + 16t4 = 2√[t2 - 2t + 1 + 4t4

φ=arctg[-4t4/(2t-2)]

Вычислим величину радиальной составляющей скорости

Vr=dr/dr

Vr = (2t-2+16t3)/[√(t2 - 2t + 1 + 4t4]

При t=1 сек Vr=8 м/с

Знак плюс показывает, что радиальная составляющая скорости направлена по радиус-вектору точки М.

Вычислим величину трансверальной составляющей скорости.

Vp = rd(φ)/dt

dφ/dt = 1/[1 + 16t4/(2t-2)2] * [-8t(2t-2) + 4t22]/(2t-2)2 = (4t-2t)2/[(t-1)2 + 4t4]

Vp=[2(4t-2t2√(t2 - 2t + 1 + 4t4)]/[(t-1)2 + 4t4] = (8t-4t2)/√(t2 - 2t + 1 + 4t4)

При t=1 Vp = 2 м/с

Знак плюс показывает, что трансверальная составляющая скорости направлена в сторону увеличения угла φ.

Проверим правильность вычислений модуля скорости по формуле:

V = √(Vr2 + Vp2) = √(4+64) = 8,246 м/с

Определим величины касательного и нормального ускорений точки. При естественном способе задания движения величина касательного ускорения определяется по формуле

aт=dVt/dt = d[√(x'2 + y'2)] = (Vxax + Vyay)/V = 64t/[2√(1+16t2)]=32t/√(1+16t2)

При t=1 c aт=7,76 м/с2

Так как знаки скорости и касательного ускорения совпадают, точка движется ускоренно.

Нормальное ускорение:

an=√(a2 - a2т)

an = √(64-60,2176) = √3,7284 = 1,345 м/с2

Задача Д 8

Применение теоремы об изменении количества движения к исследованию движения механической системы.

Дано:

Найти: Скорость .

Решение:

На механическую систему действуют внешние силы: - сила сухого трения в опоре А; - силы тяжести тел 1, 2 и 3; -сила нормальной реакции в точке А; -реактивный момент в опоре В.

Применим теорему об изменении количества движения механической системы в дифференциальной форме. В проекциях на оси координат

, (1)

где - проекции вектора количества движения системы на оси координат; - суммы проекций внешних сил на соответствующие оси.

Количество движения системы тел 1, 2 и 3

(2)

где

. (3)

Здесь - скорости центров масс тел 1, 2, 3; - соответственно переносные и относительные скорости центров масс.

Очевидно, что

(4)

Проецируя обе части векторного равенства (2) на координатные оси, получаем с учетом (3) и (4)

(5)

где - проекция вектора на ось ;

Проекция главного вектора внешних сил на координатные оси

(6)

Знак « - » соответствует случаю, когда , а знак «+» - случаю, когда .

Подставляя (5) и (6) в (1), получим

(7)

Выразим из второго уравнения системы (7) величину нормальной реакции и подставим ее в первое уравнение. В результате получим

при ; (8)

при . (9)

где

Рассмотрим промежуток времени , в течении которого тело 1 движется вправо . Из (8) следует, что

где С- постоянная интегрирования, определяемая из начального условия: при

При скорость тела 1 обращается в ноль, поэтому .

Найдем значения и :

Т.е. , . Значит, тело при начинает двигаться в обратном направлении. Это движение описывается дифференциальным уравнением (9) при начальном условии: ; (10)

Интегрируя (9) с учетом (10), получим, при

(11)

При получим из (11) искомое значение скорости тела 1 в момент, когда

Точное решение задачи. Воспользовавшись методикой, изложенной выше, получим дифференциальное уравнение движения тела 1:

при (12)

; при , (13)

где

Из (12) и учитывая, что получаем, при

откуда или

Из (13) и учитывая, что получаем, при

При находим

Ответ: .

Задача Д 3

Исследование колебательного движения материальной точки.

Дано:

Найти: Уравнение движения

Решение:

Применим к решению задачи дифференциальное уравнение движения точки. Совместим начало координатной системы с положением покоя груза, соответствующим статической деформации пружины, при условии что точка В занимает свое среднее положение . Направим ось вниз вдоль наклонной плоскости. Движение груза определяется по следующему дифференциальному уравнению: